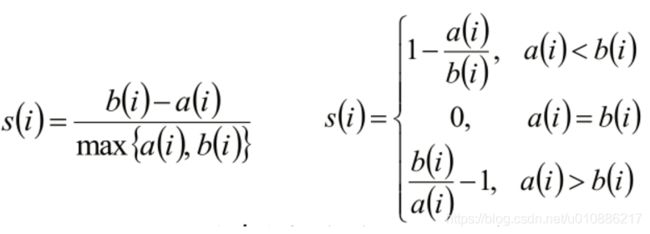机器学习（1）：K-MEANS聚类算法

一、聚类简介

1.无监督问题：我们手里没有标签了
2.聚类：相似的东西分到一组
3.难点：如何评估，如何调参

二、基本概念：

1.K：要得到簇的个数，需要指定K
2.质心：均值，即向量各维取平均
3.距离的度量：常用欧几里得距离和余弦相似度（先标准化）
4.优化目标

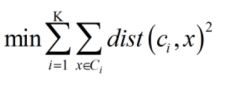
（1）Ci代表第i个簇的中心
（2）x是属于Ci的点
（3）dist：为distance距离，即欧几里得距离
（4）目标为：每一个点到该簇的距离之和，以及各个簇中心之和，为最小值！
5.注意：
（1）标准化
比如X轴0.01，0.02，0.03偏差比较小；Y轴，105，161偏差比较大。为了消除值本身大小的影响，所以需要将X/Y的范围都归类到[0,1]或者[-1,1]。
（2）一般用欧几里得距离

 

三、工作流程

1.初始化：假设K=3，即三个初始化点，C1,C2,C3。初始化三个点。

2.分类：然后，依据其他点与三个核心点距离来分类。

3.更新质心C1,C2,C3：依据2中的分类，求取每个分类的质心，作为新的C1',C2',C3。

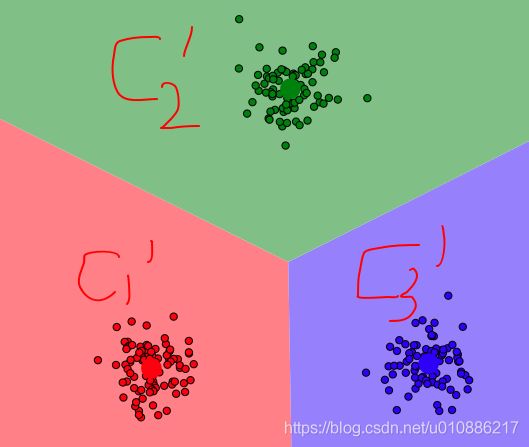
4.循环2到3
5.结束：当C1,C2,C3和C1',C2',C3'偏差满足要求停止。即，满足优化目标为止！

四、优势和劣势

1.优势
简单，快速，适合常规数据集
2.劣势
（1）K值难确定
（2）复杂度与样本呈线性关系
（3）很难发现任意形状的簇

五、聚类可视化

可视化网址过程【老外的网址，不错！】
（1）k-means
https://www.naftaliharris.com/blog/visualizing-k-means-clustering/
（2）dbscan
https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/

六、实例

针对数据data.txt

	name	calories	sodium	alcohol	cost
0	Budweiser	144	15	4.7	0.43
1	Schlitz	151	19	4.9	0.43
2	Lowenbrau	157	15	0.9	0.48
3	Kronenbourg	170	7	5.2	0.73
4	Heineken	152	11	5.0	0.77
5	Old_Milwaukee	145	23	4.6	0.28
6	Augsberger	175	24	5.5	0.40

1.python代码实现

1.获取数据
# beer dataset
import pandas as pd
beer = pd.read_csv('data.txt', sep=' ')
beer
2.抽取数据X
X = beer[["calories","sodium","alcohol","cost"]]
print(X)
3.K-means clustering创建实例
from sklearn.cluster import KMeans

km = KMeans(n_clusters=3).fit(X)
km2 = KMeans(n_clusters=2).fit(X)

4.结果：获取分类结果
km.labels_

5.加载到原始数据
beer['cluster'] = km.labels_
beer['cluster2'] = km2.labels_
beer.sort_values('cluster')

2.绘图验证

（1）求每一类中心点：聚合函数groupby

1.获取中心值
from pandas.tools.plotting import scatter_matrix
%matplotlib inline

cluster_centers = km.cluster_centers_

cluster_centers_2 = km2.cluster_centers_
2.groupby：求取三个类簇的聚类中心点值
（1）
beer.groupby("cluster").mean()
（2）
beer.groupby("cluster2").mean()
结果：
	calories	sodium	alcohol	cost	cluster
cluster2					
0	91.833333	10.166667	3.583333	0.433333	1.333333
1	150.000000	17.000000	4.521429	0.520714	0.000000

3.重新排序
centers = beer.groupby("cluster").mean().reset_index() #按照对应分组类别
结果：
centers为
   cluster  calories  sodium   alcohol      cost  cluster  cluster2
0        0     70.00    10.5  2.600000  0.420000         1         1
1        1    150.00    17.0  4.521429  0.520714         0         0
2        2    102.75    10.0  4.075000  0.440000         1         2

（2）绘图验证

 绘制两个特征的图以及中心点

%matplotlib inline
import matplotlib.pyplot as plt
plt.rcParams['font.size'] = 14

import numpy as np
colors = np.array(['red', 'green', 'blue', 'yellow'])

---------
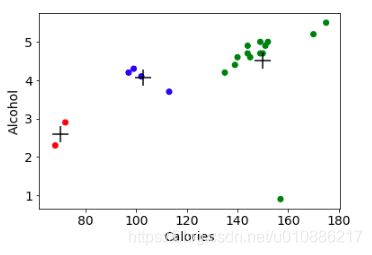
plt.scatter(beer["calories"], beer["alcohol"],c=colors[beer["cluster"]])

plt.scatter(centers.calories, centers.alcohol, linewidths=3, marker='+', s=300, c='black')

plt.xlabel("Calories")
plt.ylabel("Alcohol")

结果：

（3）两两特征分析

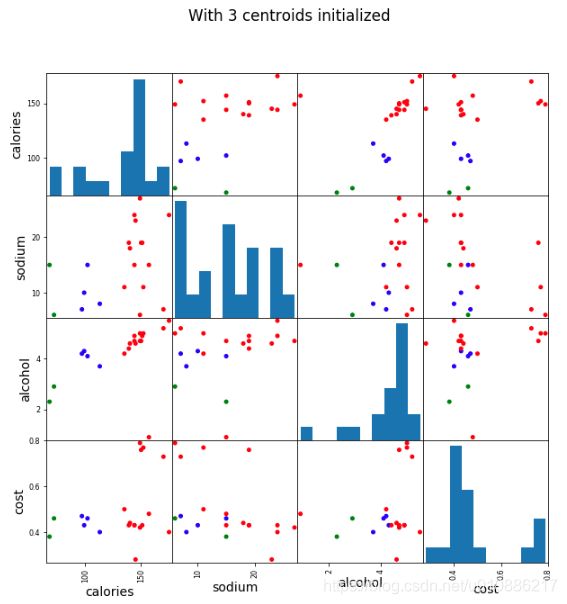
（a）三个簇

scatter_matrix(beer[["calories","sodium","alcohol","cost"]],s=100, alpha=1, c=colors[beer["cluster"]], figsize=(10,10))
plt.suptitle("With 3 centroids initialized")

（2）两个簇

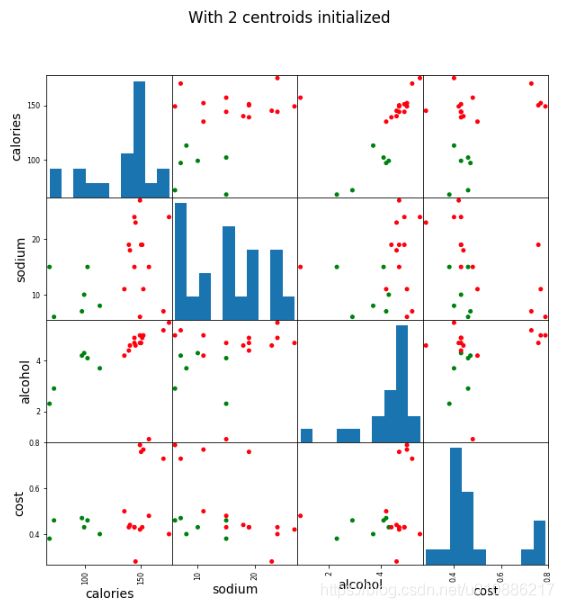
scatter_matrix(beer[["calories","sodium","alcohol","cost"]],s=100, alpha=1, c=colors[beer["cluster2"]], figsize=(10,10))
plt.suptitle("With 2 centroids initialized")

结果：

 

七、归一化改进Scaled data

1.归一化
四个特征值基本都在[-2,2]之间，消除差异

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
X_scaled

2.KMeans拟合

km = KMeans(n_clusters=3).fit(X_scaled)

3.结果添加到原始数据上

beer["scaled_cluster"] = km.labels_
beer.sort_values("scaled_cluster")

4.求取每个簇的中心点

beer.groupby("scaled_cluster").mean()

5.绘制两两特征的关系

pd.scatter_matrix(X, c=colors[beer.scaled_cluster], alpha=1, figsize=(10,10), s=100)

6.优劣势

（1）优势：使每个特征的权重相似，不至于忽略较小，但是比较重要的特征。

（2）劣势：可能有的特征比较大，而且非常重要。这样会抹杀掉该特征的重要性。

八、聚类评估：轮廓系数（Silhouette Coefficient ）

1.公式

（1）单点的轮廓系数

（2）将所有点的轮廓系数求平均，就是该聚类结果总的轮廓系数

2.概念：

（1）ai：计算样本i到同簇其他样本的平均距离ai。ai 越小，说明样本i越应该被聚类到该簇。将ai 称为样本i的簇内不相似度。
（2）bi：计算样本i到其他某簇Cj 的所有样本的平均距离bij，称为样本i与簇Cj 的不相似度。定义为样本i的簇间不相似度：bi =min{bi1, bi2, ..., bik}
（3）结果：轮廓系数si
si接近1，则说明样本i聚类合理
si接近-1，则说明样本i更应该分类到另外的簇
若si 近似为0，则说明样本i在两个簇的边界上。

（4）将所有点的轮廓系数求平均，就是该聚类结果总的轮廓系数！

3.代码实现

from sklearn import metrics
score = metrics.silhouette_score(X,beer.cluster) #归一化前的结果
score_scaled = metrics.silhouette_score(X,beer.scaled_cluster) #归一化后的结果
print(score_scaled, score)

结果：
0.673177504646 0.179780680894 

解释：
归一化后反而变差，因为，可能会消除部分重要的特征的值。

4.选择k值可以，循环看轮廓系数得分，选择轮廓系数偏高的值

scores = []
for k in range(2,20):
    labels = KMeans(n_clusters=k).fit(X).labels_
    score = metrics.silhouette_score(X, labels)
    scores.append(score)

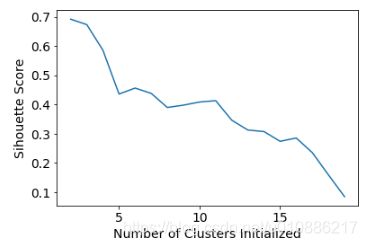
scores

5.绘图

plt.plot(list(range(2,20)), scores)
plt.xlabel("Number of Clusters Initialized")
plt.ylabel("Sihouette Score")

结果：
[0.6917656034079486,
 0.6731775046455796,
 0.5857040721127795,
 0.4355716067265817,
 0.4559182167013378,
 0.43776116697963136,
 0.38946337473126,
 0.39746405172426014,
 0.4081599013899603,
 0.41282646329875183,
 0.3459775237127248,
 0.31221439248428434,
 0.30707782144770296,
 0.2736836031737978,
 0.2849514001174898,
 0.23498077333071996,
 0.1588091017496281,
 0.08423051380151177]

6.绘图

plt.plot(list(range(2,20)), scores)
plt.xlabel("Number of Clusters Initialized")
plt.ylabel("Sihouette Score")