K-Means聚类算法--步骤+代码

0.介绍

聚类和分类算法的最大区别在于，分类的目标类别为已知（监督学习），而聚类的目标类别是未知的（非监督）。K_Means算法（K_均值算法）就是无监督算法之一

1.原理

---

对于给定的样本集，按照样本之间的距离大小，将样本集划分为K个簇。让簇内的点尽量紧密的连在一起，而让簇间的距离尽量的大。

---

数据表达式：
假设簇划分为$(C_1,C_2，...C_k)$，则我们的目标是最小化平方误差E：
$$E=\sum _{i=1}^K\sum _{x\in C_i}||x-{\mu }_i|{|}_2^2$$
其中$u_i$是$C_i$的均值向量，有时也称质心，表达式为：
$$u_i=\frac{1}{|C_i|}\sum _{x\in C_i}x$$
如果我们想直接求上式的最小值并不容易，这是一个NP难的问题，因此只能采用启发式的迭代方法。
下图就可以形象的描述

上图a表达了初始数据集，假设K=2，在b图中，我们随机选择两个k类所对应的质心，即图中的红色质心和蓝色质心，然后分别计算样本中所有的点到两个质心的距离，并标记每个样本的类别为该样本距离最小质心的类别，如c图所示。此时对当前标记为红色和蓝色的点分别求其新的质心，如图d。图e和图f重复了我们在图c和图d的过程，即将所有点的类别标记为距离最近的质心并求新的质心。最终得到两个类别如图f。
这是无监督分类，即没有原始标签，我们将数据集分类。在实际K_Means算法中，一般会多次运行图c和图d，即迭代，才能达到最终比较优的类别。

2.算法步骤

2.1步骤描述

输入时样本集$D=\{x_1,x_2,..{.}_m\}$,
聚类的簇数k；
输出是簇划分$C=\{C_1,C_2,...C_k\}$。
1）数据准备
2）对于未聚类数据集，首先从数据集D中随机选择 k样本作为初始的k 个质心，如图红色五角星所示：

3）求出每个样本到中心点的距离，按照距离自身最近的中心点进行第一次聚类，如图：

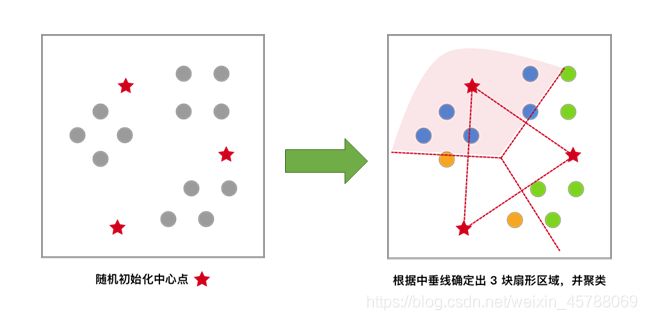
4）依据上次聚类结果，求出新的中心点（新簇内点x和y的平均值）

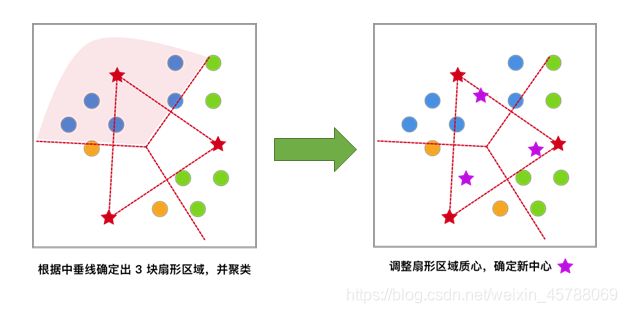
5）反复迭代，直到中心点的变化满足收敛条件（变化很小或几乎不变化），最终得到聚类结果

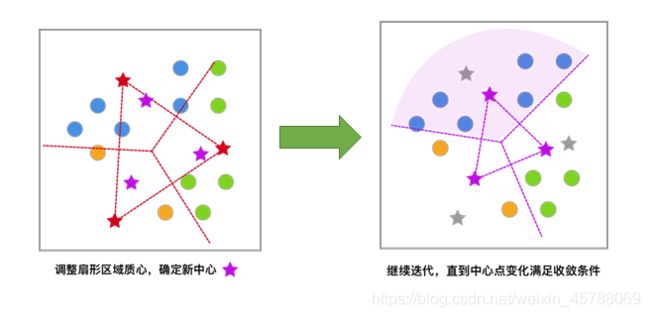
2.2关于K值的选择

1）手肘法

SSE(sum of the squared errors，误差平方和)

手肘法的核心思想：

• 随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。
• 当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说SSE和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的真实聚类数。

2）轮廓系数
使用轮廓系数(silhouette coefficient)来确定，选择使系数较大所对应的k值。

2.3距离度量（欧式距离）

将对象点分到距离聚类中心最近的那个簇质点的距离
欧氏距离公式：
$$d(x,y)=\sqrt{\sum _{i=0}^n(x_i-y_i{)}^2}$$

3、代码实现

import numpy as np
import random
import matplotlib.pyplot as plt

#质心集：数组；
#数据集：列表；
#簇：字典

def loadDataSet(filename):
    data_get = []
    fp = open(filename, 'r')
    for line in fp:
        curline = line.split(' ')
        floatline = list(map(float,curline))
        data_get.append(floatline)
    return data_get
    
def findCentroids(data_get,k):    #获取k个质心
    m = random.sample(data_get, k)
    return np.array(m)

def distEclud(vecA,vecB):     #计算距离--欧式距离
    return np.sqrt(sum(np.power(vecA-vecB,2)))

def Kmeans(data_get,centroidsList):   #划分簇
#    np.array(data_get)     #将数据集转为数组
    distculde = {}   #建立一个字典
    flag = 0        #元素分类标记，记录与相应聚类距离最近的那个类
    for data in data_get:
        vecA = np.array(data)
        minDis = float('inf')     #始化为最大值
        for i in range(len(centroidsList)):
            vecB = centroidsList[i]
            distance = distEclud(vecA, vecB)    #计算距离
            if distance < minDis:     #直至找出距离最小的质点
                minDis = distance
                flag = i
        if flag not in distculde.keys():
            distculde[flag] = list()
        distculde[flag].append(data)
    return distculde

def getCentroids(distculde):   #得到新的质心
    newcentroidsList = []     #建立新质点集
    for key in distculde:    
        cent = np.array(distculde[key])       #将列表转为数组，便于计算
        newcentroid = np.mean(cent,axis=0)     #计算新质点，对x和y分别求和，再平均
        newcentroidsList.append(newcentroid.tolist())     #添加每个质心，得从数组转化为列表添加
    return np.array(newcentroidsList)     #返回新质点数组

def calculate_Var(distculde, centroidsList):
    #计算聚类间的均方误差
    item_sum = 0.0
    for key in distculde:
        vecA = centroidsList[key]
        dist = 0.0
        for item in distculde[key]:
            vecB = np.array(item)
            dist += distEclud(vecA, vecB)
        item_sum += dist
    return item_sum
        
def showCluster(distculde, centroidsList):
    #画聚类图像
    x = []
    y = []
    x.append(centroidsList[:,0].tolist())
    y.append(centroidsList[:,1].tolist())
    plt.plot(x, y,'k*')     #画质点，为黑色*
    colourList = ['bo', 'ro', 'yo', 'co']
    for i in distculde:
        #获取每簇
        centx = []
        centy = []
        for item in distculde[i]:
            centx.append(item[0])
            centy.append(item[1])
        plt.plot(centx, centy, colourList[i])   #画簇
    plt.show()

if __name__ == "__main__":
    k = 4
    datMat = loadDataSet('1.txt')
    centroidsList = findCentroids(datMat, k)     #随机获得k个聚类中心
    distculde = Kmeans(datMat,centroidsList)     #第一次聚类迭代
    newVar = calculate_Var(distculde,centroidsList)   
    oldVar = -0.0001   #初始化均方误差
    while abs(newVar - oldVar) >= 0.0001:
        centroidsList = getCentroids(distculde)
        distculde = Kmeans(datMat, centroidsList)
        oldVar = newVar
        newVar = calculate_Var(distculde, centroidsList)
    showCluster(distculde,centroidsList)
    

输出（plot图格）：

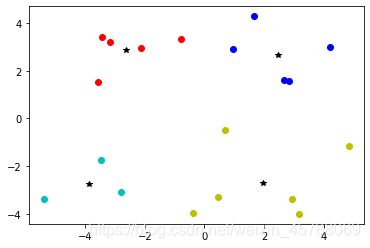
黑星代表中心点（黑星是不在簇中），一种颜色代表一簇；
每次跑出来的结果（图像）都不一样，因为初始化是随机选择，因此最后的簇也就不一样

文本"1.txt"数据：

空格分隔

1.658985 4.285136
-3.453687 3.424321
4.838138 -1.151539
-5.379713 -3.362104
0.972564 2.924086
-3.567919 1.531611
0.450614 -3.302219
-3.487105 -1.724432
2.668759 1.594842
-3.156485 3.191137
3.165506 -3.999838
-2.786837 -3.099354
4.208187 2.984927
-2.123337 2.943366
0.704199 -0.479481
-0.392370 -3.963704
2.831667 1.574018
-0.790153 3.343144
2.943496 -3.357075

4.优缺点

优点：

1. 属于无监督学习，无须准备训练集；
2. 原理比较简单，实现起来容易；
3. 结果可解释性较好。

缺点：

1. 聚类数目K的选取，选择不恰当的K值可能会导致糟糕的聚类效果；
2. 可能收敛到局部最优，在大规模上数据收敛较慢；
3. 对噪音、异常点比较的敏感。

5、传统K-means改进

在学习了传统K-means算法的基础上,我们清楚了K-means的局限性,因此我们将要说一下K-Means的优化变体方法。这其中包括初始化优化K-Means++, 距离计算优化elkan K-Means算法和大数据情况下的优化Mini Batch K-Means算法。

初始化优化K-means++

---

k个初始化的质心的位置选择对最后的聚类结果和运行时间都有很大的影响，因此需要选择合适的k个质心。如果仅仅是完全随机的选择，有可能导致算法收敛很慢。K-Means++算法就是对K-Means随机初始化质心的方法的优化。

---

K-Means++的对于初始化质心的优化策略也如下：

• a）从输入的数据点集合中随机选择一个点作为第一个聚类中心$u_1$
• b）对于数据集中的每一个点xi，计算它与已选择的聚类中心中最近聚类中心的距离$D(x_i)=argmin||x_i-u_r|{|}_2^{2}r=1,2,...k_{selected}$
  arg min 就是使后面这个式子达到最小值时的变量的取值
• c）选择一个新的数据点作为新的聚类中心，选择的原则是：$D(x)$较大的点，被选取作为聚类中心的概率较大
• d）重复b和c直到选择出k个聚类质心
• e）利用这k个质心来作为初始化质心去运行标准的K-Means算法

距离计算优化elkan K-means

在传统的K-Means算法中，我们在每轮迭代时，要计算所有的样本点到所有的质心的距离，这样会比较的耗时。那么，对于距离的计算有没有能够简化的地方呢？elkan K-Means算法就是从这块入手加以改进。它的目标是减少不必要的距离的计算。那么哪些距离不需要计算呢？

elkan K-Means利用了两边之和大于等于第三边,以及两边之差小于第三边的三角形性质，来减少距离的计算。

• 第一种规律是对于一个样本点$x$和两个质心${\mu }_{j1},{\mu }_{j2}$。如果我们预先计算出了这两个质心之间的距离$D_{(j_1,j_2)}$，则如果计算发现$2D(x,j_1)\le D(j_1,j_2)$,我们立即就可以知道$D(x,j_1)\le D(x,j_2)$。此时我们不需要再计算D(x,j_2),也就是说省了一步距离计算。

• 第二种规律是对于一个样本点$x$和两个质心${\mu }_{j1},\mu j2$。我们可以得到$D(x,j_2)\ge max0,D(x,j_1)-D(j_1,j_2)$。这个从三角形的性质也很容易得到。

• 利用上边的两个规律，elkan K-Means比起传统的K-Means迭代速度有很大的提高。但是如果我们的样本的特征是稀疏的，有缺失值的话，这个方法就不使用了，此时某些距离无法计算，则不能使用该算法。

大样本优化Mini Batch K-Means

• 在统的K-Means算法中，要计算所有的样本点到所有的质心的距离。如果样本量非常大，比如达到10万以上，特征有100以上，此时用传统的K-Means算法非常的耗时，就算加上elkan K-Means优化也依旧。在大数据时代，这样的场景越来越多。此时Mini Batch K-Means应运而生。

• 顾名思义，Mini Batch，也就是用样本集中的一部分的样本来做传统的K-Means，这样可以避免样本量太大时的计算难题，算法收敛速度大大加快。当然此时的代价就是我们的聚类的精确度也会有一些降低。一般来说这个降低的幅度在可以接受的范围之内。

• 在Mini Batch K-Means中，我们会选择一个合适的批样本大小batch size，我们仅仅用batch size个样本来做K-Means聚类。那么这batch size个样本怎么来的？一般是通过无放回的随机采样得到的。

• 为了增加算法的准确性，我们一般会多跑几次Mini Batch K-Means算法，用得到不同的随机采样集来得到聚类簇，选择其中最优的聚类簇。