梯度逆转的原理及其应用

摘要
近期项目中应用到了梯度逆转，在此对近期学习和使用梯度逆转的心得进行记录。

若有任何错误，欢迎指正批评！

参考文献：Unsupervised domain adaptation by backpropagation

• 原文背景是域适应(domain adaptation)问题，有关域适应的解释请参考此文
  

文章思路简述

• 因为原文的目的是域适应，简单来说，就是将一个在源域上训练好的模型迁移到目标域时，要求模型在目标域也要极可能有更好的表现。其本质就是在两种不同但类似的分布的数据集之间寻找一种“迁移”。

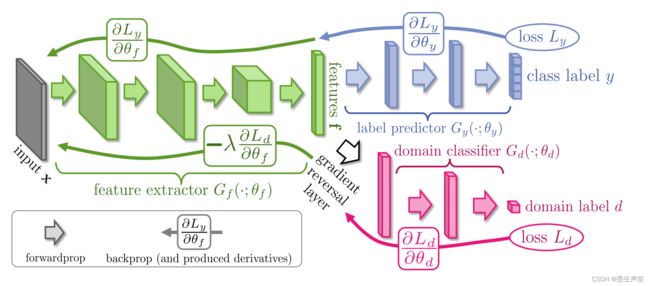
• 正向传播时：

  • 蓝色部分：label predictor Gy 用来预测样本的标签。通过min $L_y$ 提高其预测能力，因为原文中做的是手写数字识别，故这里是一个分类器，在其他任务中也可以是回归预测器。
  • 红色部分：domain classifier Gd 是一个二分类器，用来预测样本来自源域还是目标域。通过min $L_d$提高其对源域和目标域的分类能力。
  • 绿色部分：是一个Encoder，通过输入数据x提取特征f。

• 反向传播时：

  • 绿色和蓝色的组合，与传统分类任务一样，正常反向传播其梯度。
  • 绿色和红丝的组合，在反向传播过程中增加了一个梯度逆转，该层直接在原有梯度前增加一个$-\lambda$ 以此实现在优化过程中最大化二分类误差$L_d$，目的是使得Encoder得到的feature尽可能让源域与目标域之间区分不开，也就实现了原文中提到的domain adaptation/domain invariance域自适应。

总的来说，整个网络模型在梯度逆转层的作用下，使得feature extractor在提取特征时能更好地提取到源域和目标域共有的特征，使得网络在目标域上依然保持优秀的的预测能力。

除此之外，通过实验观察到，在应用了梯度逆转之后，模型能够更快更好的提升其正向预测的能力。

手写字识别的应用

为了验证梯度逆转的实际效果，作者在手写字分类中尝试应用了梯度逆转。

• 首先设置了一个特殊的任务场景，将MINIST数据集分为两类，其一是所有的数字0样本，其二是其他样本。然后以随机的方式，设置两种样本，一种是由数字0样本和其他样本合并而成，另一种是由两个其他样本合并而成。对于含有数字0的样本，标签为1，不含数字0的样本，标签为0。

def gen_new(x):
    other_set = []
    target_set = []
    target = 0
    for i in tqdm(range(len(x_train))):
        if y_train[i] != target:
            other_set.append(x_train[i])
        elif y_train[i] == target:
            target_set.append(x_train[i])
    print(len(target_set))
    randList = np.random.randint(0,2,len(target_set[:4000]))
    new_data = []
    j = 0
    for i in tqdm(randList):
        if i == 1:
            new_data.append(other_set[j] + target_set[j])
        elif i == 0:
            new_data.append(other_set[j] + other_set[j+1])
        j+=1
    new_data = new_data
    label1 = []
    for i in randList:
        if i == 0:
            label1.append(torch.tensor(0))
        elif i == 1:
            label1.append(torch.tensor(1))
    label0 = []
    for i in randList:
        if i == 0:
            label0.append(torch.tensor(1))
        elif i == 1:
            label0.append(torch.tensor(0))
    return new_data,label1,label0

• 之后设计了一个简单的网络模型，包括梯度逆转层的实现

class GradientReverseFunction(Function):
    """
    重写自定义的梯度计算方式
    """
    @staticmethod
    def forward(ctx: Any, input: torch.Tensor, coeff: Optional[float] = 1.) -> torch.Tensor:
        ctx.coeff = coeff
        output = input * 1.0
        return output
    @staticmethod
    def backward(ctx: Any, grad_output: torch.Tensor) -> Tuple[torch.Tensor, Any]:
        return grad_output.neg() * ctx.coeff, None
class GRL_Layer(nn.Module):
    def __init__(self):
        super(GRL_Layer, self).__init__()
    def forward(self, *input):
        return GradientReverseFunction.apply(*input)
class Mnist_NN2(nn.Module):
    def __init__(self):
        super(Mnist_NN2,self).__init__()
        self.hidden1 = nn.Sequential(         
            nn.Conv2d(
                in_channels=1,              
                out_channels=16,            
                kernel_size=5,              
                stride=1,                   
                padding=2,                  
            ),                              
            nn.ReLU(),                      
            nn.MaxPool2d(kernel_size=2),   
        )
        self.hidden2 = nn.Sequential(         
            nn.Conv2d(16, 36, 5, 1, 2),     
            nn.ReLU(),                      
            nn.MaxPool2d(2),                
        )
        self.out  = nn.Linear(1764, 2)
        self.advout = nn.Linear(1764,2)
        self.grl = GRL_Layer()
    def forward(self, x):
        x = F.relu(self.hidden1(x))
        x = F.relu(self.hidden2(x))
        x = x.view(x.size(0), -1) 
        pre1 = self.out(x)
        rgx = self.grl(x)
        pre2 = self.advout(rgx)
        return x,pre1,pre2

• 训练代码

x_train = x_train.reshape(2000,1,28,28)
bs = 1000 # batch size
train_ds = TensorDataset(x_train, y_train, advy_train)
train_dl = DataLoader(train_ds, batch_size=bs, shuffle=True)
path = 'feature17'
os.makedirs(f'{path}/')
device = "cuda:0"
def lossfn(prex,advx,label,adv_label):
    return F.cross_entropy(prex,label) + F.cross_entropy(advx,adv_label)
epochs = 1000
net = Mnist_NN2()
net.to(device)
# optimizer = optim.Adam(net.parameters(),lr = 0.001)
optimizer = optim.SGD(net.parameters(),lr = 0.001)
loss_set = []
acc_set = []
advacc_set = []
feature_set = []
revs_set = []
advrevs_set = []
for epoch in tqdm(range(epochs)):
    epoch_losses = []
    epoch_rights = []
    advepoch_rights = []
    epoch_revs = []
    epoch_advrevs = []
    for x,y,adv_y in train_dl:
        x = x.to(device)
        y = y.to(device)
        adv_y = adv_y.to(device)
        feature,pre1,pre2 = net(x)
#         正常分类
        res = nn.functional.softmax(pre1)
        pre = torch.max(res.data,1)[1]
        rights = pre.eq(y.data.view_as(pre)).sum()
        epoch_rights.append(rights/bs)
#         对抗分类
        advres = nn.functional.softmax(pre2)
        advpre = torch.max(advres.data,1)[1]
        advrights = advpre.eq(y.data.view_as(advpre)).sum()
        advepoch_rights.append(advrights/bs)

        loss = lossfn(pre1,pre2,y,adv_y)
        epoch_losses.append(loss)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
       
    epoch_loss = sum(epoch_losses)/len(epoch_losses)
    epoch_acc = sum(epoch_rights)/len(epoch_rights)
    advepoch_acc = sum(advepoch_rights)/len(advepoch_rights)
    loss_set.append(epoch_loss)
    acc_set.append(epoch_acc)
    advacc_set.append(advepoch_acc)

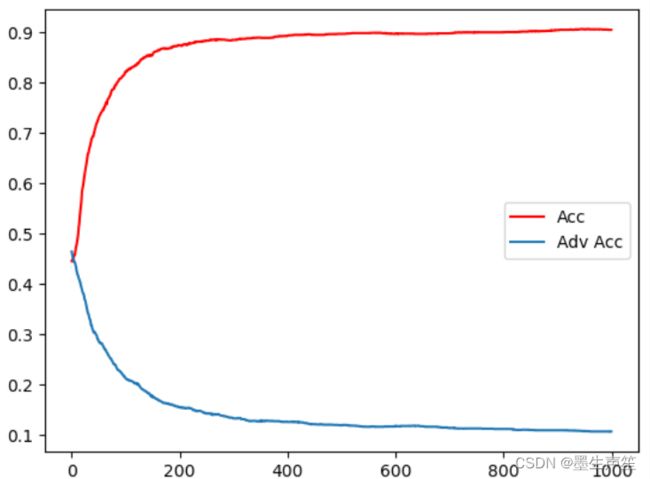
• 结果展示

acc_set_cpu = [acc.cpu().detach() for acc in acc_set]
advacc_set_cpu = [advacc.cpu().detach() for advacc in advacc_set]
plt1 = plt.plot(np.arange(len(acc_set_cpu)),acc_set_cpu,c = 'r',label = 'Acc')
plt2 = plt.plot(np.arange(len(advacc_set_cpu)),advacc_set_cpu,label = 'Adv Acc')
plt.legend()
plt.show()
plt.close()   

• 结果说明：对抗预测器努力想要识别出样本中除了0以外的其他信息，但由于梯度逆转层的作用，导致特征提取器会弱化非0的特征在feature中的占比，以此来促进预测器对数字0的识别。
• 此结果证明了，梯度逆转的对抗作用可以有效帮助正向预测器，更好的进行预测。因为正向预测器自我精进的同时，特征提取器也在不断提高对数字0的提取能力，以此来帮助整个网络模型提高对数字0的识别能力。

应用推广

这种对抗方法还可以应用在很多领域。例如，在股市预测的任务中，需要对原始数据中的超额特征和市场特征进行区分，即可使用此方法，尽可能提高模型对两种特征的区分能力。

更多应用场景欢迎补充！