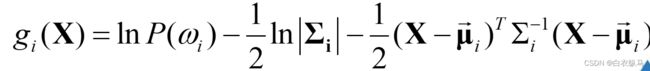最小错误率的贝叶斯决策和最大似然比判别规则
数据集介绍:
Iris数据集是常用的分类实验数据集,由Fisher, 1936收集整理。Iris也称鸢尾花卉数据集,是一类多重变量分析的数据集。数据集包含150个数据样本,分为3类,每类50个数据,每个数据包含4个属性。可通过花萼长度,花萼宽度,花瓣长度,花瓣宽度4个属性预测鸢尾花卉属于(Setosa,Versicolour,Virginica)三个种类中的哪一类。
1.最小错误率的贝叶斯决策
需求:
设计三基于最小错误率的贝叶斯决策算法并编码实现。对3个类别,将测试样本两两分组进行分类测试。在每两组进行分类时,令待分类样本的先验概率,
去掉与类别无关的项之后,判别函数可以简化为:
协方差矩阵:![]()
对Iris数据集中的样本进分类:抽取每一类样本的前40个构建训练集;抽取每类样本的后10个构建测试集
N = 120;%120个作为训练样本
w = 3;%类别数
n = 4;%特征数
N1 = 40;
N2 = 40;
N3 = 40;%各类样本数
data=xlsread('D:\MATLABdata\data\Iris.xls');
%导入数据
A = data(1:40,:);
B = data(51:90,:);
C = data(101:140,:);
%训练集构建
a = data(41:50,:);
b = data(91:100,:);
c = data (141:150,:);
%测试集构建
X1 = mean(A);
X2 = mean(B);
X3 = mean(C);
%求训练样本的均值
S1 = cov(A);
S2 = cov(B);
S3 = cov(C);
%求训练样本的协方差矩阵
S1_ = inv(S1);
S2_ = inv(S2);
S3_ = inv(S3);
%求训练样本的协方差矩阵的逆矩阵
S11 = det(S1);
S22 = det(S2);
S33 = det(S3);
%求训练样本协方差矩阵的行列式
pw = 0.5;
%先验概率为0.5
w1=0;
w2=0;
w3=0;
%取第一类测试样本,按w1,w2分类
for k = 1:10
p1 =-1/2 * (a(k,:)-X1)*S1_*(a(k,:)-X1)'+log(pw)-1/2*log(S11);
p2 =-1/2 * (a(k,:)-X2)*S2_*(a(k,:)-X2)'+log(pw)-1/2*log(S22);
if p1>p2
w1=w1+1;
else
w2=w2+1;
end
end
fprintf('取第一类测试样本,按w1,w2分类,其中分给w1:%d个,分给w2:%d个\n',w1,w2);
w1=0;
w2=0;
w3=0;
%取第一类测试样本,按w1,w3分类
for k = 1:10
p1 =-1/2 * (a(k,:)-X1)*S1_*(a(k,:)-X1)'+log(pw)-1/2*log(S11);
p3 =-1/2 * (a(k,:)-X3)*S3_*(a(k,:)-X3)'+log(pw)-1/2*log(S33);
if p1>p3
w1=w1+1;
else
w3=w3+1;
end
end
fprintf('取第一类测试样本,按w1,w3分类,其中分给w1:%d个,分给w3:%d个\n',w1,w3);
w1=0;
w2=0;
w3=0;
%取第二类测试样本,按w2,w3分类
for k = 1:10
p3 =-1/2 * (b(k,:)-X3)*S3_*(b(k,:)-X3)'+log(pw)-1/2*log(S33);
p2 =-1/2 * (b(k,:)-X2)*S2_*(b(k,:)-X2)'+log(pw)-1/2*log(S22);
if p2>p3
w2=w2+1;
else
w3=w3+1;
end
end
fprintf('取第二类测试样本,按w2,w3分类,其中分给w3:%d个,分给w2:%d个\n',w3,w2);
w1=0;
w2=0;
w3=0;
%取第二类测试样本,按w1,w2分类
for k = 1:10
p1 =-1/2 * (b(k,:)-X1)*S1_*(b(k,:)-X1)'+log(pw)-1/2*log(S11);
p2 =-1/2 * (b(k,:)-X2)*S2_*(b(k,:)-X2)'+log(pw)-1/2*log(S22);
if p1>p2
w1=w1+1;
else
w2=w2+1;
end
end
fprintf('取第二类测试样本,按w1,w2分类,其中分给w1:%d个,分给w2:%d个\n',w1,w2);
w1=0;
w2=0;
w3=0;
%取第三类测试样本,按w1,w3分类
for k = 1:10
p1 =-1/2 * (c(k,:)-X1)*S1_*(c(k,:)-X1)'+log(pw)-1/2*log(S11);
p3 =-1/2 * (c(k,:)-X3)*S3_*(c(k,:)-X3)'+log(pw)-1/2*log(S33);
if p1>p3
w1=w1+1;
else
w3=w3+1;
end
end
fprintf('取第三类测试样本,按w1,w3分类,其中分给w1:%d个,分给w3:%d个\n',w1,w3);
w1=0;
w2=0;
w3=0;
%取第三类测试样本,按w2,w3分类
for k = 1:10
p2 =-1/2 * (c(k,:)-X2)*S2_*(c(k,:)-X2)'+log(pw)-1/2*log(S22);
p3 =-1/2 * (c(k,:)-X3)*S3_*(c(k,:)-X3)'+log(pw)-1/2*log(S33);
if p2>p3
w2=w2+1;
else
w3=w3+1;
end
end
fprintf('取第三类测试样本,按w2,w3分类,其中分给w2:%d个,分给w3:%d个\n',w2,w3);
%去掉第二特征之后画图
d1 = data(:,1:1);
d2 = data(:,3:4);
d = [d1 d2];
X11=[X1(:,1:1) X1(:,3:4)]
X22=[X2(:,1:1) X2(:,3:4)]
X33=[X3(:,1:1) X3(:,3:4)]
A1 = d(1:40,:);
B1 = d(51:90,:);
C1 = d(101:140,:);
Sa = cov(A1);%协方差矩阵
Sa_ = inv(Sa);%协方差的逆矩阵
SSa = det(Sa);%协方差矩阵的行列式
Sb = cov(B1);%协方差矩阵
Sb_ = inv(Sb);%协方差的逆矩阵
SSb = det(Sb);%协方差矩阵的行列式
Sc = cov(C1);%协方差矩阵
Sc_ = inv(Sc);%协方差的逆矩阵
SSc = det(Sc);%协方差矩阵的行列式
for k = 1:150
p1 = -1/2 * (d(k,:)-X11)*Sa_*(d(k,:)-X11)'+log(pw)-1/2*log(SSa);
p2 =-1/2 * (d(k,:)-X22)*Sb_*(d(k,:)-X22)'+log(pw)-1/2*log(SSb);
p3 =-1/2 * (d(k,:)-X33)*Sc_*(d(k,:)-X33)'+log(pw)-1/2*log(SSc);
p =[p1 p2 p3];
pmax = max(p);
if pmax == p1
w =1;
plot3(d(k,1),d(k,2),d(k,3),'b*');grid on;hold on;
elseif pmax == p2
w = 2;
plot3(d(k,1),d(k,2),d(k,3),'r+');grid on;hold on;
elseif pmax == p3
w = 3;
plot3(d(k,1),d(k,2),d(k,3),'g>');grid on;hold on;
title('去除第二特征之后的基于最小错误率的贝叶斯决策');
end
end
2.最大似然比判别规则
要求:
对Iris数据集中的样本进分类:随机抽取每一类30个样本构建训练集;每类剩余20个样本构建测试集。
设计基于最小错误率的贝叶斯决策算法并编码实现。对3个类别,令待分类样本的先验概率为1/3
data=xlsread('D:\MATLABdata\data\Iris.xls');
%导入数据
A = data(1:50,:);
B = data(51:100,:);
C = data(101:150,:);
a = [];
b = [];
c = [];
index1 = randperm(50);
index2 = randperm(50);
index3 = randperm(50);
for i = index1
a=[a;A(i,:)];
end
for i = index2
b=[b;B(i,:)];
end
for i = index3
c=[c;C(i,:)];
end
a_train = a(1:30,:);
b_train = b(1:30,:);
c_train = c(1:30,:);
%训练集
a_test = a(31:50,:);
b_test = b(31:50,:);
c_test = c(31:50,:);
%测试集
pw = 1/3;
%先验概率都为1/3
a_mean = mean(a_train);
b_mean = mean(b_train);
c_mean = mean(c_train);
%训练样本的均值
a_cov = cov(a_train);
b_cov = cov(b_train);
c_cov = cov(c_train);
%训练样本的协方差矩阵
[w1,w2,w3]=likelihood(a_test,a_mean,b_mean,c_mean,a_cov,b_cov,c_cov);
fprintf('利用第一类训练,测试分为w1类:%d个,w2类:%d个,w3类:%d个\n',w1,w2,w3)
[w1,w2,w3]=likelihood(b_test,a_mean,b_mean,c_mean,a_cov,b_cov,c_cov);
fprintf('利用第二类训练,测试分为w1类:%d个,w2类:%d个,w3类:%d个\n',w1,w2,w3)
[w1,w2,w3]=likelihood(c_test,a_mean,b_mean,c_mean,a_cov,b_cov,c_cov);
fprintf('利用第三类训练,测试分为w1类:%d个,w2类:%d个,w3类:%d个\n',w1,w2,w3)