Useful Policy Invariant Shaping from Arbitrary Advice论文翻译导读分析

这是

摘要

强化学习（RL）是一种强大的学习范式，在该范式中，agent可以学习最大化稀疏和延迟的奖励信号。尽管RL在复杂领域取得了许多令人印象深刻的成功，但学习可能需要数小时、数天甚至数年的训练数据。当代RL研究的一个主要挑战是发现如何用更少的数据学习。以前的工作表明，域信息可以成功地用于塑形奖励；通过添加额外的奖励信息，agent可以用更少的数据学习。此外，如果奖励是由一个势能函数构造的，则最优策略保证不变。虽然这种基于势能的奖励塑形(PBRS)有希望，但它受到对一个明确定义的势能函数的需求的限制。理想情况下，我们希望能够采纳来自人或其他agent的任意建议，并在不影响最优策略的情况下提高性能。最近提出的基于动态势能的建议(dynamic potential based advice，DPBA)方法通过接受来自人或其他agent的任意建议来解决这一问题，并在不影响最优策略的情况下提高性能。本文的主要贡献是从理论和经验上揭示了 DPBA 的一个缺陷。或者，为了实现理想目标，我们提出了一种称为策略不变显式塑形 (policy invariant explicit shaping，PIES) 的简单方法，并从理论上和经验上证明 PIES 在 DPBA 失败的地方成功。

1. INTRODUCTION

----强化学习（RL）agent旨在学习最大化奖励信号的策略(然而，最大化的奖励信号并不一定是正确的策略，因为agent可能会刷分，也就是 reward hacking)（从状态到动作的映射）[17]。在许多情况下，奖励信号是稀疏和延迟的，因此学习一个好的策略可能需要很长时间。例如，Open AI Five agent[13]每天训练需要180年的游戏经验；同样，大师级星际争霸特工Alpha Star[18]需要16000场比赛作为训练数据。一种加速学习的方法是添加外部建议（advice）。为 RL agent提供额外奖励以改善学习的做法称为奖励塑形，额外奖励称为塑形奖励。然而，天真地增加原来的奖励函数与塑形可能会改变 RL agent的最优策略[15]。例如，Randløv 和 Alstrøm [15]表明，增加一个塑形奖励(一开始看起来是合理的)会导致一个机构学习如何骑自行车朝目标前进，而不是“分心”，骑在一个循环，反复收集塑形奖励。
----基于势能的奖励塑形(Potential based reward shaping，PBRS)[12,19,20]允许 RL agent通过从势能函数获得塑形奖励，在不改变其最优策略的情况下纳入外部建议。给定一个静态势函数，PBRS 将塑形奖励定义为当agent从一个状态转换到另一个状态时状态(或状态-行动对)的势能差。Ng 等[12]证明了 PBRS 是保证策略不变的: 使用 PBRS 不会改变最优策略。
----虽然PBRS实现了策略不变性，但个人或agent可能很难或不可能将其建议表达为基于势能的函数。相反，最好允许以任意函数的形式使用更直接或更直观的建议。那么，理想的奖励塑形方法将具有三个特性:

1. 能够使用任意的奖励函数作为建议，
2. 在附加建议存在的情况下保持最优策略不变，
3. 当建议是好的时候提高 RL agent的学习速度。

----Harutyunyan等人[8]试图通过提出基于动态势能的建议（dynamic potential-based advice ，DPBA）框架来解决同样的问题，其中的想法是从任意建议中动态学习势能函数，然后可以使用该函数来定义塑形奖励。重要的是，作者声称，如果将势能函数初始化为零，则DPBA保证是策略不变的。我们在这项工作中表明，这一说法是不正确的，因此，不幸的是，该方法不是策略不变的。我们从理论和经验上证实了我们的发现。然后，我们通过导出校正项来对该方法进行修正，并表明该结果在理论上是正确的，并且在经验上是不变的。然而，我们的实证分析表明，修正后的DPBA不能加速提供有用建议的RL agent的学习。
我们介绍了一种简单的算法——策略不变显式塑形(policy invariant explicit shaping，PIES) ，证明了 PIES 能够支持任意的建议，具有策略不变性，并且能够加速 RL agent的学习。在学习开始时，当agent最需要指导时，PIES 会使agent的策略偏向于建议。随着时间的推移，PIES 会逐渐将这种偏差降低到零，从而确保策略的不变性。若干实验证实，当建议具有误导性时，PIES 能确保收敛到最优策略，当建议有用时，PIES 还能加速学习。
具体而言，本文作出了以下贡献:

1. （1） 识别已发布的奖励塑形方法中的一个重要缺陷。
2. （2） 从经验和理论上验证缺陷的存在。
3. （3） 对该方法进行了修正，但经验表明，它引入了额外的复杂性，好的建议不再提高学习速度。
4. （4） 介绍并验证了一种实现原始方法目标的简单方法。

2. BACKGROUND

----马尔可夫决策过程（MDP）[14]由元组描述$⟨S,A,T,\gamma ,R⟩$. 在每个时间步，环境都处于状态s∈S，agent采取行动a∈A，环境根据转移概率$T(s，a，s^{\prime })=Pr(s^{\prime }|s,a)$转变到新的状态$s^{\prime }\in S$。此外，agent（在每个时间步）根据奖励函数$R(s,a)$接收在状态s中采取动作a的奖励。最后，$\gamma$是折扣因子，指定如何权衡未来奖励和当前奖励。
----确定性策略$\pi$是从状态到动作的映射，$\pi ：S\to A$，也就是说，对于每个状态$s$，$\pi (s)$返回一个动作$a=\pi (s)$。状态-动作价值函数$Q_{\pi }(s,a)$定义为智能体在状态 s 中采取动作 $a$ 并随后遵循策略$\pi$将获得的折扣奖励的预期总和。

agent旨在找到由${\pi }^{\ast }$表示的最优策略，它使折扣奖励的期望总和最大化，与 ${\pi }^{\ast }$ 相关的状态-动作值函数称为最优状态-动作值函数，记为 $Q^{\ast }(s,a)$：
--------------------------------$Q^{\ast }(s,a)={\max }_{\pi \in \Pi }{Q}^{\pi }(s,a)$

其中， $\Pi$是所有策略的空间。
给定策略 $\pi$ 的动作价值函数满足贝尔曼方程：
---------------------------------$Q^{\pi }(s,a)=R(s,a)+\gamma {\Sigma }_{s^{\prime },a^{\prime }}[Q^{\pi }(s^{\prime },a^{\prime })]$
其中 $s^{\prime }$ 是下一个时间步的状态，$a^{\prime }$ 是agent在下一个时间步采取的动作，这对所有策略都是正确的。
最优策略 ${\pi }^{\ast }$的贝尔曼方程称为贝尔曼最优方程：
---------------------------$Q^{\ast }(s,a)=R(s,a)+\gamma {\Sigma }_{s^{\prime },a^{\prime }}[Q^{\ast }(s^{\prime },a^{\prime })]$
给定最优值函数 ${\pi }^{\ast }(s,a)$，agent可以通过对最优值函数的贪婪行动来检索最优策略：
-----------------------------${\pi }^{\ast }(s,a)={\max }_{a\in A}{Q}^{\ast }(s,a)$
许多强化学习算法背后的想法是迭代地学习最优值函数 $Q^{\ast }$。 例如，Sarsa [17] 在每个时间步 $t$使用以下更新规则学习 $Q$ 值（$Q_0$ 可以任意初始化）：
--------------------------------$Q_{t+1}(s_t,a_t)=Q_t(s_t,a_t)+{\alpha }_t{\delta }_t$ ------------------------------(1)
其中，
---------------------------${\delta }_t=R_t(s_t,a_t)+\gamma Q_t(s_{t+1},a_{t+1})-Q_t(s_t,a_t)$
是时间差误差（TD-error），$s_t$和 $a_t$ 表示时间步 $t$ 的状态和动作，$Q_t$ 表示时间步 $t$ 对 $Q^{\ast }$ 的估计，${\alpha }_t$是时间步 $t$的学习率。在某些条件下，保证这些 $Q$ 估计对于所有 $s$, $a$ 收敛到 $Q^{\ast }$，并且策略会收敛到$Q^{\ast }$ [17]。

PS：sarsa算法伪代码

2.1 Potential-Based Reward Shaping

----在奖励稀疏的情况下，奖励塑形可以通过提供额外的塑形奖励F来帮助agent更快地学习。然而，添加任意奖励可能会改变给定MDP的最优策略[15]。基于势能的奖励塑形 (Potential-based reward shaping，PBRS) 解决了将塑形奖励函数 $F$ 添加到现有 MDP 奖励函数R的问题，而无需通过将$F$定义为当前状态 $s$ 和下一个状态$s^{\prime }$的势能之差来更改最优策略[12]。具体而言，PBRS将塑形奖励限制为以下形式：$F(s,s^{\prime }):=\gamma \Phi (s^{\prime })-\Phi (s)$，其中$\Phi :s\to R$是势函数。Ng等人[12]表明，将$F$表示为势差是agent策略不变的充分条件。也就是说，如果原始MDP $⟨S,A,T,\gamma ,R⟩$ 表示为 $M$，塑形MDP $⟨S,A,T,\gamma ,R+F⟩$ 表示为$M^{\prime }$ ($M^{\prime }$与$M$相同，但除了$R$之外，还为agent提供了额外的奖励F)，则$M$和$M^{\prime }$对于任何状态-动作对$(s,a)$的最优值函数满足：
-------------------------------------------$Q_{M^{\prime }}^{\ast }=Q_M^{\ast }-\Phi (s)$
其中$\Phi$是偏置项。鉴于 $Q_{M^{\prime }}^{\ast }$, 最优策略${\pi }^{\ast }$ 可以简单地通过将偏置项相加为：
-----------------------------${\pi }^{\ast }(s,a)=arg{\max }_{a\in A}{Q}_M^{\ast }(s,a)=arg{\max }_{a\in A}(Q_{M^{\prime }}^{\ast }(s,a)+\Phi (s))$
由于偏差项仅取决于代理的状态，因此塑形MDP M′的最优策略与原始MDP M的最优策略没有区别。为了还包括对动作的塑形奖励，Wiewiora等人[20]将$F$的定义扩展为状态动作对，将$F$定义为：$F(s,a,s^{\prime },a^{\prime }):=\gamma \Phi (s^{\prime },a^{\prime })-\Phi (s,a)$ ，其中$\Phi$取决于agent状态和动作。现在，偏差项也取决于在状态$s$下采取的行动，因此,为了成为策略不变量, agent必须遵守策略
-----------------------------${\pi }^{\ast }(s,a)=arg{\max }_{a\in A}(Q_{M^{\prime }}^{\ast }(s,a)+\Phi (s))$

2.2 Dynamic Potential-Based Shaping

----如第 2.1 节所述，PBRS 仅限于可以用势能函数表示的外部建议。因此，它不满足三个目标中的第一个； 即，它不能接受任意建议。寻找一个准确捕捉建议的势能函数 $\Phi$ 可能具有挑战性。为了允许专家指定任意函数 $R^{expert}$ 并且仍然保持 PBRS 的所有属性，可以考虑动态 PBRS。
----动态PBRS使用可在线改变的势函数Φt来形成动态塑形奖励$F_t$，其中下标$t$表示$F$和$\Phi$变化的时间。Devlin和Kudenko[5]使用动态PBRS作为$F_{t+1}(s,s^{\prime }):=\gamma {\Phi }_{t+1}(s^{\prime })-{\Phi }_t(s)$，其中$t$和$t+1$分别是agent到达状态$s$和$s^{\prime }$的时间。他们为动态PBRS导出了与静态PBRS相同的策略不变性保证。为了承认一个任意的奖励，Harutyunyan等人[8]提出学习一个动态势函数${\Phi }_t$，给出一个任意有界函数$R^{expert}$ 形式的外部建议。为此，提出了以下名为基于动态势的建议（DPBA）的方法：定义$R^{\Phi }:=R^{expert}$，并在每个时间步通过以下更新规则学习二次值函数$\Phi$：
----------------${\Phi }_{t+1}(s,a):={\Phi }_t(s,a)+\beta {\delta }_t^{\Phi }$-------------------(2)

其中${\Phi }_t(s,a)$是$\Phi$的当前估计，$\beta$是$\Phi$函数的学习率，以及
----------------${\delta }_t^{\Phi }=R^{\Phi }(s,a)+\gamma {\Phi }_{t+1}(s^{\prime },a^{\prime })-{\Phi }_t(s,a)$
是$\Phi$函数的TD误差。一直以来，agent使用Sarsa学习$Q$值（即，根据等式1）。除了原始奖励$R(s,a)$之外，agent还接收塑形奖励，其给出如下：
-----------------------------------------$F_{t+1}(s,a,s^{\prime },a^{\prime }):={\Phi }_{t+1}(s^{\prime },a^{\prime })-{\Phi }_t(s,a)$-----------------(3)
也就是说，连续更新的 $\Phi$ 值之间的差。
Harutyunyan等人[8]建议，通过这种形式的奖励塑形，对于每个$s$和$a$ ,$Q_M^{\ast }(s,a)=Q_{M^{\prime }}^{\ast }(s,a)+{\Phi }_0(s,a)$，因此获得最优策略${\pi }^{\ast }$, agent应根据以下规则对$Q_{M^{\prime }}^{\ast }(s,a)+{\Phi }_0(s,a)$使用贪婪策略提取动作：

因此，如果${\Phi }_0(s,a)$被初始化为零，则等式4中的上述有偏策略将减少为原始的贪婪策略：

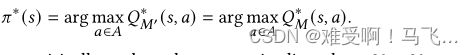
----DPBA在两个情景任务上进行了经验评估：一个20×20网格世界和一个推车杆问题。在网格世界实验中，agent从左上角开始每一集，直到到达位于右下角的目标，最多10000步。agent可以沿着四个基本方向移动，状态是agent的坐标$(s,a)$。到达目标状态时奖励函数为+1，其他位置为0。任何状态-行动的建议$R^{expert}$是：

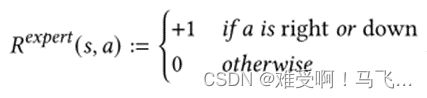
----本文在我们后面的实验中复制了相同的网格世界环境。
----在车杆任务[11]中，目标是尽可能长地平衡车顶上的一根杆子。购物车可以沿着轨道移动，每一集都从轨道中间开始，杆子竖直。有两种可能的操作: 对购物车施加 1或 -1的力。这种状态由一个四维连续向量组成，表示杆子的角度和角速度，以及推车的位置和速度。当杆子平衡了200步或者杆子倒下时，一集就结束了，奖励函数鼓励agent人平衡杆子。
----为了复制这个实验2，本文使用了OpenAI健身房[2]实现（cartpole-v0）3。这个任务的建议定义为：

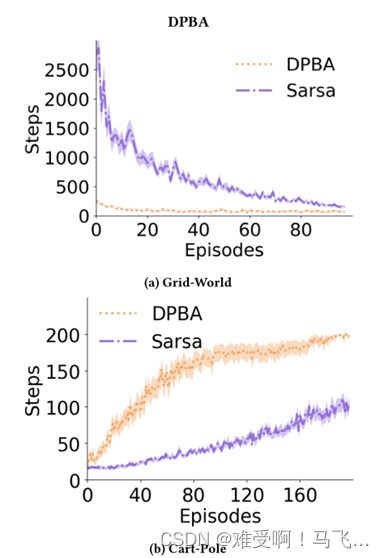
图1：y轴显示了在（a）50次和（b）30次跑步中平均完成每集（在x轴上）所用的时间步数。在a）网格世界和b）车极域中，将具有DPBA的成形agent与没有成形的Sarsa学习器进行比较。阴影区域对应于标准误差。

其中$o:S\times A\to 0，1$是一个函数，当杆方向与施加到推车上的力对齐时触发（即，当推车在杆倾斜的方向上移动时，agent将获得奖励）。我们设置$c=0.1$。
----图1显示了DPBA方法的性能，与没有收到任何专家建议的简单Sarsa学习器相比，DPBA方法在网格世界和推车杆域中的性能。我们使用了与[8]中用于网格世界相同的一组超参数。为了学习cart-pole任务，agent使用线性函数近似，通过Sarsa(λ)和瓦片编码特征表示[16]估计值函数，并使用开源软件（可在Richard Suttons的网站上公开）实现。Q和Φ的权重在0和0.001之间均匀随机初始化。对于瓦片编码，我们使用8个瓦片，每个瓦片有24个瓦片（每个维度2个）。为了更精确的状态表示，我们使用了一个包裹瓦片来表示极的角度。使用包裹瓦片，可以在一个范围内（例如[0, 2π]）进行概括，而不是将瓦片拉伸到无穷大，然后再包裹。λ设置为0.9，γ设置为1。对于Q和Φ值函数α和β的学习率，我们扫描了这些值[0.001, 0.002, 0.01, 0.1, 0.2]。根据图1(b)每条线的曲线下面积（AUC），最佳参数值如表1所示。
----这些结果与之前的研究结果一致，表明使用 DPBA 方法的agent对这个好的建议学习得更快，相对于不使用建议(即 DPBA 线收敛得更快，达到最优行为)。请注意，在网格世界的任务中，期望的行为是尽可能快地达到目标。因此，对于这个任务，在显示步骤(y 轴)和情节(x 轴)的情节(如图1中的情节)中，越低越好。相比之下，推车杆任务中目标的本质要求在每个阶段采取尽可能多的步骤，作为期望的行为。因此，对于推车杆高的情况，在同样轴线的情况下，效果更好。图1中的结果表明，DPBA 方法满足标准1(它可以使用任意奖励)和标准3(好的建议可以提高性能)。然而，正如我们在下一节中所讨论的，原始论文证明中的一个缺陷意味着准则2不能满足: 最优策略可以改变，也就是说，建议可以导致agent人收敛到次优策略。这在原始论文中没有经过实证检验，因此这种失败没有被注意到。

3. DPBA 会影响最优政策

上一节描述了DPBA，这是一种方法，可以通过迭代学习势函数$\Phi$并与塑形状态-动作值$Q_{M\prime }$同时学习，将任意专家的建议纳入强化学习框架。Harutyunyan等人[8]声称，如果$\Phi$，${\Phi }_0$的初始值被初始化为零，则agent可以简单地遵循相对于Q_{M′}贪婪的策略以实现策略不变性。在本节中，我们证明了这一说法不幸不成立：将${\Phi }_0(s,a)$初始化为零不足以保证策略不变性。

-------------为了证明我们的主张，我们从定义术语开始。我们将比较两个MDP中给定策略$\pi$的Q值估计，原始MDP由元组描述的$M$表示$⟨S、A、T、\gamma 、R⟩$, 以及由DPBA成形的MDP，$M^{\prime }$, 由元组描述$⟨S,A,T,\gamma ,R+F_{t+1}⟩$, 其中$F_{t+1}(s,a,s^{\prime },a^{\prime }):={\Phi }_{t+1}(s^{\prime },a^{\prime })-{\Phi }_t(s,a)$


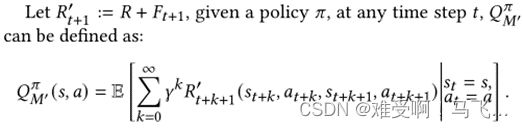
------无限求和中的两个项看起来非常相似，这促使我们通过移位求和变量k来重写其中一个项。这种移位将使相同的项被抵消。然而，我们需要小心。首先，我们重写极限形式的和。无限和可以写成：

在等式7中，如果$Q_t^{\pi }(s,a)$是有界的，那么当W接近无穷大时，极限内的第一项将变为0，而第二项不依赖于W，可以拉到极限外：

3.1 经验验证：无用的建议

----我们通过一系列实验验证了上述结果。首先，考虑一个确定性的2 × 2网格世界，我们称之为玩具示例，如图2所示。agent从状态 S 开始每一集，并且可以沿着四个基本方向移动(如图所示) ，直到达到目标状态 G (最多100步)。向墙移动(用粗线表示)不会改变agent的位置。除了在目标状态结束的一个转换之外，每个转换的奖励都是0，结果奖励 1和剧集终止。作为建议，我们假设“专家”奖励agent人偏离目标的转变。图2（a）中网格内的蓝色箭头表示专家建议的状态转换。代理通过执行建议的转换从专家处获得+1。由于该建议鼓励不良行为，我们预计它会减慢学习速度（而不是加快学习速度），但如果一种成形方法是策略不变的，则代理最终仍应收敛到最优策略。
----学习器使用Sarsa(0)估计Q值，γ=0.3。我们使用$ϵ-greedy$策略，对具有校正DPBA的学习者（等式9）和具有DPBA的学生（等式4）进行了实验。$\Phi$和$Q$被初始化为0，$ϵ$从0.1衰减为0。对于$Q$和$\Phi$值函数$\alpha$和$\beta$的学习率，我们扫描了值[0.05、0.1、0.2、0.5]。根据每条线的AUC，最佳值报告在表2中。图3将每集的长度描述为完成该集所需的步骤数。Sarsa线表示没有整形的Sarsa(0) agent的学习曲线。图3显示了DPBA没有收敛到带有错误建议的最优策略。该图还证实了我们的结果，即${\Phi }_t$（而不是Harutyunyan等人[8]中提出的${\Phi }_0$）是充分的校正项，以恢复最大化MDP原始奖励的最优策略。最后，我们验证了这不仅仅是agent开发过快的产物，并针对不同的开发速率重复相同的实验。我们考虑了另外两个不同的初始勘探率值，即0.3和0.5。
----图3中的相应行证实了额外的探索不会让DPBA获得最佳策略。图3还证实了等式9中导出的修正策略收敛于最优策略，即使专家建议不好。

3.2 经验验证: 有用的建议

----上一节表明，DPBA不是一种策略不变的塑形方法，因为将$\Phi$值初始化为零不是策略不变的充分条件。我们表明，DPBA可以通过添加正确的偏差项和策略不变量来校正。虽然添加正确的偏差项保证了策略的不变性，但我们仍然需要测试期望的奖励成形算法的第三个标准-校正后的DPBA是否能够在良好的专家建议下加速成形agent的学习？
----图4显示了与前一小节重复相同实验的结果，但是与图2(b)所示的优秀专家一起(即，从每个状态，专家鼓励agent朝着目标前进)。在这里，由于专家鼓励agent朝着目标前进，我们期望塑形agent比没有得到塑形奖励的agent学得更快。但是，图4显示了更正后的agent不能通过好的建议更快地学习。
----出乎我们意料的是，该建议实际上减缓了学习速度，尽管纠正后的DPBA agent最终如预期那样发现了最佳策略。要解释校正后的DPBA行为，需要仔细观察$Q$和$\Phi$估计值是如何变化的。校正后的DPBA在每个时间步加上$\Phi$的最新值，以校正塑形的$Q$值；然而，先前用于塑形奖励函数的$\Phi$值可能与最新值不同。让我们考虑$\Phi$已初始化为零的情况，建议总是一个积极的信号，强制$\Phi$值为负。对于这样的$\Phi$值，最新的Φ值比用于塑形奖励的早期值更负，这实际上阻碍了期望的行为。
----虽然校正后的DPBA保证了策略的不变性，但它无法满足理想奖励塑形的第三个目标（即，通过有用的建议加快agent的学习）。
----本节的主要结论是，上述用于纳入专家建议的奖励塑形方法均不满足三个理想目标。[8]中提出的DPBA可以导致更快的学习，如果专家提供了好的建议，但它不是策略不变的。本节中提出的修正DPBA是可证明的策略不变的，但即使提供了良好的建议，它也会导致学习速度减慢。

4. 策略不变显式塑形POLICY INVARIANT EXPLICIT SHAPING

----在这一部分中，我们介绍了满足我们在第1节中指定的所有奖励塑形目标的策略不变显式塑形(policy invariant explicit shaping，PIES)算法。PIES 是一个简单的算法，它可以接受任意的建议，具有策略不变性，并且可以根据专家的建议加快agent的学习速度。与基于势能的奖励塑形不同，PIES背后的主要思想是明确使用专家建议，而不修改原始奖励函数。不改变奖励函数是简化PIES并使分析其工作方式更容易的主要特征。PIES agent学习等式(1)中的原始值函数$Q_M$，同时学习等式(2)中基于专家建议的二次值函数$\Phi$。为了利用任意建议，agent通过在每个时间步 t 将 $-\Phi$ 添加到 $Q_M$ 显式地使agent的策略偏向于建议，并且通过参数${\xi }_t$加权，其中${\xi }_t$在学习结束之前衰减为0。
--------------------------------$Q_{t+1}(s_t,a_t)=Q_t(s_t,a_t)+{\alpha }_t{\delta }_t$ ------------------------------(1)
---------------------------------${\Phi }_{t+1}(s,a):={\Phi }_t(s,a)+\beta {\delta }_t^{\Phi }$-------------------(2)
例如，对于配备PIES的Sarsa(0) agent，当agent想要贪婪地行动时，它将在每个时间步选择使 最大化的动作。最佳策略是：

参数${\xi }_t$控制agent当前的动作在多大程度上偏向于建议。随着时间的推移，将${\xi }_t$衰减为0将消除塑形的影响，从而保证agent将收敛到最优策略，使PIES策略保持不变。衰减$\xi$的速度决定了建议将持续多久影响agent的学习策略。选择$\xi$的衰减速度可以与利用建议的益处有关，并且可以通过许多不同的方式来实现。对于本文，我们只在每一集结束时以线性状态减小 。更具体地说，第e集期间的$\xi$值为：

其中 $C$ 是一个常数，它决定了$\xi$衰减的速度； 即，$C$ 越大，偏差衰减越慢。
我们首先通过经验证明 PIES 实现了玩具示例中的所有三个目标。然后，我们将展示在提供良好建议的情况下，它如何针对网格世界中以前的方法和购物车杆问题(最初针对 DPBA 进行了测试)执行。所有域的规范都和以前一样。图5中玩具示例中agent的表现图显示了校正后的DPBA、PIES和Sarsa学习者的学习曲线。图5(a)是针对2(a)中所示的坏专家，图5(b)是针对2中所示的好专家。Sarsa(0)用于估计e=0.3和e-贪婪策略的状态动作值。$\Phi$和$Q$被初始化为0，e从0.1衰减为0。对于$Q$和$\Phi$值函数α和β的学习率，我们扫描了值[0.05、0.1、0.2、0.5]。设置$C$的研究值为[5，10，20，50]。值得一提的是，我们根据建议的质量设置了 的衰减速度（通过设置$C$）；例如，坏建议的$C$值越小越好，因为它会更快地衰减对抗性偏见的影响，而好建议的$C$越大越好，因为这会减缓衰减。根据每条线的AUC，使用最佳值。学习参数如表3所示。

正如预期的那样，使用 PIES，即使是坏专家，agent也能够找到最优策略。对于有益的建议，PIES 使agent能够更快地学习任务。然而，在玩具问题上，速度的加快并不显著，因为简单的学习者也能够在很少的情节中学习。
图6更好地展示了 PIES 如何通过在两个更复杂的任务中提供良好的建议来提高agent学习的性能: 网格世界和购物车-极点域，这在2.2节中有描述。对于这两个任务，相似的学习参数(那些我们没有重新状态的)继承了它们之前实验的值。为了找到最佳值，扫描了[50,100,200,300]的值。在 grid-world 任务(图6(a))中，并在值[0.05,0.1,0.2,0.5]上选择。在车杆任务(图6(b))中，为了设置学习率，扫描了[0.001,0.002,0.01,0.1,0.2]的值。与以前一样，图6(a)和6(b)的每一行的 AUC 值为最佳参数值，分别在表4和表5中报告。与前面一样，对于购物车杆任务的绘图，上面的线表示性能更好，而对于网格世界，下面的线表示性能更好。
PIES在两个领域都正确地使用了好的建议，并在不改变最优策略的情况下改进了对Sarsa学习者的学习（即PIES以比Sarsa学生更快的速度接近最优行为）。PIES的表现比纠正的DPBA好，正如预期的那样，因为纠正后的DPBA不能用好的建议加速学习者。当我们有任意形式的建议时，无论建议的质量如何，PIES都是DPBA的可靠替代方案。如图所示，PIES满足所有三个所需标准。