知识图谱论文梳理【TransR:用于知识图完成的学习实体和关系嵌入】
系列文章目录
知识图谱论文梳理【 HyTE:基于超平面的时序知识图谱】
知识图谱论文梳理【 TransE:】
知识图谱论文梳理【 TransH:】
知识图谱论文梳理【 TransR:】
知识图谱论文梳理【 TransD:】
知识图谱论文梳理【 TransA:】
知识图谱论文梳理【 TransG:】
知识图谱论文梳理【 Transparse:】
知识图谱论文梳理【 TransA+:】
Learning Entity and Relation Embeddings for Knowledge Graph Completion
Yankai Lin1, Zhiyuan Liu1∗, Maosong Sun1,2, Yang Liu3, Xuan Zhu3 1 Department of Computer Science and Technology, State Key Lab on Intelligent Technology and Systems, National Lab for Information Science and Technology, Tsinghua University, Beijing, China 2 Jiangsu Collaborative Innovation Center for Language Competence, Jiangsu, China 3 Samsung R&D Institute of China, Beijing, China
文章目录
- 系列文章目录
- Learning Entity and Relation Embeddings for Knowledge Graph Completion
- Abstract
- 摘要
- 一、介绍
- 二、相关模型
-
- 1、TransE and TransH
- 2、其他模型
-
-
- 非结构化模型 (UM)
- 结构化嵌入 (SE)
- 单层模型 (SLM)
- 语义匹配引擎(SME)
- 潜在因子模型(LFM)
- 神经张量网络 (NTN)
-
- 3、我们的模型
-
-
- TransR
-
- 4、基于聚类的 TransR (CTransR)
- 5、训练方法和实施细节
- 三、实验与分析
-
- 1、数据集和实验设置
- 2、链接预测
- 3、三元组分类
- 4、从文本中提取关系
- 四、结论和未来工作
-
-
- Acknowledgments
- 参考文献
-
Abstract
Knowledge graph completion aims to perform link prediction between entities. In this paper, we consider the approach of knowledge graph embeddings. Recently, models such as TransE and TransH build entity and relation embeddings by regarding a relation as translation from head entity to tail entity. We note that these models simply put both entities and relations within the same semantic space. In fact, an entity may have multiple aspects and various relations may focus on different aspects of entities, which makes a common space insufficient for modeling. In this paper, we propose TransR to build entity and relation embeddings in separate entity space and relation spaces. Afterwards, we learn embeddings by first projecting entities from entity space to corresponding relation space and then building translations between projected entities. In experiments, we evaluate our models on three tasks including link prediction, triple classification and relational fact extraction. Experimental results show significant and consistent improvements compared to stateof-the-art baselines including TransE and TransH. The source code of this paper can be obtained from https: //github.com/mrlyk423/relation extraction.
摘要
知识图谱完成旨在执行实体之间的链接预测。在本文中,我们研究了知识图谱嵌入的方法。最近,像TransE和TransH这样的模型通过将关系视为从头部实体到尾部实体的转换来构建实体和关系嵌入。我们注意到,这些模型只是将实体和关系放在同一个语义空间中。事实上,一个实体可能有多个方面,各种关系可能集中在实体的不同方面,这使得公共空间不足以进行建模。在本文中,我们提出TransR在单独的实体空间和关系空间中构建实体和关系嵌入。之后,我们通过首先将实体从实体空间投影到相应的关系空间,然后在投影实体之间构建转换来学习嵌入。在实验中,我们通过三个任务评估我们的模型,包括链接预测,三重分类和关系事实提取。实验结果表明,与包括TransE和TransH在内的最先进的基线相比,显着且一致的改善。本文的源代码可以从https://github.com/mrlyk423/relation 提取中获得。
一、介绍
知识图对实体的结构化信息及其丰富的关系进行编码。尽管一个典型的知识图谱可能包含数百万个实体和数十亿个关系事实,但它通常还很不完整。知识图谱补全旨在在现有知识图谱的监督下预测实体之间的关系。知识图谱补全可以发现新的关系事实,是对纯文本关系抽取的重要补充。
知识图谱完成与社交网络分析中的链接预测类似,但更具挑战性,原因如下:(1)知识图中的节点是具有不同类型和属性的实体;(2)知识图谱中的边缘是不同类型的关系。对于知识图谱完成,我们不仅要确定两个实体之间是否存在关系,还要预测关系的具体类型。
因此,传统的链路预测方法无法完成知识图谱。最近,该任务的一种有前途的方法是将知识图谱嵌入到连续的向量空间中,同时保留图的某些信息。按照这种方法,已经探索了许多方法,这些方法将在“相关工作”一节中详细介绍。
在这些方法中,TransE (Bordes et al. 2013) 和 TransH (Wang et al. 2014) 简单有效,实现了最先进的预测性能。 TransE 受 (Mikolov et al. 2013b) 的启发,学习实体和关系的向量嵌入。这些向量嵌入在 R k R^k Rk 中设置,我们用相同的粗体字母表示。 TransE 背后的基本思想是,两个实体之间的关系对应于实体嵌入之间的转换,即当 (h, r, t) 成立时,h + r ≈ t。由于 TransE 在建模 1-to-N、N-to-1 和 N-to-N 关系时存在问题,因此提出 TransH 以使实体在涉及各种关系时具有不同的表示。
TransE和TransH都假设实体和关系的嵌入位于同一空间 R k R^k Rk中。但是,一个实体可能具有多个方面,并且各种关系都集中在实体的不同方面。因此,直观地说,一些实体在实体空间中是相似的,因此彼此接近,但在某些特定方面却相对不同,因此在相应的关系空间中彼此相距甚远。为了解决这个问题,我们提出了一种新方法,该方法对不同空间中的实体和关系进行建模,即实体空间和多关系空间(即特定于关系的实体空间),并在相应的关系空间中执行转换,因此称为TransR。
TransR的基本思想如图1所示。对于每个三元组(h,r,t),实体空间中的实体首先以 h r h_r hr和 t r t_r tr的形式投影到r关系空间中,运算Mr,然后hr + r≈tr。特定于关系的投影可以使实际保持关系(表示为彩色圆圈)的头/尾实体彼此靠近,并且还可以远离那些不保持关系的实体(表示为彩色三角形)。
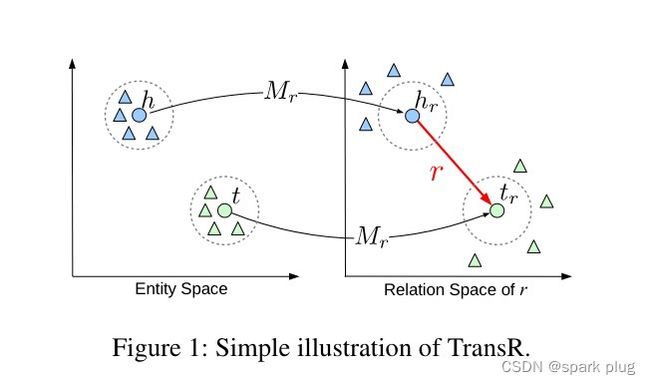
此外,在特定关系下,头尾实体对 通常表现出不同的模式。仅构建单个关系向量来执行从头实体到尾实体的所有转换是不够的。例如,关系“位置位置包含”的头尾实体具有许多模式,例如国家/地区-城市、国家/地区-大学、大陆-国家/地区等。遵循分段线性回归的思想(Ritzema等人1994),我们通过将不同的头尾实体对聚类成组并为每个组学习不同的关系向量来扩展TransR,称为基于簇的TransR(CTransR)。我们通过WordNet和Freebase的基准数据集上的链接预测,三元组分类和关系事实提取任务来评估我们的模型。实验结果表明,与最先进的模型相比,实验结果显著且一致。
二、相关模型
1、TransE and TransH
如“简介”部分所述,当 (h, r, t) 成立时,TransE (Bordes et al. 2013) 希望 h + r ≈ t h+r ≈ t h+r≈t。这表明 (t) 应该是 (h + r) 的最近邻。因此,TransE 假设评分函数在 ( h , r , t ) (h, r, t) (h,r,t) 成立时为低,否则为高。
f r ( h , t ) = ‖ h + r − t ‖ 2 2 f_r(h, t) = ‖h + r − t‖_2^2 fr(h,t)=‖h+r−t‖22
TransE适用于1对1关系,但对N-to-1、1-to-N 和 N-to-N 关系有问题。以 1-to-N 关系 r 为例。 ∀ i ∈ 0 , . . . , m , ( h i , r , t ) ∈ S ∀i ∈ {0, . . . , m}, (hi, r, t) ∈ S ∀i∈0,...,m,(hi,r,t)∈S.这表明 h 0 = . . . = h m , h_0 = . . . = h_m, h0=...=hm,这与事实不符。
为了解决建模 N-to-1、1-to-N 和 N-to-N 关系时的 TransE 问题,TransH (Wang et al. 2014) 被提议使实体在涉及不同的关系。对于关系 r,TransH 将关系建模为超平面上的向量 r,其中 wr 作为法线向量。对于三元组 (h, r, t),实体嵌入 h 和 t 首先投影到 wr 的超平面,表示为 h⊥ 和 t⊥。然后将打分函数定义为:
f r ( h , t ) = ‖ h ⊥ + r − t ⊥ ‖ 2 2 . f_r(h, t) = ‖h_⊥ + r − t_⊥‖_2^2. fr(h,t)=‖h⊥+r−t⊥‖22.
如果我们限制 ‖ w r ‖ 2 = 1 ‖w_r‖_2 = 1 ‖wr‖2=1,我们将得到 h ⊥ = h − w r T h w r h_⊥ = h − w_r^T hw_r h⊥=h−wrThwr和 t ⊥ = t − w r T t w r t_⊥ = t−w^T_r tw_r t⊥=t−wrTtwr。通过将实体嵌入投影到关系超平面中,它允许实体在不同的关系中扮演不同的角色。
2、其他模型
除了 TransE 和 TransH 之外,还有许多其他方法遵循知识图嵌入的方法。在这里,我们介绍了几个典型的模型,也将在实验中与我们的模型进行比较作为基线。
非结构化模型 (UM)
UM模型(Bordes et al. 2012; 2014)被提议作为TransE的朴素版本,通过分配所有r = 0,导致得分函数 f r ( h , t ) = ‖ h − t ‖ 2 2 f_r(h,t) = ‖h − t‖_2^2 fr(h,t)=‖h−t‖22。该模型无法考虑关系的差异。
结构化嵌入 (SE)
SE模型(Bordes et al. 2011)为头部和尾部实体设计了两个特定于关系的矩阵,即Mr,1和Mr,2,并将分数函数定义为两个投影向量之间的L1距离,即 f r ( h , t ) = ‖ M r , 1 h − M r , 2 t ‖ 1 f_r(h,t)= ‖M_r,_1h − M_r,_2t‖_1 fr(h,t)=‖Mr,1h−Mr,2t‖1。由于模型具有两个单独的优化矩阵,因此它无法捕获实体和关系之间的精确关系。
单层模型 (SLM)
SLM模型被提出作为NTN的幼稚基线(Socher等人,2013)。SLM模型的评分函数定义为
f r ( h , t ) = u r T g ( M r , 1 h + M r , 2 t ) , fr(h, t) = u^T_r g(M_r,_1h + M_r,_2t), fr(h,t)=urTg(Mr,1h+Mr,2t),
其中 Mr,1 和 Mr,2 是权重矩阵,g() 是 tanh 运算。SLM 是 NTN 的一个特例,当 NTN 中的张量设置为 0 时。
语义匹配引擎(SME)
SME模型(Bordes et al. 2012; 2014)旨在通过多个矩阵产品和Hadamard产品捕获实体和关系之间的相关性。SME模型仅使用单个向量表示每个关系,该向量通过线性矩阵积与实体向量进行交互,所有关系共享相同的参数。SME考虑了语义匹配能量函数的两种定义进行优化,包括线性形式
f r ( h , t ) = ( M 1 h + M 2 r + b 1 ) T ( M 3 t + M 4 r + b 2 ) f_r(h, t) = (M_1h + M_2r + b_1)^T(M_3t + M_4r + b_2) fr(h,t)=(M1h+M2r+b1)T(M3t+M4r+b2)
和双线性形式
f r ( h , t ) = ( ( M 1 h ) ⊗ ( M 2 r ) + b 1 ) T ( ( M 3 t ) ⊗ ( M 4 r ) + b 2 ) f_r(h, t) = ((M_1h)⊗(M_2r)+b_1 )^T((M_3t)⊗(M_4r)+b_2 ) fr(h,t)=((M1h)⊗(M2r)+b1)T((M3t)⊗(M4r)+b2)
其中 M1、M2、M3 和 M4 是权重矩阵,⊗ 是 Hadamard 积,b1 和 b2 是偏置向量。在 (Bordes et al. 2014) 中,SME 的双线性形式是用三向张量而不是矩阵重新定义的。
潜在因子模型(LFM)
LFM模型(Jenatton et al. 2012;Sutskever,Tenenbaum和Salakhutdinov 2009)使用二次形式考虑实体嵌入之间的二阶相关性,并定义了双线性评分函数 f r ( h , t ) = h T M r t 。 f_r(h,t) = h^TM_rt。 fr(h,t)=hTMrt。
神经张量网络 (NTN)
NTN 模型 (Socher et al. 2013) 为图嵌入定义了一个表达得分函数,如下所示,
f r ( h , t ) = u r T g ( h T M r t + M r , 1 h + M r , 2 t + b r ) , f_r(h, t) = u^T_r g(h^TM_rt + M_r,_1h + M_r,_2t + b_r), fr(h,t)=urTg(hTMrt+Mr,1h+Mr,2t+br),
其中,u 是特定于关系的线性层,g() 是 tanh 运算,Mr. ∈ Rd×d×k 是 3 元张量,Mr,1, Mr,2 ∈ Rk×d 是权重矩阵。同时,NTN相应的高复杂度可能会阻碍其在大规模知识图谱上的有效应用。在实验中,我们还将与RESCAL进行比较,RESCAL是一种集体矩阵分解模型(Nickel,Tresp和Kriegel 2011; 2012)。
3、我们的模型
为了解决 TransE 和 TransH 的表示问题,我们提出了 TransR,它表示由关系特定矩阵桥接的不同语义空间中的实体和关系。
TransR
TransE 和 TransH 都假设在同一空间 R k R^k Rk 中嵌入实体和关系。但是关系和实体是完全不同的对象,它可能无法在一个共同的语义空间中表示它们。尽管 TransH 通过使用关系超平面扩展了建模的灵活性,但它并没有完美地打破这个假设的限制。为了解决这个问题,我们提出了一种新方法,它在不同的空间(即实体空间和关系空间)中对实体和关系进行建模,并在关系空间中进行翻译,因此被命名为 TransR。
在 TransR 中,对于每个三元组(h、r、t),实体嵌入被设置为 h 、 t ∈ R k h、t ∈ R^k h、t∈Rk,关系嵌入被设置为 r ∈ R d . r∈R^d. r∈Rd. 请注意,实体嵌入和关系嵌入的维度不一定相同,即 k ≠ d k \neq d k=d。
对于每个关系 r,我们设置一个投影矩阵 M r ∈ R k × d M_r ∈ R^{k×d} Mr∈Rk×d,它可以将实体从实体空间投影到关系空间。使用映射矩阵,我们将实体的投影向量定义为
h r = h M r , t r = t M r . h_r = hM_r, t_r = tM_r. hr=hMr,tr=tMr.
评分函数相应地定义为
f r ( h , t ) = ‖ h r + r − t r ‖ 2 2 . f_r(h, t) = ‖h_r + r − t_r‖_2^2. fr(h,t)=‖hr+r−tr‖22.
在实践中,我们对嵌入 h、r、t 和映射矩阵的规范(即 ∀h、r、t)强制实施约束,我们有 ‖ h ‖ 2 ≤ 1 , ‖ r ‖ 2 ≤ 1 , ‖ t ‖ 2 ≤ 1 , ‖ h M r ‖ 2 ≤ 1 , ‖ t M r ‖ 2 ≤ 1 。 ‖h‖_2 ≤ 1,‖r‖_2 ≤ 1,‖t‖_2 ≤ 1,‖hM_r‖_2 ≤ 1,‖tM_r‖_2 ≤ 1。 ‖h‖2≤1,‖r‖2≤1,‖t‖2≤1,‖hMr‖2≤1,‖tMr‖2≤1。
4、基于聚类的 TransR (CTransR)
上面提到的模型,包括 TransE、TransH 和 TransR,为每个关系学习一个唯一的向量,因为这些关系通常是相当多样化的,所以它可能无法代表该关系下的所有实体对。为了更好地模拟这些关系,我们结合了分段线性回归的思想(Ritzema 等 1994)来扩展 TransR。
基本思想是,我们首先将输入实例分成几组。形式上,对于特定关系 r,训练数据中的所有实体对 (h, t) 都聚类为多个组,并且每个组中的实体对应表现出相似的 r 关系。所有实体对(h,t)都用它们的向量偏移(h − t)表示以进行聚类,其中h和t是用TransE获得的。之后,我们分别为每个集群学习一个单独的关系向量 rc,为每个关系学习矩阵 Mr。我们将实体的投影向量定义为 h r , c = h M r 和 t r , c = t M r , h_r,_c = hM_r 和 t_r,_c = tM_r, hr,c=hMr和tr,c=tMr,评分函数定义为
f r ( h , t ) = ‖ h r , c + r c − t r , c ‖ 2 2 + α ‖ r c − r ‖ 2 2 , f_r(h, t) = ‖h_r,_c + r_c − t_r,_c‖^2_2 + α‖r_c − r‖^2_2, fr(h,t)=‖hr,c+rc−tr,c‖22+α‖rc−r‖22,
其中 ‖ r c − r ‖ 2 2 ‖r_c − r‖^2_2 ‖rc−r‖22 旨在确保集群特定的关系向量 r c r_c rc 离原始关系向量 r r r 不太远,并且 α α α控制此约束的效果。此外,与TransR一样,CTransR还对嵌入h,r,t和映射矩阵的范数施加约束。
5、训练方法和实施细节
我们将以下基于边缘打分函数定义为训练目标
L = ∑ ( h , r , t ) ∈ S ∑ ( h ′ , r , t ′ ) ∈ S ′ m a x ( 0 , f r ( h , t ) + γ − f r ( h ′ , t ′ ) ) , L= ∑ _{(h,r,t)∈S} ∑ _{(h^′ ,r,t^′ )∈S^′} max (0, f_r(h, t) + γ − f_r(h^′, t^′)), L=(h,r,t)∈S∑(h′,r,t′)∈S′∑max(0,fr(h,t)+γ−fr(h′,t′)),
其中 m a x ( x , y ) max(x, y) max(x,y) 旨在获得 x 和 y 之间的最大值, γ γ γ是边距,S 是正确三元组的集合,S′ 是不正确的三元组的集合。
现有的知识图谱只包含正确的三元组。通过替换实体来破坏正确的三元组 ( h , r , t ) ∈ S , (h,r,t)∈S, (h,r,t)∈S,并构造不正确的三元组 ( h ′ , r , t ′ ) ∈ S ′ (h',r,t')∈S^′ (h′,r,t′)∈S′是例行公事。当破坏三元组时,我们遵循(Wang等人,2014)并为头/尾实体替换分配不同的概率。对于那些1到N,N到1和N到N的关系,通过给予更多机会来替换“一方”,生成假阴性实例的机会将减少。在实验中,我们将传统的采样方法表示为“unif”,并将(Wang et al. 2014)中的新方法表示为“bern”。
TransR 和 CTransR 的学习过程是使用随机梯度下降 (SGD) 进行的。为了避免过度拟合,我们使用 TransE 的结果初始化实体和关系嵌入,并将关系矩阵初始化为单位矩阵。
三、实验与分析
1、数据集和实验设置
在本文中,我们使用两个典型的知识图谱来评估我们的方法,这两个图谱是用WordNet(Miller 1995)和Freebase(Bollacker et al. 2008)构建的。WordNet提供单词的语义知识。在 WordNet 中,每个实体都是一个由多个单词组成的 synset,对应于一个不同的单词意义。在表示其词法关系的合成集之间定义关系,例如超名词、催眠、meronym 和 holonym。在本文中,我们使用了来自WordNet的两个数据集,即(Bordes et al. 2014)中使用的WN18和(Socher et al. 2013)中使用的WN11。WN18 包含 18 种关系类型,WN11 包含 11 种关系类型。Freebase提供了世界的一般事实。例如,三重(史蒂夫·乔布斯,创立,苹果公司)在名称实体史蒂夫·乔布斯和组织实体苹果公司之间建立了一种关系。在本文中,我们使用了Freebase的两个数据集,即用于(Bordes et al. 2014)的FB15K和用于(Socher et al. 2013)的FB13。我们在表 1 中列出了这些数据集的统计信息。
Table 1: Statistics of data sets.
| Dataset | #Rel | #Ent | #Train | #Valid | # Test |
|---|---|---|---|---|---|
| WN18 | 18 | 40,943 | 141,442 | 5,000 | 5,000 |
| FB15K | 1,345 | 14,951 | 483,142 | 50,000 | 59,071 |
| WN11 | 11 | 38,696 | 112,581 | 2,609 | 10,544 |
| FB13 | 13 | 75,043 | 316,232 | 5,908 | 23,733 |
| FB40K | 1,336 | 39528 | 370,648 | 67,946 | 96,678 |
2、链接预测
链接预测旨在预测关系事实三元组(h,r,t)的缺失h或t,被用于(Bordes et al. 2011; 2012; 2013)。在此任务中,对于缺失实体的每个位置,要求系统从知识图谱中对一组候选实体进行排名,而不是仅给出一个最佳结果。如(Bordes et al. 2011; 2013)所述,我们使用数据集WN18和FB15K进行实验。
在测试阶段,对于每个测试三元组(h,r,t),我们将头/尾实体替换为知识图中的所有实体,并按分数函数fr计算的相似性分数的降序对这些实体进行排名。下面(Bordes et al. 2013),我们使用两个度量作为我们的评估指标:(1)正确实体的平均等级;(2)排名前10位的实体中正确实体的比例(Hits@10)。良好的链接预测变量应达到较低的平均秩或较高的Hits@10。事实上,知识图谱中也可能存在损坏的三元组,这也应该被认为是正确的。但是,上述评估可能会低估那些将这些损坏但正确的系统列为三倍高的系统。因此,在排名之前,我们可以过滤掉这些出现在知识图谱中的损坏的三元组。我们将第一个评估设置命名为“Raw”,将后一个评估设置命名为“过滤器”。
由于我们使用相同的数据集,因此我们将模型与(Bordes et al. 2013;王等人,2014)。对于 TransR 和 CTransR 的实验,我们在 {0.1, 0.01, 0.001} 中选择 SGD 的学习速率 λ,在 {1, 2, 4} 中选取边距γ,在 {20, 50, 100} 中选择实体嵌入 k 和关系嵌入 d 的维度,在 {0.1, 0.01, 0.001} 中选择 CTransR 的批大小 B 在 {20, 120, 480, 1440, 4800} 和 α之间。最佳配置是根据验证集中的平均排名确定的。最优构型为λ = 0.001,γ = 4,k = 50,d = 50,B = 1440,α = 0.001,并将L1作为WN18上的相似性;λ = 0.001,γ = 1,k = 50,d = 50,B = 4800,α = 0.01,并将L1作为FB15K上的相似性。对于这两个数据集,我们遍历所有训练三元组 500 轮。
WN18和FB15K的评估结果如表2所示。从表中我们观察到:(1)TransR和CTransR明显且一致地优于其他基线方法,包括TransE和TransH。这表明TransR在模型复杂性和表现力之间找到了更好的权衡。(2)CTransR的性能优于TransR,这表明我们应该构建细粒度模型来处理每种关系类型下的复杂内部相关性。CTransR是初步的探索;为此目的,我们未来的工作将是建立更复杂的模型。(3)“bern”采样技巧适用于TransH和TransR,特别是在具有更多关系类型的FB15K上。
在表3中,我们通过映射FB15K上关系1的属性来显示单独的评估结果。我们可以看到TransR在所有映射关系类别上都取得了很大的改进,特别是当(1)预测“1对1”关系时,这表明TransR为实体和关系及其复杂相关性提供了更精确的表示,如图1所示;(2)预测“1对N”和“N对1”关系的1边,这表明TransR通过关系特异性投影区分相关实体和不相关实体的能力。
表 4:〈头、尾部〉一些集群关于“位置位置包含”的关系的例子。
| 〈Head, Tail〉 | |
|---|---|
| 1 | 〈Africa, Congo〉, 〈Asia, Nepal〉, 〈Americas, Aruba〉, 〈Oceania, Federated States of Micronesia〉 |
| 2 | 〈United States of America, Kankakee〉, 〈England, Bury St Edmunds〉, 〈England, Darlington〉, 〈Italy, Perugia〉 |
| 3 | 〈Georgia, Chatham County〉, 〈Idaho, Boise〉, 〈Iowa, Polk County〉, 〈Missouri, Jackson County〉, 〈Nebraska, Cass County〉 |
| 4 | 〈Sweden, Lund University〉, 〈England, King’s College at Cambridge〉, 〈Fresno, California State University at Fresno〉, 〈Italy, Milan Conservatory〉 |
表 4 给出了 FB15K 训练三元组中“位置位置包含”关系的一些群集示例。我们可以找到明显的模式:集群#1是关于包含国家的大陆,集群#2是关于包含城市的国家,集群#3是关于包含县的州,集群#4是关于包含大学的国家。很明显,通过聚类,我们可以学习更精确和细粒度的关系嵌入,这可以进一步帮助提高知识图谱完成的性能。
3、三元组分类
三元分类旨在判断给定的三元组 (h, r, t) 是否正确。这是一个二元分类任务,已在 (Socher et al. 2013; Wang et al. 2014) 中进行了探索以进行评估。在此任务中,我们使用三个数据集 WN11、FB13 和 FB15K,如下 (Wang et al. 2014),其中前两个数据集用于 (Socher et al. 2013)。
我们需要负三元组来评估二元分类。 NTN (Socher et al. 2013) 发布的数据集 WN11 和 FB13 已经有负三元组,它们是通过破坏正确的三元组获得的。由于之前的工作没有发布带有负三元组的 FB15K,我们按照 (Socher et al. 2013) 中的相同设置构建负三元组。对于三重分类,我们设置了关系特定阈值 δr。对于一个三元组(h,r,t),如果fr得到的相异度分数低于δr,则三元组将被分类为正,否则为负。通过最大化验证集上的分类准确度来优化 δr。
对于 WN11 和 FB13,我们将我们的模型与使用相同数据集的 (Wang et al. 2014) 中报告的基线方法进行比较。正如 (Wang et al. 2014) 中提到的,为了公平比较,所有报告的结果都没有与词嵌入结合。
由于 FB15K 是我们自己根据 (Socher et al. 2013) 中的策略生成的,因此评估结果无法直接与 (Wang et al. 2014) 中报道的结果进行比较。因此,我们实现 TransE 和 TransH,并使用 (Socher et al. 2013) 发布的 NTN 代码,并在我们的 FB15K 数据集上进行评估以进行比较。
对于 TransR 的实验,我们在 {0.1, 0.01, 0.001, 0.0001} 中选择 SGD 的学习率 λ,在 {1, 2, 4} 中选择边距 γ,实体嵌入的维度 k,在 {20, 50 中的关系嵌入 d, 100} 和批量大小 B 在 {20, 120, 480, 960, 4800} 中。根据验证集的准确率确定最佳配置。最佳配置为:λ=0.001,γ=4,k,d=20,B=120,以L1为WN11上的相异度; λ = 0.0001,γ = 2,k,d = 100 和 B = 480,并将 L1 作为 FB13 上的相异性。对于这两个数据集,我们遍历所有训练三元组 1000 轮。
三重分类的评价结果如表5所示。从表 5 中,我们观察到:(1)在 WN11 上,TransR 显着优于包括 TransE 和 TransH 在内的基线方法。 (2) 在 FB13 上,TransE、TransH 和 TransR 都不能胜过最具表现力的模型 NTN。相比之下,在更大的数据集 FB15K 上,TransE、TransH 和 TransR 的表现要好于 NTN。结果可能与数据集的特征相关:FB15K 中有 1、345 种关系类型,而 FB13 中只有 13 种关系类型。同时,两个数据集中的实体和关系事实的数量接近。正如 (Wang et al. 2014) 中所讨论的,FB13 中的知识图比 FB15K 甚至 WN11 密集得多。似乎最具表现力的模型 NTN 可以使用 FB13 的密集图的张量变换来学习复杂的相关性。相比之下,更简单的模型能够以良好的泛化能力更好地处理 FB15K 的稀疏图。 (3) 此外,“bern”采样技术提高了 TransE、TransH 和 TransR 在所有三个数据集上的性能。
如 (Wang et al. 2014) 所示,TransE 和 TransH 的训练时间分别约为 5 分钟和 30 分钟。 TransR 的计算复杂度高于 TransE 和 TransH,训练时间约为 3 小时。
表 5:三重分类的评估结果。 (%)
| Data Sets | WN11 | FB13 | FB15K |
|---|---|---|---|
| SE | 53.0 | 75.2 | - |
| SME (bilinear) | 70.0 | 63.7 | - |
| SLM | 69.9 | 85.3 | - |
| LFM | 73.8 | 84.3 | - |
| NTN | 70.4 | 87.1 | 68.5 |
| TransE (unif) | 75.9 | 70.9 | 79.6 |
| TransE (bern) | 75.9 | 81.5 | 79.2 |
| TransH (unif) | 77.7 | 76.5 | 79.0 |
| TransH (bern) | 78.8 | 83.3 | 80.2 |
| TransR (unif) | 85.5 | 74.7 | 81.7 |
| TransR (bern) | 85.9 | 82.5 | 83.9 |
| CTransR (bern) | 85.7 | - | 84.5 |
4、从文本中提取关系
关系抽取旨在从大规模纯文本中提取关系事实,这是丰富知识图谱的重要信息来源。大多数现有方法(Mintz et al. 2009; Riedel, Yao, and McCallum 2010; Hoffmann et al. 2011; Surdeanu et al. 2012)将知识图谱作为远程监督,以自动注释大规模文本语料库中的句子作为训练实例,然后提取文本特征来构建关系分类器。这些方法只使用纯文本来推理新的关系事实;同时,知识图嵌入仅基于现有知识图执行链接预测。
利用纯文本和知识图来推断新的关系事实很简单。在 (Weston et al. 2013) 中,TransE 和基于文本的提取模型相结合,对候选事实进行排序,并取得了可喜的改进。在 TransH 上也发现了类似的改进(Wang et al. 2014)。在本节中,我们将研究 TransR 在结合基于文本的关系提取模型时的性能。
我们采用 NYT+FB,也用于 (Weston et al. 2013),构建基于文本的关系提取模型。在这个数据集中,纽约时报语料库中的实体用斯坦福 NER 注释并链接到 Freebase。
在我们的实验中,我们实现了 (Weston et al. 2013) 中提出的相同的基于文本的提取模型,称为 Sm2r。对于知识图谱部分,(Weston et al. 2013) 使用了一个子集,限制在前 400 万个实体中,有 23000 种关系类型。由于 TransH 尚未发布数据集,并且 TransR 从 400 万个实体中学习需要太长时间,我们自己生成了一个较小的数据集 FB40K,其中包含 NYT 中的所有实体和 1、336 种关系类型。为了测试的公平性,我们从 FB40K 中删除了所有实体对出现在 NYT 测试集中的三元组。与 (Weston et al. 2013; Wang et al. 2014) 中的先前结果相比,我们发现使用 FB40K 学习不会显着降低 TransE 和 TransH 的有效性。因此,我们可以安全地使用 FB40K 来证明 TransR 的有效性。
按照 (Weston et al. 2013) 中的相同方法,我们将基于文本的关系提取模型的分数与知识图嵌入的分数相结合,对测试三元组进行排序,得到 TransE、TransH 和 TransR 的精确召回曲线。由于我们数据集的 freebase 部分是我们自己构建的,与 (Wang et al. 2014) 中的不同,评估结果不能直接与 (Wang et al. 2014) 中报告的结果进行比较。因此,我们自己实现 TransE、TransH 和 TransR。我们设置嵌入维度 k,d = 50,学习率 λ = 0.001,余量 γ = 1.0,B = 960,相异性度量为 L1。评价曲线如图2所示。
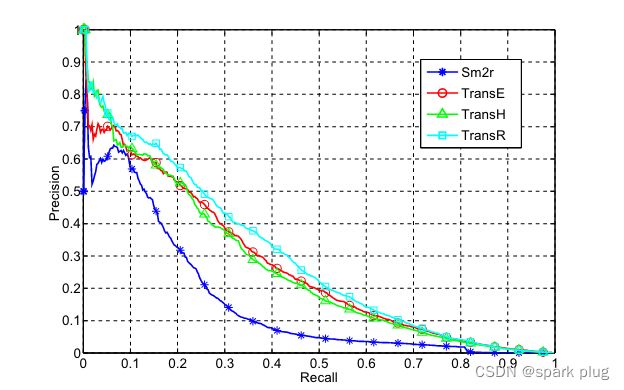
图 2:用于从文本中提取关系的 TransE、TransH 和 TransR 的精确召回曲线。
从表中我们观察到 TransR 在召回范围 [0, 0.05] 时优于 TransE 并且与 TransH 相当,并且在召回范围 [0.05, 1] 时优于包括 TransE 和 TransH 在内的所有基线。最近,嵌入的概念也被广泛用于表示单词和文本(Bengio et al. 2003; Mikolov et al. 2013a; 2013b; Mikolov, Yih, and Zweig 2013),可用于基于文本的关系提取.
四、结论和未来工作
在本文中,我们提出了一种新的知识图嵌入模型 TransR。 TransR 将实体和关系嵌入到不同的实体空间和关系空间中,并通过投影实体之间的翻译来学习嵌入。此外,我们还提出了 CTransR,旨在基于分段线性回归的思想对每种关系类型内的内部复杂相关性进行建模。在实验中,我们在三个任务上评估我们的模型,包括链接预测、三重分类和从文本中提取事实。实验结果表明,与 TransE 和 TransH 相比,TransR 实现了一致且显着的改进。
我们将探索以下进一步的工作:
- 包括 TransR 在内的现有模型分别考虑每个关系事实。事实上,关系以丰富的模式相互关联。例如,如果我们知道 (goldfish, kind of, fish) 和 (fish, kind of, animal),我们可以推断 (goldfish, kind of, animal),因为关系类型 kind of 是可传递的。我们可以利用这些关系模式来进行知识图嵌入。
- 在从文本中提取关系事实时,我们简单地执行线性加权平均来结合文本侧提取模型和知识图嵌入模型的分数。未来,我们可能会探索文本端和知识图谱的统一嵌入模型。
- CTransR 是对每种关系类型内的内部相关性进行建模的初步探索。将来,我们将为此目的研究更复杂的模型。
Acknowledgments
这项工作得到了 973 计划 (No. 2014CB340501)、国家自然科学基金 (NSFC No. 61133012 和 61202140) 和清华-三星联合实验室的支持。我们感谢所有匿名审稿人的建设性意见。
参考文献
Bengio, Y.; Ducharme, R.; Vincent, P.; and Jauvin, C. 2003. A neural probabilistic language model. JMLR 3:1137–1155.
Bollacker, K.; Evans, C.; Paritosh, P.; Sturge, T.; and Taylor, J. 2008. Freebase: a collaboratively created graph database for structuring human knowledge. In Proceedings of KDD, 1247–1250.
Bordes, A.; Weston, J.; Collobert, R.; Bengio, Y.; et al. 2011. Learning structured embeddings of knowledge bases. In Proceedings of AAAI, 301–306.
Bordes, A.; Glorot, X.; Weston, J.; and Bengio, Y. 2012. Joint learning of words and meaning representations for open-text semantic parsing. In Proceedings of AISTATS, 127–135. Bordes, A.; Usunier, N.; Garcia-Duran, A.; Weston, J.; and Yakhnenko, O. 2013. Translating embeddings for modeling multi-relational data. In Proceedings of NIPS, 2787–2795.
Bordes, A.; Glorot, X.; Weston, J.; and Bengio, Y. 2014. A semantic matching energy function for learning with multirelational data. Machine Learning 94(2):233–259.
Hoffmann, R.; Zhang, C.; Ling, X.; Zettlemoyer, L.; and Weld, D. S. 2011. Knowledge-based weak supervision for information extraction of overlapping relations. In Proceedings of ACL-HLT, 541–550.
Jenatton, R.; Roux, N. L.; Bordes, A.; and Obozinski, G. R. 2012. A latent factor model for highly multi-relational data. In Proceedings of NIPS, 3167–3175.
Mikolov, T.; Chen, K.; Corrado, G.; and Dean, J. 2013a. Efficient estimation of word representations in vector space. Proceedings of ICLR.
Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G. S.; and Dean, J. 2013b. Distributed representations of words and phrases and their compositionality. In Proceedings of NIPS, 3111–3119.
Mikolov, T.; Yih, W.-t.; and Zweig, G. 2013. Linguistic regularities in continuous space word representations. In Proceedings of HLT-NAACL, 746–751.
Miller, G. A. 1995. Wordnet: a lexical database for english. Communications of the ACM 38(11):39–41.
Mintz, M.; Bills, S.; Snow, R.; and Jurafsky, D. 2009. Distant supervision for relation extraction without labeled data. In Proceedings of ACL-IJCNLP, 1003–1011.
Nickel, M.; Tresp, V.; and Kriegel, H.-P. 2011. A threeway model for collective learning on multi-relational data. In Proceedings of ICML, 809–816.
Nickel, M.; Tresp, V.; and Kriegel, H.-P. 2012. Factorizing yago: scalable machine learning for linked data. In Proceedings of WWW, 271–280.
Riedel, S.; Yao, L.; and McCallum, A. 2010. Modeling relations and their mentions without labeled text. In Machine Learning and Knowledge Discovery in Databases. 148–163. Ritzema, H., et al. 1994. Drainage principles and applications. Socher, R.; Chen, D.; Manning, C. D.; and Ng, A. 2013. Reasoning with neural tensor networks for knowledge base completion. In Proceedings of NIPS, 926–934.
Surdeanu, M.; Tibshirani, J.; Nallapati, R.; and Manning, C. D. 2012. Multi-instance multi-label learning for relation extraction. In Proceedings of EMNLP, 455–465.
Sutskever, I.; Tenenbaum, J. B.; and Salakhutdinov, R. 2009. Modelling relational data using bayesian clustered tensor factorization. In Proceedings of NIPS, 1821–1828.
Wang, Z.; Zhang, J.; Feng, J.; and Chen, Z. 2014. Knowledge graph embedding by translating on hyperplanes. In Proceedings of AAAI, 1112–1119.
Weston, J.; Bordes, A.; Yakhnenko, O.; and Usunier, N. 2013. Connecting language and knowledge bases with embedding models for relation extraction. In Proceedings of EMNLP, 1366–1371.