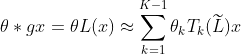GCN论文阅读与代码梳理(2)——STGCN
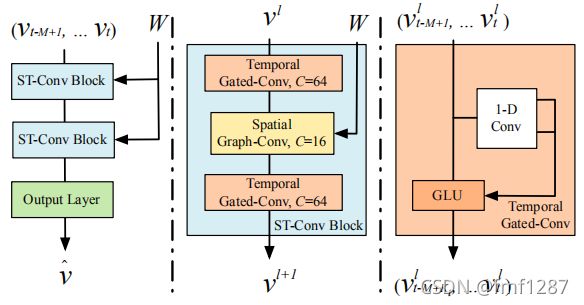
本文提出了基于时空图卷积的网络,解决交通流量预测问题(中长期流量预测问题)。
STGCN包含两个时空卷积核和一个输出层。
时空卷积核包含一个时域门控卷积、一个空域门控卷积和一个时域门控卷积。
-
整体时空卷积核的代码如下:
注意到,第一个时域卷积核的激活函数为GLU,而空域卷积核和第二个时域卷积核的激活函数为relu。
def st_conv_block(x, Ks, Kt, channels, scope, keep_prob, act_func='GLU'):
'''
Spatio-temporal convolutional block, which contains two temporal gated convolution layers
and one spatial graph convolution layer in the middle.
:param x: tensor, batch_size, time_step, n_route, c_in].
:param Ks: int, kernel size of spatial convolution.
:param Kt: int, kernel size of temporal convolution.
:param channels: list, channel configs of a single st_conv block.
:param scope: str, variable scope.
:param keep_prob: placeholder, prob of dropout.
:param act_func: str, activation function.
:return: tensor, [batch_size, time_step, n_route, c_out].
'''
c_si, c_t, c_oo = channels
with tf.variable_scope(f'stn_block_{scope}_in'):
x_s = temporal_conv_layer(x, Kt, c_si, c_t, act_func=act_func)
x_t = spatio_conv_layer(x_s, Ks, c_t, c_t)
with tf.variable_scope(f'stn_block_{scope}_out'):
x_o = temporal_conv_layer(x_t, Kt, c_t, c_oo)
print('*********************** st_conv_block x_o shape: ', x_o.shape)
x_ln = layer_norm(x_o, f'layer_norm_{scope}')
print('*********************** st_conv_block x_ln shape: ', x_ln.shape)
return tf.nn.dropout(x_ln, keep_prob)-
时域门控卷积沿着时间对输入做一维卷积
GLU门控单元在Language model with gated convolutional network中被提出,可以有效降低CNN的梯度弥散问题,同时保留非线性能力。公式如下,相当于对(X*W+b)中的信息进行筛选:
![]()
在STGCN代码中,将参数W和b初始化为2*c_out的向量与输入x_input相乘并进行一维时间卷积得到x_conv,将x_conv前c_out与输入x_input相加,将x_conv后c_out送入sigmoid与前者相乘,即完成了GLU门控操作。
相应代码如下:
def temporal_conv_layer(x, Kt, c_in, c_out, act_func='relu'):
'''
Temporal convolution layer.
:param x: tensor, [batch_size, time_step, n_route, c_in].
:param Kt: int, kernel size of temporal convolution.
:param c_in: int, size of input channel.
:param c_out: int, size of output channel.
:param act_func: str, activation function.
:return: tensor, [batch_size, time_step-Kt+1, n_route, c_out].
'''
print("$$$$$$$$$$$$$$$$$$$$ c_in:", c_in)
print("$$$$$$$$$$$$$$$$$$$$ c_out:", c_out)
_, T, n, _ = x.get_shape().as_list()
if c_in > c_out:
w_input = tf.get_variable('wt_input', shape=[1, 1, c_in, c_out], dtype=tf.float32)
tf.add_to_collection(name='weight_decay', value=tf.nn.l2_loss(w_input))
x_input = tf.nn.conv2d(x, w_input, strides=[1, 1, 1, 1], padding='SAME') # 卷积操作
elif c_in < c_out:
# if the size of input channel is less than the output,
# padding x to the same size of output channel.
# Note, _.get_shape() cannot convert a partially known TensorShape to a Tensor.
x_input = tf.concat([x, tf.zeros([tf.shape(x)[0], T, n, c_out - c_in])], axis=3)
else:
x_input = x
print("$$$$$$$$$$$$$$$$$$$$ X SHAPE:", x.shape)
# keep the original input for residual connection.
x_input = x_input[:, Kt - 1:T, :, :]
if act_func == 'GLU':
# gated liner unit
wt = tf.get_variable(name='wt', shape=[Kt, 1, c_in, 2 * c_out], dtype=tf.float32)
tf.add_to_collection(name='weight_decay', value=tf.nn.l2_loss(wt))
bt = tf.get_variable(name='bt', initializer=tf.zeros([2 * c_out]), dtype=tf.float32)
x_conv = tf.nn.conv2d(x, wt, strides=[1, 1, 1, 1], padding='VALID') + bt
print('*********************** temporal_conv_layer x_conv shape: ', x_conv.shape)
# 残差连接,x_conv最后一维为 2 * c_out维度,前c_out与输入相加,后c_out送入sigmoid与前者相乘
return (x_conv[:, :, :, 0:c_out] + x_input) * tf.nn.sigmoid(x_conv[:, :, :, -c_out:])
else:
wt = tf.get_variable(name='wt', shape=[Kt, 1, c_in, c_out], dtype=tf.float32)
tf.add_to_collection(name='weight_decay', value=tf.nn.l2_loss(wt))
bt = tf.get_variable(name='bt', initializer=tf.zeros([c_out]), dtype=tf.float32)
x_conv = tf.nn.conv2d(x, wt, strides=[1, 1, 1, 1], padding='VALID') + bt
if act_func == 'linear':
return x_conv
elif act_func == 'sigmoid':
return tf.nn.sigmoid(x_conv)
elif act_func == 'relu':
return tf.nn.relu(x_conv + x_input)
else:
raise ValueError(f'ERROR: activation function "{act_func}" is not defined.')-
空域门控卷积
传统的卷积方法忽略了图的连通性和全局性,因此需要利用图卷积提取全局的图特征。由于基于傅里叶变换的图卷积有着 o(N^2)的时间复杂度,采用了两种估计方法解决复杂度问题:
1、切比雪夫多项式估计图卷积核如下,其中 T_k(\widetilde{L}) 为k阶切比雪夫多项式在归一化拉普拉斯矩阵上的值。
2、一阶估计。
![]()
同样采用了残差连接,利用gconv函数对输入x进行空域图卷积得到x_gc,再经过relu与x_input相加。
相应代码如下:
def gconv(x, theta, Ks, c_in, c_out):
"""
Spectral-based graph convolution function.
:param x: tensor, [batch_size, n_route, c_in].
:param theta: tensor, [Ks*c_in, c_out], trainable kernel parameters.
:param Ks: int, kernel size of graph convolution.
:param c_in: int, size of input channel.
:param c_out: int, size of output channel.
:return: tensor, [batch_size, n_route, c_out].
"""
# graph kernel: tensor, [n_route, Ks*n_route]
kernel = tf.get_collection('graph_kernel')[0]
n = tf.shape(kernel)[0]
x_tmp = tf.reshape(tf.transpose(x, [0, 2, 1]), [-1, n])
x_mul = tf.reshape(tf.matmul(x_tmp, kernel), [-1, c_in, Ks, n])
x_ker = tf.reshape(tf.transpose(x_mul, [0, 3, 1, 2]), [-1, c_in * Ks])
# x_gconv -> [batch_size*n_route, c_out] -> [batch_size, n_route, c_out]
x_gconv = tf.reshape(tf.matmul(x_ker, theta), [-1, n, c_out])
return x_gconv
def spatio_conv_layer(x, Ks, c_in, c_out):
'''
Spatial graph convolution layer.
:param x: tensor, [batch_size, time_step, n_route, c_in].
:param Ks: int, kernel size of spatial convolution.
:param c_in: int, size of input channel.
:param c_out: int, size of output channel.
:return: tensor, [batch_size, time_step, n_route, c_out].
'''
_, T, n, _ = x.get_shape().as_list()
if c_in > c_out:
# bottleneck down-sampling
w_input = tf.get_variable('ws_input', shape=[1, 1, c_in, c_out], dtype=tf.float32)
tf.add_to_collection(name='weight_decay', value=tf.nn.l2_loss(w_input))
x_input = tf.nn.conv2d(x, w_input, strides=[1, 1, 1, 1], padding='SAME')
elif c_in < c_out:
# if the size of input channel is less than the output,
# padding x to the same size of output channel.
# Note, _.get_shape() cannot convert a partially known TensorShape to a Tensor.
x_input = tf.concat([x, tf.zeros([tf.shape(x)[0], T, n, c_out - c_in])], axis=3)
else:
x_input = x
ws = tf.get_variable(name='ws', shape=[Ks * c_in, c_out], dtype=tf.float32)
tf.add_to_collection(name='weight_decay', value=tf.nn.l2_loss(ws))
variable_summaries(ws, 'theta')
bs = tf.get_variable(name='bs', initializer=tf.zeros([c_out]), dtype=tf.float32)
# x -> [batch_size*time_step, n_route, c_in] -> [batch_size*time_step, n_route, c_out]
x_gconv = gconv(tf.reshape(x, [-1, n, c_in]), ws, Ks, c_in, c_out) + bs
print('*********************** spatio_conv_layer x_conv shape: ', x_gconv.shape)
# x_g -> [batch_size, time_step, n_route, c_out]
x_gc = tf.reshape(x_gconv, [-1, T, n, c_out])
print('*********************** spatio_conv_layer x_gc shape: ', x_gc.shape)
return tf.nn.relu(x_gc[:, :, :, 0:c_out] + x_input) # 残差连接