Sklearn
Sklearn
Sklearn就是一个处理特殊任务的包, 就是处理机器学习 (有监督学习和无监督学习) 的包,更精确的说,它里面有六个任务模块和一个数据引入模块:
- 有监督学习的分类任务
- 有监督学习的回归任务
- 无监督学习的聚类任务
- 无监督学习的降维任务
- 数据预处理任务
- 模型选择任务
- 数据引入
1 数据
1.1 数据格式
在 Sklean 里,模型能即用的数据有两种形式:
- Numpy 二维数组 (ndarray) 的稠密数据 (dense data),通常都是这种格式。
- SciPy矩阵 (scipy.sparse.matrix) 的稀疏数据 (sparse data),比如文本分析每个单词 (字典有 100000 个词) 做独热编码得到矩阵有很多 0,这时用 ndarray 就不合适了,太耗内存。
上述数据在机器学习中通常用符号 X 表示,是模型自变量。
它的大小 = [样本数, 特征数]。该房屋数据有 21000 条包括平方英尺,卧室数,楼层,日期,翻新年份等等 21 栏。该数据形状为 [21000, 21]
有监督学习除了需要特征 X 还需要标签 y,而 y 通常就是 Numpy 一维数组,无监督学习没有 y。
1.2 引入数据
Sklearn 三种引入数据形式:
- 打包好的数据:对于小数据集,用
sklearn.datasets.load_* - 分流下载数据:对于大数据集,用
sklearn.datasets.fetch_* - 随机创建数据:为了快速展示,用
sklearn.datasets.make_*
星号 * 是指的是具体文件名
Load 一个数字小数据集 digits
#Load 一个数字小数据集 digits
digits = datasets.load_digits()
digits.keys()
dict_keys(['data', 'target', 'target_names',
'images', 'DESCR'])
#Fetch 一个加州房屋大数据集 california_housing
california_housing = datasets.fetch_california_housing()
california_housing.keys()
dict_keys(['data', 'target',
'feature_names', 'DESCR'])
#Make 一个高斯分位数数据集 gaussian_quantile
gaussian_quantiles = datasets.make_gaussian_quantiles()
type(gaussian_quantiles), len(gaussian_quantiles)
(tuple, 2)
2 核心 API
Sklearn 里万物皆估计器。估计器是个非常抽象的叫法,可把它不严谨的当成一个模型 (用来回归、分类、聚类、降维),或当成一套流程 (预处理、网格最终)。
- 估计器 (estimator) 当然是估计器
- 预测器 (predictor) 是具有预测功能的估计器
- 转换器 (transformer) 是具有转换功能的估计器
3 估计器
定义:任何可以基于数据集对一些参数进行估计的对象都被称为估计器。
两个核心点:1. 需要输入数据,2. 可以估计参数。
估计器首先被创建,然后被拟合。
创建估计器:需要设置一组超参数,比如
- 线性回归里超参数 normalize=True
- K 均值里超参数 n_clusters=3
在创建好的估计器 model 可以直接访问这些超参数,用 . 符号。
- model.normalize
- model.n_clusters
拟合估计器:需要训练集。在有监督学习中的代码范式为
model.fit( X_train, y_train )
在无监督学习中的代码范式为
model.fit( X_train )
拟合之后可以访问 model 里学到的参数,比如线性回归里的特征前的系数 coef_,或 K 均值里聚类标签 labels_。
- model.coef_
- model.labels_
3.1 线性回归
首先从 sklearn 下的 linear_model 中引入 LinearRegression,再创建估计器起名 model,设置超参数 normalize 为 True,指的在每个特征值上做标准化,这样会加速数值运算。
from sklearn.linear_model import LinearRegression
model = LinearRegression(normalize=True)
model
![]()
创建完后的估计器会显示所有的超参数,比如我们设置好的 normalize=True,其他没设置的都是去默认值,比如 n_jobs=None 是只用一个核,你可以将其设为 2 就是两核并行,甚至设为 -1 就是电脑里所有核并行。
#创建一个简单数据集 (没有噪声完全线性)
x = np.arange(10)
y = 2 * x + 1
plt.plot( x, y, 'o' );
#例中 X 是一维,因为我们用 np.newaxis 加一个维度,它做的事情就是把 [1, 2, 3] 转成 [[1],[2],[3]]。再把 X 和 y 丢进 fit() 函数来拟合线性模型的参数。
X = x[:, np.newaxis]
model.fit( X, y )
#用「model.param_」可以访问到学好的参数了
print( model.coef_ )
print( model.intercept_ )
[2.]
1.0
斜率为 2,截距为 1。和访问超参数时不一样,注意访问参数要加一个下划线 _。
3.2 K 均值
首先从 sklearn 下的 cluster 中引入 KMeans,再创建估计器起名 model,设置超参数 n_cluster 为 3
from sklearn.cluster import KMeans
model = KMeans( n_clusters=3 )
model
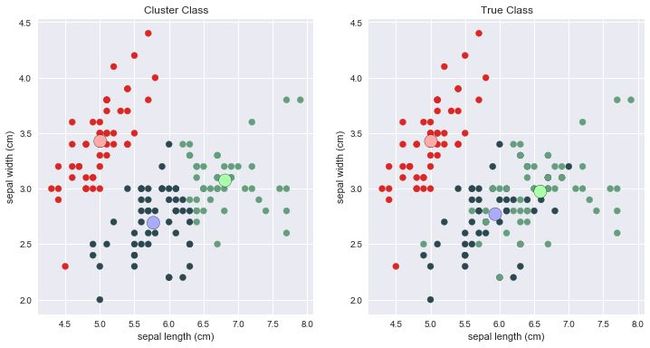
iris 里的特征有四个吗 (萼片长、萼片宽、花瓣长、花瓣宽)?四维特征很难可视化,因此我们只取两个特征 (萼片长、萼片宽) 来做聚类并且可视化结果。注意下面代码 X = iris.data[:,0:2]。
X = iris.data[:,0:2]
model.fit(X)
用「model.param_」可以访问到学好的参数了
print( model.cluster_centers_, '\n')
print( model.labels_, '\n' )
print( model.inertia_, '\n')
print( iris.target )
- model.cluster_centers_:簇中心。三个簇那么有三个坐标。
- model.labels_:聚类后的标签
- model.inertia_:所有点到对应的簇中心的距离平方和 (越小越好)
真实标签 iris.label 和聚类标签 model.labels_ 看起来差的很远。类别 0 都一致,但是类别 1 和 2 弄反了,这是因为在 KMeans 算法里标注的类别索引和真实类别索引不一样
上面以有监督学习的 LinearRegression 和无监督学习的 KMeans 举例,但实际上可以将它们替换成其他别的模型。
它们都是「估计器」,因此都有 fit() 方法。使用它们的通用伪代码如下:
# 有监督学习
from sklearn.xxx import SomeModel
# xxx 可以是 linear_model 或 ensemble 等
model = SomeModel( hyperparameter )
model.fit( X, y )
# 无监督学习
from sklearn.xxx import SomeModel
# xxx 可以是 cluster 或 decomposition 等
model = SomeModel( hyperparameter )
model.fit( X )
4 预测器
定义:预测器在估计器上做了一个延展,延展出预测的功能。
两个核心点:1. 基于学到的参数预测,2. 预测有很多指标。最常见的就是 predict() 函数:
- model.predict(X_test):评估模型在新数据上的表现
- model.predict(X_train):确认模型在老数据上的表现
首先将数据分成 80:20 的训练集 (X_train, y_train) 和测试集 (X_test, y_test),在用从训练集上拟合 fit() 的模型在测试集上预测 predict()。
from sklearn.datasets import load_iris
iris = load_iris()
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test
= train_test_split( iris['data'],
iris['target'],
test_size=0.2 )
print( 'The size of X_train is ', X_train.shape )
print( 'The size of y_train is ', y_train.shape )
print( 'The size of X_test is ', X_test.shape )
print( 'The size of y_test is ', y_test.shape )
4.1 对率回归
首先从 sklearn 下的 linear_model 中引入 LogisticRegression,再创建估计器起名 model,设置超参数 mutli_class 为 multinomial 因为有三种鸢尾花,是个多分类问题。
在训练集上拟合参数,这时估计器 model 里面已经可以访问这些参数了。
对于分类问题,我们不仅想知道预测的类别是什么,有时还想知道预测该类别的信心如何。前者用 predict(),后者用 predict_proba()。
在测试集上比较预测标签 y_pred 和真实标签 y_test 发现它们完全吻合,准确率 100%
y_pred = model.predict( X_test )
p_pred = model.predict_proba( X_test )
print( y_test, '\n' )
print( y_pred, '\n' )
print( p_pred )
p_pred - 测试集里有 30 个数据,鸢尾花有 3 类,因此 predict_proba() 生成一个 30×3 的数组,每行的概率加起来为 1。
把「每行中最大概率值对应的那一类」作为预测结果。
预测器里还有额外的两个函数可以使用。在分类问题中
- score() 返回的是分类准确率
- decision_function() 返回的是每个样例在每个类下的分数值
print( model.score( X_test, y_test ) )
print( np.sum(y_pred==y_test)/len(y_test) )
1.0
1.0
decision_score = model.decision_function( X_test )
print( decision_score )
把「每行中最高得分值对应的那一类」作为预测结果
4.2 K 均值
继续上一节的 KMeans 模型,首先用 fit() 训练。
再用 predict() 在测试集上预测出类别 inx_pred,和真实标签 y_test 比对。再次强调,inx_pred 和 y_test 给三个类别的索引定义是不同的。
idx_pred = model.predict( X_test[:,0:2] )
print( index_pred )
print( y_test )
使用它们的通用伪代码如下:
# 有监督学习
from sklearn.xxx import SomeModel
# xxx 可以是 linear_model 或 ensemble 等
model = SomeModel( hyperparameter )
model.fit( X, y )
y_pred = model.predict( X_new )
s = model.score( X_new )
# 无监督学习
from sklearn.xxx import SomeModel
# xxx 可以是 cluster 或 decomposition 等
model = SomeModel( hyperparameter )
model.fit( X )
idx_pred = model.predict( X_new )
s = model.score( X_new )
5 转换器
**定义:转换器也是一种估计器,两者都带拟合功能,但**估计器做完**拟合来预测,而*转换器做完*拟合来转换。
核心点:估计器里 fit + predict,转换器里 fit + transform。
两大类转换器
- 将分类型变量 (categorical) 编码成数值型变量 (numerical)
- 规范化 (normalize) 或标准化 (standardize) 数值型变量
LabelEncoder 和 OrdinalEncoder 都可以将字符转成数字,但是
- LabelEncoder 的输入是一维,比如 1d ndarray
- OrdinalEncoder 的输入是二维,比如 DataFrame
首先给出要编码的列表 enc 和要解码的列表 dec。
enc = ['win','draw','lose','win']
dec = ['draw','draw','win']
从 sklearn 下的 preprocessing 中引入 LabelEncoder,再创建转换器起名 LE,不需要设置任何超参数。
from sklearn.preprocessing import LabelEncoder
LE = LabelEncoder()
print( LE.fit(enc) )
print( LE.classes_ )
print( LE.transform(dec) )
LabelEncoder()
['draw' 'lose' 'win']
[0 0 2]
- 第 4 行转换器 fit 之后还是转换器,只不过从数据 enc 上学到了些东西
- 第 5 行的 LE.classes_ 就是学到的东西之一,系统把 ‘draw’, ‘lose’, ‘win’ 分别赋予 0, 1, 2
- 第 6 行用学到的东西来解码 [‘draw’,‘draw’,‘win’] 得到 [0 0 2]
上面这种编码的问题是,算法会认为两个临近的值比两个疏远的值要更相似。显然这样不对 (比如,0 和 1 比 0 和 2 距离更近,难道 draw 和 win 比 draw 和 lose更相似?)。
解决这个问题,一个常见的方法是给每个分类创建一个二元属性,即独热编码 (one-hot encoding)。
独热编码其实就是把一个整数用向量的形式表现。下图就是对数字 0-9 做独热编码。
转换器 OneHotEncoder 可以接受两种类型的输入:
- 用 LabelEncoder 编码好的一维数组
- DataFrame
一. 用 LabelEncoder 编码好的一维数组 (元素为整数),重塑 (用 reshape(-1,1)) 成二维数组作为 OneHotEncoder 输入。
from sklearn.preprocessing import OneHotEncoder
OHE = OneHotEncoder()
num = LE.fit_transform( enc )
print( num )
OHE_y = OHE.fit_transform( num.reshape(-1,1) )
OHE_y
[2 0 1 2]
<4x3 sparse matrix of type
''
with 4 stored elements
in Compressed Sparse Row format>
- 第 5 行打印出编码结果 [2 0 1 2]
- 第 6 行将其转成独热形式,输出是一个「稀疏矩阵」形式,因为实操中通常类别很多,因此就一步到位用稀疏矩阵来节省内存
想看该矩阵里具体内容,用 toarray() 函数。
OHE_y.toarray()
array([[0., 0., 1.],
[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
二. 用 DataFrame作为 OneHotEncoder 输入。
OHE = OneHotEncoder()
OHE.fit_transform( enc_DF ).toarray()
array([[0., 0., 1.],
[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
特征缩放
数据要做的最重要的转换之一是特征缩放 (feature scaling)。当输入的数值的量纲不同时,机器学习算法的性能都不会好。
具体来说,对于某个特征,我们有两种方法:
- 标准化 (standardization):每个维度的特征减去该特征均值,除以该维度的标准差
- 规范化 (normalization):每个维度的特征减去该特征最小值,除以该特征的最大值与最小值之差。
MinMaxScaler
from sklearn.preprocessing import MinMaxScaler
X = np.array( [0, 0.5, 1, 1.5, 2, 100] )
X_scale = MinMaxScaler().fit_transform( X.reshape(-1,1) )
X_scale
array([[0. ],
[0.005],
[0.01 ],
[0.015],
[0.02 ],
[1. ]])