原文来自CSDN,公众号ID:CSDNnews,对其结构略作改动。
- 1. 写在前面
2018 年 FIFA 世界杯即将拉开帷幕,全世界的球迷都热切地想要知道:谁将获得那梦寐以求的大力神杯?如果你不仅是个足球迷,而且也是高科技人员的话,我猜你肯定知道机器学习和人工智能也是目前的流行词。让我们结合两者来预测一下本届俄罗斯 FIFA 世界杯哪个国家将夺冠。
作者:Gerald Muriuki,经济、数据科学专家
译者:弯月,责编:郭芮
点击此处获取完整的代码:https://github.com/itsmuriuki/FIFA-2018-World-cup-predictions
- 2. 译文
足球比赛涉及的因素非常繁多,我无法将所有因素都融入机器学习模型中。本文只是一个黑客想用数据尝试一些很酷的东西。本文的目标是:
-
用机器学习来预测谁将赢得2018 FIFA世界杯的冠军;
-
预测整个比赛的小组赛结果;
-
模拟四分之一决赛、半决赛以及决赛。
这些目标代表了独一无二的现实世界里机器学习的预测问题,并将解决机器学习中的各种任务:数据集成、特征建模和结果预测。
- 2.1 数据:
我采用了两个来自 Kaggle 的数据集,我们将使用自 1930 年第一届世界杯以来所有参赛队的历史赛事结果。
FIFA 排名是于 90 年代创建的,因此这里缺失很大一部分数据,所以我们使用历史比赛记录。点击以下链接获取所有数据 :
- https://www.kaggle.com/martj42/international-football-results-from-1872-to-2017/data;
- 本文中主要使用的环境和工具有:jupyter notebook、numpy、pandas、seaborn、matplotlib 和 scikit-learn。
首先,我们要针对两个数据集做探索性分析,然后经过特征工程来选择与预测关联性最强的特征,还有数据处理,再选择一个机器学习模型,最后将模型配置到数据集上。
- 2.2 让我们开始动手吧:
首先,导入所需的代码库,并将数据集加载到数据框中:
1 import pandas as pd 2 import numpy as np 3 import matplotlib.pyplot as plt 4 import seaborn as sns 5 import matplotlib.ticker as ticker 6 import matplotlib.ticker as plticker 7 from sklearn.model_selection import train_test_split 8 from sklearn.linear_model import LogisticRegression
导入数据集:
1 #load data 2 world_cup = pd.read_csv('C:\Coding\FIFA2018-World-cup\datasets\World Cup 2018 Dataset.csv') 3 results = pd.read_csv('C:/Coding/FIFA2018-World-cup/datasets/results.csv')
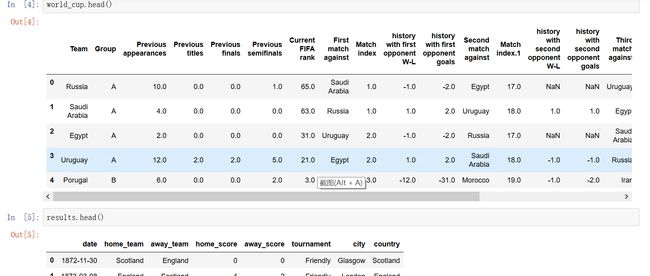
下一步是加载数据集。通过调用 world_cup.head() 和 results.head() ,务必将两个数据集都加载到数据框中,如下所示:
- 2.3 探索性分析:
在分析了两组数据集后,所得的数据集包含了以往赛事的数据——这个新的(所得的)数据集对于分析和预测将来的赛事非常有帮助。
探索性分析和特征工程:需要建立与机器学习模型相关的特征,在任何数据科学的项目中,这部分工作都是最耗时的。
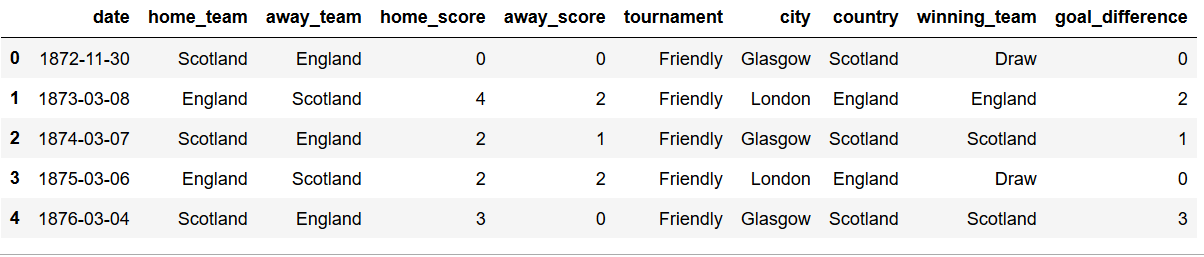
现在我们把目标差异和结果列添加到结果数据集:
1 #Adding goal difference and establishing who is the winner 2 winner = [] 3 for i in range (len(results['home_team'])): 4 if results ['home_score'][i] > results['away_score'][i]: 5 winner.append(results['home_team'][i]) 6 elif results['home_score'][i] < results ['away_score'][i]: 7 winner.append(results['away_team'][i]) 8 else: 9 winner.append('Draw') 10 results['winning_team'] = winner 11 12 #adding goal difference column 13 results['goal_difference'] = np.absolute(results['home_score'] - results['away_score']) 14 15 results.head()
检查一下新的结果数据框:
然后我们着手处理仅包含尼日利亚参加比赛的一组数据(这可以帮助我们集中找出哪些特征对一个国家有效,随后再扩展到参与世界杯的所有国家):
1 #lets work with a subset of the data one that includes games played by Nigeria in a Nigeria dataframe 2 df = results[(results['home_team'] == 'Nigeria') | (results['away_team'] == 'Nigeria')] 3 nigeria = df.iloc[:] 4 nigeria.head()
第一届世界杯于 1930 年举行。我们为年份创建一列,并选择所有 1930 年之后举行的比赛:
1 #creating a column for year and the first world cup was held in 1930 2 year = [] 3 for row in nigeria['date']: 4 year.append(int(row[:4])) 5 nigeria ['match_year']= year 6 nigeria_1930 = nigeria[nigeria.match_year >= 1930] 7 nigeria_1930.count()
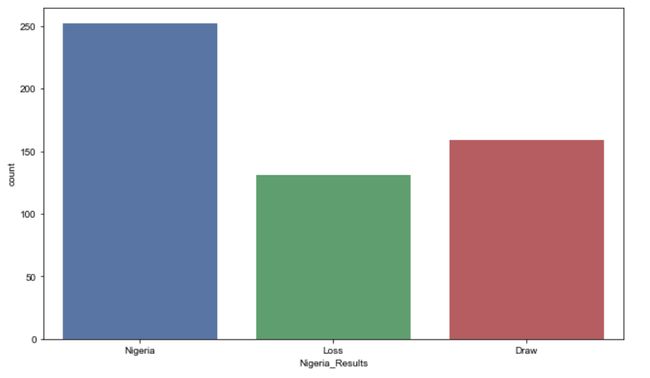
现在我们可以用图形表示这些年来尼日利亚队最普遍的比赛结果:
#what is the common game outcome for nigeria visualisation wins = [] for row in nigeria_1930['winning_team']: if row != 'Nigeria' and row != 'Draw': wins.append('Loss') else: wins.append(row) winsdf= pd.DataFrame(wins, columns=[ 'Nigeria_Results']) #plotting fig, ax = plt.subplots(1) fig.set_size_inches(10.7, 6.27) sns.set(style='darkgrid') sns.countplot(x='Nigeria_Results', data=winsdf)
每个参加世界杯的国家的胜率是非常有帮助性的指标,我们可以用它来预测此次比赛最可能的结果。
- 2.4 锁定参加世界杯的队伍:
我们为2018世界杯所有参赛队伍创建一个数据框,然后从该数据框中进一步筛选出从 1930 年起参加世界杯的队伍,并去掉重复的队伍:
1 #narrowing to team patcipating in the world cup 2 worldcup_teams = ['Australia', ' Iran', 'Japan', 'Korea Republic', 3 'Saudi Arabia', 'Egypt', 'Morocco', 'Nigeria', 4 'Senegal', 'Tunisia', 'Costa Rica', 'Mexico', 5 'Panama', 'Argentina', 'Brazil', 'Colombia', 6 'Peru', 'Uruguay', 'Belgium', 'Croatia', 7 'Denmark', 'England', 'France', 'Germany', 8 'Iceland', 'Poland', 'Portugal', 'Russia', 9 'Serbia', 'Spain', 'Sweden', 'Switzerland'] 10 df_teams_home = results[results['home_team'].isin(worldcup_teams)] 11 df_teams_away = results[results['away_team'].isin(worldcup_teams)] 12 df_teams = pd.concat((df_teams_home, df_teams_away)) 13 df_teams.drop_duplicates() 14 df_teams.count()
为年份创建一列,去掉 1930 年之前的比赛,并去掉不会影响到比赛结果的数据列,比如 date(日期)、home_score(主场得分)、away_score(客场得分)、tournament(锦标赛)、city(城市)、country(国家)、goal_difference(目标差异)和 match_year(比赛年份):
#create an year column to drop games before 1930 year = [] for row in df_teams['date']: year.append(int(row[:4])) df_teams['match_year'] = year df_teams_1930 = df_teams[df_teams.match_year >= 1930] df_teams_1930.head() #dropping columns that wll not affect matchoutcomes df_teams_1930 = df_teams.drop(['date', 'home_score', 'away_score', 'tournament', 'city', 'country', 'goal_difference', 'match_year'], axis=1) df_teams_1930.head()
为了简化模型的处理,我们修改一下预测标签。
如果主场队伍获胜,那么 winning_team(获胜队伍)一列显示“2”,如果平局则显示“1”,如果是客场队伍获胜则显示“0”:
1 #Building the model 2 #the prediction label: The winning_team column will show "2" if the home team has won, "1" if it was a tie, and "0" if the away team has won. 3 4 df_teams_1930 = df_teams_1930.reset_index(drop=True) 5 df_teams_1930.loc[df_teams_1930.winning_team == df_teams_1930.home_team,'winning_team']=2 6 df_teams_1930.loc[df_teams_1930.winning_team == 'Draw', 'winning_team']=1 7 df_teams_1930.loc[df_teams_1930.winning_team == df_teams_1930.away_team, 'winning_team']=0 8 9 df_teams_1930.head()
通过设置哑变量(dummy variables),我们将 home_team(主场队伍)和away _team(客场队伍)从分类变量转换成连续的输入。
这时可以使用 pandas 的 get_dummies() 函数,它会将分类列替换成一位有效值(one-hot,由数字‘1’和‘0’组成),以便将它们加载到 Scikit-learn 模型中。
接下来,我们将数据按照 70% 的训练数据集和 30% 的测试数据集分成 X 集和 Y 集:
1 #convert home team and away team from categorical variables to continous inputs 2 # Get dummy variables 3 final = pd.get_dummies(df_teams_1930, prefix=['home_team', 'away_team'], columns=['home_team', 'away_team']) 4 5 # Separate X and y sets 6 X = final.drop(['winning_team'], axis=1) 7 y = final["winning_team"] 8 y = y.astype('int') 9 10 # Separate train and test sets 11 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=42)
这里我们将使用分类算法:逻辑回归。这个算法的工作原理是什么?该算法利用逻辑函数来预测概率,从而可以测量出分类因变量与一个或多个自变量之间的关系。具体来说就是累积的逻辑分布。
换句话说,逻辑回归可以针对一组可以影响到结果的既定数据集(统计值)尝试预测结果(赢或输)。
在实践中这种方法的工作原理是:使用上述的两套“数据集”和比赛的实际结果,一次输入一场比赛到算法中。然后模型就会学习输入的每条数据对比赛结果产生了积极的效果还是消极的效果,以及影响的程度。
经过充分的(好)数据的训练后,就可以得到能够预测未来结果的模型,而模型的好坏程度取决于输入的数据。
之后我们将这些数据传递到算法中:
logreg = LogisticRegression() logreg.fit(X_train, y_train) score = logreg.score(X_train, y_train) score2 = logreg.score(X_test, y_test) print("Training set accuracy: ", '%.3f'%(score)) print("Test set accuracy: ", '%.3f'%(score2))
Training set accuracy: 0.573 Test set accuracy: 0.551
我们的模型子训练数据集的正确率为 57%,在测试数据集上的正确率为 55%。虽然结果不是很好,但是我们先继续下一步。
接下来我们建立需要配置到模型的数据框。
首先我们加载 2018 年 4 月 FIFA 排名数据和小组赛分组状况的数据集。由于世界杯比赛中没有“主场”和“客场”,所以我们把 FIFA 排名靠前的队伍作为“喜爱”的比赛队伍,将他们放到“home_teams”(主场队伍)一列。然后我们根据每个队伍的排名将他们加入到新的预测数据集中。下一步是创建默认变量,并部署机器学习模型。
2018 年 4 月 FIFA 排名数据:https://us.soccerway.com/teams/rankings/fifa/?ICID=TN_03_05_01
小组赛分组状况的数据集:https://fixturedownload.com/results/fifa-world-cup-2018
#adding Fifa rankings #the team which is positioned higher on the FIFA Ranking will be considered "favourite" for the match #and therefore, will be positioned under the "home_teams" column #since there are no "home" or "away" teams in World Cup games. # Loading new datasets ranking = pd.read_csv('C:/Coding/FIFA2018-World-cup/datasets/fifa_rankings.csv') fixtures = pd.read_csv('C:/Coding/FIFA2018-World-cup/datasets/fixtures.csv') # List for storing the group stage games pred_set = [] # Create new columns with ranking position of each team fixtures.insert(1, 'first_position', fixtures['Home Team'].map(ranking.set_index('Team')['Position'])) fixtures.insert(2, 'second_position', fixtures['Away Team'].map(ranking.set_index('Team')['Position'])) # We only need the group stage games, so we have to slice the dataset fixtures = fixtures.iloc[:48, :] # Loop to add teams to new prediction dataset based on the ranking position of each team for index, row in fixtures.iterrows(): if row['first_position'] < row['second_position']: pred_set.append({'home_team': row['Home Team'], 'away_team': row['Away Team'], 'winning_team': None}) else: pred_set.append({'home_team': row['Away Team'], 'away_team': row['Home Team'], 'winning_team': None}) pred_set = pd.DataFrame(pred_set) backup_pred_set = pred_set # Get dummy variables and drop winning_team column pred_set = pd.get_dummies(pred_set, prefix=['home_team', 'away_team'], columns=['home_team', 'away_team']) # Add missing columns compared to the model's training dataset missing_cols = set(final.columns) - set(pred_set.columns) for c in missing_cols: pred_set[c] = 0 pred_set = pred_set[final.columns] # Remove winning team column pred_set = pred_set.drop(['winning_team'], axis=1) pred_set.head()
- 2.5 比赛结果预测:
首先,我们将模型部署到小组赛中:
#group matches predictions = logreg.predict(pred_set) for i in range(fixtures.shape[0]): print(backup_pred_set.iloc[i, 1] + " and " + backup_pred_set.iloc[i, 0]) if predictions[i] == 2: print("Winner: " + backup_pred_set.iloc[i, 1]) elif predictions[i] == 1: print("Draw") elif predictions[i] == 0: print("Winner: " + backup_pred_set.iloc[i, 0]) print('Probability of ' + backup_pred_set.iloc[i, 1] + ' winning: ', '%.3f'%(logreg.predict_proba(pred_set)[i][2])) print('Probability of Draw: ', '%.3f'%(logreg.predict_proba(pred_set)[i][1])) print('Probability of ' + backup_pred_set.iloc[i, 0] + ' winning: ', '%.3f'%(logreg.predict_proba(pred_set)[i][0])) print("")
Russia and Saudi Arabia Winner: Russia Probability of Russia winning: 0.667 Probability of Draw: 0.223 Probability of Saudi Arabia winning: 0.111 Uruguay and Egypt Winner: Uruguay Probability of Uruguay winning: 0.583 Probability of Draw: 0.352 Probability of Egypt winning: 0.065 Iran and Morocco Draw Probability of Iran winning: 0.217 Probability of Draw: 0.407 Probability of Morocco winning: 0.376 Portugal and Spain Winner: Spain Probability of Portugal winning: 0.302 Probability of Draw: 0.344 Probability of Spain winning: 0.354 France and Australia Winner: France Probability of France winning: 0.628 Probability of Draw: 0.227 Probability of Australia winning: 0.145 Argentina and Iceland Winner: Argentina Probability of Argentina winning: 0.803 Probability of Draw: 0.161 Probability of Iceland winning: 0.036 Peru and Denmark Winner: Peru Probability of Peru winning: 0.439 Probability of Draw: 0.171 Probability of Denmark winning: 0.391 Croatia and Nigeria Winner: Croatia Probability of Croatia winning: 0.590 Probability of Draw: 0.258 Probability of Nigeria winning: 0.152 Costa Rica and Serbia Winner: Serbia Probability of Costa Rica winning: 0.315 Probability of Draw: 0.324 Probability of Serbia winning: 0.361 Germany and Mexico Winner: Germany Probability of Germany winning: 0.567 Probability of Draw: 0.282 Probability of Mexico winning: 0.150 Brazil and Switzerland Winner: Brazil Probability of Brazil winning: 0.775 Probability of Draw: 0.138 Probability of Switzerland winning: 0.087 Sweden and Korea Republic Winner: Sweden Probability of Sweden winning: 0.503 Probability of Draw: 0.329 Probability of Korea Republic winning: 0.168 Belgium and Panama Winner: Belgium Probability of Belgium winning: 0.765 Probability of Draw: 0.145 Probability of Panama winning: 0.090 England and Tunisia Winner: England Probability of England winning: 0.649 Probability of Draw: 0.292 Probability of Tunisia winning: 0.059 Colombia and Japan Winner: Colombia Probability of Colombia winning: 0.511 Probability of Draw: 0.210 Probability of Japan winning: 0.280 Poland and Senegal Winner: Poland Probability of Poland winning: 0.612 Probability of Draw: 0.223 Probability of Senegal winning: 0.165 Egypt and Russia Winner: Russia Probability of Egypt winning: 0.225 Probability of Draw: 0.297 Probability of Russia winning: 0.478 Portugal and Morocco Winner: Portugal Probability of Portugal winning: 0.486 Probability of Draw: 0.377 Probability of Morocco winning: 0.138 Uruguay and Saudi Arabia Winner: Uruguay Probability of Uruguay winning: 0.668 Probability of Draw: 0.259 Probability of Saudi Arabia winning: 0.073 Spain and Iran Winner: Spain Probability of Spain winning: 0.695 Probability of Draw: 0.247 Probability of Iran winning: 0.058 Denmark and Australia Winner: Denmark Probability of Denmark winning: 0.551 Probability of Draw: 0.241 Probability of Australia winning: 0.207 France and Peru Winner: France Probability of France winning: 0.635 Probability of Draw: 0.215 Probability of Peru winning: 0.150 Argentina and Croatia Winner: Argentina Probability of Argentina winning: 0.599 Probability of Draw: 0.255 Probability of Croatia winning: 0.146 Brazil and Costa Rica Winner: Brazil Probability of Brazil winning: 0.800 Probability of Draw: 0.147 Probability of Costa Rica winning: 0.053 Iceland and Nigeria Winner: Nigeria Probability of Iceland winning: 0.278 Probability of Draw: 0.248 Probability of Nigeria winning: 0.474 Switzerland and Serbia Winner: Switzerland Probability of Switzerland winning: 0.402 Probability of Draw: 0.228 Probability of Serbia winning: 0.370 Belgium and Tunisia Winner: Belgium Probability of Belgium winning: 0.619 Probability of Draw: 0.253 Probability of Tunisia winning: 0.128 Mexico and Korea Republic Winner: Mexico Probability of Mexico winning: 0.504 Probability of Draw: 0.327 Probability of Korea Republic winning: 0.169 Germany and Sweden Winner: Germany Probability of Germany winning: 0.571 Probability of Draw: 0.228 Probability of Sweden winning: 0.201 England and Panama Winner: England Probability of England winning: 0.781 Probability of Draw: 0.178 Probability of Panama winning: 0.041 Senegal and Japan Winner: Senegal Probability of Senegal winning: 0.397 Probability of Draw: 0.278 Probability of Japan winning: 0.325 Poland and Colombia Draw Probability of Poland winning: 0.379 Probability of Draw: 0.391 Probability of Colombia winning: 0.230 Uruguay and Russia Winner: Uruguay Probability of Uruguay winning: 0.403 Probability of Draw: 0.388 Probability of Russia winning: 0.209 Egypt and Saudi Arabia Winner: Egypt Probability of Egypt winning: 0.544 Probability of Draw: 0.216 Probability of Saudi Arabia winning: 0.240 Portugal and Iran Winner: Portugal Probability of Portugal winning: 0.548 Probability of Draw: 0.353 Probability of Iran winning: 0.099 Spain and Morocco Winner: Spain Probability of Spain winning: 0.650 Probability of Draw: 0.267 Probability of Morocco winning: 0.083 France and Denmark Winner: France Probability of France winning: 0.621 Probability of Draw: 0.159 Probability of Denmark winning: 0.220 Peru and Australia Winner: Peru Probability of Peru winning: 0.463 Probability of Draw: 0.250 Probability of Australia winning: 0.288 Argentina and Nigeria Winner: Argentina Probability of Argentina winning: 0.708 Probability of Draw: 0.222 Probability of Nigeria winning: 0.070 Croatia and Iceland Winner: Croatia Probability of Croatia winning: 0.734 Probability of Draw: 0.185 Probability of Iceland winning: 0.080 Mexico and Sweden Winner: Mexico Probability of Mexico winning: 0.465 Probability of Draw: 0.264 Probability of Sweden winning: 0.271 Germany and Korea Republic Winner: Germany Probability of Germany winning: 0.598 Probability of Draw: 0.282 Probability of Korea Republic winning: 0.120 Brazil and Serbia Winner: Brazil Probability of Brazil winning: 0.714 Probability of Draw: 0.165 Probability of Serbia winning: 0.120 Switzerland and Costa Rica Winner: Switzerland Probability of Switzerland winning: 0.587 Probability of Draw: 0.213 Probability of Costa Rica winning: 0.200 Poland and Japan Winner: Poland Probability of Poland winning: 0.551 Probability of Draw: 0.242 Probability of Japan winning: 0.206 Colombia and Senegal Winner: Colombia Probability of Colombia winning: 0.577 Probability of Draw: 0.194 Probability of Senegal winning: 0.229 Tunisia and Panama Winner: Tunisia Probability of Tunisia winning: 0.631 Probability of Draw: 0.257 Probability of Panama winning: 0.113 Belgium and England Winner: England Probability of Belgium winning: 0.273 Probability of Draw: 0.235 Probability of England winning: 0.492
之后进行16强的模拟:
# List of tuples before group_16 = [('Uruguay', 'Portugal'), ('France', 'Croatia'), ('Brazil', 'Mexico'), ('England', 'Colombia'), ('Spain', 'Russia'), ('Argentina', 'Peru'), ('Germany', 'Switzerland'), ('Poland', 'Belgium')]
def clean_and_predict(matches, ranking, final, logreg):
# Initialization of auxiliary list for data cleaning
positions = []
# Loop to retrieve each team's position according to FIFA ranking
for match in matches:
positions.append(ranking.loc[ranking['Team'] == match[0],'Position'].iloc[0])
positions.append(ranking.loc[ranking['Team'] == match[1],'Position'].iloc[0])
# Creating the DataFrame for prediction
pred_set = []
# Initializing iterators for while loop
i = 0
j = 0
# 'i' will be the iterator for the 'positions' list, and 'j' for the list of matches (list of tuples)
while i < len(positions):
dict1 = {}
# If position of first team is better, he will be the 'home' team, and vice-versa
if positions[i] < positions[i + 1]:
dict1.update({'home_team': matches[j][0], 'away_team': matches[j][1]})
else:
dict1.update({'home_team': matches[j][1], 'away_team': matches[j][0]})
# Append updated dictionary to the list, that will later be converted into a DataFrame
pred_set.append(dict1)
i += 2
j += 1
# Convert list into DataFrame
pred_set = pd.DataFrame(pred_set)
backup_pred_set = pred_set
# Get dummy variables and drop winning_team column
pred_set = pd.get_dummies(pred_set, prefix=['home_team', 'away_team'], columns=['home_team', 'away_team'])
# Add missing columns compared to the model's training dataset
missing_cols2 = set(final.columns) - set(pred_set.columns)
for c in missing_cols2:
pred_set[c] = 0
pred_set = pred_set[final.columns]
# Remove winning team column
pred_set = pred_set.drop(['winning_team'], axis=1)
# Predict!
predictions = logreg.predict(pred_set)
for i in range(len(pred_set)):
print(backup_pred_set.iloc[i, 1] + " and " + backup_pred_set.iloc[i, 0])
if predictions[i] == 2:
print("Winner: " + backup_pred_set.iloc[i, 1])
elif predictions[i] == 1:
print("Draw")
elif predictions[i] == 0:
print("Winner: " + backup_pred_set.iloc[i, 0])
print('Probability of ' + backup_pred_set.iloc[i, 1] + ' winning: ' , '%.3f'%(logreg.predict_proba(pred_set)[i][2]))
print('Probability of Draw: ', '%.3f'%(logreg.predict_proba(pred_set)[i][1]))
print('Probability of ' + backup_pred_set.iloc[i, 0] + ' winning: ', '%.3f'%(logreg.predict_proba(pred_set)[i][0]))
print("")
clean_and_predict(group_16, ranking, final, logreg)
Portugal and Uruguay Winner: Portugal Probability of Portugal winning: 0.428 Probability of Draw: 0.285 Probability of Uruguay winning: 0.287 France and Croatia Winner: France Probability of France winning: 0.481 Probability of Draw: 0.252 Probability of Croatia winning: 0.267 Brazil and Mexico Winner: Brazil Probability of Brazil winning: 0.695 Probability of Draw: 0.209 Probability of Mexico winning: 0.096 England and Colombia Winner: England Probability of England winning: 0.516 Probability of Draw: 0.368 Probability of Colombia winning: 0.116 Spain and Russia Winner: Spain Probability of Spain winning: 0.529 Probability of Draw: 0.280 Probability of Russia winning: 0.191 Argentina and Peru Winner: Argentina Probability of Argentina winning: 0.713 Probability of Draw: 0.212 Probability of Peru winning: 0.075 Germany and Switzerland Winner: Germany Probability of Germany winning: 0.672 Probability of Draw: 0.192 Probability of Switzerland winning: 0.137 Belgium and Poland Winner: Belgium Probability of Belgium winning: 0.513 Probability of Draw: 0.202 Probability of Poland winning: 0.285
之后依次进行四分之一、半决赛、决赛的模拟:
四分之一:
# List of matches quarters = [('Portugal', 'France'), ('Spain', 'Argentina'), ('Brazil', 'England'), ('Germany', 'Belgium')] clean_and_predict(quarters, ranking, final, logreg)
Portugal and France Winner: Portugal Probability of Portugal winning: 0.437 Probability of Draw: 0.256 Probability of France winning: 0.307 Argentina and Spain Winner: Argentina Probability of Argentina winning: 0.518 Probability of Draw: 0.262 Probability of Spain winning: 0.220 Brazil and England Winner: Brazil Probability of Brazil winning: 0.525 Probability of Draw: 0.216 Probability of England winning: 0.260 Germany and Belgium Winner: Germany Probability of Germany winning: 0.563 Probability of Draw: 0.269 Probability of Belgium winning: 0.167
半决赛:
# List of matches semi = [('Portugal', 'Brazil'), ('Argentina', 'Germany')] clean_and_predict(semi, ranking, final, logreg)
Brazil and Portugal Winner: Brazil Probability of Brazil winning: 0.705 Probability of Draw: 0.152 Probability of Portugal winning: 0.143 Germany and Argentina Winner: Germany Probability of Germany winning: 0.441 Probability of Draw: 0.264 Probability of Argentina winning: 0.295
决赛:
# Finals finals = [('Brazil', 'Germany')] clean_and_predict(finals, ranking, final, logreg)
Germany and Brazil Winner: Brazil Probability of Germany winning: 0.359 Probability of Draw: 0.220 Probability of Brazil winning: 0.421
- 3. 写在最后:
根据该模型,巴西将有可能获得本届世界杯的冠军。
进一步的研究和提高领域:
- 为提高数据集的质量,可以利用 FIFA 的比赛数据评估每个球员的水平;
- 混淆矩阵可以帮助我们分析模型预测的哪场有误;
- 我们可以尝试将多个模型组合在一起,提高预测准确度。