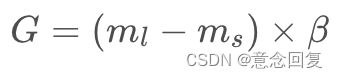不均衡样本集的重采样

目录

1 背景

2 为什么很多分类模型在训练数据不均衡时会出现问题？

3 处理样本不均衡问题——基于数据的方法

3.1 随机采样

3.2 SMOTE

3.2.1 概念

3.2.2 伪代码

3.2.3 python程序

3.3 Borderline SMOTE

3.3.1 概念

3.3.2 python实现

3.4 ADASYN自适应综合过采样

3.5 Informed Undersampling

3.5.1 Easy Ensemble算法

3.5.2 Balance Cascade算法

4 处理样本不均衡问题——基于算法的方法

---

1 背景

        在训练二分类模型时， 例如医疗诊断、 网络入侵检测、 信用卡反诈骗等， 经常会遇到正负样本不均衡的问题。 对于很多分类算法， 如果直接采用不均衡的样本集来进行训练学习， 会存在一些问题。 例如， 如果正负样本比例达到1∶ 99， 则分类器简单地将所有样本都判为负样本就能达到99%的正确率， 显然这并不是我们想要的， 我们想让分类器在正样本和负样本上都有足够的准确率和召回率。

2 为什么很多分类模型在训练数据不均衡时会出现问题？

本质原因是模型在训练时优化的目标函数和人们在测试时使用的评价标准不一致。

1. 这种“不一致”可能是由于训练数据的样本分布与测试时期望的样本分布不一致， 例如， 在训练时优化的是整个训练集（正负样本比例可能是1∶ 99） 的正确率， 而测试时可能想要模型在正样本和负样本上的平均正确率尽可能大（实际上是期望正负样本比例为1∶ 1） ；
2. 也可能是由于训练阶段不同类别的权重（重要性） 与测试阶段不一致，例如训练时认为所有样本的贡献是相等的， 而测试时假阳性样本（False Positive）和伪阴性样本（False Negative） 有着不同的代价。

3 处理样本不均衡问题——基于数据的方法

       对数据进行重采样， 使原本不均衡的样本变得均衡。 首先， 记样本数大的类别为Cmaj， 样本数小的类别为Cmin， 它们对应的样本集分别为Smaj和Smin。 根据题设， 有|Smaj|>>|Smin。

3.1 随机采样

         最简单的处理不均衡样本集的方法是随机采样。 采样一般分为：过采样（Oversampling） 和欠采样（Under-sampling） 。

• 随机过采样是从少数类样本集Smin中随机重复抽取样本（有放回） 以得到更多样本；
• 随机欠采样则相反， 从多数类样本集Smaj中随机选取较少的样本（有放回或无放回） 。

        直接的随机采样虽然可以使样本集变得均衡， 但会带来一些问题， 比如，

• 过采样对少数类样本进行了多次复制， 扩大了数据规模， 增加了模型训练的复杂度， 同时也容易造成过拟合；
• 欠采样会丢弃一些样本， 可能会损失部分有用信息， 造成模型只学到了整体模式的一部分。

3.2 SMOTE

3.2.1 概念

论文地址：https://arxiv.org/pdf/1106.1813.pdf

        为了解决上述问题， 通常在过采样时并不是简单地复制样本， 而是采用一些方法生成新的样本。 例如， SMOTE算法：

1. 对少数类样本集Smin中每个样本x， 从它在Smin中的K近邻中随机选一个样本y；
2. 然后在x,y连线上随机选取一点作为新合成的样本（根据需要的过采样倍率重复上述过程若干次）

        如下图所示。 这种合成新样本的过采样方法可以降低过拟合的风险：

        SMOTE算法为每个少数类样本合成相同数量的新样本， 这可能会增大类间重叠度， 并且会生成一些不能提供有益信息的样本。 也就是：该算法无法克服非平衡数据集的数据分布问题,容易产生分布边缘化问题。由于负类样本的分布决定了其可选择的近邻，如果一个负类样本处在负类样本集的分布边缘，则由此负类样本和相邻样本产生的“人造”样本也会处在这个边缘，且会越来越边缘化，从而模糊了正类样本和负类样本的边界，而且使边界变得越来越模糊。这种边界模糊性，虽然使数据集的平衡性得到了改善，但加大了分类算法进行分类的难度。

3.2.2 伪代码

 

3.2.3 python程序

# pip install imbalanced-learn

from collections import Counter
from sklearn.datasets import make_classification
from imblearn.over_sampling import SMOTE
import matplotlib.pyplot as plt


X, y = make_classification(n_classes=2, class_sep=2,
                           weights=[0.1, 0.9], n_informative=2, n_redundant=0, flip_y=0,
                           n_features=2, n_clusters_per_class=1, n_samples=100,random_state=10)
print('Original dataset shape %s' % Counter(y))
x1 = X[y==1]
x2 = X[y==0]
plt.scatter(x1[:, 0], x1[:, 1])
plt.scatter(x2[:, 0], x2[:, 1])
plt.show()

sm = SMOTE(random_state=42)
X_res, y_res = sm.fit_resample(X, y)
print('Resampled dataset shape %s' % Counter(y_res))
x1 = X_res[y_res==1]
x2 = X_res[y_res==0]
plt.scatter(x1[:, 0], x1[:, 1])
plt.scatter(x2[:, 0], x2[:, 1])
plt.show()

3.3 Borderline SMOTE

3.3.1 概念

        论文地址：https://sci2s.ugr.es/keel/keel-dataset/pdfs/2005-Han-LNCS.pdf

        Borderline SMOTE是在SMOTE基础上改进的过采样算法，该算法仅使用边界上的少数类样本来合成新样本，从而改善样本的类别分布。
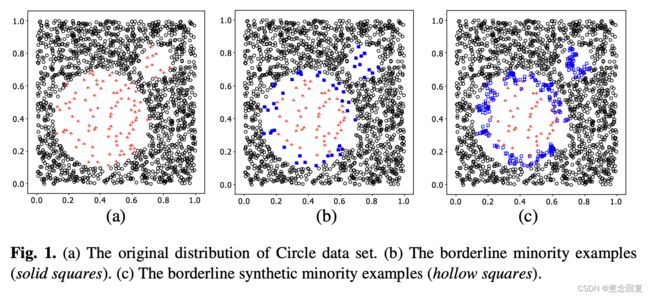
  Borderline SMOTE采样过程是将少数类样本分为3类，分别为Safe、Danger和Noise，具体说明如下。最后，仅对表为Danger的少数类样本过采样。

• Safe，样本周围一半以上均为少数类样本，如图中点A  
• Danger：样本周围一半以上均为多数类样本，视为在边界上的样本，如图中点B
• Noise：样本周围均为多数类样本，视为噪音，如图中点C

• 图a 是原始数据
• 图b是识别出的边界上的少量样本
• 图c是使用 Borderline SMOTE生成假样本

        Borderline-SMOTE又可分为Borderline-SMOTE1和Borderline-SMOTE2：

• Borderline-SMOTE1在对Danger点生成新样本时，在K近邻随机选择少数类样本（与SMOTE相同）；
• Borderline-SMOTE2则是在k近邻中的任意一个样本(不关注样本类别)，但是生成的样本更靠近少数类样本。

3.3.2 python实现

from collections import Counter
from sklearn.datasets import make_classification
from imblearn.over_sampling import SMOTE, BorderlineSMOTE
import matplotlib.pyplot as plt


def borderline_smote(X, y):
    # X, y = make_classification(n_classes=2, class_sep=2,
    #                            weights=[0.1, 0.9], n_informative=2, n_redundant=0, flip_y=0,
    #                            n_features=2, n_clusters_per_class=1, n_samples=100, random_state=9)
    sm = BorderlineSMOTE(random_state=42, kind="borderline-1")
    X_res, y_res = sm.fit_resample(X, y)
    print('Resampled dataset shape %s' % Counter(y_res))
    x1 = X_res[y_res==1]
    x2 = X_res[y_res==0]
    plt.scatter(x1[:, 0], x1[:, 1])
    plt.scatter(x2[:, 0], x2[:, 1])
    plt.show()


if __name__ == "__main__":
    X, y = make_classification(n_classes=2, class_sep=2,
                               weights=[0.1, 0.9], n_informative=2, n_redundant=0, flip_y=0,
                               n_features=2, n_clusters_per_class=1, n_samples=100)
    print('Original dataset shape %s' % Counter(y))
    x1 = X[y == 1]
    x2 = X[y == 0]
    plt.scatter(x1[:, 0], x1[:, 1])
    plt.scatter(x2[:, 0], x2[:, 1])
    plt.show()
    borderline_smote(X, y)

3.4 ADASYN自适应综合过采样

       论文地址：​​​​​​​https://sci2s.ugr.es/keel/pdf/algorithm/congreso/2008-He-ieee.pdfhttps://sci2s.ugr.es/keel/pdf/algorithm/congreso/2008-He-ieee.pdf

        ADASYN （adaptive synthetic sampling）自适应合成抽样，与Borderline SMOTE相似，对不同的少数类样本赋予不同的权重，从而生成不同数量的样本。

       具体流程如下：

步骤1：计算需要合成的样本数量，公式如下： 
    

       其中，ml为多数类样本数量，ms为少数类样本数量，β∈[0,1]随机数，若β等于1，采样后正负比例为1:1。

步骤2：计算K近邻中多数类占比，公式如下：

        

      其中，∆i为K近邻中多数类样本数，i = 1,2,3,……,ms 

步骤3：对ri标准化，公式如下：

         

 步骤4：根据样本权重，计算每个少数类样本需生成新样本的数目，公式如下：

          

步骤5：根据g计算每个少数样本需生成的数目，根据SMOTE算法生成样本，公式如下： 

          

     其中，si为合成样本，xi是少数类样本中第i个样本，xzi是xi的K近邻中随机选取的一个少数类样本， λ∈[0,1]的随机数。 

3.5 Informed Undersampling

       对于欠采样， 可以采用Informed Undersampling来解决由于随机欠采样带来的数据丢失问题。 常见的Informed Undersampling算法有：

3.5.1 Easy Ensemble算法

       每次从多数类Smaj中上随机抽取一个子集E(|E|≈|Smin|)， 然后用E+Smin训练一个分类器； 重复上述过程若干次， 得到多个分类器，最终的分类结果是这多个分类器结果的融合 .

3.5.2 Balance Cascade算法

       级联结构， 在每一级中从多数类Smaj中随机抽取子集E， 用E+Smin训练该级的分类器； 然后将Smaj中能够被当前分类器正确判别的样本剔除掉， 继续下一级的操作， 重复若干次得到级联结构； 最终的输出结果也是各级分类器结果的融合。

       其他诸如NearMiss（ 利用K近邻信息挑选具有代表性的样本） 、 Onesided Selection（ 采用数据清理技术） 等算法。

       在实际应用中， 具体的采样操作可能并不总是如上述几个算法一样， 但基本思路很多时候还是一致的。 例如， 基于聚类的采样方法， 利用数据的类簇信息来指导过采样/欠采样操作； 经常用到的数据扩充方法也是一种过采样， 对少数类样本进行一些噪声扰动或变换（ 如图像数据集中对图片进行裁剪、 翻转、 旋转、 加光照等） 以构造出新的样本； 而Hard Negative Mining则是一种欠采样， 把比较难的样本抽出来用于迭代分类器。

4 处理样本不均衡问题——基于算法的方法

• 在样本不均衡时， 也可以通过改变模型训练时的目标函数（ 如代价敏感学习中不同类别有不同的权重） 来矫正这种不平衡性；
• 当样本数目极其不均衡时， 也可以将问题转化为单类学习（ one-class learning） 、 异常检测（ anomaly detection） 。 

不平衡数据处理之SMOTE、Borderline SMOTE和ADASYN详解及Python使用_猫新人的博客-CSDN博客_borderline smote