【数据分析与挖掘】财政收入影响因素分析及预测模型(有数据集和代码)

案例背景

• 在我国现行的分税制财政管理体制下，地方财政收人不仅是国家财政收入的重要组成部分，而且具有其相对独立的构成内容。如何有效的利用地方财政收入，合理的分配，来促进地方的发展，提高市民的收入和生活质量是每个地方政府需要考虑的首要问题。因此，对地方财政收人进行预测，不仅是必要的，而且也是可能的。科学、合理地预测地方财政收人，对于克服年度地方预算收支规模确定的随意性和盲目性，正确处理地方财政与经济的相互关系具有十分重要的意义。
• 某市作为改革开放的前沿城市，其经济发展在全国经济中的地位举足轻重。目前，该市在财政收入规模、结构等方面与北京、上海、深圳等城市仍有一定差距，存在不断完善的空间。本案例旨在通过研究，发现影响该市目前以及未来地方财源建设的因素，并对其进行深入分析，提出对该市地方财源优化的具体建议，供政府决策参考，同时为其他经济发展较快的城市提供借鉴。

原始数据情况

考虑到数据的可得性，本案例所用的财政收入分为地方一般预算收入和政府性基金收入。地方一般预算收入包括：(1)税收收入，主要包括企业所得税和地方所得税中中央和地方共享的40%，地方享有的 25%的增值税、营业税、印花税等；(2)非税收入，包括专项收入、行政事业性收费、罚没收入、国有资本经营收入和其他收入等。政府性基金收入是国家通过向社会征收以及出让土地、发行彩票等方式取得收入，并专项用于支持特定基础设施建设和社会事业发展的收入。

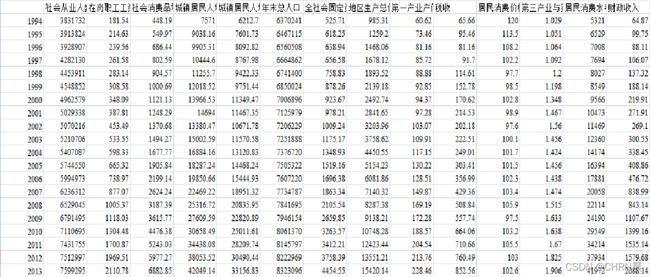
由于1994年我国对财政体制进行了重大改革，开始实行分税制财政体制，影响了财政收入相关数据的连续性，在1994年前后不具有可比性。由于没有合适的数学手段来调整这种数据的跃变，仅对1994年及其以后的数据进行分析，本案例所用数据均来自《某市统计年鉴》(1995-2014)。

某市1994-2013年财政收入以及相关因素的数据

挖掘目标

1. 梳理影响地方财政收入的关键特征，分析、识别影响地方财政收入的关键特征的选择模型；
2. 结合目标1的因素分析，对某市2015年的财政总收入及各个类别收入进行预测。

初步分析

• 在以往的文献中，对影响财政收入的因素的分析中大多使用普通最小二乘法来对回归模型的系数进行估计，预测变量的选取则采用的是逐步回归。然而，无论是最小二乘法还是逐步回归，都有其不足之处。它们一般都局限于局部最优解而不是全局最优解。
• Lasso是近年来被广泛应用于参数估计和变量选择的方法之一，并且Lasso进行变量选择在确定的条件下已经被证明是一致的。案例选用了Adaptive-Lasso方法来探究地方财政收入与各因素之间的关系。

总体流程

 1)	从某市统计局网站以及各统计年鉴搜集到该市财政收入以及各类别收入相关数据；
 
 2)	利用1）形成的已完成数据预处理的建模数据，建立Adaptive-Lasso变量选择模型；
 
 3)	在2）的基础上建立单变量的灰色预测模型以及人工神经网络预测模型；
 
 4)	利用3）的预测值代入构建好的人工神经网络模型中，从而得到2014/2015年某市财政收入以及各类别收入的预测值。

数据探索分析

影响财政收入(y)的因素有很多，通过经济理论对财政收入的解释以及对实践的观察，考虑一些与能源消耗关系密切并且直观上有线性关系的因素，选取以下因素为自变量，分析它们之间的关系。

• 社会从业人数(x1)：就业人数的上升伴随着居民消费水平的提高，从而间接影响财政收入的增加。
• 在岗职工工资总额(x2)：反映的是社会分配情况，主要影响财政收入中的个人所得税、房产税以及潜在消费能力。
• 社会消费品零售总额(x3)：代表社会整体消费情况，是可支配收入在经济生活中的实现。当社会消费品零售总额增长时，表明社会消费意愿强烈，部分程度上会导致财政收入中增值税的增长；同时当消费增长时，也会引起经济系统中其他方面发生变动，最终导致财政收入的增长。
• 城镇居民人均可支配收入(x4)：居民收入越高消费能力越强，同时意味着其工作积极性越高，创造出的财富越多，从而能带来财政收入的更快和持续增长。
• 城镇居民人均消费性支出(x5)：居民在消费商品的过程中会产生各种税费，税费又是调节生产规模的手段之一。在商品经济发达的如今，居民消费的越多，对财政收入的贡献就越大。
• 年末总人口(x6)：在地方经济发展水平既定的条件下，人均地方财政收入与地方人口数呈反比例变化。
• 全社会固定资产投资额(x7)：是建造和购置固定资产的经济活动，即固定资产再生产活动。主要通过投资来促进经济增长，扩大税源，进而拉动财政税收收入整体增长。
• 地区生产总值(x8)：表示地方经济发展水平。一般来讲，政府财政收入来源于即期的地区生产总值。在国家经济政策不变、社会秩序稳定的情况下，地方经济发展水平与地方财政收入之间存在着密切的相关性，越是经济发达的地区，其财政收入的规模就越大。
• 第一产业产值(x9)：取消农业税、实施三农政策，第一产业对财政收入的影响更小。
• 税收(x10)：由于其具有征收的强制性、无偿性和固定性特点，可以为政府履行其职能提供充足的资金来源。因此，各国都将其作为政府财政收入的最重要的收入形式和来源。
• 居民消费价格指数(x11)：反映居民家庭购买的消费品及服务价格水平的变动情况，影响城乡居民的生活支出和国家的财政收入。
• 第三产业与第二产业产值比(x12)：表示产业结构。三次产业生产总值代表国民经济水平，是财政收入的主要影响因素，当产业结构逐步优化时，财政收入也会随之增加。
• 居民消费水平(x13)：在很大程度上受整体经济状况GDP的影响，从而间接影响地方财政收入。

描述分析

#-*- coding: utf-8 -*-
import numpy as np
import pandas as pd
inputfile = '../data/data1.csv' #输入的数据文件
data = pd.read_csv(inputfile) #读取数据
r = [data.min(), data.max(), data.mean(), data.std()] #依次计算最小值、最大值、均值、标准差
r = pd.DataFrame(r, index = ['Min', 'Max', 'Mean', 'STD']).T  #计算相关系数矩阵
np.round(r, 2) #保留两位小数

对已有数据进行描述性统计分析，获得对数据的整体性认识。

可见财政收入（y）的均值和标准差分别为618.08和609.25，这说明:第一，某市各年份财政收入存在较大差异。第二，2008年后，某市各年份财政收入大幅上升。

相关分析

相关系数可以用来描述定量变量之间的关系，初步判断因变量与解释变量之间是否具有线性相关性。

#-*- coding: utf-8 -*-
import numpy as np
import pandas as pd
inputfile = '../data/data1.csv' #输入的数据文件
data = pd.read_csv(inputfile) #读取数据
np.round(data.corr(method = 'pearson'), 2) #计算相关系数矩阵，保留两位小数

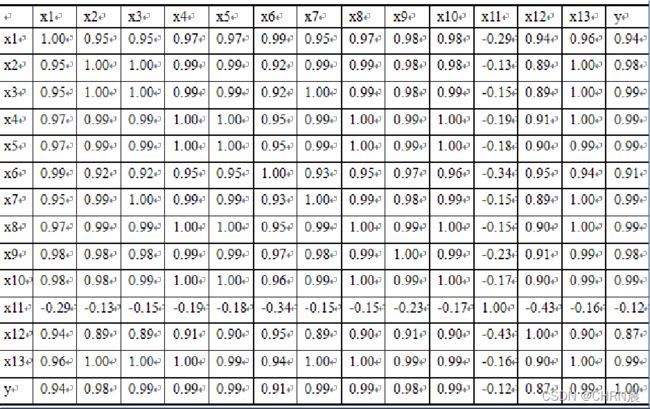
由相关矩阵可以看出居民消费价格指数(x11) 与财政收入的线性关系不显著，而且呈现负相关。其余变量均与财政收入呈现高度的正相关关系。

变量选择

运用LARS 算法来解决Adaptive-Lasso 估计，该算法会寻找一个最优解。用Python编制相应的程序后运行得到如下结果。

#-*- coding: utf-8 -*-
import pandas as pd
inputfile = '../data/data1.csv' #输入的数据文件
data = pd.read_csv(inputfile) #读取数据

#导入AdaptiveLasso算法，要在较新的Scikit-Learn才有。
from sklearn.linear_model import AdaptiveLasso
model = AdaptiveLasso(gamma=1)
model.fit(data.iloc[:,0:13],data['y'])
model.coef_ #各个特征的系数

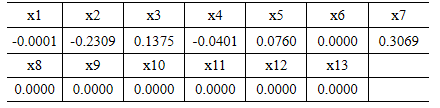
可看出，年末总人口、地区生产总值、第一产业产值、税收、居民消费价格指数、第三产业与第二产业产值比以及居民消费水平等因素的系数为0，即在模型建立的过程中这几个变量被剔除了。这是因为居民消费水平与城镇居民人均消费性支出存在明显的共线性，Adaptive-Lasso方法在构建模型的过程中剔除了这个变量；由于某市存在流动人口与外来打工人口多的特性，年末总人口并不显著影响某市财政收入；居民消费价格指数与财政收入的相关性太小以致可以忽略；由于农牧业各税在各项税收总额中所占比重过小，而且该市于2005年取消了农业税，因而第一产业对地方财政收入的贡献率极低；其他变量被剔除均有类似于上述的原因。

利用Adaptive-Lasso 方法识别影响财政收入的关键影响因素是社会从业人数、在岗职工工资总额、社会消费品零售总额、城镇居民人均可支配收入、城镇居民人均消费性支出以及全社会固定资产投资额。

财政收入及各类别收入预测模型:

某市财政收入预测模型

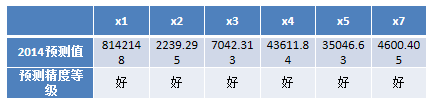
对Adaptive-Lasso 变量选择方法识别的影响财政收入的因素建立灰色预测与神经网络的组合预测模型, Python及流行的扩展库并没有提供灰色预测功能，因此自行编写灰色预测函数（GM11.py）。预测结果的精度等级见下表。

#-*- coding: utf-8 -*-

def GM11(x0): #自定义灰色预测函数
  import numpy as np
  x1 = x0.cumsum() #1-AGO序列
  z1 = (x1[:len(x1)-1] + x1[1:])/2.0 #紧邻均值（MEAN）生成序列
  z1 = z1.reshape((len(z1),1))
  B = np.append(-z1, np.ones_like(z1), axis = 1)
  Yn = x0[1:].reshape((len(x0)-1, 1))
  [[a],[b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Yn) #计算参数
  f = lambda k: (x0[0]-b/a)*np.exp(-a*(k-1))-(x0[0]-b/a)*np.exp(-a*(k-2)) #还原值
  delta = np.abs(x0 - np.array([f(i) for i in range(1,len(x0)+1)]))
  C = delta.std()/x0.std()
  P = 1.0*(np.abs(delta - delta.mean()) < 0.6745*x0.std()).sum()/len(x0)
  return f, a, b, x0[0], C, P #返回灰色预测函数、a、b、首项、方差比、小残差概率

#-*- coding: utf-8 -*-
import numpy as np
import pandas as pd
from GM11 import GM11 #引入自己编写的灰色预测函数

inputfile = '../data/data1.csv' #输入的数据文件
outputfile = '../tmp/data1_GM11.xls' #灰色预测后保存的路径
data = pd.read_csv(inputfile) #读取数据
data.index = range(1994, 2014)

data.loc[2014] = None
data.loc[2015] = None
l = ['x1', 'x2', 'x3', 'x4', 'x5', 'x7']
for i in l:
  f = GM11(data[i][range(1994, 2014)].as_matrix())[0]
  data[i][2014] = f(len(data)-1) #2014年预测结果
  data[i][2015] = f(len(data)) #2015年预测结果
  data[i] = data[i].round(2) #保留两位小数

data[l+['y']].to_excel(outputfile) #结果输出

将数据零均值标准化后，代入地方财政收入所建立的三层神经网络预测模型（输入层6节点，隐藏层12节点，输出层1节点），得到某市财政收入2015年的预测值为2366.42亿元。

#-*- coding: utf-8 -*-
import pandas as pd
inputfile = '../tmp/data1_GM11.xls' #灰色预测后保存的路径
outputfile = '../data/revenue.xls' #神经网络预测后保存的结果
modelfile = '../tmp/1-net.model' #模型保存路径
data = pd.read_excel(inputfile) #读取数据
feature = ['x1', 'x2', 'x3', 'x4', 'x5', 'x7'] #特征所在列

data_train = data.loc[range(1994,2014)].copy() #取2014年前的数据建模
data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train - data_mean)/data_std #数据标准化
x_train = data_train[feature].as_matrix() #特征数据
y_train = data_train['y'].as_matrix() #标签数据

from keras.models import Sequential
from keras.layers.core import Dense, Activation

model = Sequential() #建立模型
model.add(Dense(6, 12))
model.add(Activation('relu')) #用relu函数作为激活函数，能够大幅提供准确度
model.add(Dense(12, 1))
model.compile(loss='mean_squared_error', optimizer='adam') #编译模型
model.fit(x_train, y_train, nb_epoch = 10000, batch_size = 16) #训练模型，学习一万次
model.save_weights(modelfile) #保存模型参数

#预测，并还原结果。
x = ((data[feature] - data_mean[feature])/data_std[feature]).as_matrix()
data[u'y_pred'] = model.predict(x) * data_std['y'] + data_mean['y']
data.to_excel(outputfile)

import matplotlib.pyplot as plt #画出预测结果图
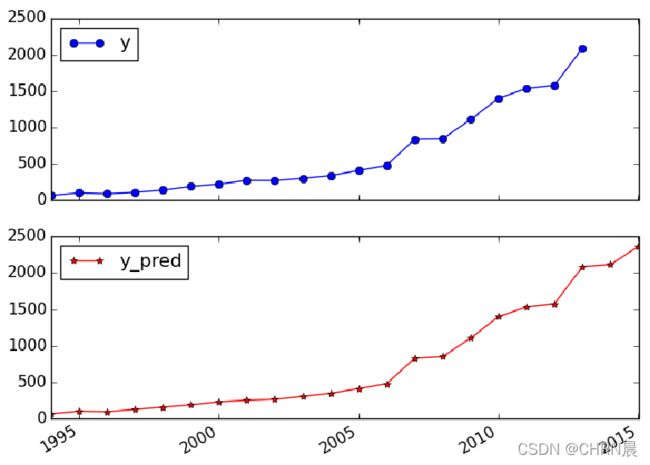
p = data[['y','y_pred']].plot(subplots = True, style=['b-o','r-*'])
plt.show()

  同时得到地方财政收入真实值与预测值对比图。

其它类别的收入分析过程也是一样的，这里就不一 一实现了