《Pytorch深度学习》学习记录
纯小白(python和深度学习都是),课程是《PyTorch深度学习实践》完结合集在此随便做一些随笔,由于前面学过一些机器学习,跳过前面的较基础知识直接从Pytorch实现线性回归开始
顺带一提本人使用的PyTorch版本是1.13.0
文章目录
- 线性回归知识回顾
- 本课内容
-
- 模型设计
- 损失函数和优化器
- 训练
- 完整代码(包含课后作业)
- 参考资料
线性回归知识回顾
线性回归在前面的课程中有讲这里不多做赘述,线性回归实际上就是在在超平面中画出一个超平面并且使得这个超平面的损失函数最小。
具体过程为通过前向传播算出loss值,之后用求出的loss对权重进行求导( ∂ L ∂ w \frac{\partial L}{\partial w} ∂w∂L)求出梯度(该步使用反向传播),最后根据梯度更新权重( w ′ = w − α ∗ ∂ L ∂ w w'=w- \alpha*\frac{\partial L}{\partial w} w′=w−α∗∂w∂L).反复迭代上述过程直至收敛。
本课内容
讲一下本课提到的几个术语:
minibatch(小批量):之前的梯度下降可以看到我们会对每一个数据求一次loss进行梯度下降,这个方法显而易见会在数据量巨大的时候处理困难。小批量的处理则是一次性处理多组数据,对loss进行平均而后梯度下降。
模型设计
import torch
class LinearModel(torch.nn.Module):
def __init__(self):
super(LinearModel,self).__init__()
self.linear=torch.nn.Linear(1,1)
def forward(self,x):
y_pred=self.linear(x)
return y_pred
model=LinearModel()
以上代码片是设计模型的一个简单模板。
根据官方文档Module类是所有神经网络模块的基类,Module可以以树形结构包含其他的Module。因此在设计自己的网络时需要继承该类,同时必须实现__init__()和forward()方法。不需要backward()方法的原因是用module构造出来的对象会自动完成该操作。对Module类的简单介绍可以看这个
上述代码片中还用到了nn.Linear,这里摘录PyTorch中文文档的说明,能对这个类有更清楚的认识
class torch.nn.Linear(in_features, out_features, bias=True)
对输入数据做线性变换:y=Ax+b
参数:
in_features - 每个输入样本的大小
out_features - 每个输出样本的大小
bias - 若设置为False,这层不会学习偏置。默认值:True
形状:
输入: (N,in_features)
输出: (N,out_features)
N是样本数
变量:
weight -形状为(out_features x in_features)的模块中可学习的权值
bias -形状为(out_features)的模块中可学习的偏置
损失函数和优化器
criterion=torch.nn.MSELoss(size_average=False)#相当于torch.nn.MSELoss(reduction='sum')
optimizer=torch.optim.SGD(model.parameters(),lr=0.01)
这里也摘录一下官方文档的说明(百度到的PyTorch的中文文档似乎已经太老了,和官方文档出入挺大的):
CLASStorch.nn.MSELoss(size_average=None, reduce=None, reduction=‘mean’)
用于计算输入值与目标值的均方误差
未简化loss(比如将reducton设为’none’)的定义:
l ( x , y ) = L = l 1 , . . . l N T , l n = ( x n − y n ) 2 l(x,y)=L={l_1,...l_N}^T,l_n=(x_n-y_n)^2 l(x,y)=L=l1,...lNT,ln=(xn−yn)2
其中N是batch的大小。如果reduction不为none(默认为mean),那么loss的定义为:
l ( x , y ) = { m e a n ( L ) , if reduction=’mean’ s u m ( L ) , if reduction=’sum’ l(x,y)=\begin{cases} mean(L),&\text {if reduction='mean'}\\ sum(L),&\text {if reduction='sum'} \end{cases} l(x,y)={mean(L),sum(L),if reduction=’mean’if reduction=’sum’
x,y是含有n个元素的任意形状的张量
mean操作会作用与所有元素上并除以n
将reduction设定为sum能避免除n的操作
参数:
size_average(bool, optional) - 在1.13.0中被废弃了(使用该参数依然可行,运行会跳warning)
reduce(bool, optional) - 在1.13.0中被废弃了(使用该参数依然可行,运行会跳warning)
reduction(string, optional) - 指定应用于输出的简化(或者说降维)方式,有三类('none'|'mean'|'sum')。使用size_average和reduce会被重写为reduction。reduction的默认值为“mean0’
形状:
输入值(*): 任意维度
目标值(*):和输入值同维度
可以看到nn.MSELoss也是一个callable的类
接下来是优化器SGD
CLASStorch.optim.SGD(params, lr=< required parameter>, momentum=0, dampening=0, weight_decay=0, nesterov=False)
参数:
params(iterable)-用于优化的可迭代参数或者已定义的字典型的参数
lr(float)-学习率
momentum (float, optional) –动量因子 (默认为0)
weight_decay (float, optional) – 权重衰减(L2 penalty) (默认为0)
dampening (float, optional) – 动量阻尼 (默认为0)
nesterov (bool, optional) –启用nesterov动量 (默认为False)
除了lr这个”步长“之外还能看到有许多其他的参数,不过目前为止还没有学到,就不做深入了。值得一提的是代码片中使用model.parameters()去找参数,是一个相当便利的方法。
训练
for epoch in range(100):
y_pred=model(x_data)
loss=criterion1(y_pred,y_data)
print(epoch,loss.item())
optimizer.zero_grad()
loss.backward()#反向传播
optimizer.step()#单步优化步
这块代码没有什么好说的,需要注意的是我们需要将优化器中的梯度手动地归零,这是由于backward()会将之前计算出来的梯度积累下来,在本次课程中我们显然不需要这么做。
完整代码(包含课后作业)
import torch
import numpy as np
import matplotlib.pyplot as plt
x_data=torch.Tensor([[1.0],[2.0],[3.0]])
y_data=torch.Tensor([[2.0],[4.0],[6.0]])
class LinearModel(torch.nn.Module):
def __init__(self):
super(LinearModel,self).__init__()
self.linear=torch.nn.Linear(1,1)
def forward(self,x):
y_pred=self.linear(x)
return y_pred
model=LinearModel()#实例化
criterion=torch.nn.MSELoss(size_average=False)
optimizer=torch.optim.SGD(model.parameters(),lr=0.01)
epochs=[]
losses=[]
for epoch in range(100):
y_pred=model(x_data)
loss=criterion1(y_pred,y_data)
print(epoch,loss.item())
epochs.append(epoch)
losses.append(loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()#更新
print('w=',model.linear.weight.item())
print('b=',model.linear.bias.item())
x_test=torch.Tensor([[4.0]])
y_test=model(x_test)
print('y_pred=',y_test.data)
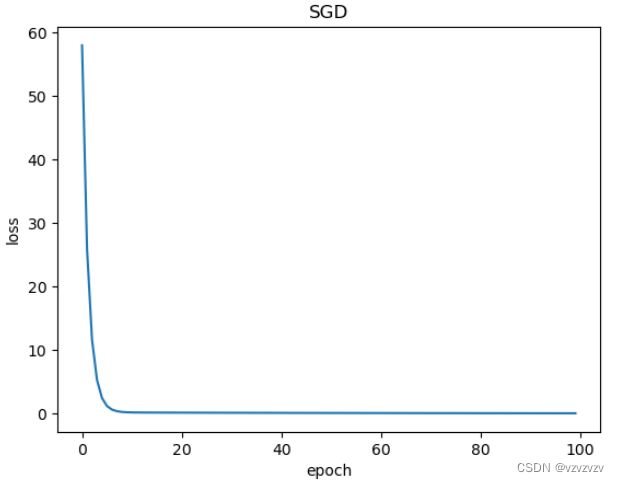
plt.plot(epochs,losses)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.title('SGD')
plt.show()
参考资料
Pytorch文档
Pytorch中文文档(文章内说这个文档过时了但我没找到与之一致的过往英文版本,但也有些内容是与英文版一致的还是值得看的)