机器学习 --- kNN算法
目录
第一关:实现KNN算法:
任务描述:
相关知识:
一、KNN算法的算法流程:
二、KNN算法的优缺点:
编程要求:
测试说明:
第二关:红酒分类:
任务描述:
相关知识:
一、数据集介绍:
二、StandardScaler的使用:
三、KNeighborsClassifier的使用:
编程要求:
测试说明:
第一关:实现KNN算法:
任务描述:
本关任务:补充 python 代码,完成 kNNClassifier 类中的 fit 函数与 predict 函数。实现 kNN 算法的训练与预测功能。
相关知识:
为了完成本关任务,你需要掌握 kNN 算法的算法流程。
一、KNN算法的算法流程:
kNN 算法其实是众多机器学习算法中最简单的一种,因为该算法的思想完全可以用 8 个字来概括:“近朱者赤,近墨者黑”。
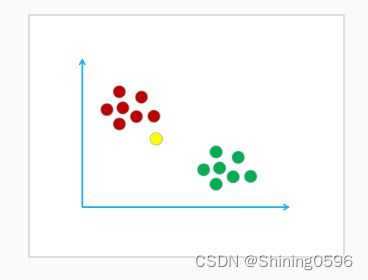
假设现在有这样的一个样本空间,该样本空间里有宅男和文艺青年这两个类别,其中红圈表示宅男,绿圈表示文艺青年。如下图所示:
其实构建出这样的样本空间的过程就是 kNN 算法的训练过程。可想而知 kNN 算法是没有训练过程的,所以 kNN 算法属于懒惰学习算法。
假设我在这个样本空间中用黄圈表示,如下图所示:
现在使用 kNN 算法来鉴别一下我是宅男还是文艺青年。首先需要计算我与样本空间中所有样本的距离。假设计算得到的距离表格如下:
| 样本编号 | 1 | 2 | ... | 13 | 14 |
|---|---|---|---|---|---|
| 标签 | 宅男 | 宅男 | ... | 文艺青年 | 文艺青年 |
| 距离 | 11.2 | 9.5 | ... | 23.3 | 37.6 |
然后找出与我距离最小的 k 个样本(k 是一个超参数,需要自己设置,一般默认为 5),假设与我离得最近的 5 个样本的标签和距离如下:
| 样本编号 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|
| 标签 | 宅男 | 宅男 | 宅男 | 宅男 | 文艺青年 |
| 距离 | 11.2 | 9.5 | 7.7 | 5.8 | 15.2 |
最后只需要对这 5 个样本的标签进行统计,并将票数最多的标签作为预测结果即可。如上表中,宅男是 4 票,文艺青年是 1 票,所以我是宅男。
注意:有的时候可能会有票数一致的情况,比如 k=4 时与我离得最近的样本如下:
| 样本编号 | 4 | 9 | 11 | 13 |
|---|---|---|---|---|
| 标签 | 宅男 | 宅男 | 文艺青年 | 文艺青年 |
| 距离 | 4.2 | 9.5 | 7.7 | 5.8 |
可以看出宅男和文艺青年的比分是 2:2,那么可以尝试将属于宅男的 2 个样本与我的总距离和属于文艺青年的 2 个样本与我的总距离进行比较。然后选择总距离最小的标签作为预测结果。在这个例子中预测结果为文艺青年(宅男的总距离为 4.2+9.5,文艺青年的总距离为 7.7+5.8)。
二、KNN算法的优缺点:
从算法流程中可以看出,kNN 算法的优点有:
- 原理简单,实现简单;
- 天生支持多分类,不像其他二分类算法在进行多分类时要使用 OvO、 OvR 的策略。
缺点也很明显:
- 当数据量比较大或者数据的特征比较多时,预测过程的时间效率太低。
编程要求:
根据提示,在右侧编辑器的 begin-end 区域补充代码,完成 kNNClassifier 类中的 fit 函数与 predict 函数。
fit 函数用于 kNN 算法的训练过程,其中:
-
feature :训练集数据,类型为 ndarray;
-
label :训练集标签,类型为 ndarray。
predict 函数用于实现 kNN 算法的预测过程,函数返回预测的标签,其中:
-
feature :测试集数据,类型为 ndarray。(PS:feature中有多条数据)
测试说明:
只需完成 fit 与 predict 函数即可,程序内部会调用您所完成的 fit 函数构建模型并调用 predict 函数来对数据进行预测。预测的准确率高于 0.9 视为过关。
#encoding=utf8
import numpy as np
class kNNClassifier(object):
def __init__(self, k):
'''
初始化函数
:param k:kNN算法中的k
'''
self.k = k
# 用来存放训练数据,类型为ndarray
self.train_feature = None
# 用来存放训练标签,类型为ndarray
self.train_label = None
def fit(self, feature, label):
'''
kNN算法的训练过程
:param feature: 训练集数据,类型为ndarray
:param label: 训练集标签,类型为ndarray
:return: 无返回
'''
#********* Begin *********#
self.train_feature = np.array(feature)
self.train_label = np.array(label)
#********* End *********#
def predict(self, feature):
'''
kNN算法的预测过程
:param feature: 测试集数据,类型为ndarray
:return: 预测结果,类型为ndarray或list
'''
#********* Begin *********#
def _predict(test_data):
distances = [np.sqrt(np.sum((test_data - vec) ** 2)) for vec in self.train_feature]
nearest = np.argsort(distances)
topK = [self.train_label[i] for i in nearest[:self.k]]
votes = {}
result = None
max_count = 0
for label in topK:
if label in votes.keys():
votes[label] += 1
if votes[label] > max_count:
max_count = votes[label]
result = label
else:
votes[label] = 1
if votes[label] > max_count:
max_count = votes[label]
result = label
return result
predict_result = [_predict(test_data) for test_data in feature]
return predict_result
#********* End *********#第二关:红酒分类:
任务描述:
本关任务: sklearn 中的 KNeighborsClassifier 类实现了 kNN 算法的分类功能,本关你需要使用 sklearn 中 KNeighborsClassifier 来对红酒数据进行分类。
相关知识:
为了完成本关任务,你需要掌握:
- StandarScaler 的使用;
- KNeighborsClassifier 的使用。
一、数据集介绍:
数据集为一份红酒数据,总共有 178 个样本,每个样本有 13 个特征,这里不会为你提供红酒的标签,你需要自己根据这 13 个特征对红酒进行分类。部分数据如下图:
二、StandardScaler的使用:
由于数据中有些特征的标准差比较大,例如 Proline 的标准差大约为 314。如果现在用 kNN 算法来对这样的数据进行分类的话, kNN 算法会认为最后一个特征比较重要。因为假设有两个样本的最后一个特征值分别为 1 和 100,那么这两个样本之间的距离可能就被这最后一个特征决定了。这样就很有可能会影响 kNN 算法的准确度。为了解决这种问题,我们可以对数据进行标准化。
标准化的手段有很多,而最为常用的就是 Z Score 标准化。Z Score 标准化通过删除平均值和缩放到单位方差来标准化特征,并将标准化的结果的均值变成 0 ,标准差为 1。
sklearn 中已经提供了 Z Score 标准化的接口 StandardScaler,使用代码如下:
from sklearn.preprocessing import StandardScaler
data = [[0, 0], [0, 0], [1, 1], [1, 1]]
# 实例化StandardScaler对象
scaler = StandardScaler()
# 用data的均值和标准差来进行标准化,并将结果保存到after_scaler
after_scaler = scaler.fit_transform(data)
# 用刚刚的StandardScaler对象来进行归一化
after_scaler2 = scaler.transform([[2, 2]])
print(after_scaler)
print(after_scaler2)打印结果如下:
[[-1. -1.][-1. -1.][ 1. 1.][ 1. 1.]][[3. 3.]]
根据打印结果可以看出,经过准换后,数据已经缩放成了均值为 0,标准差为1的分布。
三、KNeighborsClassifier的使用:
想要使用 sklearn 中使用 kNN 算法进行分类,只需要如下的代码(其中 train_feature、train_label 和 test_feature 分别表示训练集数据、训练集标签和测试集数据):
from sklearn.neighbors import KNeighborsClassifier
#生成K近邻分类器
clf=KNeighborsClassifier()
#训练分类器
clf.fit(train_feature, train_label)
#进行预测
predict_result=clf.predict(test_feature)但是当我们需要调整 kNN 算法的参数时,上面的代码就不能满足我的需求了。这里需要做的改变在clf=KNeighborsClassifier()这一行中。
KNeighborsClassifier() 的构造函数包含一些参数的设定。比较常用的参数有以下几个:
- n_neighbors :即 kNN 算法中的 K 值,为一整数,默认为 5;
- metric :距离函数。参数可以为字符串(预设好的距离函数)或者是callable对象。默认值为闵可夫斯基距离;
- p :当 metric 为闵可夫斯基距离公式时可用,为一整数,默认值为 2,也就是欧式距离。
编程要求:
根据提示,在右侧编辑器的 begin-end 间补充代码,完成 classification 函数。函数需要完成的功能是使用 KNeighborsClassifier 对 test_feature 进行分类。其中函数的参数如下:
-
train_feature : 训练集数据,类型为 ndarray;
-
train_label : 训练集标签,类型为 ndarray;
-
test_feature : 测试集数据,类型为 ndarray。
测试说明:
平台会对你返回的预测结果来计算准确率,你只需完成 classification 函数即可。准确率高于 0.9 视为过关。
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
def classification(train_feature, train_label, test_feature):
'''
对test_feature进行红酒分类
:param train_feature: 训练集数据,类型为ndarray
:param train_label: 训练集标签,类型为ndarray
:param test_feature: 测试集数据,类型为ndarray
:return: 测试集数据的分类结果
'''
#********* Begin *********#
scaler=StandardScaler()
train_feature=scaler.fit_transform(train_feature)
test_feature=scaler.transform(test_feature)
clf=KNeighborsClassifier()
clf.fit(train_feature,train_label)
return clf.predict(test_feature)
#********* End **********#