【Python量化】蒙特卡洛模拟法预测股价走势
文章目录
- 蒙特卡罗模拟法的定义
- 蒙特卡罗模拟法的的Python实现
-
- 蒙特卡洛模拟法模拟股票收益率序列
- 蒙特卡洛模拟法模拟股价序列
- 蒙特卡洛模拟法绘制模拟股价序列图
蒙特卡罗模拟法的定义
基本思想:蒙特卡罗模拟法(Monte Carlo Simulation, MCS)是在一定的统计分布假设下模拟风险因子的变化情况。首先假设资产收益为某一随机过程,并根据所设定的价格变动过程,大量模拟未来各种可能发生的情境,然后将某一情境下投资组合变化值排序,给出投资组合变化的分布,据此就可以估算不同置信水平下的VaR值。
基本步骤:
每一次蒙特卡洛模拟,对资产组合中的每一资产按照随机过程公式模拟出下一个交易日的价格,公式中的ε可以假定服从t分布或正态分布(即资产收益率服从的分布),然后可以得到每一资产的收益率,乘以各自的权重和市值就能得到每一资产在下一个交易日的收益,全部相加就是该资产组合在下一个交易日的模拟收益。
假设股票价格符合几何布朗运动,即
d S t = μ t S t d t + σ t S t d W t dS_t=\mu_tS_tdt+\sigma_tS_tdW_t dSt=μtStdt+σtStdWt
简化处理,得到特定时期(0,T)资产价格变化过程:
Δ S t = S t ( μ Δ t + σ ε t Δ t ) , t = 1 , 2 , . . . , N , N Δ t = T \Delta S_t=S_t(\mu\Delta t+\sigma\varepsilon_t\sqrt{\Delta t}),t=1,2,...,N,N\Delta t=T ΔSt=St(μΔt+σεtΔt),t=1,2,...,N,NΔt=T
于是得到:
S t + 1 = S t + S t ( μ Δ t + σ ε t Δ t ) , t = 1 , 2 , . . . , N , N Δ t = T S_{t+1}=S_t+S_t(\mu\Delta t+\sigma\varepsilon_t\sqrt{\Delta t}),t=1,2,...,N,N\Delta t=T St+1=St+St(μΔt+σεtΔt),t=1,2,...,N,NΔt=T
也可表示为:
S t + 1 = S t e ( μ − σ 2 2 ) Δ t + σ ε t Δ t S_{t+1}=S_te^{(\mu-\frac{\sigma^2}2)\Delta t+\sigma\varepsilon_t\sqrt{\Delta t}} St+1=Ste(μ−2σ2)Δt+σεtΔt
其中 μ \mu μ为收益率均值, σ 2 \sigma^2 σ2为收益率方差, ε \varepsilon ε服从t分布或正态分布。
则收益率为:
r e t u r n = ( μ − σ 2 2 ) d t + σ ε t d t return=(\mu-\frac{\sigma^2}2)dt+\sigma\varepsilon_t\sqrt{dt} return=(μ−2σ2)dt+σεtdt
蒙特卡罗模拟法的的Python实现
蒙特卡洛模拟法模拟股票收益率序列
收益率为:
r e t u r n = ( μ − σ 2 2 ) d t + σ ε t d t return=(\mu-\frac{\sigma^2}2)dt+\sigma\varepsilon_t\sqrt{dt} return=(μ−2σ2)dt+σεtdt
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import pandas as pd
import math
'''
s:股票现价
t:期限(年)
r:股票年化收益率
sigma:股票年化波动率
nper_per_year:每年的期数
'''
def generate_simulated_stock_returns(t,r,sigma,nper_per_year):
simulated_returns=[]
dt=1/nper_per_year
term = int(t*nper_per_year)
for i in range (1, term+1):
z=np.random.normal()
simulated_return = (r-(sigma**2/2))*dt + z*sigma*(dt**(1/2))
simulated_returns.append(simulated_return)
array_return=np.array(simulated_returns)
return array_return
# 初始股价s:100; 预期收益率r:10%;标准差:30%
s=100;r=0.1;sigma=0.3
#1年期、每年2期
t=1;nper_per_year=2
array_return = generate_simulated_stock_returns(t,r,sigma,nper_per_year)
print(array_return)
#2年期、每年24期
t=2;nper_per_year=24
array_return = generate_simulated_stock_returns(t,r,sigma,nper_per_year)
print(array_return)
[ 0.21738696 -0.06383675]
[ 0.02899686 0.00131385 -0.09489962 -0.00440415 -0.0357566 -0.05227566
0.07905745 -0.03065636 -0.01726008 -0.0059791 0.05072394 0.01448947
0.03098366 -0.05170335 0.0161574 -0.18380967 -0.0629412 0.00289641
0.14890079 -0.05693315 0.0931597 0.0037413 -0.05493882 0.12309281
0.06119329 0.04241972 -0.02030099 -0.05180438 -0.05970102 0.0229074
0.12618542 0.0770313 0.05075201 -0.04261307 0.00168359 0.03529421
0.0850315 -0.09281302 -0.08985412 0.02220526 0.01642511 0.04967819
0.07372143 -0.01799848 0.05595597 -0.00384655 -0.09679426 -0.08459783]
蒙特卡洛模拟法模拟股价序列
股价为:
S i = S i − 1 × e r i − 1 S_i = S_{i-1} \times e^{r_{i-1}} Si=Si−1×eri−1
def generate_simulated_stock_values(s,t,r,sigma,nper_per_year):
rate=generate_simulated_stock_returns(t,r,sigma,nper_per_year)
stock_price = [s]
term = int(t*nper_per_year)
for i in range(1, term+1):
values = stock_price[i-1]*math.e**(rate[i-1])
stock_price.append(values)
array_price = np.array(stock_price)
return array_price
#1年期、每年2期
t=1;nper_per_year=2
array_price = generate_simulated_stock_values(s,t,r,sigma,nper_per_year)
print(array_price)
#2年期、每年24期
t=2;nper_per_year=24
array_price = generate_simulated_stock_values(s,t,r,sigma,nper_per_year)
print(array_price)
[100. 105.03146796 100.4594981 ]
[100. 95.90978914 95.65450188 104.70632493 102.12337933
104.26726892 99.06536039 100.63054422 93.6685905 88.57596138
92.41510048 89.91265499 86.27490259 87.29911775 84.26798089
86.5798334 87.06325173 87.61229376 81.72201584 85.49976969
82.96816113 80.11385795 83.01588423 77.73720797 72.770712
63.60523084 65.39745198 69.02682262 67.64864604 62.52653157
61.57041633 58.01208479 62.16882528 66.41108904 66.4236716
59.67428405 68.38557448 70.2657609 75.26920257 77.15860959
80.52151818 74.45625968 71.23642008 70.7874225 69.68587971
75.54529952 67.20571691 67.86359575 67.393064 ]
蒙特卡洛模拟法绘制模拟股价序列图
def plot_simulated_stock_values(s,t,r,sigma,nper_per_year,num_trials=1):
term = int(t*nper_per_year) + 1
x_axis = np.linspace(0,t,term)
for i in range(num_trials):
price=generate_simulated_stock_values(s,t,r,sigma,nper_per_year)
plt.plot(x_axis, price)
plt.title(str(num_trials)+" simulated trials")
plt.xlabel("years")
plt.ylabel("value")
plt.show()
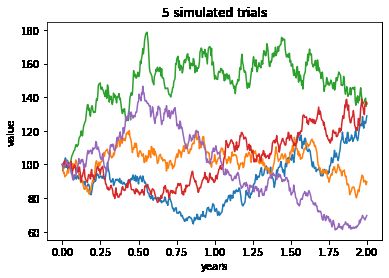
# 2年期、每年250期,模拟5次
t=2;nper_per_year=250;num_trials=5
plot_simulated_stock_values(s,t,r,sigma,nper_per_year,num_trials)
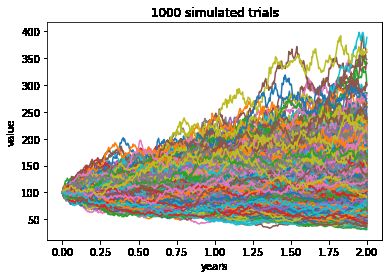
# 2年期、每年250期,模拟1000次
t=2;nper_per_year=250;num_trials=1000
plot_simulated_stock_values(s,t,r,sigma,nper_per_year,num_trials)