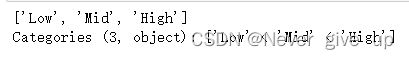第九章 分类数据
文章目录
- 一、cat对象
-
- 1. cat对象的属性
- 2. 类别的增加、删除和修改
- 二、有序分类
-
- 1. 序的建立
- 2. 排序和比较
- 三、区间类别
-
- 1. 利用cut和qcut进行区间构造
- 2. 一般区间的构造
- 3. 区间的属性与方法
- 四、练习
-
- Ex1:统计未出现的类别
- Ex2:钻石数据集
import numpy as np
import pandas as pd
一、cat对象
1. cat对象的属性
在pandas中提供了category类型,使用户能够处理分类类型的变量,将一个普通序列转换成分类变量可以使用astype方法。
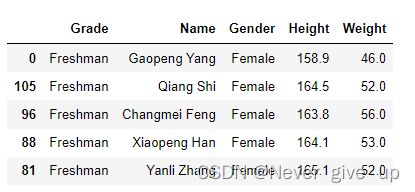
df = pd.read_csv('../data/learn_pandas.csv', usecols = ['Grade', 'Name', 'Gender', 'Height', 'Weight'])
s = df.Grade.astype('category')
s.head()

在一个分类类型的Series中定义了cat对象,它和上一章中介绍的str对象类似,定义了一些属性和方法来进行分类类别的操作。
s.cat
![]()
对于一个具体的分类,有两个组成部分,其一为类别的本身,它以Index类型存储,其二为是否有序,它们都可以通过cat的属性被访问:
s.cat.categories
s.cat.ordered
![]()
另外,每一个序列的类别会被赋予唯一的整数编号,它们的编号取决于cat.categories中的顺序,该属性可以通过codes访问:
s.cat.codes.head()
2. 类别的增加、删除和修改
通过cat对象的categories属性能够完成对类别的查询,那么应该如何进行“增改查删”的其他三个操作呢?
【NOTE】类别不得直接修改
在第三章中曾提到,索引 Index 类型是无法用 index_obj[0] = item 来修改的,而 categories 被存储在 Index 中,因此 pandas 在 cat 属性上定义了若干方法来达到相同的目的。
首先,对于类别的增加可以使用add_categories:
s = s.cat.add_categories('Graduate') # 增加一个毕业生类别
s.cat.categories
![]()
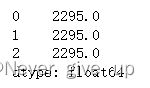
若要删除某一个类别可以使用remove_categories,同时所有原来序列中的该类会被设置为缺失。例如,删除大一的类别:
s = s.cat.remove_categories('Freshman')
s.cat.categories
s.head()

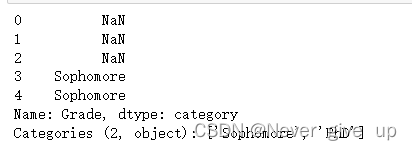
此外可以使用set_categories直接设置序列的新类别,原来的类别中如果存在元素不属于新类别,那么会被设置为缺失。
s = s.cat.set_categories(['Sophomore','PhD']) # 新类别为大二学生和博士
s.cat.categories
s.head()
如果想要删除未出现在序列中的类别,可以使用remove_unused_categories来实现:
s = s.cat.remove_unused_categories() # 移除了未出现的博士生类别
s.cat.categories
![]()
最后,“增改查删”中还剩下修改的操作,这可以通过rename_categories方法完成,同时需要注意的是,这个方法会对原序列的对应值也进行相应修改。例如,现在把Sophomore改成中文的本科二年级学生:
s = s.cat.rename_categories({'Sophomore':'本科二年级学生'})
s.head()
二、有序分类
1. 序的建立
有序类别和无序类别可以通过as_unordered和reorder_categories互相转化,需要注意的是后者传入的参数必须是由当前序列的无序类别构成的列表,不能够增加新的类别,也不能缺少原来的类别,并且必须指定参数ordered=True,否则方法无效。例如,对年级高低进行相对大小的类别划分,然后再恢复无序状态:
s = df.Grade.astype('category')
s = s.cat.reorder_categories(['Freshman', 'Sophomore', 'Junior', 'Senior'],ordered=True)
s.head()
s.cat.as_unordered().head()

【NOTE】类别不得直接修改
如果不想指定ordered=True参数,那么可以先用s.cat.as_ordered()转化为有序类别,再利用reorder_categories进行具体的相对大小调整。
2. 排序和比较
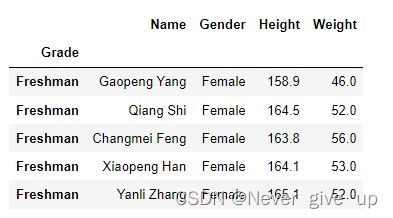
在第二章中,曾提到了字符串和数值类型序列的排序,此时就要说明分类变量的排序:只需把列的类型修改为category后,再赋予相应的大小关系,就能正常地使用sort_index和sort_values。例如,对年级进行排序:
df.Grade = df.Grade.astype('category')
df.Grade = df.Grade.cat.reorder_categories(['Freshman', 'Sophomore', 'Junior', 'Senior'],ordered=True)
df.sort_values('Grade').head() # 值排序
df.set_index('Grade').sort_index().head() # 索引排序
由于序的建立,因此就可以进行比较操作。分类变量的比较操作分为两类,第一种是==或!=关系的比较,比较的对象可以是标量或者同长度的Series(或list),第二种是>,>=,<,<=四类大小关系的比较,比较的对象和第一种类似,但是所有参与比较的元素必须属于原序列的categories,同时要和原序列具有相同的索引。
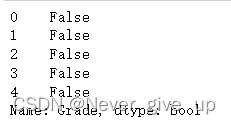
res1 = df.Grade == 'Sophomore'
res1.head()
res2 = df.Grade == ['PhD']*df.shape[0]
res2.head()
res3 = df.Grade <= 'Sophomore'
res3.head()
res4 = df.Grade <= df.Grade.sample(frac=1).reset_index(drop=True) # 打乱后比较
res4.head()
三、区间类别
1. 利用cut和qcut进行区间构造
区间是一种特殊的类别,在实际数据分析中,区间序列往往是通过cut和qcut方法进行构造的,这两个函数能够把原序列的数值特征进行装箱,即用区间位置来代替原来的具体数值。
首先介绍cut的常见用法:
其中,最重要的参数是bins,如果传入整数n,则代表把整个传入数组的按照最大和最小值等间距地分为n段。由于区间默认是左开右闭,需要在调整时把最小值包含进去,在pandas中的解决方案是在值最小的区间左端点再减去0.001*(max-min),因此如果对序列[1,2]划分为2个箱子时,第一个箱子的范围(0.999,1.5],第二个箱子的范围是(1.5,2]。如果需要指定左闭右开时,需要把right参数设置为False,相应的区间调整方法是在值最大的区间右端点再加上0.001*(max-min)。
s = pd.Series([1,2])
pd.cut(s, bins=2)
pd.cut(s, bins=2, right=False)

bins的另一个常见用法是指定区间分割点的列表(使用np.infty可以表示无穷大):
pd.cut(s, bins=[-np.infty, 1.2, 1.8, 2.2, np.infty])

另外两个常用参数为labels和retbins,分别代表了区间的名字和是否返回分割点(默认不返回):
s = pd.Series([1,2])
res = pd.cut(s, bins=2, labels=['small', 'big'], retbins=True)
res[0]
res[1] # 该元素为返回的分割点
![]()
从用法上来说,qcut和cut几乎没有差别,只是把bins参数变成的q参数,qcut中的q是指quantile。这里的q为整数n时,指按照n等分位数把数据分箱,还可以传入浮点列表指代相应的分位数分割点。
s = df.Weight
pd.qcut(s, q=3).head()
pd.qcut(s, q=[0,0.2,0.8,1]).head()
2. 一般区间的构造
对于某一个具体的区间而言,其具备三个要素,即左端点、右端点和端点的开闭状态,其中开闭状态可以指定right, left, both, neither中的一类:
my_interval = pd.Interval(0, 1, 'right')
my_interval
![]()
其属性包含了mid, length, right, left, closed,,分别表示中点、长度、右端点、左端点和开闭状态。
使用in可以判断元素是否属于区间:
0.5 in my_interval
![]()
使用overlaps可以判断两个区间是否有交集:
my_interval_2 = pd.Interval(0.5, 1.5, 'left')
my_interval.overlaps(my_interval_2)
![]()
一般而言,pd.IntervalIndex对象有四类方法生成,分别是from_breaks, from_arrays, from_tuples, interval_range,它们分别应用于不同的情况:
from_breaks的功能类似于cut或qcut函数,只不过后两个是通过计算得到的分割点,而前者是直接传入自定义的分割点:
pd.IntervalIndex.from_breaks([1,3,6,10], closed='both')

from_arrays是分别传入左端点和右端点的列表,适用于有交集并且知道起点和终点的情况:
pd.IntervalIndex.from_arrays(left = [1,3,6,10], right = [5,4,9,11], closed = 'neither')
pd.IntervalIndex.from_tuples([(1,5),(3,4),(6,9),(10,11)], closed='neither')

一个等差的区间序列由起点、终点、区间个数和区间长度决定,其中三个量确定的情况下,剩下一个量就确定了,interval_range中的start, end, periods, freq参数就对应了这四个量,从而就能构造出相应的区间:
pd.interval_range(start=1,end=5,periods=8)
pd.interval_range(end=5,periods=8,freq=0.5)

【练一练】
无论是interval_range还是下一章时间序列中的date_range都是给定了等差序列中四要素中的三个,从而确定整个序列。请回顾等差数列中的首项、末项、项数和公差的联系,写出interval_range中四个参数之间的恒等关系。
start + periods * freq = end
除此之外,如果直接使用pd.IntervalIndex([...], closed=...),把Interval类型的列表组成传入其中转为区间索引,那么所有的区间会被强制转为指定的closed类型,因为pd.IntervalIndex只允许存放同一种开闭区间的Interval对象。
my_interval
my_interval_2
pd.IntervalIndex([my_interval, my_interval_2], closed='left')
3. 区间的属性与方法
IntervalIndex上也定义了一些有用的属性和方法。同时,如果想要具体利用cut或者qcut的结果进行分析,那么需要先将其转为该种索引类型:
id_interval = pd.IntervalIndex(pd.cut(s, 3))
id_interval[:3]

与单个Interval类型相似,IntervalIndex有若干常用属性:left, right, mid, length,分别表示左右端点、两端点均值和区间长度。
id_demo = id_interval[:5] # 选出前5个展示
id_demo
id_demo.left
id_demo.right
![]()
id_demo.mid
id_demo.length

IntervalIndex还有两个常用方法,包括contains和overlaps,分别指逐个判断每个区间是否包含某元素,以及是否和一个pd.Interval对象有交集。
id_demo.contains(4)
![]()
id_demo.overlaps(pd.Interval(40,60))
![]()
四、练习
Ex1:统计未出现的类别
在第五章中介绍了crosstab函数,在默认参数下它能够对两个列的组合出现的频数进行统计汇总:
df = pd.DataFrame({'A':['a','b','c','a'], 'B':['cat','cat','dog','cat']})
pd.crosstab(df.A, df.B)

但事实上有些列存储的是分类变量,列中并不一定包含所有的类别,此时如果想要对这些未出现的类别在crosstab结果中也进行汇总,则可以指定dropna参数为False:
df.B = df.B.astype('category').cat.add_categories('sheep')
pd.crosstab(df.A, df.B, dropna=False)

请实现一个带有dropna参数的my_crosstab函数来完成上面的功能。
def my_crosstab(s1, s2, dropna=True):
idx1 = (s1.cat.categories if s1.dtype.name == 'category' and not dropna else s1.unique())
idx2 = (s2.cat.categories if s2.dtype.name == 'category' and not dropna else s2.unique())
res = pd.DataFrame(np.zeros((idx1.shape[0], idx2.shape[0])), index=idx1, columns=idx2)
for i, j in zip(s1, s2):
res.at[i, j] += 1
res = res.rename_axis(index=s1.name, columns=s2.name).astype('int')
return res
df = pd.DataFrame({'A':['a','b','c','a'], 'B':['cat','cat','dog','cat']})
df.B = df.B.astype('category').cat.add_categories('sheep')
my_crosstab(df.A, df.B)
my_crosstab(df.A, df.B, dropna=False)
Ex2:钻石数据集
现有一份关于钻石的数据集,其中carat, cut, clarity, price分别表示克拉重量、切割质量、纯净度和价格,样例如下:
df = pd.read_csv('../data/diamonds.csv')
df.head(3)
- 分别对
df.cut在object类型和category类型下使用nunique函数,并比较它们的性能。
df = pd.read_csv('../data/diamonds.csv')
s_obj, s_cat = df.cut, df.cut.astype('category')
%timeit -n 30 s_obj.nunique()
%timeit -n 30 s_cat.nunique()
![]()
- 钻石的切割质量可以分为五个等级,由次到好分别是
Fair, Good, Very Good, Premium, Ideal,纯净度有八个等级,由次到好分别是I1, SI2, SI1, VS2, VS1, VVS2, VVS1, IF,请对切割质量按照由好到次的顺序排序,相同切割质量的钻石,按照纯净度进行由次到好的排序。
df.cut = df.cut.astype('category').cat.reorder_categories(['Fair', 'Good', 'Very Good', 'Premium', 'Ideal'],ordered=True)
df.clarity = df.clarity.astype('category').cat.reorder_categories(['I1', 'SI2', 'SI1', 'VS2', 'VS1', 'VVS2', 'VVS1', 'IF'],ordered=True)
res = df.sort_values(['cut', 'clarity'], ascending=[False, True])
res.head(3)
res.tail(3)
- 分别采用两种不同的方法,把
cut, clarity这两列按照由好到次的顺序,映射到从0到n-1的整数,其中n表示类别的个数。
df.cut = df.cut.cat.reorder_categories(df.cut.cat.categories[::-1])
df.clarity = df.clarity.cat.reorder_categories(df.clarity.cat.categories[::-1])
df.cut = df.cut.cat.codes # 方法一:利用cat.codes
clarity_cat = df.clarity.cat.categories
df.clarity = df.clarity.replace(dict(zip(clarity_cat, np.arange(len(clarity_cat))))) # 方法二:使用replace映射
df.head(3)
- 对每克拉的价格分别按照分位数(q=[0.2, 0.4, 0.6, 0.8])与[1000, 3500, 5500, 18000]割点进行分箱得到五个类别
Very Low, Low, Mid, High, Very High,并把按这两种分箱方法得到的category序列依次添加到原表中。
q = [0, 0.2, 0.4, 0.6, 0.8, 1]
point = [-np.infty, 1000, 3500, 5500, 18000, np.infty]
avg = df.price / df.carat
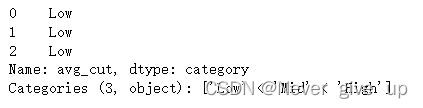
df['avg_cut'] = pd.cut(avg, bins=point, labels=['Very Low', 'Low', 'Mid', 'High', 'Very High'])
df['avg_qcut'] = pd.qcut(avg, q=q, labels=['Very Low', 'Low', 'Mid', 'High', 'Very High'])
df.head()
- 第4问中按照整数分箱得到的序列中,是否出现了所有的类别?如果存在没有出现的类别请把该类别删除。
df.avg_cut.unique()
df.avg_cut.cat.categories
df.avg_cut = df.avg_cut.cat.remove_categories(['Very Low', 'Very High'])
df.avg_cut.head(3)
- 对第4问中按照分位数分箱得到的序列,求每个样本对应所在区间的左右端点值和长度。
interval_avg = pd.IntervalIndex(pd.qcut(avg, q=q))
interval_avg.right.to_series().reset_index(drop=True).head(3)
interval_avg.left.to_series().reset_index(drop=True).head(3)
interval_avg.length.to_series().reset_index(drop=True).head(3)