Diffusion Models for Medical Image Analysis A Comprehensive Survey

Diffusion Models for Medical Image Analysis: A Comprehensive Survey

论文链接：[2211.07804] Diffusion Models for Medical Image Analysis: A Comprehensive Survey (arxiv.org)

GitHub链接：https://github.com/amirhossein-kz/Awesome-Diffusion-Models-in-Medical-Imaging

摘要

去噪扩散模型是一类生成模型，最近在各种深度学习问题中引起了极大的兴趣。扩散概率模型定义了前向扩散阶段，其中输入数据通过添加高斯噪声在几个步骤上被逐渐扰动。尽管扩散模型具有已知的计算负担，但其强大的模式覆盖率和生成的样本的质量被广泛赞赏。利用计算机视觉的进步，医学成像领域也观察到对扩散模型的兴趣越来越大。为了帮助研究者驾驭这一庞然大物，本次调查旨在全面概述医学图像分析学科中的扩散模型。具体而言，我们首先介绍了扩散模型和三种通用扩散建模框架（即扩散概率模型、噪声条件分数网络和随机微分方程）背后的坚实理论基础和基本概念。然后，我们提供了医学领域中扩散模型的系统分类，并提出了基于其应用、成像模式、感兴趣器官和算法的多视角分类。为此，我们涵盖了扩散模型在医学领域的广泛应用，包括分割、异常检测、图像到图像转换、2/3D生成、重建、去噪和其他医学相关挑战。此外，我们强调了一些选定方法的实际使用情况，然后讨论了医学领域中扩散模型的局限性，并提出了满足该领域需求的几个方向。

1. 介绍

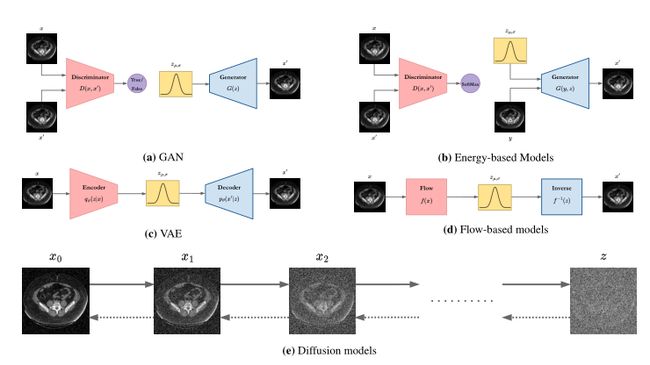
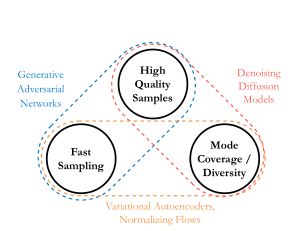
在过去十年的深度学习中，使用神经网络的生成建模一直是一股强大的力量。自产生以来，生成模型在从图像[5]、6]、音频[7、8]到文本[9]和点云[10]的各个领域产生了巨大影响。从概率建模的角度来看，生成模型的关键定义特征是它以这样的方式进行训练，使得其样本$x\sim p_{\theta }(x)$来自与训练数据分布相同的分布，$x\sim p_d(x)$​。开创性的基于能量的模型通过定义状态空间上的非标准化概率密度来实现这一点；然而，这些方法需要在训练和推理期间进行马尔可夫链蒙特卡罗（MCMC）采样，这是一个缓慢的迭代过程[11]。随着可用数据集的空前激增，以及一般深度学习架构的进步，生成建模出现了革命性的范式转变。具体而言，三种主流生成框架包括，即生成对抗网络（GAN）[1]、变分自动编码器（VAE）[12,3]和归一化流[13]（见图1）。生成模型通常需要在现实问题中采用关键需求。这些要求包括（i）高质量采样，（ii）模式覆盖和采样多样性，以及（iii）快速执行时间和计算成本低廉的采样[14]（见图2）。生成模型通常在这些标准之间进行调整。具体而言，GAN能够快速生成高质量的样本，但它们的模式覆盖率很低，并且容易缺乏采样多样性。相反，VAE和标准化流具有低样本质量的固有特性，尽管在覆盖数据模式中可以看到。GAN由两个模型组成：一个生成器和一个评论家（鉴别者），它们相互竞争，同时使彼此变得更强。生成器试图捕获真实示例的分布，而鉴别器（通常是二进制分类器）估计给定样本来自真实数据集的概率。它是一个评论家，经过优化，可以从真实样本中识别出合成样本。GAN的共同关注点是其训练动态这已经被认为是不稳定的，导致模式崩溃、消失梯度和收敛等缺陷[15]。因此，巨大的兴趣也影响了GAN提出更有效变体的研究方向[16，17]。V变量自动编码器（V AE）通过最大化证据下限（ELBO）来优化数据的对数似然性。尽管取得了显著的成就，但由于一些理论和实践挑战，如平衡问题[18]和变量崩溃现象[19]，V变量自动编码器的性能仍远不能令人满意。基于流的生成模型由一系列可逆变换构成。具体而言，标准化流程通过应用一系列可逆变换函数将简单分布转换为复杂分布，其中可以使用变量变化定理获得最终目标变量的期望概率分布。与GAN和V AE不同，这些模型明确学习数据分布；因此，它们的损失函数只是负对数似然[20]。尽管这些生成模型的设计是可行的，但它们有其特定的缺点。

由于基于可能性的方法必须构建标准化概率模型，因此必须使用特定类型的架构（自回归模型、流量模型），或者在V AE的情况下，不直接为生成的概率分布计算替代损失（如ELBO）。相反，由于GAN的对抗性损失的性质，GAN的学习过程本质上是不稳定的。最近，扩散模型[21，22]已成为强大的生成模型，展示了计算机视觉中的一个主要主题，因此研究人员和从业者可能会发现跟上创新速度是一个挑战。从根本上讲，扩散模型的工作原理是通过连续添加高斯噪声来破坏训练数据，然后学习通过反转这种噪声过程来恢复数据。

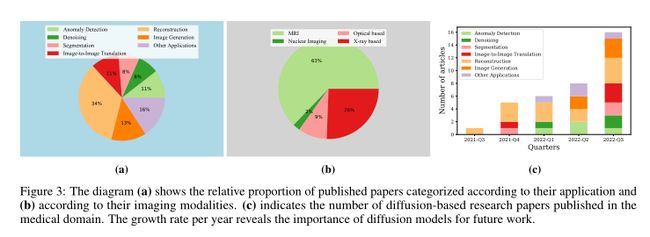
迄今为止，已经发现扩散模型在广泛的领域中是有用的，从生成建模任务（如图像生成[23]、图像超分辨率[24]、图像修复[25]）到辨别任务（如，图像分割[26]、分类[27]和异常检测[28]）。最近，医学成像界见证了基于扩散的技术数量的指数增长（见图3）。如图3所示，大量研究致力于扩散模型在不同医学成像场景中的应用。因此，对现有文献进行调查既有利于社区，也非常及时。为此，本调查旨在全面概述最近取得的进展，并全面概述医学成像中的这类模型。对相关文献的彻底搜索表明，我们是第一个涵盖医学领域中使用的基于扩散的模型的公司。我们希望这项工作将为研究人员指明新的路径，提供路线图，并激发视觉界的进一步兴趣，以利用医学领域中扩散模型的潜力。我们的主要贡献包括：

• 这是第一篇全面涵盖扩散模型在医学成像领域应用的调查论文。具体而言，我们对所有可用的相关论文进行了全面概述（截至2022年10月）。
• 我们设计了医学界扩散模型的多视角分类，提供了扩散模型及其应用研究的系统分类。我们将现有的扩散模型分为三类：去噪扩散概率模型、噪声条件分数网络和随机微分方程。
• 此外，我们将扩散模型的应用分为七类：异常检测、去噪、重建、分割、图像到图像的转换、图像生成和其他应用。
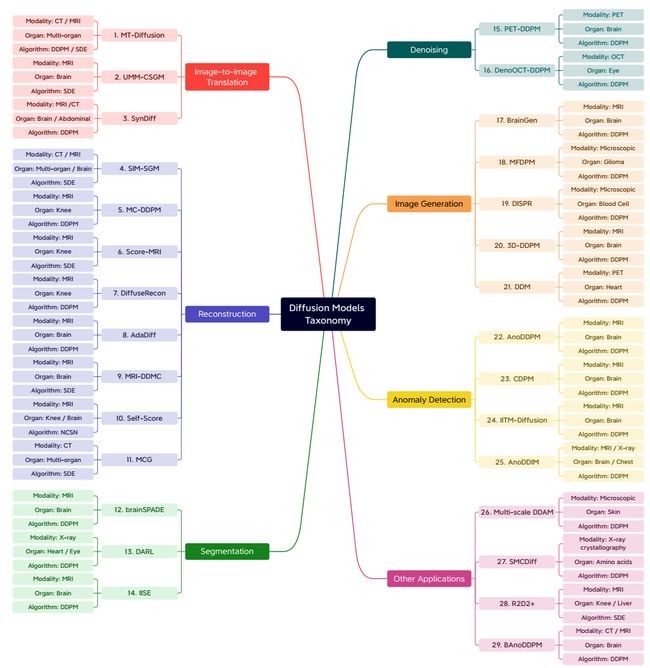
• 我们不将注意力局限于应用，并提供了一种新的分类法（见图4），其中每一篇论文都根据所提出的算法以及相关器官和成像模式进行了广泛分类。
• 最后，我们讨论了挑战和开放性问题，并确定了新的趋势，这些趋势提出了关于医学领域扩散模型在算法和应用方面未来发展的开放性问题。

2. Taxonomy

在过去几十年中，生成方法在医学成像方面取得了重大进展。因此，已经发表了许多关于医学成像深度生成模型的调查论文[29，30，31]。其中一些论文只关注特定的应用，而另一些则关注特定的图像模态。然而，缺乏关于扩散模型在医学成像中的应用的全面调查。为此，在本次调查中，我们设计了一个扩散模型的多视角视角，其中我们根据其在医学领域的应用讨论了现有文献。尽管如此，我们并不局限于应用，而是描述了所提出方法的基本工作原理、器官和成像模式。我们进一步讨论了这些附加信息如何帮助研究人员尝试整合整个光谱的文献。我们论文的简要展望如图4所示。

2.1 Algorithm

至少有三个子类别的扩散模型符合扩散模型的基线定义[60]。首先，有去噪扩散概率模型（DDPM）[21，22]，这是一类受非平衡热力学考虑启发的潜在变量模型。第二个子类别由噪声条件分数网络（NCSN）[61]表示，其基本上基于估计不同噪声水平下扰动数据分布的对数密度函数的导数。随机微分方程（SDEs）[62]形成了第三个子类别，它封装了以前的方法，可以被视为DDPM和NCSN的推广。我们将在下文详细阐述每一类的细节。

2.1.1 Denoising Diffusion Probabilistic Models (DDPMs)

Forward Process：DDPM将前向扩散过程定义为马尔可夫链，其中在连续步骤中添加高斯噪声以获得一组噪声样本。考虑$q(x_0)$作为未损坏（原始）数据分布。给定数据样本$x_0\sim q(x_0)$，通过在时间$t$添加高斯噪声产生潜在$x_1$到$x_T$的前向噪声处理$p$定义如下：
$$q\left(x_t\mid x_{t-1}\right)=\mathcal{N}\left(x_t;\sqrt{1-{\beta }_t}\cdot x_{t-1},{\beta }_t\cdot \mathbf{I}\right),\forall t\in \{1,\dots ,T\}\text{\hspace{1em}(1)}$$
其中$T$和${\beta }_1，\dots ，{\beta }_T\in [0，1)$分别表示扩散步骤的数量和扩散步骤之间的方差表。$I$是单位矩阵，$\mathcal{N}(x;\mu ,\sigma )$表示均值$\mu$和协方差$\sigma$的正态分布。考虑到${\alpha }_t=1-{\beta }_t$和${\alpha }_t=\prod _{s=0}^t{\alpha }_s$，可以直接对输入$x_0$上的噪声潜像的任意步骤进行采样，如下所示：

$$q\left({\mathbf{x}}_t\mid {\mathbf{x}}_0\right)=N\left({\mathbf{x}}_t;\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0,\left(1-{\bar{\alpha }}_t\right)\mathbf{I}\right)\text{\hspace{1em}(2)}$$

$${\mathrm{x}}_t=\sqrt{{\bar{\alpha }}_t}{\mathrm{x}}_0+\sqrt{1-\overline{{\alpha }_l}}ϵ\text{\hspace{1em}(3)}$$

Reverse Process：利用上述定义，我们可以近似逆过程从$q(x_0)$获得样本。为此，我们可以从$p(x_T)=\mathcal{N}(x_T;0,I)$开始参数化这个反向过程，如下所示：
$$p_{\theta }\left({\mathbf{x}}_{0:T}\right)=p\left({\mathbf{x}}_T\right)\prod _{t=1}^T{p}_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t\right)\text{\hspace{1em}(4)}$$

$$p_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t\right)=\mathcal{N}\left({\mathbf{x}}_{t-1};{\mu }_{\theta }\left({\mathbf{x}}_t,t\right),{\Sigma }_{\theta }\left({\mathbf{x}}_t,t\right)\right)\text{\hspace{1em}(5)}$$

为了训练该模型，使$p(x_0)$学习真实数据分布$q(x_0)$，我们可以优化负对数似然上的以下变分界限：
$$\begin{array}{rl}\mathbb{E}\left[-\log p_{\theta }\left({\mathbf{x}}_0\right)\right]& \le {\mathbb{E}}_q\left[-\log \frac{p_{\theta }\left({\mathbf{x}}_{0:T}\right)}{q\left({\mathbf{x}}_{1:T}\mid {\mathbf{x}}_0\right)}\right]\\ & ={\mathbb{E}}_q\left[-\log p\left({\mathbf{x}}_T\right)-\sum _{t\ge 1}\log \frac{p_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t\right)}{q\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1}\right)}\right]\\ & =-L_{\mathrm{V}\mathrm{L}\cdot \mathrm{B}}\end{array}\text{\hspace{1em}(6)}$$
Ho等人[22]发现，最好不要将${\mu }_{\theta }(x_t,t)$直接参数化为神经网络，而是训练模型${ϵ}_{\theta }(x_t,t)$来预测$ϵ$。因此，通过重新参数化方程（6），他们提出了一个简化的目标，如下所示：
$$L_{\text{simple }}=E_{t,x_0,ϵ}\left[{\Vert ϵ-{ϵ}_{\theta }\left(x_t,t\right)\Vert }^2\right]\text{\hspace{1em}(7)}$$
其中作者将公式（6）中的损失与Song等人[61]中的生成分数网络联系起来。

2.1.2 Noise Conditioned Score Networks (NCSNs)

某些数据分布$p(x)$的得分函数被定义为对数密度相对于输入的梯度$\nabla xlogp(x)$。为了估计这个分数函数，可以训练一个具有分数匹配的共享神经网络。具体来说，分数网络$s_{\theta }$是一个由$\theta$参数化的神经网络，它被训练为近似$p(x)(s_{\theta }(x)\approx \nabla xlogp(x))$，通过最小化以下目标：
$${\mathbb{E}}_{x\sim p(x)}{\Vert s_{\theta }(x)-{\nabla }_x\log p(x)\Vert }_2^2\text{\hspace{1em}(8)}$$
然而，由于计算的计算负担$\nabla xlogp(x)$，分数匹配不可扩展到深度网络和高维数据。为了缓解这一问题，[61]的作者提出利用去噪分数匹配[63]和切片分数匹配[64]。此外，Song等人[61]强调了阻碍基于分数的生成模型在真实数据中天真应用的主要挑战。关键挑战是，由于现实世界中的数据往往集中于嵌入高维空间中的低维流形（流形假设），因此估计的分数函数在低密度区域中是不准确的。作者证明，这些问题可以通过在不同尺度上用高斯噪声扰动数据来解决，因为这使得数据分布更适合基于分数的生成模型。他们建议通过训练单个噪声条件分数网络（NCSN）来估计与所有噪声水平相对应的分数。他们得出$\nabla xlog（p_{{\sigma }_t}(x)$为$\nabla x_{t}log{p}_{{\sigma }_t}(x_t|x)=-\frac{x_t-x}{{\sigma }_t}$，通过选择噪声分布为$p_{{\sigma }_t}(x_t|x)=\mathcal{N}(x_t;x,{\sigma }_t^2,I)$。其中$x_t$是$x$的噪声版本。因此，对于给定的高斯噪声尺度序列，${\sigma }_1<{\sigma }_2<\cdot \cdot \cdot <{\sigma }_T$，方程（8）可以写成：
$$\frac{1}{T}\sum _{t=1}^T\lambda \left({\sigma }_t\right){\mathbb{E}}_{p(x)}{\mathbb{E}}_{x_t\sim p_{{\sigma }_t}\left(x_t\mid x\right)}{\Vert s_{\theta }\left(x_t,{\sigma }_t\right)+\frac{x_t-x}{{\sigma }_t}\Vert }_2^2\text{\hspace{1em}(9)}$$
其中$\lambda ({\sigma }_t)$是加权函数。这一推断是使用一种称为“Langevin动力学”的迭代程序完成的[65，66]。Langevin动力学设计了MCMC程序，仅使用其得分函数从分布$p(x)$中采样$\nabla xlogp(x)$。具体来说，从随机样本$x_0\sim \pi (x)$对来自$p(x)$的样本，它迭代如下：
$$x_i=x_{i-1}+\frac{\gamma }{2}{\nabla }_x\log p(x)+\sqrt{\gamma }\cdot {\omega }_i\text{\hspace{1em}(10)}$$
其中${\omega }_i\sim \mathcal{N}(0,I)$和$I\in \{1,\dots ,N\}$。当$\gamma \to 0$和$N\to \infty$, 从这个过程中获得的$x_i$样本收敛到$p(x)$的样本。[61]的作者提出将该算法命名法修改为退火Langevin动力学算法，因为随着时间的推移，噪声等级${\sigma }_i$逐渐降低（退火），以减轻分数匹配的一些缺陷和失败模式[67]。

2.1.3 Stochastic Differential Equations (SDEs)

与上述两种方法类似，基于分数的生成模型（SGM）[62]将数据分布$q(x_0)$转换为噪声。然而，通过将噪声尺度的数量推广到无穷大，可以将先前的概率模型视为SGM的离散化。我们知道，许多随机过程，如扩散过程，是以下形式的随机微分方程（SDE）的解：
$$\mathrm{d}\mathbf{x}=\mathbf{f}(\mathbf{x},t)\mathrm{d}t+g(t)\mathrm{d}\mathbf{w}\text{\hspace{1em}(11)}$$
其中$f(.,t)$是SDE的漂移系数，$g(t)$是扩散系数，$w$表示标准布朗运动。设$x_0$为未破坏数据样本，$x_T$表示近似标准高斯分布的扰动数据。对于给定的正向SDE，存在反向运行的反向时间SDE，其中，通过从$p_T$的样本开始并反向该扩散SDE，我们可以从数据分布$p_0$中获得样本
$$d\mathbf{x}=\left[\mathbf{f}(\mathbf{x},t)-g^2(t){\nabla }_x\log p_t(x)\right]dt+g(t)d\overline{\mathbf{w}}\text{\hspace{1em}(12)}$$
其中$dt$是无穷小的负时间步长，$w$是向后运行的布朗运动。为了数值求解反向时间SDE，可以通过分数匹配[61，62]训练神经网络来近似实际分数函数，以估计$s_{\theta }(x,t)\approx \nabla xlog{p}_t(x)$（在等式（12）中表示为红色）。该评分模型采用以下目标进行训练：
$$\mathcal{L}(\theta )={\mathbb{E}}_{\mathbf{x}(t)\sim p(\mathbf{x}(t)\mid \mathbf{x}(0)),\mathbf{x}(0)\sim p_{\text{data }}}\left[\frac{\lambda (t)}{2}{\Vert s_{\theta }(\mathbf{x}(t),t)-{\nabla }_{\mathbf{x}(t)}\log p_t(\mathbf{x}(t)\mid \mathbf{x}(0))\Vert }_2^2\right]\text{\hspace{1em}(13)}$$
其中λ是加权函数，$t\sim \mathcal{U}([0,T])$。尤其是$\nabla xlog{p}_t(x)$替换为$\nabla xlog{p}_{0t}(x(t)|x(0))$以规避技术难题。

2.2 临床重要性

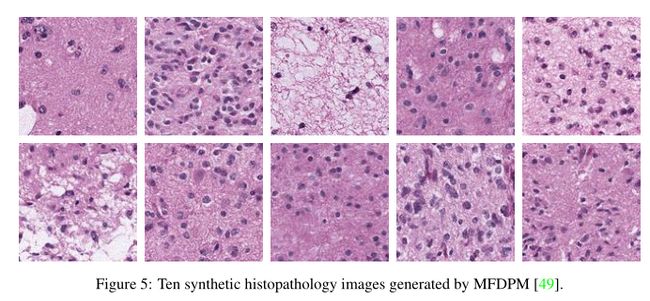
生成模型对医学成像领域产生了重大影响，在医学成像领域，迫切需要工具来改善临床医生和患者的日常生活。具体而言，数据收集程序的复杂性、缺乏专家、隐私问题以及患者授权的强制性要求，在医学成像的注释过程中形成了一个主要瓶颈。这就是生成模型变得有利的地方[68]。几个观点推动了我们对医学成像生成扩散模型的兴趣。在医学领域，由于某些病理的罕见性质，许多数据集遭受严重的类别失衡。扩散模型可以通过生成各种逼真的图像来缓解这种限制，以在医疗领域中发挥作用。此外，生成合成医学图像具有重要的教育价值。扩散模型能够产生不同医学成像模式的独特实例的无限来源，可以通过构建不同的教学和实践合成样本来满足教育需求。此外，这些人工图像可以减轻与公开使用患者数据相关的数据安全问题设置。这些人工图像还可以解决训练用于医学应用的深度神经网络的一个特别显著的困难。通常，医学图像的注释是一个漫长而昂贵的过程，需要专家的帮助。因此，使用扩散模型生成合成样本可以在很大程度上缓解医学数据稀缺的问题。图5描述了使用[49]生成罕见癌症亚型组织病理学图像的案例研究。

3. Diffusion Models in Action

为扩散模型提供分类或多或少遵循与医学成像分析的其他技术相同的路线。然而，我们在图4中为每个子类别的论文提供了详细的附加信息。在本节中，我们探索了基于扩散的方法，这些方法被提出用于解决七个应用类别中的医学图像分析的任何问题，如图4所示：（I）图像到图像转换、（II）图像分割、（III）异常检测、（IV）医学图像重建、，（V）图像生成，（VI）医学图像去噪和（VII）多学科应用，称为其他应用。图4显示了每个类别的大量研究的集合，其中包含关于每个研究的广泛信息，例如研究模式、感兴趣的器官以及研究扩散模型反向过程中使用的特定算法。最后，在第3.8节中，我们讨论了研究中使用的总体算法，并试图阐明表1中论文的主要新颖性和贡献。

3.1 异常检测

医学异常检测是计算机视觉中的一个重要课题，旨在突出图像的异常区域[69，70，71]。近年来，生成模型极大地影响了异常检测的查询，并显示出很有前景的结果。因此，我们将在下一节中探讨扩散模型作为异常检测中的主要生成模型。

Wolleb等人[28]介绍了一种基于去噪扩散隐式模型（DDIM）[72]的弱监督学习方法，用于医学异常检测。给定健康或患病对象的输入图像，首先执行图像到图像的转换，使得目标是将输入图像转换为健康图像。然后，通过从输入中减去输出图像来识别异常区域。该过程开始于通过反向DDIM采样将输入图像编码为噪声图像。然后，通过在健康图像和患病图像上预先训练的二值分类器来引导去噪过程，以产生健康图像。最后，通过获取输出和输入之间的差异来计算异常图。BRA TS2020[73，74，75]和CheXpert[76]数据集的结果表明，与V AE[77]和GAN[78]模型相比，所提出的方法具有优势。

Wyatt等人[53]在AnoDDPM中仅在健康医学样本上训练DDPM。然后通过计算输出图像和输入图像之间的差异来渲染异常图像。他们还表明，在高斯噪声上利用单纯形噪声显著提高了性能。

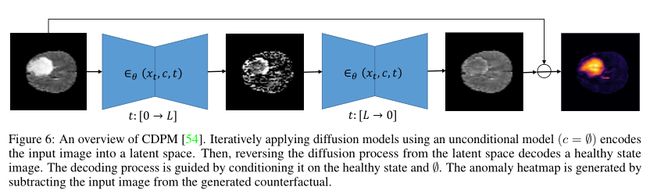
相反，CDPM[54]证明，仅在健康数据上训练扩散概率模型会产生较差的分割性能。因此，CDPM提出了一个反事实扩散概率模型，用于从实际输入图像生成健康的反事实。如图6所示，通过使用无条件模型迭代应用扩散模型，输入图像最初被编码到潜在空间中。然后，通过反转扩散过程来完成解码步骤。使用隐式指导[79]，通过将其调节为健康状态，将潜势解码为反事实∅. 受到[80，81，82]的启发，桑切斯等人[54]然后通过将条件注意纳入U-Net主干来增强条件调节过程。作为最后一步，在推断期间应用动态归一化技术，以避免潜在空间像素中的饱和，这是由可能改变图像统计的引导迭代过程引起的。最后，通过从生成的健康反事实中减去输入图像来确定异常的位置。

3.2 去噪

医学成像的主要挑战是在不丢失重要信息的情况下获得图像。在采集和/或进一步处理阶段期间，获得的图像可能被噪声或伪影破坏[83，84]。噪声会降低图像质量，当成像对象较小且对比度相对较低时，噪声尤其显著[85]。由于生成模型的性质，扩散模型便于处理各种去噪问题。在本节中，我们将探讨扩散模型对该领域的贡献。

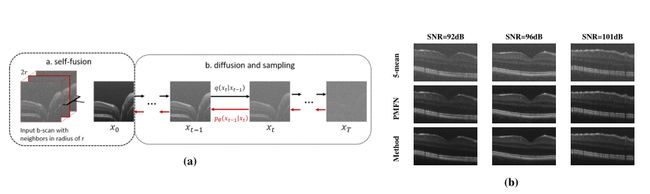
Hu等人[47]使用DDPM[22]以无监督的方式对光学相干断层扫描（OCT）体积视网膜数据进行去斑，表示为DenoOCT DDPM。OCT成像实用程序受到空间频率带宽的限制，这导致生成的图像包含斑点噪声。斑点噪声阻碍眼科医生的诊断，并会严重影响组织的可见性。经典的方法，如在同一位置对多个b扫描进行平均，具有极大的缺点，如采集时间长和配准伪影。由于散斑噪声的乘法特性，这些方法丰富而不是减少噪声。基于深度的模型表现出色。然而，这种性能取决于无噪声图像的可用性，这是一种罕见且成本高昂的获取过程。为此，DenoOCT DDPM[47]利用DDPM在噪声模式而非真实数据模式中的可行性。因此，他们使用自融合[86]作为预处理步骤，为DDPM提供清晰的参考图像，并训练参数化马尔可夫链（见图7a）。他们的研究证明了伪模态融合网络（PMFN）[87]上的SOTA结果，该网络使用了来自单帧噪声b-scan的信息，以及借助于自融合[86]方法创建的伪模态，关于信噪比（SNR）度量。图7b所示PMNF的定性结果（以多个采集SNR表示）证实了扩散模型在去除斑点噪声的同时保留小血管等细粒度特征的能力。

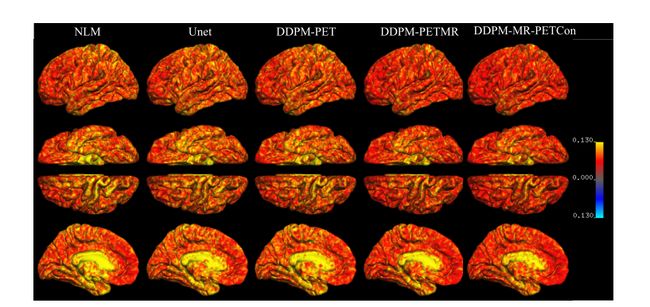
正电子发射断层扫描（PET）是一种非侵入性成像工具，在癌症筛查和诊断中发挥着至关重要的作用。然而，与OCT设备一样，PET由于对患者的低束计数辐射而具有低SNR和分辨率。PET图像去噪的深度学习方法已经取得了进步，但过度平滑是基于CNN的方法的一个突出缺点。因此，条件生成对抗网络（CGAN）[88，89]抵消了上述缺陷，但仍依赖于训练和测试集分布。Gong等人[46]提出了基于DDPM的PET去噪框架，并将辅助模态嵌入作为DDPM公式的先验信息，即PET-DDPM。Gong等人分别使用18F-FDG和18F-MK-6240数据集进行PET和MR检查。PET-DDM是一项多学科研究，研究通过PET图像学习噪声分布的过度协作模式。这种直觉遵循原始论文中的生成范式[23]，通过引导分类器将学习到的分布收敛到期望的分布。与基于U-Net[90]的去噪网络相比，PET-DDM在峰值信噪比（PSNR）和结构相似性指数度量（SSIM）方面产生了SOTA结果。

3.3 重建

计算机断层扫描（CT）和核磁共振成像（MRI）等医学成像方式是医学中最流行的成像工具。然而，由于其功能性，它们可能会伤害患者；因此，它们的辐射暴露从标准剂量减少，或者成像过程以欠采样或稀疏视图的方式进行[91，92，93，94]。为了减少这些缺点，例如低信噪比（SNR）和对比度噪声比（CNR），医学图像重建必须克服上述挑战，并解决这个不适定反演问题[95]。

本节概述了基于扩散的医学图像重建和增强范例。

磁共振成像（MRI）是医学诊断治疗中一种流行的非侵入性成像工具，但由于其固有的物理特性，它是一个耗时的成像过程，其中患者的运动会导致图像中的各种伪影。因此，为了减少就寝时间并加速从空间域（或k空间）到图像级别的反向问题解决，在监督学习概念中提供了各种解决方案。然而，这些方法对其训练/测试集中的分布变化或漂移并不鲁棒。Jalal等人[96]提出了通过生成模型压缩传感（CSGM）在MRI重建领域的第一项研究。为此，CSGM在MRI图像上训练基于分数的生成模型[67]，以利用Langevin动力学[97]作为反演路径的先验信息，从后验采样方案中的欠采样MRI重建真实的MRI数据。与端到端监督学习范式相比，CSGM[96]通过结构相似性指数度量（SSIM）和PSNR度量证明了其优于fastMRI[98]和斯坦福MRI[99]数据集的性能。

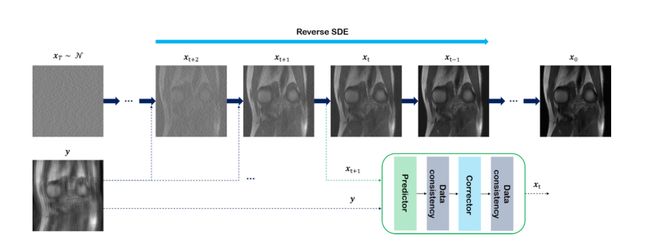
Cheng等人[37]提出了一种基于分数的扩散框架，该框架解决了加速MRI扫描图像重建的逆问题，如图9所示。在第一步中，具有去噪分数匹配的单个连续时间相关分数函数仅使用幅度图像进行训练。然后，在反向SDE过程中，利用方差分解（VE）-SDE[62]从预训练的得分模型分布中采样，条件是测量。

然后，在每个步骤中，首先将图像分割成实分量和虚分量。每个部分都被输入预测器，然后进行数据一致性映射以重建图像。再次分割所获得的图像，并将校正器和数据一致性映射应用于每个部分，以分别补偿扩散期间的误差和重建改进的图像。结果表明，所提出的模型优于先前的SOTA方法[100，101，98]，甚至可以重建数据，该数据在训练分布之外相当高的保真度，例如重建训练过程中看不到的解剖结构。此外，当存在多个线圈时，所提出的框架对于重建图像非常有效。对于上述问题，他们提出了两种方法：（1）并行重建每个线圈图像；（2） 它们通过在反向SDE期间的每个给定步骤处注入线圈图像之间的相关性来考虑线圈图像间的相关性。然后，通过获取每个重建线圈图像的平方根和（SSoS）[102]来获取最终图像。尽管这两种技术在质量和实践上都显示出了很好的效果，但它们很耗时。

3.4 分割

图像分割是计算机视觉中的一项重要任务，它通过将图像分解为多个有意义的图像片段来研究简化图像的复杂性[103104]。具体来说，它通过提供有关解剖相关区域的有益信息来促进医学分析。然而，深度学习模型通常需要大量不同的像素注释训练数据，以产生可推广的结果[105106]。尽管如此，由于所需的时间、成本和专业知识，可用于医学图像分割的图像和标签的数量受到限制[107108109]。为此，通过合成标记数据并消除像素注释数据的必要性，扩散模型已被推进到图像分割研究的前沿。

brainSPADE[43]提出了一种用于合成标记的脑部MRI图像的生成模型，该模型可用于训练分割模型。brainSPADE由标签生成器和图像生成器子模型组成。前者负责创建合成分割图，后者负责基于生成的标签合成图像。在标签生成器中，首先在训练期间使用空间VAE编码器对输入分割图进行编码，并构建潜在空间。然后，压缩的潜在代码通过LDM[82]进行扩散和去噪，并产生一个有效的潜在空间，其中忽略了不可察觉的细节，并更加突出了语义信息。然后，空间V AE解码器经由潜在空间构建人工分割图。在图像生成器中，Fernandez等人[43]利用SPADE[110]（一种V AE-GAN模型），从输入的任意风格构建风格潜在空间，并将其与人工分割图一起用于解码输出图像。nnU Net[111]被用于检查性能。研究结果表明，当在合成数据上训练时，与在实际数据上训练的结果相比，该模型获得了可比较的结果，并且它们的组合显著改善了模型结果。

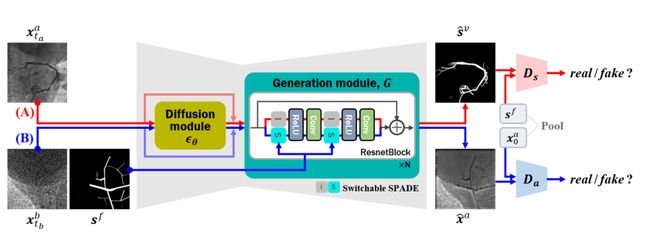
Kim等人[44]提出了一种用于自我监督血管分割的新型扩散对抗性表示学习（DARL）模型，旨在诊断血管疾病。所提出的DARL模型有两个主要模块：一个扩散模块，用于学习背景图像分布，另一个生成模块，用于使用可切换的SPADE算法生成血管分割掩模或合成血管造影[110]。图10说明了应用该方法的两种方式。在路径（A）中，真实的噪声血管造影图像xata被输入到模型中以产生分割掩模ûsv，并且SPADE开关被关闭。在路径（B）中，真正的噪声背景图像xbtb被输入到该模型中，SPADE变为活动的并接收血管状分形掩模，从而生成合成血管造影图像ûxa。然后，通过将生成的合成血管造影图像提供给路径（A），形成循环，这有助于学习血管信息。

此外，在推断期间，在一个步骤中执行路径（A），其中模型通过仅将有噪声的血管造影图像输入到模型中来产生掩模。结果验证了与SOTA无/自监督学习方法相比，所提出方法的泛化性、鲁棒性和优越性。

3.5 图像翻译

获取用于诊断和治疗的多模态图像通常是至关重要的。此外，在某些情况下，我们可能会错过模式。扩散模型显示了利用交叉模态生成缺失模态和利用其他模态类型生成模态的有利结果，例如从MRI转换为CT。

CT和MRI是最常见的两种成像类型。然而，CT在显示复杂的软组织损伤图像方面受到限制。因此，在收到初始CT结果后，可能需要进行后续MRI以进行最终诊断。然而，除了耗时和昂贵之外，该过程还可能导致MRI和CT图像之间的错位。为此，Lyu等人[32]利用最近引入的DDPM[112，22]和基于分数的扩散模型[62]来解决两种模式之间的转换问题，即从MRI到CT。特别是，他们提出了条件DDPM和条件SDE，其中，他们的反向过程以T2w MRI图像为条件，并进行了全面的实验。作者采用了三种不同采样方法的DDPM和SDE，并将其与现有的基于GAN的[113]和基于CNN的[90]方法进行了比较。这三种方法旨在求解逆时间SDE方程（12），可总结如下：

​ 1. Euler Maruyama（EM）方法：使用简单的离散化技术，其中dt替换为∆t和具有高斯噪声$z\sim \mathcal{N}(0,∆t\cdot I)$的$dw$，方程（12）可以求解。

​ 2. 预测-校正（PC）方法：在这种方法中，预测和校正过程发生在嵌套循环中，在该循环中，先预测先前的数据，然后分几个步骤进行校正。可以使用EM来求解预测值。由于校正器可以是任何基于分数的马尔可夫链蒙特卡罗（MCMC）方法，包括退火Langevin动力学，因此可以使用方程（10）中的Langevin动态来求解。

​ 3. 概率流ODE方法：方程（11）中的SDE方程可以写成如下ODE方程：
$$d\mathbf{x}=\left[\mathbf{f}(\mathbf{x},t)-\frac{1}{2}{g}^2(t){\nabla }_x\log p_t(x)\right]dt\text{\hspace{1em}(14)}$$

​ 因此，通过解决ODE问题，可以找到$x_0$。然而，尽管ODE是一个快速求解器，但它缺少一个纠正错误的随机项，导致性能略有下降。

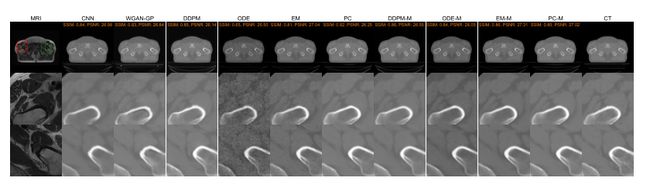
他们在Gold Atlas男性骨盆数据集[114]上的广泛实验表明，在SSIM和PNSR方面，扩散模型优于基于CNN和GAN的方法。此外，他们使用蒙特卡罗（MC）方法来研究扩散模型的不确定性；在这种技术中，模型输出十次，平均值得出最终结果。定性结果如图11所示。

为了解决缺失模态问题，Meng等人[33]提出了一种统一的基于多模态条件分数的生成方法（UMM-CSGM），该方法基于所有剩余模态作为条件来合成缺失模态。所提出的模型是SDE[62]的条件格式，其中它仅使用基于分数的网络来学习不同的跨模态条件分布。对BraTS19数据集[73，74，75]的实验表明，与SOTA方法相比，UMM-CSGM能够生成具有更高保真度和脑组织结构信息的缺失模态图像[115，116，117，118，119]，该数据集包含每个受试者的四种MRI模态。

3.6 图像生成

图像生成是扩散模型的主要目标之一，已广泛应用于各种风格，包括生成合成2D/3D医学图像[48，49，51，52]，从2D细胞图像重建3D细胞[50]等。本节将概述基于扩散的医学图像生成方法。

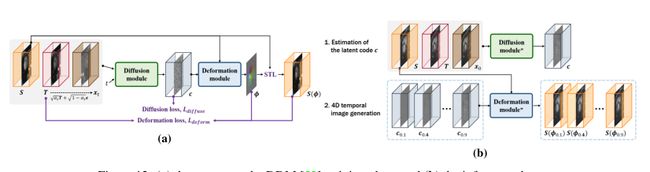
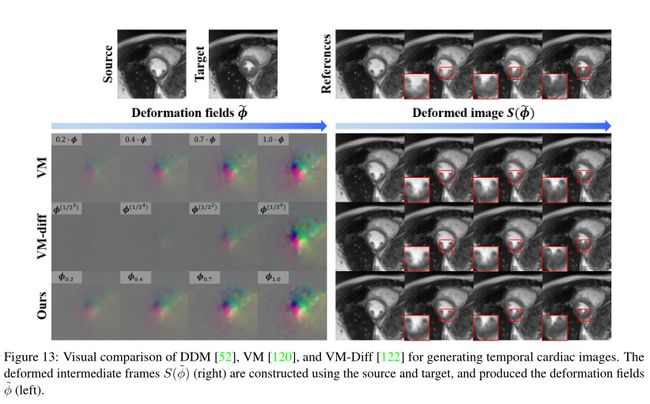
使用4D成像跟踪解剖变化是医学中跟踪3D体积随时间变化以检测异常和疾病进展的方法之一。这种4D图像主要通过MRI获得，但这是一个相对耗时的过程。Kim等人[52]最近提出了扩散可变形模型（DDM），该模型获取源图像和目标图像，并沿连续轨迹生成中间时间帧。该方法包括两个主要模块：（i）去噪扩散概率模型（DDPM）模块和（ii）变形模块。在DDPM模块中，通过学习源图像和目标图像来构造潜代码，并且在变形模块中，使用获取的潜代码和源图像来渲染变形图像。在训练阶段，如图12a所示，从[22]导出的扩散模型获取源、目标和扰动目标图像，并输出潜码。沿着源图像学习的潜代码被馈送到变形模块，从[120]中采用，并创建变形场。然后，使用具有三线性插值的空间变换层（STL）[121]，使用变形场扭曲源体积，以构建变形的源图像。然后，推断开始于扩散模块提供潜码，潜码包含从源到目标的空间信息（见图12b）。然后，使用变形模块通过用因子缩放潜码来生成变形的中间帧，该因子是[0，1]的元素。

组织病理学涉及微观层面的组织和细胞研究，以诊断疾病和癌症[123]。然而，组织学图像对于某些癌症亚型来说是罕见的，从而增加了生成模型填补空白的意义。为此，Moghadam等人[49]首次研究采用DDPM生成组织病理学图像。具体来说，他们利用基因型指导的DDPM合成包含各种形态学和基因组信息的图像。为了解决这个数据一致性问题，并强制模型更加关注形态模式，他们首先将输入图像馈送到颜色归一化模块[124]，以统一所有图像的域。此外，他们应用形态学级别优先化模块[125]，该模块为早期级别的损失指定更高的权重值，以强调感知信息，并为后期级别的损失提供更低的权重，从而导致保真度样本。在癌症基因组图谱（TCGA）数据集[126]上的实验表明，与基于GAN的方法相比，所提出的方法具有优势[127]。

3.7 其他应用和多任务

根据图4，仍有一些研究无法被分配到特定类别，扩散的使用不限于这六个类别。多尺度DDAM[56]利用DDPM[22]设计高斯噪声对抗性攻击的中和概念。扩散模型并不局限于医学领域中与视觉相关的任务，它可以是生物学中的一项创新。[57128]中提出的平台可用于设计药物和疫苗。在下面的段落中，我们探讨了最近在多任务学习中使用的一些基于扩散的方法以及在医学领域中的独特用途。

无监督/自监督学习是医学图像去噪的理想替代方法，其中访问成对的干净和有噪声的图像很难实现[129，130]。传统的基于深度的网络利用最小均方误差（MMSE）估计，这导致由于训练/测试数据的分布变化或高斯噪声的初步假设与数据的实际分布不一致而导致图像不令人满意和模糊。Chung等人[58]提出了一种用于MRI图像去噪和超分辨率的多连续范式，即R2D2+，使用SDE[62]算法来解决上述缺陷。扩散生成模型对数据上的任何分布变化都是鲁棒的，并产生更真实的数据[23]。尽管扩散模型具有优势，但它们非常耗时。为此，Chung等人[58]不从纯噪声开始反向扩散过程，而是从初始噪声图像开始。

R2D2+[58]使用基于协方差矩阵特征值分析的非参数估计方法而非传统的数值方法[62]解决了反向时间SDE过程。为了通过该过程抑制结构减缓，R2D2+使用低频正则化来阻止图像的低频对应物中的任何变化。R2D2+在去噪步骤之后将相同的网络用于超分辨率任务。单线圈快速MRI[98]膝关节数据集和私人肝脏MRI数据集的总体结果表明，在SNR和对比噪声比（CNR）度量方面，该方法优于传统SOTA非/自监督学习方案。

Pinaya等人[59]提出了一种基于DDPM的快速方法，用于检测和分割脑部MR图像中的异常区域（见图14）。该方法遵循生成健康样本并通过从输入图像中减去异常分割图来描绘异常分割图的策略。为此，在[82]之后首先采用VQ-V AE[131]，其将输入图像编码为紧凑的潜在表示，并利用码本从输入图像提供量化的潜在表示。然后，DDPM使用所获取的潜在空间并学习健康样本的潜在表示的分布。通过应用在反向过程的中间样本的平均值上预先计算阈值，其包含更少的噪声和更明显的值。使用中间步骤作为反向处理的起点，他们对图像的异常区域进行去噪，并使用获得的掩模保留其余区域，从而从样本中去除病变。最终，在解码样本时，产生健康图像。

3.8 比较概述

表1根据直接使用或启发的算法对已审查的扩散模型论文进行了全面分类：（1）DDPM，（2）NCSN，和（3）SDE。此外，表1强调了每种算法的关键概念和目标，并代表了可根据已审查论文在未来研究中调查和利用的实际用例。

显然，调节反向扩散过程是获得期望输出的最受研究的方法之一。该引导过程可以使用不同的约束类型来完成。在[32，36，50]中，他们通过使用图像应用条件来控制反向过程；特别是，Lyu等人[32]利用T2w MR图像调节DDPM和SDE以获得CT图像，Xie等人[36]提出了用于欠采样医学图像重建的测量调节DDPM，Waibel等人[50]使用2D显微图像约束3D模型以生成3D单细胞形状。此外，BrainGen[39]制作了真实的脑部扫描示例，这些扫描基于年龄、性别、心室容积和相对于颅内容积的脑容积等元数据。此外，[28]和[54]中分类器和隐式指导方法的使用已经得到了彻底的研究。通过这种方式，分配以更可能达到预期结果的方式进行转移。

扩散模型的一些主要问题和局限性是其速度慢和所需的计算成本。

已经开发了几种方法来解决这些缺点。无训练去噪扩散隐式模型（DDIM）[72]是旨在加速采样过程的进步之一。DDIM通过用非马尔可夫过程代替马尔可夫过程来扩展DDPM，从而导致更快的采样过程，且质量下降可忽略不计。[132133]提出了适当的初始化，而不是反向过程中的随机高斯噪声，从而导致显著的加速。具体而言，Chung等人[133]证明，基于随机收缩理论，例如，在预训练神经网络的一步预测之后，开始回归，加快了反向扩散并减少了反向采样的次数。Dar等人[39]还验证了对抗性学习可以将反向扩散速度提高两个数量级。

还研究了几种方法来提高扩散模型的输出质量。AnoDDPM[53]证实，推广到其他类型的噪声分布可以提高任务特定的质量。他们确定，在异常检测的情况下，单纯形噪声显示出优于高斯噪声的优势。此外，Cao等人[132]证实，仅在图像的高频部分操作扩散过程可提高MRI重建的稳定性和质量。

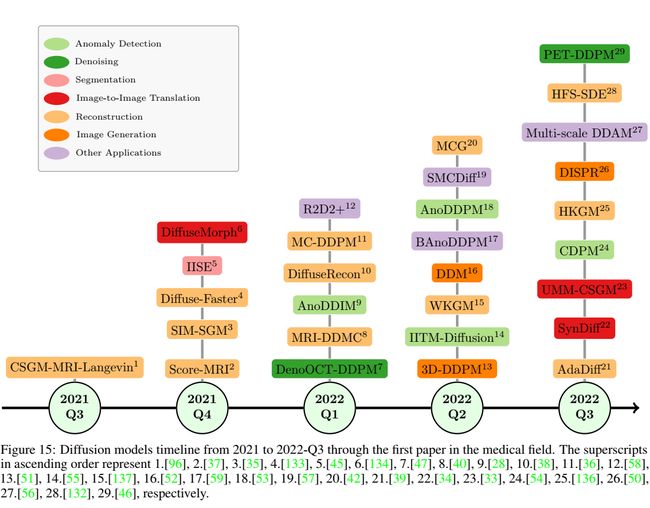
由于其显著的结果，扩散模型已经证明，它们可以成为其他生成模型的有力竞争对手，如图15所示，这一领域在学术环境中前景广阔。

4. 未来方向和开放挑战

扩散模型正在成为医学视觉和医学生物学领域的热门话题；证据显示，图3中的趋势呈上升趋势。由于该领域缺乏此类数据，扩散过程不需要一对标记或未标记的数据，这使其成为医学图像分析的有力候选。本文收集了最新的医学相关论文，并根据图4中提出的分类法对其中许多进行了调查，以证明扩散模型的威力。我们希望这篇综述能够揭示医学领域中扩散模型的出现，并为读者提供指导。

因此，在本节中，我们强调了未来调查的开放方向。此外，由于扩散模型的性质，它们是多种模态医学图像去噪的有力候选。尽管如此，有限数量的研究解决了这一问题（见第3.2节），使其适合进一步研究。为了澄清这一点，超声波使用高频来观察身体内部，因此当穿透组织时，透射的超声波束会减弱。此外，射频（RF）数据包含由采集卡和传感器噪声带来的附加高斯噪声[139]。因此，扩散模型可以弥补超声成像技术的缺陷实际上不是使用传统方法，例如，增加由安全阈值控制的发射波束的功率，平均连续帧以阻止导致低帧速率的噪声效应，并降低降低空间分辨率的发射频率。

扩散模型通常存在缺陷，可能会转移到早期医学研究中。首先，扩散模型是一个耗时的过程，源于在推断时间执行迭代步骤以生成样本。第二，大多数工作关注通过扩散模型的高斯噪声分布，忽略了其他扰动，例如泊松噪声，这是PET等成像模态中最可能的分布[140]。

促进上述限制的努力可能是医学领域利用扩散模型的研究方向。

由于医学成像中的隐私问题限制了数据集成，扩散模型和联合学习可以在医学领域创建一个深刻而强大的学习平台。此外，由于同样的隐私问题，扩散模型可以整合其生成用于教育目的的合成医学数据的步骤。扩散模型的逆问题求解可以通过强化学习范式来执行，以估计最佳反演路径，而不是可靠的数学解。扩散模型成为文本到图像任务的基石[80，141]。然而，相反的问题，图像到文本，仍处于早期阶段[142]，这是一个很有希望的研究方向，以产生综合文本，如医学图像的转录本，作为医生的辅助信息。

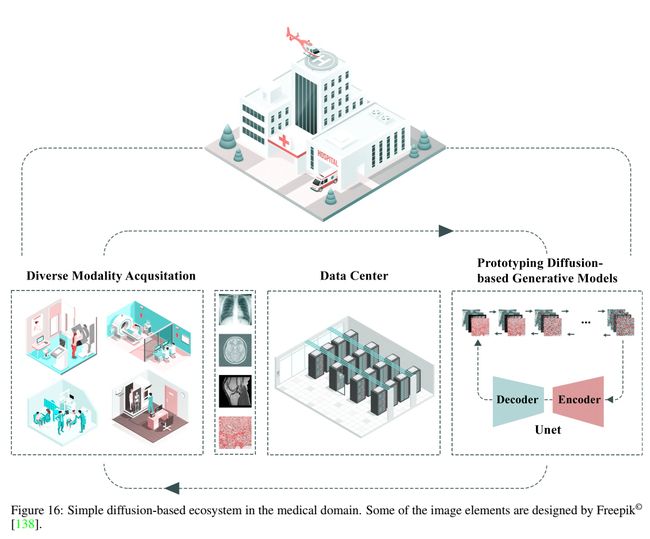
利用条件扩散模型在MRI和PET分析中使用CT图像等元数据可能是医学领域扩散研究的另一个偏差。最后，由于扩散模型在各种医疗任务中的广泛使用（正如我们在本次调查中所研究的那样），创建包含这些任务的扩散模型的软件生态系统将非常重要，类似于原始研究，如nnU Net[111]和Ivadomed[143]。在图16中，我们描述了特定医疗机构（即医院）内小规模的简单提案生态系统。该管道的第一步是从组织中不同成像系统内的数据采集开始。然后，通过应用预处理步骤，将数据存储在数据中心中，以便与基于扩散的软件共享以达到预期目的。

5. 结论

在本文中，我们对扩散模型的文献进行了综述，重点是在医学成像领域的应用。具体而言，我们研究了漫射器在异常检测、医学图像分割、去噪、分类、重建、合成、生成和其他任务中的应用。特别是，对于这些应用程序中的每一个，我们从各个角度提供了核心技术的分类和高级抽象。此外，我们基于技术对现有模型进行了表征，其中我们确定了基于DDPM、NCSN和SDE的三种主要扩散建模公式。最后，我们概述了未来研究的可能途径。