西瓜书第三章——线性模型

---

前言

我们已经知道，通过机器学习获得的模型就是一种“规律”，它反映了输入和输出之间的关系（如线性的、非线性的）。接下来要讲的线性模型，就是将输入、输出的关系假设为线性的，可以将此线性模型理解为一条直线。因为不可能所有的样本点都落在我们假设的模型上，所以会有误差；这里使用“均方误差”作为标准，并使用最小二乘法或极大似然估计法求出均方误差最小的模型。当然，肯定也存在非线性关系的 x 和 y 得情况，这时候引入广义的线性模型来解决。

---

一、一元线性回归

0、一些基本概念

-序关系
我们要使用线性的规律（即线性公式）作为一个预测的模型，则输入 x，输出 y都得以数的形式表示（而且是连续的），这时需要离散数据连续化。假设 x 此时只包含一种属性，那么它的取值可能是离散的：
1、例如“高度”，取值有“高”、“中”、“低”，因为高度肯定是有大小的，所以这里的“高度”属性就具有序关系，我们在进行离散数据连续化的操作时，就要按照序关系将连续值分大小。
2、如果是“瓜类”，取值有“冬瓜”、“南瓜”、“西瓜”等，这里因为“瓜类”不分大小，所以此属性无序关系。

1、算法原理

线性回归试图学得：f(xi) = ω*xi+b，使得 f(xi) ≅ yi。这里 xi 只包含一个属性，所以为“一元线性回归”。

2、线性回归的最小二乘估计和极大似然估计

2.1、最小二乘法

为了衡量 f(x)与y之间的差别，使用“均方误差”来作为性能指标（回归任务中最常用）。

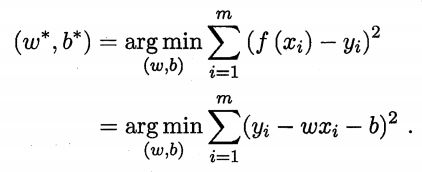
基于上述公式，均方误差最小化来进行模型求解的方法称为最小二乘法。最小二乘法就是试图找一条直线，是所有样本到直线上的欧氏距离之和最小。

2.2、极大似然估计法

极大似然估计思想：在只有概率的情况下，忽略低概率事件直接将高概率事件认为是真实事件。
这里假设此线性回归的模型：y = ωx + b + ε 。ε为不受控制的随机误差，通常假设其服从正态分布 ε ~ N（0，σ^2）（高斯提出，可由中心极限定理解释）。则 p（ε）为：

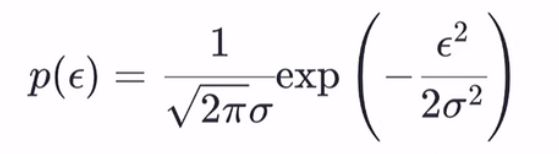
将 ε 用 y - （ωx + b）等价替换可得

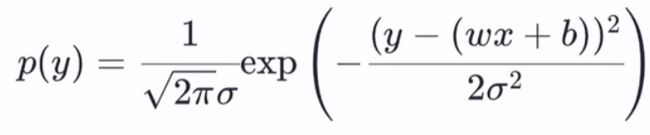
此时 y 服从N（ω*x + b ，σ^2），假设有m个样本（xi，yi）。则似然函数：


最大化上述似然函数，即等价于最小化“均方误差”：

因此 可以总结出：极大似然估计等价于最小二乘法。

3、求解ω和b

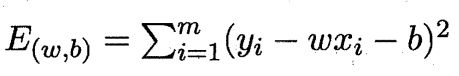
求解ω和b使得上述 平方损失（即均方误差）最小的过程，称为 线性回归模型的最小二乘“参数估计”。

简单地说，上述函数为凸函数。根据凸函数性质，对该函数的两个变量ω和b分别求偏导，令两偏导数为0，求得的ω和b即为最终解。

3.1、凸函数

定义：若在区间 [a，b] 上，函数 f 在此区间上的两点 x1、x2，满足 f( (x1 + x2) / 2 ) <= ( f(x1) + f(x2) ) / 2，则称 f 为区间 [a，b] 上的凸函数。
一个证明函数是否为凸函数的方法：海塞矩阵的半正定性。
这里有引入了海塞矩阵和半正定性的概念。

3.2、海塞矩阵及其半正定性

海塞矩阵定义：设函数 f ，自变量 x= {x1，x2，，，，xn}T，f 对每个自变量 xi 都存在二阶偏导数，则称 f 在 x 处二阶可导。此时有海塞矩阵：

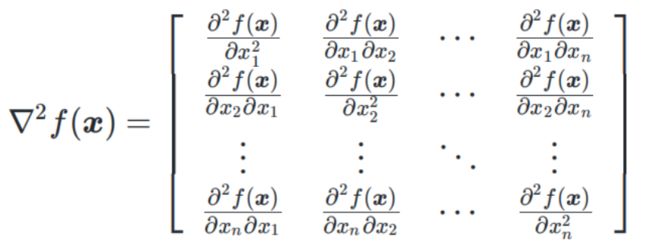
了解什么是海塞矩阵后，还需要知道一个证明海塞矩阵半正定性的方法。

实对称矩阵的所有顺序主子式均为非负，则该矩阵为半正定矩阵。

3.3、海塞矩阵的半正定性证明

首先将我们的平方损失函数E（ω，b）在（ω，b）上的海塞矩阵计算出来：

即分别求ω，b对应的二阶偏导，以及混合偏导。得到海塞矩阵结果：

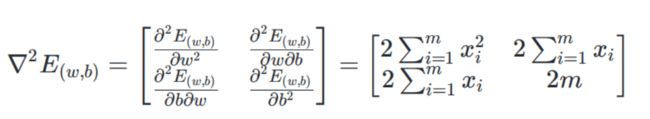
然后通过计算顺序主子式：

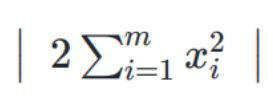
这里不再计算，最终得到的主子式结果都大于0，所以该平方损失函数E（ω，b）为凸函数。
这样就可以对E（ω，b）使用凸函数的性质：让函数对（ω，b）分别求偏导并等于0，求得最佳的（ω*，b*）：

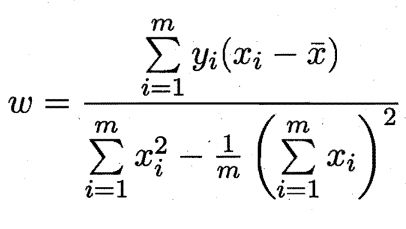
3.4、向量化成矩阵简化python编写

上式得到的ω可以通过一些技巧化简成矩阵的形式：

4、机器学习三要素

• 模型：根据具体问题，确定假设空间。（是线性的假设空间、还是非线性的假设空间）
• 策略：根据评价标准，确定选取最优模型的策略（通常会产出一个“损失函数”)。
• 算法：求解损失函数，确定最优模型。

二、多元线性回归

1、多元线性模型

更一般的情形是：假设数据集D，样本由 d 个属性描述。此时我们试图学得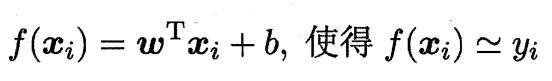
这称为“多元线性回归”。

2、最小二乘法估计以及向量化

首先将模型化为矩阵形式：令 ω ̂ = (ω ; b) ，xi ̂ = (xi ; 1) 。这里将 b 也作为一个“已确定的属性”放入 ω ̂中，对应的 xi 在此属性上的值为 1。那么原公式可表示为
由最小二乘法可得损失函数

再将此损失函数向量化


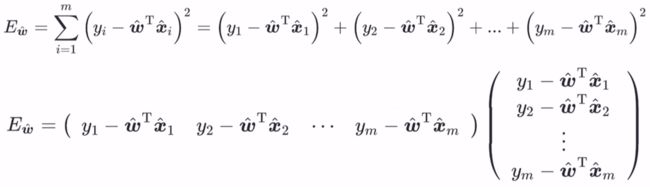
最后得到：

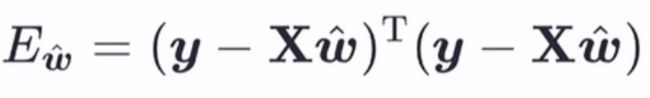
3、求解ω ̂ 和矩阵求偏导的一些公式

求解ω ̂ 仍然使用凸函数的方法，证明其为凸函数——>再利用凸函数的性质求ω ̂。

3.1、海塞矩阵的正定性

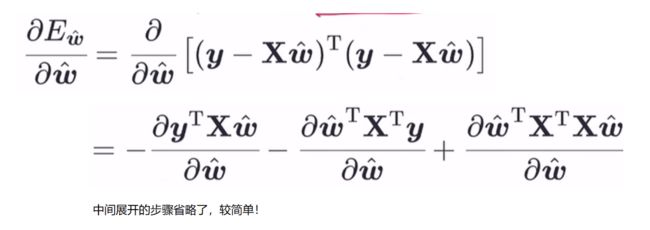
上述对ω ̂求偏导，即对向量求偏导，且函数也是矩阵的形式，我们可能没有学过相关的知识。先了解一些矩阵求导，后面直接代公式即可。

3.2、矩阵求偏导简单了解及相关公式

公式一：

公式二：

由公式一、二可将 3.1节的偏导数化简：

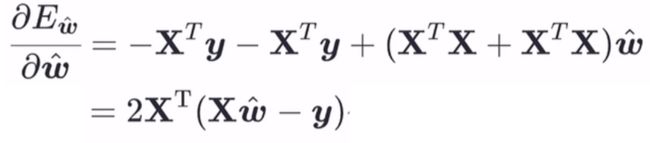
因为此损失函数对ω ̂的海塞矩阵为二阶偏导数，所以继续在上式基础上求偏导：

这里，不能保证此结果必然为正定矩阵，所以西瓜书里假设其为正定矩阵。我们就将按照西瓜书来，那么此损失函数就是凸函数了。利用凸函数的性质求解ω ̂：

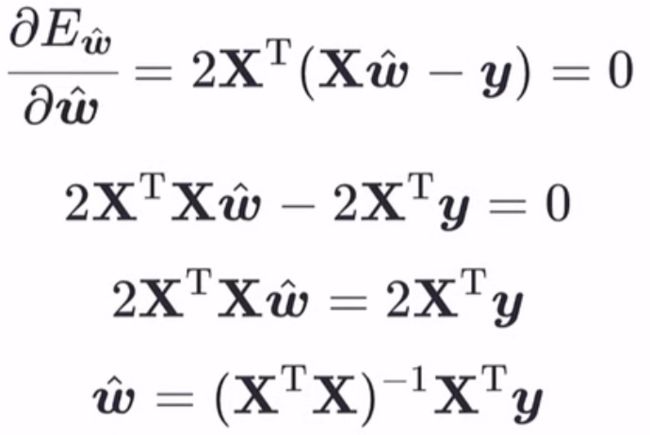
三、对数几率回归

我们知道，按照预测的值是连续的还是离散的，可将学习任务分别分为回归、分类。这里，对数几率回归虽然是“回归”，但实际是一个分类任务。

1、算法原理

在线性模型的基础上套一个映射函数来实现分类功能。因为线性回归得到的值域∈R，而分类的值域要∈（0，1），映射函数的目的就是将R这个值域变换到（0，1）上，这里所使用的映射函数为


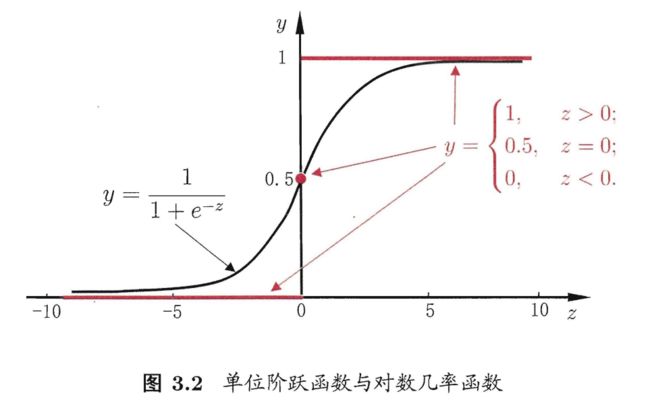
变换之后，将 z = ω*x + b 代入到对数几率函数中（这里 z 是线性回归函数），得到

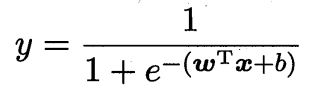
2、极大似然估计角度推导损失函数

将上式的 y 看作 y=1 （预测为正）的概率的话，即后验概率

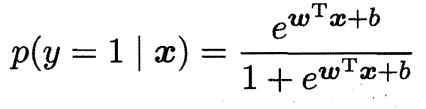
那么，y = 0（预测为负）的概率为

同线性回归时对多元属性的简化处理，这里同样将 ωT*x + b 简化，得到

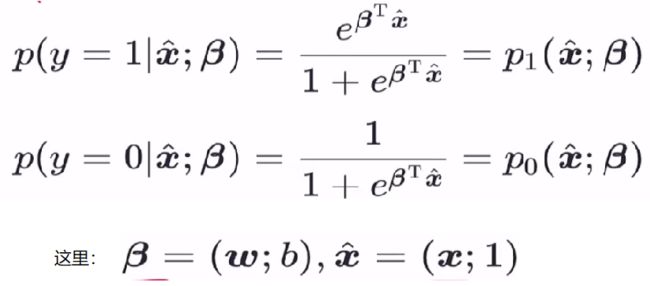
关于随机变量 y∈（0，1）的概率质量函数为：

极大似然估计（中间简化过程省略了）：

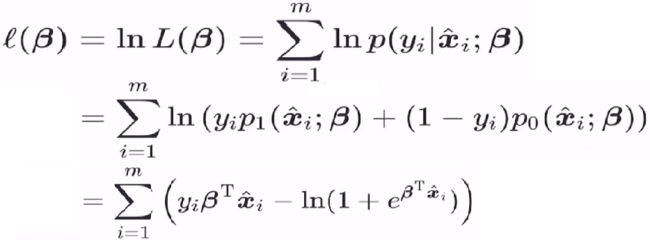
由于损失函数通常是以最小化为优化目标，因此这里取 极大似然函数的负数 为损失函数。

3、信息论角度推导损失函数

3.1、信息熵

定义：度量随机变量X的不确定性，信息熵越大越不确定。这里以离散随机变量为例：

3.2、相对熵（KL散度）

定义︰度量两个分布的差异，其典型使用场景是用来度量理想分布 p(x) 和模拟分布 q(x) 之间的差异。

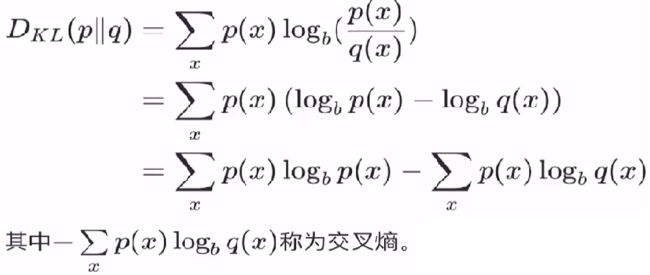
3.3、最小化相对熵得到最优分布的策略

从机器学习三要素中 策略 的角度来说，与理想分布最接近的模拟分布即为最优分布，因此可以通过最小化相对熵这个策略来求出最优分布。由于理想分布p(x)是未知但固定的分布（频率学派的角度)，所以相对熵的前一部分为常量，那么最小化相对嫡就等价于最小化交叉嫡：

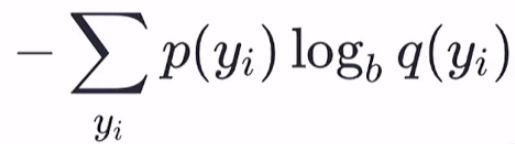
以对数几率回归为例，对单个样本 yi 来说，它的理想分布是：

它的模拟分布为：

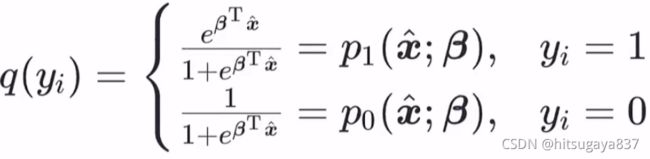
将理想分布、模拟分布代入到交叉熵公式中，化简得到：

那么全体训练样本的交叉熵为：

化简后得到：

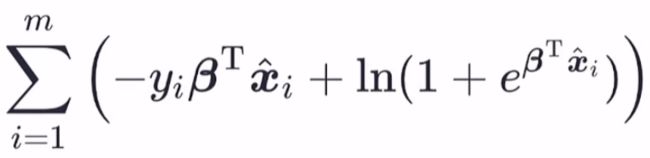
殊途同归，从信息论角度得到的损失函数与极大似然函数所得到的损失函数表达式一样~

4、对数几率回归算法的机器学习三要素

• 模型
  线性模型，输出值的范围为[0,1]，近似阶跃的单调可微函数
• 策略
  极大似然估计，信息论（得到损失函数）
• 算法
  梯度下降，牛顿法（因为无法准确计算出ω的值，这些方法只能得到近似值）

四、二分类线性判别分析

1、算法原理（模型）

线性判别分析（LDA）的思想：给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近、 异类样例的投影点尽可能远离。

这里假设数据集D，包含 m 个样本（xi，yi），xi∈R^n（及每个样本包含 n 个属性），yi∈{0，1}。Xi表示属于同一类的样本集合（0类或1类），μi表示同一类样本的均值向量，∑i 表示第 i 类样本集合对应的协方差矩阵。

2、损失函数推导（策略）

我们要考虑两个方面：异类样本尽可能离得远，同类样本尽可能离得近。
1、首先对于异类样本，这里考虑样本均值向量 μi。二分类时，μ0 和 μ1 在 ω 上的投影分别为： μ0 * cosθ0、μ0 * cosθ1（θ0、θ1分别为两个均值向量与 ω 的夹角）。两个投影值的差要尽可能的大，即得到公式：

这里投影值都扩大了ω 倍，只是为了简化公式（以内积的形式存在，不用 θ 角），简化后为：

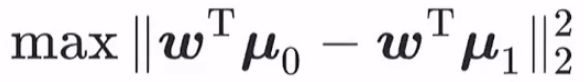
2、对于同类样本，方差尽可能要小。即每个同类样本的投影与它们的均值向量的投影的差越小越好，这里直接引入公式：

这里计算方差时少了一个 1/m0 项，m0 为属于该类的样本个数。但忽略此项不影响整体。
最后，我们可以综合考虑两个方面的公式，得到：

所以只要求 J 的最大值即可。又因为损失函数一般是找最小值，这里再对上述 J 公式进行变换（-max = min）得：

3、拉格朗日乘子法求解ω（算法）

这里拉格朗日乘子法的原理就不再赘述（高数学过），这里直接针对上述得到的损失函数使用此方法：

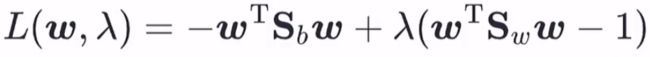
再对ω求偏导（这里又用到了矩阵求偏导的一些公式，这里不再赘述）：

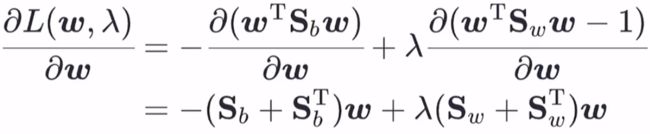
又因为 Sb 和 Sw 都是对称矩阵，所以转置后和原矩阵相同，则

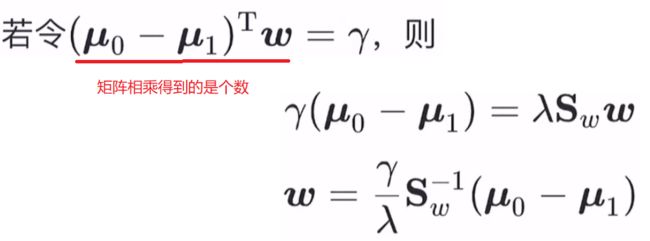
由于最终要求解的ω不关心其大小，只关心其方向，所以 γ/λ 这个常数项可以任意取值。我们取 γ/λ = 1，即得到 ω的解。

那此解是否为最小值点呢？因为 -ωT * Sb * ω 表示异类中心点的差的平方再取负，所以其值<=0 ，此目标函数值最大即为0，那么求得的 ω 代入目标函数只要不是 0 ，那就是最小值。

总结

第三章公式以及推导过程较多，其中一些数学知识（如矩阵函数求偏导）、信息论知识（信息熵、交叉熵）等之前可能没有接触过。但是总体上，跟着 机器学习三要素（模型、策略、算法）的思路走，一步步推导学习之后，也能够清楚的理解了。这里广义特征值和广义瑞利熵没有讲，后续补上。