7.5 SNN《脉冲神经网络研究进展综述》笔记

7.5 SNN《脉冲神经网络研究进展综述》笔记

一、SNN相关机制和结构

SNN的优势：丰富的时空动力学特征、多样的编码机制、契合硬件的事件驱动性等。

1.突触可塑性的生物学基础

赫布规则及其延伸

原始：当A细胞重复或持续地参与激活B细胞时，两个细胞间会发生某种生长过程或代谢变化，使得A细胞激活B细胞的效率得到提高。关于海马体中长时程增强作用（LTP）和长时程抑制作用（LTD）两种可塑性实验发现为赫布假说提供了支撑。

延伸：突触前-突触后的神经元发放顺序会引起LTP，突触后-突触前的神经元发放顺序会引起LTD。时间上存在的逻辑将会决定突触改变的方向和幅度。这种现象后来被称为STDP规则。

局限：赫布学习与STDP规则成功揭示了突触结构内权重的修改过程，但不足以解释突触个体的改变如何协调以实现神经系统的整体目标。下面将引入神经调质影响因素。

神经调质丰富了赫布规则

一些神经调质与奖励信号之间存在联系的例子：多巴胺神经元能够预估、检测奖励并相应地发出报警或激励信号，乙酰胆碱与去甲肾上腺素激素在处理新奇事物时的分泌有所增加。

神经调质能够调整它们所到之处的突触可塑性，作用形式可能是作为使能的门信号或是对于STDP窗口的形状和极性进行调整，同时多种神经调质组合在一起发挥不同作用，这为大脑在不同区域实现各异的神经元可塑性提供了生理基础。

神经调质作为突触前后神经元活动以外的第三种影响因素，公式描述如下：
$$\dot{w}=M\times H(pre,post)$$
$M$：表示神经调质的影响
$pre$：突触前神经元的输出脉冲（序列）
$post$：突触后神经元的脉冲相应或电位响应
$H$：突触活动在赫布规则下造成的预期影响或称为资格痕迹的可塑性变化暂态标记

三因子规则（无监督->监督）

赫布规则与STDP规则具有局部学习的特征，是脉冲神经网络模型中无监督算法模拟的重要对象，而神经调质的引入为微观上的突触结构变化与宏观上生物体适应性行为间建立了联系的桥梁，突触可塑性的变化因而具有了目的和方向。在整个神经网络功能优化的全局角度上，这样的三因子规则相较于原始赫布规则引入了监督性学习的特点，有力地推动了大脑深层网络的高效学习。

2.编码方式

生物对外界感知、自身内部环境的调节的行为反应最后都是以神经元短暂的脉冲序列实现信息的传递。信号通过动作电位与突触结构在神经元之间传播，信息以何种形式蕴藏在具有一定时空模式的脉冲序列中尚不明了。神经编码这一领域旨在解决这个问题。

常用神经编码方式：频率编码rc、时间编码tc、bursting编码、群编码pc。具体的脉冲在时间、振幅或形状上都可能有所不用，但在神经编码研究中，它们通常被视为相同的定型事件。

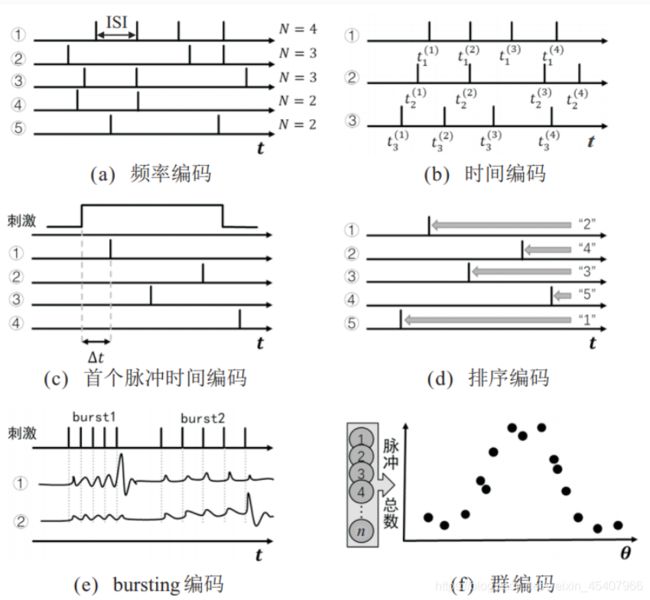
频率编码主要考察脉冲发放率（firing rate）。一般来说强烈的刺激将导致更为高频的脉冲序列，序列内部时间结构如内部脉冲间隔（ISI）不被考虑。频率编码被视为是对神经元输出的一种量化衡量，在经由训练好的ANN网络向SNN转换的相关工作中，可将脉冲发放率与ANN中连续的输出值等价，这也是该神经编码方式得到大量使用的原因。

时间编码更注重时间结构上的差异。除了完整的脉冲时间模式之外，从接受刺激到发放首个脉冲的时间以及脉冲之间的时序逻辑都被认为存在编码重要休息的可能。前者被称为首个脉冲时间编码，后者被称为排序编码。忽略时间结构仅仅计算脉冲数量的方式不利于信息的高效率传输。

Bursting是广泛存在于大脑中的一种神经元活动模式，指神经元在某段时间内密集、快速地激发脉冲，随后进入较长时间静息的行为。突触后神经元存在阈下膜电位共振现象，导致不同神经元针对bursting频率产生特异性选择，并可能为神经元间进行选择性通信提供了有效的编码机制。

群编码认为刺激产生的神经元信息是由多个神经元的联合活动表征的，比较著名的模型有群体向量模型。稀疏编码是群编码中较为特殊的一种，强调信息仅由较大群体中共同活跃的小部分神经元表达，且神经元数量可能远远大于输入信息的维度。

3.拓扑结构

主要还是神经网络的三大拓扑结构：全连接层、循环层、卷积层。

二、SNN的五个重点方向

1.神经元模型

神经元典型的结构按照信号传递的顺序为：树突（接受信号）、胞体（cpu）、轴突（发送信号至轴突末端的突触，传递到下一个神经元）。根据神经元工作时的电位动态特性建立相关模型，这构成了脉冲神经网路的基本单元。

积分泄漏发放模型及变体（LIF，有硬件电路出现）

1907提出Integrate-and-fire（I&F）模型，当时动作电位简述为膜电位达到阈值神经元激发脉冲，膜电位回落则回到静息值。模型针对阈下电位变化规律进行描述，最简单且常见的就是LIF模型：

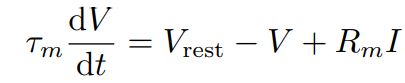
${\tau }_m$表示膜时间常数，$V_{rest}$表示静息电位，$R_m$表示细胞膜阻抗，$I$表示输入电流。
LIF简化了动作电位过程，保留了实际神经元膜电位泄露、积累、阈值激发这3个关键特征。在此基础上出现一些变体，如二阶LIF、指数LIF、自适应指数LIF等模型。这些变体模型更注重细节描述，以一定的代价增强LIF的生物可信度。

Izhikevich模型（有硬件电路出现）

该模型是具有生物合理性的H-H模型与计算高效的LIF模型之间的折中。采用了与LIF模型类似的动作电位描述方式，电势对H-H模型进行简化处理后得到。公式如下：
$$\frac{dV}{dt}=0.04V^2+5V+140-u+I$$
$$\frac{du}{dt}=a(bV-u)$$
$u$：一膜恢复变量，总体描述离子电流行为
$a、b$：分别用于调整$u$的时间尺度和关于膜电位$V$的敏感度
根据参数选择，该模型可以展示大脑皮层几乎所有已知神经元的放电模式，相比H-H模型，仿真所需要的计算开销约为百分之一。2004年时就可以支持10万个神经元规模网络的模拟。

Hodgkin-Huxley模型

1952年这两个人对乌贼巨轴突的电位数据进行研究，提出神经元电活动机制的理论数学模型和相关电路模拟，在动作电位的产生及传播机制方面做了奠基性贡献，后面拿到了诺贝尔奖，牛的。H-H模型主要是下面4个公式：

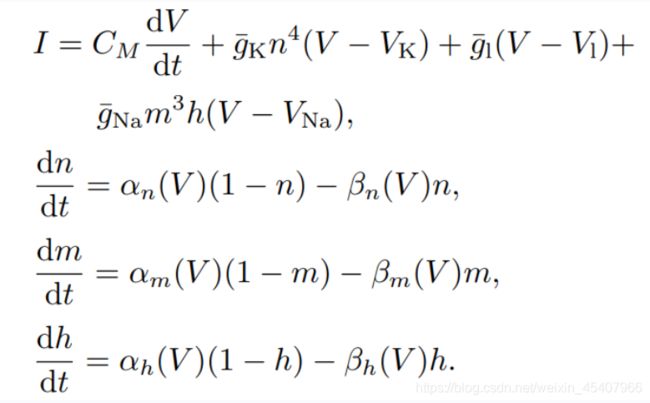
$I$：总膜电流密度
$V$： 膜电位
$C_M$：单位面积膜电容
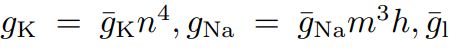这三个参数分别表示钾离子、钠离子和其他离子的电导密度
$V_K$、$V_{Na}$、$V_1$：各个离子通道的反转电位
$n$、$m$、$h$：假设为某几种与离子转运相关的粒子浓度，对应的$\alpha$和$\beta$代表该粒子向膜内膜外移动的速率
该模型中，各个离子通道与动作电位之间的产生机制被清晰地建模，并对生物神经组织实验记录的电位变化曲线有精确地近似。

脉冲响应模型（SRM）

基于LIF模型提出的一种更具有通用性的描述模型，它包含了不应期的模拟，采用了滤波器（有状态方程那味道）而非微分方程的形式描述电位变化。公式如下：

$\eta$：神经元自身在$t$时刻激发动作电位及随后连续的电位变化情形
$k$：对输入脉冲$I$的线性滤波器
${\gamma }_{ref}$：保证了一个绝对不应期的实现
${\theta }_i$、${\tau }_{\theta }$：根据实际生理数据进行优化调整
“脉冲相应”来源于$k$和$\eta$，分别描述神经元对输入脉冲和自身激发脉冲两个行为的相应。

目前需要研究的问题：

寻找兼具高生物可实现性、良好的网络学习能力以及超大规模集成电路构建能力的神经元模型。

2.训练算法

当前脉冲神经网络领域不存在公认的核心训练算法与技术（ANN中梯度下降是公认的网络优化理论基础）。生物合理性与任务表现间存在的不同侧重度、神经元模型和编码方式的不同造成了训练算法的多样性。根据训练过程是否使用标签可将训练算法概括性地划为有监督学习和无监督学习。无监督学习主要包括赫布规则和STDP两种突触可塑性规则的仿生学习算法，有监督学习可进一步划分为初期有监督学习算法和深度有监督学习算法。

有监督学习主要困难在于BP算法在脉冲神经网络中的应用。一方面BP算法自身缺乏生物合理性，突触信息传递的方向性使得前向传递和可能存在的反馈路径在生理上是分离的，目前不存在已知的方式来协调二者以实现反向传播中对前传权重的获取，这被称为weight transport问题；另一方面，SNN传递的信号为不可微的离散二值信号，脉冲形式的激活函数给基于梯度的优化算法的应用直接造成了困难。

（1）脉冲时间可塑性仿生学习算法（无监督，包括STDP、BCM、SWAT）

赫布规则 & STDP

根据两种突触可塑性规则可以设计仿生学习算法。常见描述公式如下：

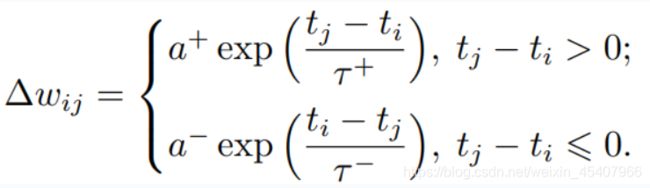
$\Delta w_{ij}$：权重改变量
$t_j、t_i$：突触前后神经元的脉冲发放时间
${\tau }^{+}、{\tau }^{-}$：影响STDP时间窗尺度的时间常数
$a^{+}、a^{-}$：分别对应LTP、LTD的两种权重变化方向
受到深度卷积网络的启发，有SNN的相关模型包含多层适用STDP规则的卷积层用于特征提取，最后一层的神经元不激发脉冲，而将最终的膜电位作为输出接入SVM中进行分类器有监督训练，在MNIST数据集上的准确率高达98.4%。

BCM

除了赫布规则和STDP规则之外，BCM是另外一种根据视觉皮层实验提出的突触可塑性规则。原始的赫布规则由于不包含突触连接的衰减机制或是增强阈值，所构建的模型并不具有稳定性。BCM规则在原始赫布规则基础上假定神经元具有决定突触权重改变方向的阈值，且阈值动态适应于神经元的历史活动，使得连接权重值最终能够达到稳态。其中神经元活动主要由脉冲发射率衡量，所以在BCM模型中多使用频率编码。

SWAT

SWAT结合了BCM规则中可变阈值的特点，为STDP可塑性窗口的形状施加了负反馈调节，增强了脉冲神经网络训练过程中的稳定性。在利用STDP和BCM训练输出层的同时，利用网络中的隐藏层作为频率滤波器，从输入脉冲时间序列中提取特征用于分类任务。

（2）初期有监督学习算法

SpikeProp & Multi-SpikeProp

SNN中，标签被编码为具有时序特征的目标脉冲序列，算法需要学习网络中的连接权重以实现对不同输入的特异性识别，并转换输出目标脉冲序列。2002年首次提出使用误差反向传播训练SNN学习目标脉冲的有监督算法SpikeProp，该算法使用时间编码和SRM模型，通过线性处理神经元接收的输入和由此产生的脉冲发放时间的关系，绕过在阈值处产生的不连续性问题，最小化由目标脉冲与实际脉冲时间之差定义的误差函数。然而该算法也存在神经元长时间静息后突触权重无法保持以及单次仿真过程中每个神经元仅允许输出一个脉冲的限制，其中后者明显降低了神经元信息表达的丰富性。随后Multi-SpikeProp被提出，将神经元扩展至使用多个脉冲传递信息的形式。

ReSuMe

ReSuMe代表了一种与经典的Widrow-Hoff算法相类似的方法，该算法使用基于速率的神经元模型，在不需要显式梯度计算的情况下，最小化输出与目标信号之间的差距，目标是构建神经网络所需的输入输出特性。它结合了赫布规则和远程监控，其中远程监控指的是目标信号并不直接传递给受训练的神经元，而是与突触前神经元共同决定突触权重的变化。在Widrow-Hoff规则中，针对输入$x_i$，期望输入$y_d$以及实际输出$y_o$，权重更新表达式为
$$\Delta w_{oi}=\alpha x_i(y_d-y_o)$$
考虑引入时间维度以及脉冲形式后，ReSuMe的学习规则可重写为
$$\frac{d{w}_{oi}(t)}{dt}=[S_d(t)-S_o(t)][a_d+{\int }_0^{\infty }{a}_{di}(s)S_i(t-s)ds]$$
$S_i(t)、S_o(t)、S_d(t)$：输入、输出、期望的脉冲序列
$a_d$：用于调节权重变化的平均强度
包含$a_{di}(s)$的赫布规则项起到实际精确调节脉冲时间的功能
$s$：表示产生输出时相对输入的时间间隔
期望信号与输入相互作用与实际输出相对独立，不对输出神经元有直接的影响，体现出ReSuMe的远程监督特性。该算法能够有效地在特定输入下学习产生预期信号，输出的信号可用于分类任务。下面是ReSuMe规则的示意图。

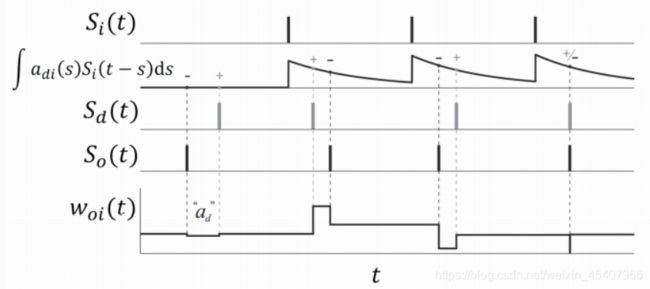
tempotron & chronotron

chronotron神经网络可以产生在时间上精确符合预期的脉冲序列。tempotron作为其前身，受限于单个脉冲输出的限制，无法编码足够多的信息在多个tempotron形成的网络之间的传递。针对脉冲序列的差异，chronotron采用VP距离作为损失函数构建的依据，提出E-learning和I-learning两种学习规则，前者基于梯度下降方法，后者相对更具有生物合理性。chronotron中损失函数定义如下

$F、F$：实际脉冲序列和目标脉冲序列
$t^f、t^f$：不同序列中的第$f$个脉冲
$F^{\ast }、F^{\ast }$：实际脉冲需要删除的脉冲序列、目标脉冲需要加入的脉冲序列
$u$：用来衡量膜电位
${\gamma }_d、{\tau }_q$：两个正参数
E-learning权重更新规则如下

$\gamma$：学习率
$\lambda$：由该突触输入导致的突触后电位的变化
由于脉冲增删实际上为一个离散过程，E-learning采用分段梯度下降对损失函数进行最小化。$I-learning$在此基础上参照ReSuMe，调整权重规则为局部可计算的突触电流形式如下

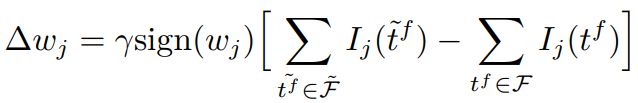
chronotron表现出在200ms时长的不同输入序列下以亚毫秒级的时间误差学习目标脉冲序列的能力。

SPAN（spike pattern association neuron）

这也是一种以有监督方式训练神经元学习所需输入-输出脉冲映射关系的算法。它将脉冲信号与特定的核函数进行卷积，转换为模拟信号，使得Widrow-Hoff规则可以在转换后的信号上直接应用以调整突触权重。核函数举例如下

其多用于突触后电位变化的模拟，效果是把兴奋性突触后点位的连续变化替代单次脉冲进行计算。
修改后的Widow-Hoff规则可写为
$$\Delta w_i=\lambda {\int }_0^{\infty }{x}_i(t)(y_d(t)-y_{out}(t))dt$$
之前的离散表达式中的各个变量转换为核函数下的连续信号$x_i、y_d、y_{out}$

（3）深度有监督脉冲神经网络

主要包含以转换SNN为代表的间接监督性学习算法和以时空反向传播为代表的直接监督性算法。其中“间接监督性”体现在有监督信号仅在向SNN转换前的原始模型中进行训练这一点上。

转换SNN（ANN-converted SNN）

转换SNN的基本理念是在使用ReLU函数的ANN网络中，连续的激活函数值可以由SNN中频率编码下的平均脉冲发放率近似，在完成原始ANN训练后，再通过特定的手段将其转换为SNN。本质上，转换SNN训练所依赖的仍然是ANN中进行的反向传播算法。就性能来说，转换SNN保持着与ANN发展进程最小的差距，并具有在大规模的网络结构与数据集上实现的能力。许多学者在VGG-16、GoogLeNet、ImageNet数据集得到较高准确率。
但是为了方便转换，很多工作需要对原始的ANN模型进行约束，例如将偏置固定为0、无法用批归一方法、只能用平均池化而非最大池化。这些约束都使得转换后SNN的调整更复杂且可能潜在造成更大的性能损失。另外，转换过程中增加I&F神经元的阈值后需要对阈值和权重进行重新平衡，过低的阈值使得神经元易于激发而丧失特异性，反之则会使得脉冲较难激发，深层网络的仿真步数大幅增加。

2019年有人提出了“磨刀石”（whetstone）的新颖SNN转换方式：在ANN网络中采用有界ReLU函数作为激活函数，在完成最初的网络训练后，逐层进行有界ReLU函数向阶跃函数的渐进式转换，在观察到一定性能下降时重启对网络的训练，完整训练流程结束后便得到对应的SNN网络。与针对完整网络进行单次转换，这种渐进的方式能够减缓转换带来的性能损失。但目前该方法得到的SNN仅使用单步仿真时长，在性能上表现不佳，SNN本身在时域上可能的动态特性以及处理能力无法得到进一步的发掘与利用。

除了对原始ANN施加约束造成的性能下降外，转换SNN完成一次前向推理通常需要几百甚至几千时间步的模拟，造成额外的延迟和能耗。也有工作尝试结合转换SNN与直接训练算法，将转换SNN作为一种权重初始化手段并接受直接算法的后续训练，以期得到低时间步下的高性能表现。

转换SNN的最大弊端在于是其大多专注于发展新结构的转换方法和缩小与ANN之间的性能差异，而不在于对SNN特质的研究，这对SNN发展的直接推动较为有限。

直接训练算法

由于BP算法在ANN上的成功，不少工作开始考虑将BP用于SNN端对端直接训练的可能性。关于weight transport问题，研究者们发现反向连接对前传权重的精确获取对于BP算法的有效实施并不是必要的。通过将误差信号乘以随机权重实行的RBP（random backpropagation）并不会显著影响学习的表现，这对误差信号在大脑中的利用形式提出新的见解，适应性脉冲形式的RBP也出现了。

BP过程面临的主要问题还是脉冲函数可导性质的缺乏，目前常用解决方案是采用与之相近的连续函数对脉冲函数或其导数进行替代，进而产生基于脉冲的反向传播算法。在具体函数形式选择与算法实现上，直接训练算法表现出多样化特征（这里有很多例子就不一一阐述了）。
现有的直接训练算法在深层结构上的应用仍有待探索。SNN与ANN的发展现状存在一定差距，一方面因为当前编程框架下SNN额外的时间维度将造成数倍于同规模ANN的训练现存需要，还由于阈值激发特性于脉冲的稀疏性，当SNN趋于深层时仿真周期变长，这将进一步提升对显存的需求；另一方面，深层网络训练难点（如梯度消失）在SNN中同样存在，并且部分利于深度神经网络训练的技巧在SNN上进行简单移植时将破坏其保有的优势特征（例如归一化手段在SNN中无法得到保证）。以上所述即可看出SNN无法在大规模数据集上获得足够令人信服的证据表现。

（4）其他脉冲神经网络学习算法

液体机（LSM）

生物神经网络建模的一个关键问题是怎样对多模态的连续时空输入进行实时处理。2002年提出的LSM提供了一种可行的计算模型。液体状态机由输入层、液体层和输出层组成。输入层接受模拟输入或离散的脉冲输入，并与所有的液体层神经元相连。液体层由大量LIF神经元构成的循环结构组成，连接的方向和权重随机指定，它们接受输入并最终映射至该层所有神经元的放电状态。循环连接的存在使网络具有了记忆性质，放电状态包含了当前与历史输入的信息。LSM两个宏观性质构成了它具有实时计算能力的充要条件：分离特性和逼近特性。分离特性描述了两个不同输入流引起的系统内部状态轨迹之间距离的大小；逼近特性描述输出机制的分辨和重编码能力，能够区分液体的不同内部状态并将其转换为给定的目标输出。LSM具有记忆与动态输入流实时处理的能力，令其在语音识别、轨迹预测等方面获得了应用。

深度信念网络（DBN）

DBN是一种概率生成式模型，由多层受限玻尔兹曼机堆叠组成，采用对比散度算法高效近似最大似然法进行逐层无监督训练。在完成无监督预训练后，可以在DBN上增加一层包含监督信号的网络，利用BP算法将误差信息自顶向下传播至每一层RBM，对无监督过程中初始化的权重进行进一步微调。DBN克服了当时深层BP网络因随机初始化权值而陷入局部最优和训练耗时长的缺点，首先提出了真正行之有效的深度结构训练方法，并在MNIST上取得了优于支持向量机的结果。但是，DBN由于相对于深度学习方法在精度上表现欠佳，总体上不再受学者的青睐。脉冲DBN的优势主要继承于神经形态硬件，而其本身对脉冲特性的契合相比之下并不见长。

（5）存在问题并且需要进一步研究的点：

SNN在超大超深层的网络训练算法上，面临着脉冲信号如何编码、梯度消失、训练资源开销大、算法收敛性等问题。所以说，研究超大超深层SNN网络的编码方式和匹配的训练算法是需要研究的问题。

3.编程框架

BindsNET、Spyketorch。搭建一个大的SNN网络需要非常好的编程功底。

4.数据集

简要说明

适合SNN的数据集由时空事件流构成，如Neuromorphic-MNIST、N-Caltech101、DVS-CIFAR10、DVS-Gesture。这些数据集都比较小。所以说，发展更大规模且更加契合SNN时空处理能力的数据集将成为SNN发展的驱动力之一。

神经形态数据集

受神经形态视觉传感器成像机制启发所产生的数据集被认为是目前最适合SNN应用的一类数据集。

神经形态视觉传感器是受生物视觉处理机制启发，捕捉视野中的光强变化产生异步时间流的一类传感器，具有代表性的神经形态视觉传感器有动态视觉传感器DVS及动态主动成像传感器DAVIS等。此类动态传感器主要关注视野中的变化特征而自动忽略背景中静态无关的信息，这也使得该类传感器具有低延迟、异步、稀疏的相应特征和快速、高动态频率的特性，在光流估计、目标跟踪、动作识别等方向均有应用。由此类传感器产生的数据集被称为神经形态数据集，数据一般由四维向量组成$(x,y,t,p)$。$(x,y)$记录成像的拓扑坐标，$t$记录脉冲产生时间信息，$p$记录脉冲的极性。

目前的神经形态数据集可以分为三类：实地场景采集得到的数据集、由数据集转换得到的数据集、生成数据集。第一类数据集生成的是无标签的数据，贴近实际应用场景，可用于追踪和检测、光流估计、3D场景重构、手势识别。但是由于使用者对第一类数据集的预处理方式不统一，使结果很难公平地比较。第二类数据集由带标签的静态图像数据集通过神经形态传感器实拍生成，主要由已被广泛研究的、用于传统非脉冲任务的数据集转换得到。一般是先固定一张静态的图片，再用动态传感器沿指定的方向平移产生相应数据的脉冲事件流版本。转换数据集和原始数据集具有一定的特征相似性，此类数据集易于使用和评估，用得最为广泛。第三类数据集主要利用带标签的数据，通过算法模拟动态视觉传感器特性，进而生成得到。算法模拟时可以间接利用视频中相邻帧的差分等信息。这类数据集避免了数据采集所需要的大量工程实验，但也无法高分辨地模拟数据的事件驱动特性。第二、三类数据集由原始数据二次转换，其数据很难表达丰富的时序信息。

5.硬件芯片

SNN在硬件电路上具有超低能耗实现的优势。具体一些电路设计在此忽略。

6.展望

1.当前许多SNN算法仅对频率编码给予关注，这一编码方式无视于序列内部的时间结构，无法发挥SNN在时域信息处理上的优势。因此适应于高信息密度时间编码算法设计是目前有待探索的方向。

2.现有的算法在生物合理性与性能表现、模型容量之间始终存在矛盾。有学者提出BP-STDP算法希望获得兼具可塑性规则的生物合理性与梯度下降方法最优性训练能力的综合算法，但究其本质，并不具有STDP局部学习与时间依赖的特点，内核仍然是梯度下降方法。对生物合理性与性能表现、模型容量两方面的有机结合依然会是SNN算法领域不懈的追求。

3.SNN在真正大规模的深层网络训练算法上仍有亟待填补的空白。STBP等直接训练算法在仿真周期、模型性能以及网络规模上综合表现较优，有可能是未来SNN训练算法持续发展的途径。但是，在深度神经网络训练中存在的梯度消失、资源开销大甚至算法不收敛等问题都有待于进一步确认与探讨。

4.SNN神经元所具有的阈值发放特性可能使其对模型压缩算法具有更高的接受度，因此，与权重量化、剪枝等压缩算法的结合也有待探索。

5.在神经形态器件自身进行架构创新、继续追求更高能效的基础上，针对现有硬件平台探索各种优势技术的结合，则是另一个需要深入钻研的重要方向。