matlab偏微分方程工具箱求解

Matlab的偏微分方程工具箱求解方法

这一节我们主要用matlab自带的偏微分方程的工具箱函数求解

一.偏微分方程组的matlab求解语句

​ 该命令用以求解以下的$PDE$方程式：
$$c(x,t,u,\frac{\partial u}{\partial x})\frac{\partial u}{\partial t}=x^{-m}\frac{\partial (x^{m}f(x,t,u,\frac{\partial u}{\partial x}))}{\partial x}+s(x,t,u,\frac{\partial u}{\partial x})$$
​ 其中：$t\in [t_0,t_f],x\in [a,b]$。偏微分方程的初解：
$$u(x,t_0)=v_0(x)$$
​ 边界条件为：
$$p(x,t,u)+q(x,t)f(x,t,u,\frac{\partial u}{\partial x})=0$$
​ 下面介绍求解此类方程的函数用法：
$$sol=pdepe(m,pdepe,icfun,bcfun,xmesh,tspan,options);$$
​ $m:$对称参数。

​ $xmesh:$位置向量,$xmesh=[x_0,x_1,...x_N],x_0=a,x_N=b$。

​ $tspan:$时间变量$t$的向量，$tspan=[t_0,t_1,...t_M],t_0=t_0,t_M=t_f$。

​ $pdefun:$用户提供的$pde$函数文件。函数格式如下:
$$[c,f,s]=pdefun(x,t,u,dudx);$$
​ 也就是说我们要自己设置相应的输出$c,f,s$，且它们都是行向量。

​ $icfun:$求解$u$的起始值，格式为$u=icfun(x)$。且$u$是行向量。

​ $bcfun:$提供边界条件函数，格式：
$$[pl,ql,pr,qr]=bcfun(xl,ul,xr,ur,t);$$
​ $pl,ql:$左边界$p$和$q$的行向量。$pr,qr:$右边界$p$和$q$的行向量。

​ $options:$求解器相关解法参数，见$odeset$。

​ $sol:$多维向量输出，$sol(:,:,i)$为$u_i$的输出，而$u_i(j,k)=sol(j,k,i)$表示在$t=tspan(j),x=xmesh(k)$时候 的$u_i$的值。

​ 要获得特定位置和时间的解用以下命令：
$$[uout,duoutdx]=pdeval(m,xmesh,ui,xout);$$
​ $xmesh:[x_0,x_1,...x_N]$

​ $ui:sol(j,:,i),$第$i$个输出$u_i$在时间$t_j$处的解。

​ $uout:$在指定$t_f$下对应指定位置$xout$的值。

​ $duoutdx:$相对应的$\frac{du}{dx}$。

二.具体的用法

​ 1.求解以下偏微分方程(解析解为 $u(x,t)=e^{-t}sin(\pi x)$)：
$${\pi }^2\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial x^2}$$
​ 其中$x\in [0,1]$,满足以下条件:
$$\begin{gathered} u(x,0)=sin(\pi x) \\ u(0,t)=0 \\ \pi e^{-t}+\frac{\partial u(1,t)}{\partial x}=0 \end{gathered}$$

​ $solve:$

​ 改写以上偏微分方程到标准形式：
$${\pi }^2\frac{\partial u}{\partial t}=x^0\frac{\partial }{\partial x}(x^0\frac{\partial u}{\partial x})+0$$
​ 具体的实现代码如下:

function first
    %计算从t:0~3的值
    x = linspace(0,1,20);
    t = linspace(0,3,60);
    subplot(121);
    sol = pdepe(0,@firstPdefun,@firstIcfun,@firstBcfun,x,t);
    u = surf(x,t,sol(:,:,1));
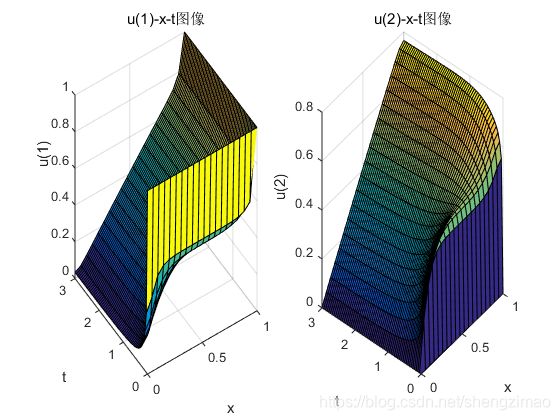
    title('微分方程数值解');
    xlabel('x');
    ylabel('t');
    zlabel('u')
    subplot(122);
    [X,T] = meshgrid(x,t);
    U = exp(-T).*sin(pi*X);
    surf(X,T,U);
    title('微分方程解析解');
end

%方程段
function [c,f,s] = firstPdefun(x,t,u,dudx)
    c = pi^2;
    f = dudx;
    s = 0;
end
%起始值条件段
function u = firstIcfun(x)
    u = sin(pi*x);
end
%边界条件段
function [pl,ql,pr,qr] = firstBcfun(xl,ul,xr,ur,t);
    pl = ul;
    ql = 0;
    pr = pi*exp(-t);
    qr = 1;
end

对比一下发现几乎和解析解一摸一样！

2.求解以下偏微分方程的数值解：
$$\begin{gathered} \frac{\partial u_1}{\partial t}=0.024\frac{{\partial }^2{u}_1}{\partial x^2}-F(u_1-u_2) \\ \frac{\partial u_2}{\partial t}=0.170\frac{{\partial }^2{u}_2}{\partial x^2}+F(u_1-u_2) \\ F(u_1-u_2)=e^{5.73(u_1-u_2)}-e^{-11.46(u_1-u_2)} \end{gathered}$$
初值条件:
$$\begin{gathered} u_1(x,0)=1 \\ {u}_2(x,0)=0 \end{gathered}$$
边值条件:
$$\begin{gathered} \frac{\partial u_1(0,t)}{\partial x}=0 \\ {u}_2(0,t)=0 \\ {u}_1(1,t)=1 \\ \frac{\partial u_2(1,t)}{\partial x}=0 \end{gathered}$$
$Solve:$

​ 化简上面的偏微分方程为标准形式：
$${\left(\begin{array}{c}1\\ 1\end{array}\right)}_{.}\ast \frac{\partial }{\partial t}\left(\begin{array}{c}{u}_1\\ u_2\end{array}\right)=\frac{\partial }{\partial x}\left(\begin{array}{c}0.024\frac{\partial u_1}{\partial x}\\ 0.170\frac{\partial u_2}{\partial x}\end{array}\right)+\left(\begin{array}{c}-F(u_1-u_2)\\ F(u_1-u_2)\end{array}\right)$$
​ 化简左边界条件也有：
$$\left(\begin{array}{c}0\\ u_2\end{array}\right)+{\left(\begin{array}{c}1\\ 0\end{array}\right)}_{.}\ast \left(\begin{array}{c}0.024\frac{\partial u_1}{\partial x}\\ 0.170\frac{\partial u_2}{\partial x}\end{array}\right)=\left(\begin{array}{c}0\\ 0\end{array}\right)$$
​ 化简右边界条件有：
$$\left(\begin{array}{c}{u}_1-1\\ 0\end{array}\right)+{\left(\begin{array}{c}0\\ 1\end{array}\right)}_{.}\ast \left(\begin{array}{c}0.024\frac{\partial u_1}{\partial x}\\ 0.170\frac{\partial u_2}{\partial x}\end{array}\right)=\left(\begin{array}{c}0\\ 0\end{array}\right)$$
​ 最后附上整个代码：

function second
xmesh  = linspace(0,1,20);
tspan = linspace(0,3,60);
sol = pdepe(0,@secondPdefun,@secondPdein,@secondPdebc,xmesh,tspan);
subplot(121);
surf(xmesh,tspan,sol(:,:,1));
xlabel('x');
ylabel('t');
zlabel('u(1)');
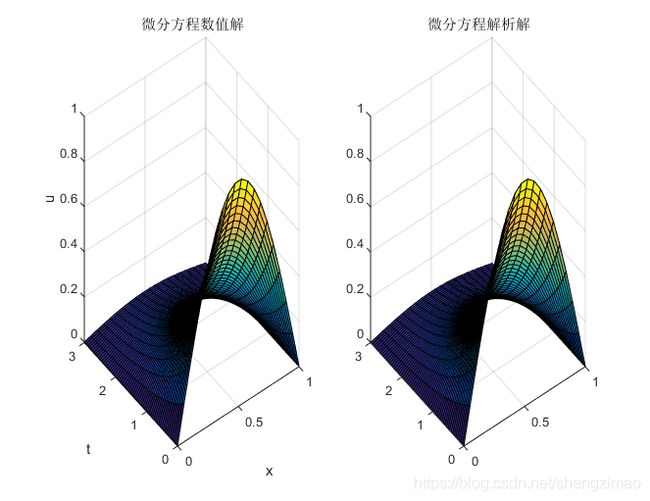
title('u(1)-x-t图像');
subplot(122);
surf(xmesh,tspan,sol(:,:,2));
xlabel('x');
ylabel('t');
zlabel('u(2)');
title('u(2)-x-t图像');
end

function [c,f,s] = secondPdefun(x,t,u,dudx)
c = [1 1]';
f = [0.024*dudx(1) 0.170*dudx(2)]';
y = u(1) - u(2);
stemp = exp(5.73*y) - exp(-11.46*y);
s = [-stemp stemp]';
end

function up = secondPdein(x,t,u,dudx)
up = [1 0]';
end

function [pl ql pr qr] = secondPdebc(xl,ul,xr,ur,t)
pl = [0 ul(2)]';
ql = [1 0]';
pr = [ur(1)-1 0]';
qr = [0  1]';
end

最后的结果是：