【Pytorch学习笔记2】Pytorch的主要组成模块

个人笔记，仅用于个人学习与总结
感谢DataWhale开源组织提供的优秀的开源Pytorch学习文档：原文档链接

1. Pytorch的主要组成模块

1.1 完成深度学习的必要部分

机器学习步骤：

1. 对数据预处理，包括数据格式统一和数据变换。同时划分训练集、数据集；
2. 选择模型，设定损失函数和优化方法与相对应的超参数(可以使用sklearn这样的机器学习库模型中自带的损失函数和优化器)；
3. 最后用模型拟合训练集数据，并在验证集上计算结果。

步骤具体分析：

1. 代码实现：深度学习所需样本量大，一次加载所有数据会导致内存量不足；同时批(batch)训练等提高模型表现的策略，需要每次训练读取固定数量样本送入模型训练。深度学习在数据加载上需要有专门的设计；
2. 模型实现：深度学习网络层数较多，且有一些用于实现特定功能的层(卷积层、池化层、拟正则化层、LSTM层)，深度神经网络需要“逐层”搭建，或者预先定义可实现特定功能的模块，再把这些模块组装起来。
3. 损失函数和优化器的设定：与经典机器学习的实现类似，损失函数和优化器要能够保证方向传播能够在用户自行定义的模型结构上实现。
4. 深度学习中训练和验证过程最大的特点在于读入数据是按批的，每次读入一个批次的数据，放入GPU中训练，然后将损失函数反向传播回网络最前面的层，同时使用优化器调整网络参数。这里会涉及到各个模块配合的问题。训练/验证后还需要根据设定好的指标计算模型表现。

1.2 基本配置

导入必需的库：
注意这里只是建议导入的包导入的方式，可以采用不同的方案，比如涉及到表格信息的读入很可能用到pandas，对于不同的项目可能还需要导入一些更上层的包如cv2等。如果涉及可视化还会用到matplotlib、seaborn等。涉及到下游分析和指标计算也常用到sklearn。

import os
import numpy as np
import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader
import torch.optim as optimizer

超参数的设置：
可以统一设置以下超参数(开始学习过程前设置的参数)，方便后续调试：

• batch size
• 初始学习率
• 训练次数(max_epochs)
• GPU配置

batch_size = 16
# 批次的大小
lr = 1e-4
# 优化器的学习率
max_epochs = 100

GPU的设置
有两种常见模式：

# 方案一：使用os.environ，这种情况如果使用GPU不需要设置
os.environ['CUDA_VISIBLE_DEVICES'] = '0,1'

# 方案二：使用“device”，后续对要使用GPU的变量用.to(device)即可
device = torch.device("cuda:1" if torch.cuda.is_available() else "cpu")

1.3 数据读入

Pytorch读入数据是通过Dataset+DataLoader的方式完成的。Dataset定义好数据的格式，DataLoader用iterative的方式不断读入批次数据。
可以通过自定义Dataset类来实现灵活的数据读取，定义的类主要包含三个函数：

• __init__：用于向类中传入外部参数，同时定义样本集；
• __getitem__：用于逐个读取样本集合中的元素，可以进行一定的变换，并将返回训练/验证所需的数据；
• __len__：用于返回数据集的样本数。

例子1
以cifar10数据集为例

import torch
from torchvision import datasets
train_data = datasets.ImageFolder(train_path, transform=data_transform)
val_data = datasets.ImageFolder(val_path, transform=data_transform)

这里使用了PyTorch自带的ImageFolder类的用于读取按一定结构存储的图片数据（path对应图片存放的目录，目录下包含若干子目录，每个子目录对应属于同一个类的图片）。
其中“data_transform”可以对图像进行一定的变换，如翻转、裁剪等操作，可自己定义。
例子2
该例子中图片存放在一个文件夹，另外有一个csv文件给出了图片名称对应的标签，这种情况下需要自己定义Dataset类：

class MyDataset(Dataset):
    def __init__(self, data_dir, info_csv, image_list, transform=None):
        """
        Args:
            data_dir: path to image directory.
            info_csv: path to the csv file containing image indexes
                with corresponding labels.
            image_list: path to the txt file contains image names to training/validation set
            transform: optional transform to be applied on a sample.
        """
        label_info = pd.read_csv(info_csv)
        image_file = open(image_list).readlines()
        self.data_dir = data_dir
        self.image_file = image_file
        self.label_info = label_info
        self.transform = transform

    def __getitem__(self, index):
        """
        Args:
            index: the index of item
        Returns:
            image and its labels
        """
        image_name = self.image_file[index].strip('\n')
        raw_label = self.label_info.loc[self.label_info['Image_index'] == image_name]
        label = raw_label.iloc[:,0]
        image_name = os.path.join(self.data_dir, image_name)
        image = Image.open(image_name).convert('RGB')
        if self.transform is not None:
            image = self.transform(image)
        return image, label

    def __len__(self):
        return len(self.image_file)

构建好Dataset后，就可以使用DataLoader来按批次读入数据了，实现代码如下：

from torch.utils.data import DataLoader

train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size, num_workers=4, shuffle=True, drop_last=True)
val_loader = torch.utils.data.DataLoader(val_data, batch_size=batch_size, num_workers=4, shuffle=False)

其中：

• batch_size：每次读入的样本数；
• num_workers：有多少个进程用于读取数据；
• shuffle：是否将读入的数据打乱；
• drop_last：对于样本最后一部分没有达到批次数的样本，使其不参与训练。

DataLoader的读取可以用next和iter完成：

import matplotlib.pyplot as plt
images, labels = next(iter(val_loader))
print(images.shape)
plt.imshow(images[0].transpose(1,2,0))
plt.show()

1.4 模型构建

1.4.1 神经网络的构造

Module类是nn模块里提供的一个模型构造类，是所有神经⽹网络模块的基类，我们可以继承它来定义我们想要的模型。下面继承Module类构造多层感知机。这里定义的MLP类重载了Module类的init函数和forward函数。它们分别用于创建模型参数和定义前向计算。前向计算也即正向传播。

import torch
from torch import nn

class MLP(nn.Module):
  # 声明带有模型参数的层，这里声明了两个全连接层
  def __init__(self, **kwargs):
    # 调用MLP父类Block的构造函数来进行必要的初始化。这样在构造实例时还可以指定其他函数
    super(MLP, self).__init__(**kwargs)
    self.hidden = nn.Linear(784, 256)
    self.act = nn.ReLU()
    self.output = nn.Linear(256,10)
    
   # 定义模型的前向计算，即如何根据输入x计算返回所需要的模型输出
  def forward(self, x):
    o = self.act(self.hidden(x))
    return self.output(o)   

---

代码注释：

1. **kwargs允许将不定长度的键值对作为参数传递给函数，若想在函数里处理带名字的参数，需要使用``kwargs。

def greet_me(**kwargs):
    for key, value in kwargs.items():
        print("{0} == {1}".format(key, value))


>>> greet_me(name="yasoob")
name == yasoob

2. torch.nn.Linear(in_features, out_features, bias=True)是网络中定义全连接层的函数，两个参数分别为输入、输出的二维张量大小，也代表了该全连接层的神经元个数。bias表示是否存在偏差值。
3. super(MLP, self).__init__(**kwargs)用于调用父类的方法。

#!/usr/bin/python
# -*- coding: UTF-8 -*-
 
class FooParent(object):
    def __init__(self):
        self.parent = 'I\'m the parent.'
        print ('Parent')
    
    def bar(self,message):
        print ("%s from Parent" % message)
 
class FooChild(FooParent):
    def __init__(self):
        # super(FooChild,self) 首先找到 FooChild 的父类（就是类 FooParent），然后把类 FooChild 的对象转换为类 FooParent 的对象
        super(FooChild,self).__init__()    
        print ('Child')
        
    def bar(self,message):
        super(FooChild, self).bar(message)
        print ('Child bar fuction')
        print (self.parent)
 
if __name__ == '__main__':
    fooChild = FooChild()
    fooChild.bar('HelloWorld')

Parent
Child
HelloWorld from Parent
Child bar fuction
I'm the parent.

4. __init__()中定义了两个全连接层，forward()中定义了模型的前向计算，将各个层连接起来。

参考文献：
python进阶-**kwargs
super()方法

---

以上的 MLP 类中无须定义反向传播函数。系统将通过自动求梯度而自动生成反向传播所需的 backward 函数。

我们可以实例化 MLP 类得到模型变量 net 。下面的代码初始化 net 并传入输入数据 X 做一次前向计算。其中， net(X) 会调用 MLP 继承自 Module 类的 call 函数，这个函数将调用 MLP 类定义的forward 函数来完成前向计算。

X = torch.rand(2,784)
net = MLP()
print(net)
net(X)

MLP(
  (hidden): Linear(in_features=784, out_features=256, bias=True)
  (act): ReLU()
  (output): Linear(in_features=256, out_features=10, bias=True)
)
tensor([[ 0.0149, -0.2641, -0.0040,  0.0945, -0.1277, -0.0092,  0.0343,  0.0627,
         -0.1742,  0.1866],
        [ 0.0738, -0.1409,  0.0790,  0.0597, -0.1572,  0.0479, -0.0519,  0.0211,
         -0.1435,  0.1958]], grad_fn=<AddmmBackward>)

注意：这里并没有将 Module 类命名为 Layer (层)或者 Model (模型)之类的名字，这是因为该类是一个可供⾃由组建的部件。它的子类既可以是⼀个层(如PyTorch提供的 Linear 类)，又可以是一个模型(如这里定义的 MLP 类)，或者是模型的⼀个部分。

1.4.2 神经网络中常见的层

深度学习的一个魅力在于神经网络中各式各样的层，例如全连接层、卷积层、池化层与循环层等等。虽然PyTorch提供了大量常用的层，但有时候我们依然希望⾃定义层。

• 不含模型参数的层

我们先介绍如何定义一个不含模型参数的自定义层。下面构造的 MyLayer 类通过继承 Module 类自定义了一个将输入减掉均值后输出的层，并将层的计算定义在了 forward 函数里。这个层里不含模型参数。

import torch
from torch import nn

class MyLayer(nn.Module):
    def __init__(self, **kwargs):
        super(MyLayer, self).__init__(**kwargs)
    def forward(self, x):
        return x - x.mean() 

测试结果，实例化该层，然后做前向计算：

layer = MyLayer()
layer(torch.tensor([1, 2, 3, 4, 5], dtype=torch.float))

tensor([-2., -1.,  0.,  1.,  2.])

• 含模型参数的层

我们还可以自定义含模型参数的自定义层。其中的模型参数可以通过训练学出。

Parameter类其实是 Tensor 的子类，如果一个 Tensor 是 Parameter ，那么它会自动被添加到模型的参数列表里。所以在自定义含模型参数的层时，我们应该将参数定义成 Parameter ，除了直接定义成 Parameter 类外，还可以使用 ParameterList 和 ParameterDict 分别定义参数的列表和字典。

class MyListDense(nn.Module):
    def __init__(self):
        super(MyListDense, self).__init__()
        self.params = nn.ParameterList([nn.Parameter(torch.randn(4, 4)) for i in range(3)])
        self.params.append(nn.Parameter(torch.randn(4, 1)))

    def forward(self, x):
        for i in range(len(self.params)):
            x = torch.mm(x, self.params[i])
        return x
net = MyListDense()
print(net)

class MyDictDense(nn.Module):
    def __init__(self):
        super(MyDictDense, self).__init__()
        self.params = nn.ParameterDict({
                'linear1': nn.Parameter(torch.randn(4, 4)),
                'linear2': nn.Parameter(torch.randn(4, 1))
        })
        self.params.update({'linear3': nn.Parameter(torch.randn(4, 2))}) # 新增

    def forward(self, x, choice='linear1'):
        return torch.mm(x, self.params[choice])

net = MyDictDense()
print(net)

---

代码解析：

1. torch.mm将两个张量相乘。
2. ParameterList将输入的元素为Parameter的列表转换成ParameterList，ParameterDict则将输入的参数字典转换成专门的字典。
3. 含参数模型的层，个人认为是通过自定义参数与前向传播计算方法，将参数加入到学习的数据中。

参考文献：
Pytorch学习(3) —— nn.Parameter nn.ParameterList nn.ParameterDict 源码解析
PyTorch中的torch.nn.Parameter() 详解

---

• 二维卷积层

二维卷积层将输入和卷积做互相关运算，并加上一个标量偏差来得到输出。卷积层的模型参数包括了卷积核和标量偏差。在训练模型的时候，通常我们先对卷积核随机初始化，然后不断迭代卷积核和偏差。

import torch
from torch import nn

# 卷积运算（二维互相关）
def corr2d(X, K): 
    h, w = K.shape
    X, K = X.float(), K.float()
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i: i + h, j: j + w] * K).sum()
    return Y

# 二维卷积层
class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super(Conv2D, self).__init__()
        self.weight = nn.Parameter(torch.randn(kernel_size))
        self.bias = nn.Parameter(torch.randn(1))

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

---

代码解析：

1. tensor.float()数据转换，K为卷积核，X为输入信号；
2. corr2d卷积运算函数；
3. 卷积层参数的选择，自定义kernel_size与卷积核大小相同的参数与偏差值bias。前向运算定义为参数weight与输入信号的卷积运算再加上偏差。

参考文献：

---

卷积窗口形状为$p\times q$的卷积层称为$p\times q$卷积层。同样，$p\times q$卷积或$p\times q$卷积核说明卷积核的高和宽分别为$p$和$q$。

填充(padding)是指在输⼊高和宽的两侧填充元素(通常是0元素)。
例子
下面的例子里我们创建一个高和宽为3的二维卷积层，然后设输入高和宽两侧的填充数分别为1。给定一个高和宽为8的输入，我们发现输出的高和宽也是8。

import torch
from torch import nn

# 定义一个函数来计算卷积层。它对输入和输出做相应的升维和降维
import torch
from torch import nn

# 定义一个函数来计算卷积层。它对输入和输出做相应的升维和降维
def comp_conv2d(conv2d, X):
    # (1, 1)代表批量大小和通道数
    X = X.view((1, 1) + X.shape)
    Y = conv2d(X)
    return Y.view(Y.shape[2:]) # 排除不关心的前两维:批量和通道


# 注意这里是两侧分别填充1⾏或列，所以在两侧一共填充2⾏或列
conv2d = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3,padding=1)

X = torch.rand(8, 8)
comp_conv2d(conv2d, X).shape

torch.Size([8, 8])

在二维互相关运算中，卷积窗口从输入数组的最左上方开始，按从左往右、从上往下的顺序，依次在输入数组上滑动。我们将每次滑动的行数和列数称为步幅(stride)。

conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))
comp_conv2d(conv2d, X).shape

torch.Size([2, 2])

---

代码解析：

1. torch.view对张量进行重塑；

   X = torch.randn(3,3)
   X = X.view((1,1)+X.shape)
   print(X.shape)
   print(X)
   
   torch.Size([1, 1, 3, 3])
   tensor([[[[ 1.2421, -1.3165, -1.0270],
             [-0.1203, -0.3010, -0.2302],
             [ 0.0266,  0.7969, -0.7544]]]])
   

2. nn.Conv2d构建了一个卷积层，comp_con2d输入卷积层与数据，首先对输入数据X进行升维，增加批量大小和通道维度，然后通过conv2d(X)将X输入至卷积层中，然后对输出进行降维剔除批量和通道信息。
   conv2d的输入为x[ batch_size, channels, height_1, width_1 ]其中前两项分别为批量大小和通道数。因此需要对输入输出分别进行升维降维处理。

---

• 池化层
  又称作下采样，其基本原理是根据图像相对不变性的属性，对图像相邻区域的特征信息进行聚合统计，实现降维。常用的方法有，最大池化法、均值池化法、高斯池化法和可训练池化法。
  池化的主要作用是：
  1. 降低图像分辨率；
  2. 减少运算数据量；
  3. 增强网络对图像变化的适应性。

下面把池化层的前向计算实现在pol2d函数里。

import torch
from torch import nn

def pool2d(X, pool_size, mode='max'):
    p_h, p_w = pool_size
    Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode == 'max':
                Y[i, j] = X[i: i + p_h, j: j + p_w].max()
            elif mode == 'avg':
                Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
    return Y

X = torch.tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]], dtype=torch.float)
pool2d(X, (2, 2))

# result
tensor([[4., 5.],
		[7., 8.]])

我们可以使用torch.nn包来构建神经网络。nn包则依赖于autograd包来定义模型并对它们求导。一个nn.Module包含各个层和一个forward(input)方法，该方法返回output。

---

代码解析：
代码中需要注意的是在张量中通过切片提取最大值或平均值简化了代码。

Y[i, j] = X[i: i + p_h, j: j + p_w].max()
Y[i, j] = X[i: i + p_h, j: j + p_w].mean()

---

1.4.3 模型示例

• LeNet

是一个简单的前馈神经网络(feed-forward network)。常用于手写字符识别，LeNet接受一个输入，然后将它送入下一层，一层接一层传递，最后输出。
一个神经网络典型训练过程如下：

1. 定义包含一些可学习参数(权重)的神经网络；
2. 在输入数据集上迭代；
3. 通过网络处理输入；
4. 计算loss；
5. 将梯度反向传播给网格的参数；
6. 更新网络的权重，常用简单规则：weight = weight - learning_rate + gradient。

import torch
import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 输入图像channel：1；输出channel：6；5x5卷积核
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # 2x2 Max pooling
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # 如果是方阵,则可以只使用一个数字进行定义
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        size = x.size()[1:]  # 除去批处理维度的其他所有维度
        num_features = 1
        for s in size:
            num_features *= s
        return num_features


net = Net()
print(net)

# result
Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

我们只需要定义forward函数，backward函数会在使用autograd时自动定义，backward函数用来计算导数。我们可以在forward函数中使用任何针对张量的操作和计算。
一个模型的可学习参数可以通过net.parameters()返回：

params = list(net.parameters())
print(len(params))
print(params[0].size())  # conv1的权重

# result
10
torch.Size([6, 1, 5, 5])

让我们尝试一个随机的 32x32 的输入。注意:这个网络 (LeNet）的期待输入是 32x32 的张量。如果使用 MNIST 数据集来训练这个网络，要把图片大小重新调整到 32x32。

input = torch.randn(1, 1, 32, 32)
out = net(input)
print(out)

清零所有参数的梯度缓存，然后进行随机梯度的反向传播：

net.zero_grad()
out.backward(torch.randn(1, 10))

注意：torch.nn只支持小批量处理 (mini-batches）。整个 torch.nn 包只支持小批量样本的输入，不支持单个样本的输入。比如，nn.Conv2d 接受一个4维的张量，即nSamples x nChannels x Height x Width 如果是一个单独的样本，只需要使用input.unsqueeze(0) 来添加一个“假的”批大小维度。

• torch.Tensor - 一个多维数组，支持诸如backward()等的自动求导操作，同时也保存了张量的梯度；
• nn.Module - 神经网络模块。是一种方便封装参数的方式，具有将参数移动到GPU、导出、加载等功能；
• nn.Parameter - 张量的一种，当它作为一个属性分配给一个Module时，它会被自动注册为一个参数；
• autograd.Function - 实现了自动求导前向和反向传播的定义，每个Tensor至少创建一个Function节点，该节点连接到创建Tensor的函数并对其历史进行编码。

---

代码解析：

1. nn.Conv2d[ channels, output, height_2, width_2 ]参数分别为输入、输出通道数和卷积核的高和宽，如果是方阵则可以用一个数字代替。nn.Linear输入的参数同样分别为输入神经元个数和输出神经元个数。
2. LeNet中前向计算步骤：卷积计算–最大值池化–卷积计算–最大值池化–通过ReLu激活函数搭建的三层全连接层–输出。
3. x=x.view(-1, self.num_flat_features(x))其中-1表示由第二个输入的数字决定该位置的维度。这里为什么要使用[1:],是因为pytorch只接受批输入，也就是说一次性输入好几张图片，因此输入数据的第一维总是批处理维度。num_flat_features用于计算出批处理维度之外的所有维度。
4. 一个模型的可学习参数可以通过net.parameters()返回，在前向传播中如果需要自己定义一个带参数的层，通过nn.Parameter()创建的参数会自动添加到模型的参数信息中同其他层的参数一起，如果不想进行优化则可在创建参数的函数中进行选择。

---

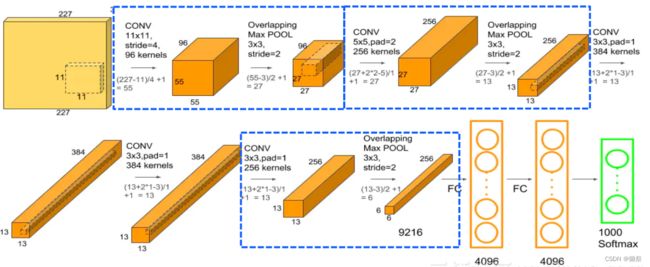
下面介绍AlexNet

• AlexNet
  AlexNet是2012年ImageNet比赛的冠军。主要创新点有：ReLU、LRN、Dropout。
  

class AlexNet(nn.Module):
    def __init__(self):
        super(AlexNet, self).__init__()
        self.conv = nn.Sequential(
            nn.Conv2d(1, 96, 11, 4), # in_channels, out_channels, kernel_size, stride, padding
            nn.ReLU(),
            nn.MaxPool2d(3, 2), # kernel_size, stride
            # 减小卷积窗口，使用填充为2来使得输入与输出的高和宽一致，且增大输出通道数
            nn.Conv2d(96, 256, 5, 1, 2),
            nn.ReLU(),
            nn.MaxPool2d(3, 2),
            # 连续3个卷积层，且使用更小的卷积窗口。除了最后的卷积层外，进一步增大了输出通道数。
            # 前两个卷积层后不使用池化层来减小输入的高和宽
            nn.Conv2d(256, 384, 3, 1, 1),
            nn.ReLU(),
            nn.Conv2d(384, 384, 3, 1, 1),
            nn.ReLU(),
            nn.Conv2d(384, 256, 3, 1, 1),
            nn.ReLU(),
            nn.MaxPool2d(3, 2)
        )
         # 这里全连接层的输出个数比LeNet中的大数倍。使用丢弃层来缓解过拟合
        self.fc = nn.Sequential(
            nn.Linear(256*5*5, 4096),
            nn.ReLU(),
            nn.Dropout(0.5),
            nn.Linear(4096, 4096),
            nn.ReLU(),
            nn.Dropout(0.5),
            # 输出层。由于这里使用Fashion-MNIST，所以用类别数为10，而非论文中的1000
            nn.Linear(4096, 10),
        )

    def forward(self, img):
        feature = self.conv(img)
        output = self.fc(feature.view(img.shape[0], -1))
        return output

# run
net = AlexNet()
print(net)

# result
AlexNet(
  (conv): Sequential(
    (0): Conv2d(1, 96, kernel_size=(11, 11), stride=(4, 4))
    (1): ReLU()
    (2): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
    (3): Conv2d(96, 256, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
    (4): ReLU()
    (5): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
    (6): Conv2d(256, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (7): ReLU()
    (8): Conv2d(384, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (9): ReLU()
    (10): Conv2d(384, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (11): ReLU()
    (12): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (fc): Sequential(
    (0): Linear(in_features=6400, out_features=4096, bias=True)
    (1): ReLU()
    (2): Dropout(p=0.5)
    (3): Linear(in_features=4096, out_features=4096, bias=True)
    (4): ReLU()
    (5): Dropout(p=0.5)
    (6): Linear(in_features=4096, out_features=10, bias=True)
  )
)

---

代码解析：
AlexNet利用nn.Sequential以串联的方式定义了网络结构，其中conv为卷积部分，fc为全连接层部分。需要注意的是调用ReLu函数的方式和前面的部分有区别。

---

1.5 模型初始化

深度学习本质上就是对网络参数的优化算法，因此在目标函数非凸的情况下，迭代初始值的选取十分重要。

1.5.1 torch.nn.init常用方法

torch.nn.init文档官方链接

1. torch.nn.init.uniform(tensor, a=0, b=1) 从均匀分布U(a,b)中生成值，填充输入的张量或变量；
2. torch.nn.init.normal(tensor, mean=0, std=1)从给定均值和标准差的正态分布N(mean, std)中生成值，填充输入的张量或变量；
3. torch.nn.init.constant(tensor, val)用val的值填充输入的张量或变量；
4. torch.nn.init.eye(tensor)用单位矩阵来填充2维输入张量或变量。在线性层尽可能多的保存输入特性；
5. torch.nn.init.dirac(tensor)用Dirac $\delta$ 函数来填充{3, 4, 5}维输入张量或变量。在卷积层尽可能多的保存输入通道特性；
6. torch.nn.init.xavier_uniform(tensor, gain=1)根据Glorot, X.和Bengio, Y.在“Understanding the difficulty of training deep feedforward neural networks”中描述的方法，用一个均匀分布生成值，填充输入的张量或变量。结果张量中的值采样自U(-a, a)，其中$a=gain\ast \sqrt{2/(fa{n}_{i}n+fa{n}_{o}ut)}\ast \sqrt{3}$. 该方法也被称为Glorot initialisation。

1.5.2 torch.nn.init使用

我们通常会根据实际模型来使用torch.nn.init进行初始化，通常使用isinstance来进行判断模块（回顾1.4模型构建）属于什么类型。

import torch
import torch.nn as nn

conv = nn.Conv2d(1,3,3)
linear = nn.Linear(10,1)

isinstance(conv,nn.Conv2d)
isinstance(linear,nn.Conv2d)

# result
True
False

对于不同的类型层，我们就可以设置不同的权值初始化的方法。

# 查看随机初始化的conv参数
conv.weight.data
# 查看linear的参数
linear.weight.data

# results
tensor([[[[ 0.1174,  0.1071,  0.2977],
          [-0.2634, -0.0583, -0.2465],
          [ 0.1726, -0.0452, -0.2354]]],
        [[[ 0.1382,  0.1853, -0.1515],
          [ 0.0561,  0.2798, -0.2488],
          [-0.1288,  0.0031,  0.2826]]],
        [[[ 0.2655,  0.2566, -0.1276],
          [ 0.1905, -0.1308,  0.2933],
          [ 0.0557, -0.1880,  0.0669]]]])

tensor([[-0.0089,  0.1186,  0.1213, -0.2569,  0.1381,  0.3125,  0.1118, -0.0063, -0.2330,  0.1956]])

# 对conv进行kaiming初始化
torch.nn.init.kaiming_normal_(conv.weight.data)
conv.weight.data
# 对linear进行常数初始化
torch.nn.init.constant_(linear.weight.data,0.3)
linear.weight.data

# results
tensor([[[[ 0.3249, -0.0500,  0.6703],
          [-0.3561,  0.0946,  0.4380],
          [-0.9426,  0.9116,  0.4374]]],
        [[[ 0.6727,  0.9885,  0.1635],
          [ 0.7218, -1.2841, -0.2970],
          [-0.9128, -0.1134, -0.3846]]],
        [[[ 0.2018,  0.4668, -0.0937],
          [-0.2701, -0.3073,  0.6686],
          [-0.3269, -0.0094,  0.3246]]]])
tensor([[0.3000, 0.3000, 0.3000, 0.3000, 0.3000, 0.3000, 0.3000, 0.3000, 0.3000,0.3000]])

1.5.3 初始化函数的封装

人们常常将初始化方法定义为initialize_weights()的函数并在模型初始后使用。

def initialize_weights(self):
	for m in self.modules():
		# 判断是否属于Conv2d
		if isinstance(m, nn.Conv2d):
			torch.nn.init.xavier_normal_(m.weight.data)
			# 判断是否有偏置
			if m.bias is not None:
				torch.nn.init.constant_(m.bias.data,0.3)
		elif isinstance(m, nn.Linear):
			torch.nn.init.normal_(m.weight.data, 0.1)
			if m.bias is not None:
				torch.nn.init.zeros_(m.bias.data)
		elif isinstance(m, nn.BatchNorm2d):
			m.weight.data.fill_(1) 		 
			m.bias.data.zeros_()	

代码逻辑为遍历当前每一层，并判断分别属于什么类型，然后根据不同类型设定不同初始化方法。

# 模型的定义
class MLP(nn.Module):
  # 声明带有模型参数的层，这里声明了两个全连接层
  def __init__(self, **kwargs):
    # 调用MLP父类Block的构造函数来进行必要的初始化。这样在构造实例时还可以指定其他函数
    super(MLP, self).__init__(**kwargs)
    self.hidden = nn.Conv2d(1,1,3)
    self.act = nn.ReLU()
    self.output = nn.Linear(10,1)
    
   # 定义模型的前向计算，即如何根据输入x计算返回所需要的模型输出
  def forward(self, x):
    o = self.act(self.hidden(x))
    return self.output(o)

mlp = MLP()
print(list(mlp.parameters()))
print("-------初始化-------")

initialize_weights(mlp)
print(list(mlp.parameters()))

# results
[Parameter containing:
tensor([[[[ 0.2103, -0.1679,  0.1757],
          [-0.0647, -0.0136, -0.0410],
          [ 0.1371, -0.1738, -0.0850]]]], requires_grad=True), Parameter containing:
tensor([0.2507], requires_grad=True), Parameter containing:
tensor([[ 0.2790, -0.1247,  0.2762,  0.1149, -0.2121, -0.3022, -0.1859,  0.2983,
         -0.0757, -0.2868]], requires_grad=True), Parameter containing:
tensor([-0.0905], requires_grad=True)]
"-------初始化-------"
[Parameter containing:
 tensor([[[[-0.3196, -0.0204, -0.5784],
           [ 0.2660,  0.2242, -0.4198],
           [-0.0952,  0.6033, -0.8108]]]], requires_grad=True),
 Parameter containing:
 tensor([0.3000], requires_grad=True),
 Parameter containing:
 tensor([[ 0.7542,  0.5796,  2.2963, -0.1814, -0.9627,  1.9044,  0.4763,  1.2077,
           0.8583,  1.9494]], requires_grad=True),
 Parameter containing:
 tensor([0.], requires_grad=True)]

---

代码解析：
初始化部分的代码较为简单，但初始化调参在训练过程中也是非常重要的一步。上面的代码中需要注意的是initialize_weights并没有定义在类中，而是单独定义，但是也可以定义在类中结果一样。initialize_weights中for m in self.modules()的self.modules()由于继承了父类，因此具有这个属性，在定义了各个层并用forward()连接之后，便自动具有这个属性。

---

1.6 损失函数

损失函数即为优化过程中所使用到的目标函数，对于不同的输出结果所需要的损失函数也不同，常用的损失函数如下：

1.6.0 基本用法

损失函数的基本调用方式

# 实例化损失函数，构造函数有自己的参数
criterion = LossCriterion()
# 使用损失函数时，也需要特定的输入输出格式
loss = criterion(x, y)

参考文献：
Pytorch损失函数

1.6.1 二分类交叉熵损失函数

torch.nn.BCELoss(weight=None, size_average=None, reduce=None, reduction='mean')

功能： 计算二分类任务时的交叉熵（Cross Entropy）函数。在二分类中，label是{0,1}。对于进入交叉熵函数的input为概率分布的形式。一般来说，input为sigmoid激活层的输出，或者softmax函数的输出。
交叉熵与softmax的定义在链接中写的十分详细。

---

交叉熵介绍思路：
最佳编码及编码成本——>代价与概率正比关系——>熵的定义——>提出问题：概率分布与最佳编码不同时——>提出交叉熵概念与KL散度概念——>利用极大似然法推导出交叉熵作为损失函数的用法。

---

主要参数：
weight：每个类别的loss设置的权值；
size_average：数据为bool，为True时，返回的loss为平均值；为False时，返回的各样本的loss之和；
reduce：数据类型为bool，为True时，loss的返回是标量。
计算公式：
$$\begin{gathered} l(x,y)=\{\begin{array}{cc}mean(L),& ifreduction{=}^{\prime }mea{n}^{\prime }\\ sum(L),& ifreduction{=}^{\prime }su{m}^{\prime }\end{array} \\ {L}_i(\theta )=y_{i}log\theta +(1-y_i)log(1-\theta ) \end{gathered}$$
调用：

m = nn.Sigmoid()
loss = nn.BCELoss()
input = torch.randn(3, requires_grad=True)
target = torch.empty(3).random_(2)
output = loss(m(input), target)
output.backward()

# run
print('BCELoss损失函数的计算结果为',output)

# result
BCELoss损失函数的计算结果为 tensor(0.5732, grad_fn=<BinaryCrossEntropyBackward>)

1.6.2 交叉熵损失函数

torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')

功能： 计算多分类问题中的交叉熵损失函数。
主要参数：
weight：每个类别的loss设置权值；
size_average：数据为bool，为True时，返回的loss为平均值；为False时，返回的各样本的loss之和；
ignore_index：忽略某个类的损失函数；
reduce：数据类型为bool，为True时，loss的返回是标量。
计算公式：
$$\begin{gathered} loss(x,class)=-log(\frac{exp(x[class])}{{\sum }_{j}exp(x[j])} \\ =-x[class]+log(\sum _{j}exp(x[j]) \end{gathered}$$
调用：

loss = nn.CrossEntropyLoss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.empty(3, dtype=torch.long).random_(5)
output = loss(input, target)
output.backward()

# run
print(output)

#result
tensor(2.0115, grad_fn=<NllLossBackward>)

1.6.3 L1损失函数

torch.nn.L1Loss(size_average=None, reduce=None, reduction='mean')

功能： 以L1范数作为损失函数，计算输出y和真实标签target之间的绝对值；
主要参数：
reduction：reduction参数决定了计算模式。有三种计算模式可选：none：逐个元素计算。 sum：所有元素求和，返回标量。 mean：加权平均，返回标量。 如果选择none，那么返回的结果是和输入元素相同尺寸的。默认计算方式是求平均。
计算公式：
$$L_n=|x_n-y_n|$$
调用：

loss = nn.L1Loss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
output = loss(input, target)
output.backward()

# run
print('L1损失函数的计算结果为',output)

# result
L1损失函数的计算结果为 tensor(1.5729, grad_fn=<L1LossBackward>)

1.6.4 MSE损失函数

torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean')

功能： 比较常用的函数，利用L2范数计算损失值；
主要参数： reduction：reduction参数决定了计算模式。有三种计算模式可选：none：逐个元素计算。 sum：所有元素求和，返回标量。 mean：加权平均，返回标量。 如果选择none，那么返回的结果是和输入元素相同尺寸的。默认计算方式是求平均。
计算公式：
$$L_n=(x_n-y_n{)}^2$$

loss = nn.MSELoss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
output = loss(input, target)
output.backward()

# run
print('MSE损失函数的计算结果为',output)
# result
MSE损失函数的计算结果为 tensor(1.6968, grad_fn=<MseLossBackward>)

1.6.5 平滑L1损失函数

torch.nn.SmoothL1Loss(size_average=None, reduce=None, reduction='mean', beta=1.0)

功能： 相较L1损失函数，在原点附近添加一段二次函数作平滑过渡；
计算公式：
$$\begin{gathered} loss(x,y)=\frac{1}{n}\sum _{i=1}^n{z}_i \\ 程序=\{\begin{array}{cc}0.5(x_i-y_i{)}^2,& if|x_i-y_i|<1\\ |x_i-y_i|-0.5,& otherwise\end{array} \end{gathered}$$

loss = nn.SmoothL1Loss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
output = loss(input, target)
output.backward()

# run
print('SmoothL1Loss损失函数的计算结果为',output)

# result
SmoothL1Loss损失函数的计算结果为 tensor(0.7808, grad_fn=<SmoothL1LossBackward>)

1.6.6 目标泊松分布的负对数似然损失

torch.nn.PoissonNLLLoss(log_input=True, full=False, size_average=None, eps=1e-08, reduce=None, reduction='mean')

**功能：**泊松分布的负对数似然函数
主要参数：
log_input：输入是否为对数形式，决定计算公式；
full：计算所有 loss，默认为 False；
eps：修正项，避免 input 为 0 时，log(input) 为 nan 的情况。
数学公式：
$$loss(x_n,y_n)=\{\begin{array}{cc}{e}^{x_n}-x_n{y}_n,& iflo{g}_{i}nput=True\\ x_n-y_{n}log(x_n+eps)& iflo{g}_{i}nput=False\end{array}$$
调用：

loss = nn.PoissonNLLLoss()
log_input = torch.randn(5, 2, requires_grad=True)
target = torch.randn(5, 2)
output = loss(log_input, target)
output.backward()

# run
print('PoissonNLLLoss损失函数的计算结果为',output)

# result
PoissonNLLLoss损失函数的计算结果为 tensor(0.7358, grad_fn=<MeanBackward0>)

1.6.7 KL散度

torch.nn.KLDivLoss(size_average=None, reduce=None, reduction='mean', log_target=False)

功能： 计算KL散度，也就是计算相对熵。用于连续分布的距离度量，并且对离散采用的连续输出空间分布进行回归通常很有用。KL散度可用于衡量不同的连续分布之间的距离, 在连续的输出分布的空间上(离散采样)上进行直接回归时很有效。
主要参数：
reduction参数多了一个计算模式：
batchmean：batchsize维度求平均值；
计算公式：
$$\begin{gathered} D_{KL}(P,Q)=E_{X-P}[log\frac{P(X)}{Q(X)}] \\ =E_{X-P}[logP(X)-logQ(X)] \\ =\sum _{i=1}^{n}P(x_i)(logP(x_i)-logQ(x_i)) \end{gathered}$$

inputs = torch.tensor([[0.5, 0.3, 0.2], [0.2, 0.3, 0.5]])
target = torch.tensor([[0.9, 0.05, 0.05], [0.1, 0.7, 0.2]], dtype=torch.float)
loss = nn.KLDivLoss()
output = loss(inputs,target)

print('KLDivLoss损失函数的计算结果为',output)

KLDivLoss损失函数的计算结果为 tensor(-0.3335)

1.6.8 MarginRankingLoss

torch.nn.MarginRankingLoss(margin=0.0, size_average=None, reduce=None, reduction='mean')

功能： 计算两个向量之间的相似度，用于排序任务。该方法用于计算两组数据之间的差异；
主要参数：
margin：边界值，$x_1$与$x_2$之间的差异值；
计算公式：
$$loss(x_1,x_2,y)=\max 0,-y\ast (x_1-x_2)+margin$$

loss = nn.MarginRankingLoss()
input1 = torch.randn(3, requires_grad=True)
input2 = torch.randn(3, requires_grad=True)
target = torch.randn(3).sign()
output = loss(input1, input2, target)
output.backward()

print('MarginRankingLoss损失函数的计算结果为',output)

MarginRankingLoss损失函数的计算结果为 tensor(0.7740, grad_fn=<MeanBackward0>)

1.6.9 多标签边界损失函数

torch.nn.MultiLabelMarginLoss(size_average=None, reduce=None, reduction='mean')

功能： 对于多标签分类问题计算损失函数；
计算公式：
$$loss(x,y)=\sum _{ij}\frac{\max (0,1-x[y[j]]-x[i]}{x\cdot size(0)}$$
其中，$i=0,...,x\cdot size(0),j=0,...,y\cdot size(0)$，对于所有$i$和$j$，都有$y[j]>=0$且$i\ne y[j]$

loss = nn.MultiLabelMarginLoss()
x = torch.FloatTensor([[0.9, 0.2, 0.4, 0.8]])
# for target y, only consider labels 3 and 0, not after label -1
y = torch.LongTensor([[3, 0, -1, 1]])# 真实的分类是，第3类和第0类
output = loss(x, y)

print('MultiLabelMarginLoss损失函数的计算结果为',output)

MultiLabelMarginLoss损失函数的计算结果为 tensor(0.4500)

1.6.10 二分类损失函数

torch.nn.SoftMarginLoss(size_average=None, reduce=None, reduction='mean')

功能：
计算公式：
$$loss(x,y)=\sum _i\frac{log(1+exp(-y[i]\cdot x[i]))}{x\cdot nelement()}$$
其中$x\cdot nelement$为输入x中样本个数，这里y也有1，-1两种值。

inputs = torch.tensor([[0.3, 0.7], [0.5, 0.5]])  # 两个样本，两个神经元
target = torch.tensor([[-1, 1], [1, -1]], dtype=torch.float)  # 该 loss 为逐个神经元计算，需要为每个神经元单独设置标签

loss_f = nn.SoftMarginLoss()
output = loss_f(inputs, target)

print('SoftMarginLoss损失函数的计算结果为',output)

SoftMarginLoss损失函数的计算结果为 tensor(0.6764)

1.6.11 多分类的折页损失

torch.nn.MultiMarginLoss(p=1, margin=1.0, weight=None, size_average=None, reduce=None, reduction='mean')

功能： 多分类问题的折页损失
主要参数：
p：可选1，2；
weight：各类别loss设置权值；
margin边界值。
计算公式：
$$loss(x,y)=\frac{{\sum }_i\max (0,margin-x[y]+x[i]}{x\cdot size(0)}$$
其中，$x\in 0,...,x\cdot size(0)-1$，$y\in 0,...,y\cdot size(0)-1$且对于所有$i$，$j$，有$0<=y[j]<=x\cdot size(0)-1,i\ne y[j]$

inputs = torch.tensor([[0.3, 0.7], [0.5, 0.5]]) 
target = torch.tensor([0, 1], dtype=torch.long) 

loss_f = nn.MultiMarginLoss()
output = loss_f(inputs, target)

print('MultiMarginLoss损失函数的计算结果为',output)

MultiMarginLoss损失函数的计算结果为 tensor(0.6000)

1.6.12 三元组损失

torch.nn.TripletMarginLoss(margin=1.0, p=2.0, eps=1e-06, swap=False, size_average=None, reduce=None, reduction='mean')

功能：
三元组： 这是一种数据的存储或者使用格式。<实体1，关系，实体2>。在项目中，也可以表示为< anchor, positive examples , negative examples>

在这个损失函数中，我们希望去anchor的距离更接近positive examples，而远离negative examples
主要参数： 同1.6.11
计算公式：
$$\begin{gathered} L(a,p,n)=\max \{d(a_i,p_i)-d(a_i,n_i)+margin,0\} \\ d(x,y)=||x_i-y_i|| \end{gathered}$$

triplet_loss = nn.TripletMarginLoss(margin=1.0, p=2)
anchor = torch.randn(100, 128, requires_grad=True)
positive = torch.randn(100, 128, requires_grad=True)
negative = torch.randn(100, 128, requires_grad=True)
output = triplet_loss(anchor, positive, negative)
output.backward()
print('TripletMarginLoss损失函数的计算结果为',output)

TripletMarginLoss损失函数的计算结果为 tensor(1.1667, grad_fn=<MeanBackward0>)

1.6.13 HingEmbeddingLoss

torch.nn.HingeEmbeddingLoss(margin=1.0, size_average=None, reduce=None, reduction='mean')

功能： 对输出的embedding结果做Hing损失计算
主要参数：
计算公式：
$$l_n=\{\begin{array}{cc}{x}_n,& if{y}_n=1\\ \max \{0,△-x_n\}& if{y}_n=-1\end{array}$$
输入x应为两个输入之差的绝对值。

loss_f = nn.HingeEmbeddingLoss()
inputs = torch.tensor([[1., 0.8, 0.5]])
target = torch.tensor([[1, 1, -1]])
output = loss_f(inputs,target)

print('HingEmbeddingLoss损失函数的计算结果为',output)

HingEmbeddingLoss损失函数的计算结果为 tensor(0.7667)

1.6.14 余弦相似度

torch.nn.CosineEmbeddingLoss(margin=0.0, size_average=None, reduce=None, reduction='mean')

功能： 对两个向量做余弦相似度
主要参数：
计算公式：
$$\begin{gathered} \mathrm{loss}(x,y)=\{\begin{array}{ll}1-\cos \left(x_1,x_2\right),& \text{ if }y=1\\ \max \left\{0,\cos \left(x_1,x_2\right)-\mathrm{margin}\right\},& \text{ if }y=-1\end{array} \\ \begin{array}{c}\cos (\theta )=\frac{A\cdot B}{\Vert A\Vert \Vert B\Vert }=\frac{{\sum }_{i=1}^n{A}_i\times B_i}{\sqrt{{\sum }_{i=1}^n{\left(A_i\right)}^2}\times \sqrt{{\sum }_{i=1}^n{\left(B_i\right)}^2}}\end{array} \end{gathered}$$

loss_f = nn.CosineEmbeddingLoss()
inputs_1 = torch.tensor([[0.3, 0.5, 0.7], [0.3, 0.5, 0.7]])
inputs_2 = torch.tensor([[0.1, 0.3, 0.5], [0.1, 0.3, 0.5]])
target = torch.tensor([[1, -1]], dtype=torch.float)
output = loss_f(inputs_1,inputs_2,target)

print('CosineEmbeddingLoss损失函数的计算结果为',output)

CosineEmbeddingLoss损失函数的计算结果为 tensor(0.5000)

1.6.15 CTC损失函数

torch.nn.CTCLoss(blank=0, reduction='mean', zero_infinity=False)

功能： 用于解决时序类数据的分类
计算连续时间序列和目标序列之间的损失。CTCLoss对输入和目标的可能排列的概率进行求和，产生一个损失值，这个损失值对每个输入节点来说是可分的。输入与目标的对齐方式被假定为 “多对一”，这就限制了目标序列的长度，使其必须是≤输入长度。
主要参数：
blank：空白标签；
zero_infinity：无穷大的值或梯度值

# Target are to be padded
T = 50      # Input sequence length
C = 20      # Number of classes (including blank)
N = 16      # Batch size
S = 30      # Target sequence length of longest target in batch (padding length)
S_min = 10  # Minimum target length, for demonstration purposes

# Initialize random batch of input vectors, for *size = (T,N,C)
input = torch.randn(T, N, C).log_softmax(2).detach().requires_grad_()

# Initialize random batch of targets (0 = blank, 1:C = classes)
target = torch.randint(low=1, high=C, size=(N, S), dtype=torch.long)

input_lengths = torch.full(size=(N,), fill_value=T, dtype=torch.long)
target_lengths = torch.randint(low=S_min, high=S, size=(N,), dtype=torch.long)
ctc_loss = nn.CTCLoss()
loss = ctc_loss(input, target, input_lengths, target_lengths)
loss.backward()


# Target are to be un-padded
T = 50      # Input sequence length
C = 20      # Number of classes (including blank)
N = 16      # Batch size

# Initialize random batch of input vectors, for *size = (T,N,C)
input = torch.randn(T, N, C).log_softmax(2).detach().requires_grad_()
input_lengths = torch.full(size=(N,), fill_value=T, dtype=torch.long)

# Initialize random batch of targets (0 = blank, 1:C = classes)
target_lengths = torch.randint(low=1, high=T, size=(N,), dtype=torch.long)
target = torch.randint(low=1, high=C, size=(sum(target_lengths),), dtype=torch.long)
ctc_loss = nn.CTCLoss()
loss = ctc_loss(input, target, input_lengths, target_lengths)
loss.backward()

print('CTCLoss损失函数的计算结果为',loss)

CTCLoss损失函数的计算结果为 tensor(16.0885, grad_fn=<MeanBackward0>)

1.7 训练与评估

模型有两种可设置状态：
训练状态： 模型参数支持反向传播的修改；
测试状态： 利用已有参数对数据进行验证。
完整的训练步骤：

1. 设定模型状态；
2. 利用for循环读取DataLoader中所有数据；
3. 将数据放到GPU上进行计算；
4. 开始用当前批次数据做训练时，先将优化器梯度置零；
5. 将data送入模型中训练；
6. 根据预先定义的criterion计算损失函数；
7. 将loss反向传播回网络；
8. 使用优化器更新模型参数；

验证/测试流程基本一致，不同之处在于：

• 需要预先设置torch.no_grad，以及将model调至eval模式
• 不需要将优化器的梯度置零
• 不需要将loss反向回传到网络
• 不需要更新optimizer
  完整训练代码：

def train(epoch):
    model.train()
    train_loss = 0
    for data, label in train_loader:
        data, label = data.cuda(), label.cuda()
        optimizer.zero_grad()
        output = model(data)
        loss = criterion(label, output)
        loss.backward()
        optimizer.step()
        train_loss += loss.item()*data.size(0)
    train_loss = train_loss/len(train_loader.dataset)
		print('Epoch: {} \tTraining Loss: {:.6f}'.format(epoch, train_loss))

完整验证代码：

def val(epoch):       
    model.eval()
    val_loss = 0
    with torch.no_grad():
        for data, label in val_loader:
            data, label = data.cuda(), label.cuda()
            output = model(data)
            preds = torch.argmax(output, 1)
            loss = criterion(output, label)
            val_loss += loss.item()*data.size(0)
            running_accu += torch.sum(preds == label.data)
    val_loss = val_loss/len(val_loader.dataset)
    print('Epoch: {} \tTraining Loss: {:.6f}'.format(epoch, val_loss))

---

代码解析：
loss.item()取loss的高精度值，data.size(0)取data第0维的数据个数

---

1.8 可视化

TODO

1.9 优化器

优化器是根据网络反向传播的梯度信息来更新网络的参数，以起到降低loss函数计算值，使得模型输出更加接近真实标签。

1.9.1 Pytorch官方优化器

Pytorch官方提供了一个优化器的库torch.optim，在这里面提供了始终优化器，均继承于Optimizer。所有优化器的基类Optimizer定义如下：

class Optimizer(object):
    def __init__(self, params, defaults):        
        self.defaults = defaults
        self.state = defaultdict(dict)
        self.param_groups = []
        
    def zero_grad(self, set_to_none: bool = False):
	    for group in self.param_groups:
	        for p in group['params']:
	            if p.grad is not None:  #梯度不为空
	                if set_to_none: 
	                    p.grad = None
	                else:
	                    if p.grad.grad_fn is not None:
	                        p.grad.detach_()
	                    else:
	                        p.grad.requires_grad_(False)
	                    p.grad.zero_()# 梯度设置为0
	def step(self, closure): 
	    raise NotImplementedError
	
	def add_param_group(self, param_group):
    assert isinstance(param_group, dict), "param group must be a dict"
# 检查类型是否为tensor
    params = param_group['params']
    if isinstance(params, torch.Tensor):
        param_group['params'] = [params]
    elif isinstance(params, set):
        raise TypeError('optimizer parameters need to be organized in ordered collections, but '
                        'the ordering of tensors in sets will change between runs. Please use a list instead.')
    else:
        param_group['params'] = list(params)
    for param in param_group['params']:
        if not isinstance(param, torch.Tensor):
            raise TypeError("optimizer can only optimize Tensors, "
                            "but one of the params is " + torch.typename(param))
        if not param.is_leaf:
            raise ValueError("can't optimize a non-leaf Tensor")

    for name, default in self.defaults.items():
        if default is required and name not in param_group:
            raise ValueError("parameter group didn't specify a value of required optimization parameter " +
                             name)
        else:
            param_group.setdefault(name, default)

    params = param_group['params']
    if len(params) != len(set(params)):
        warnings.warn("optimizer contains a parameter group with duplicate parameters; "
                      "in future, this will cause an error; "
                      "see github.com/pytorch/pytorch/issues/40967 for more information", stacklevel=3)
# 上面好像都在进行一些类的检测，报Warning和Error
    param_set = set()
    for group in self.param_groups:
        param_set.update(set(group['params']))

    if not param_set.isdisjoint(set(param_group['params'])):
        raise ValueError("some parameters appear in more than one parameter group")
# 添加参数
    self.param_groups.append(param_group)

	def load_state_dict(self, state_dict):
    r"""Loads the optimizer state.

    Arguments:
        state_dict (dict): optimizer state. Should be an object returned
            from a call to :meth:`state_dict`.
    """
    # deepcopy, to be consistent with module API
    state_dict = deepcopy(state_dict)
    # Validate the state_dict
    groups = self.param_groups
    saved_groups = state_dict['param_groups']

    if len(groups) != len(saved_groups):
        raise ValueError("loaded state dict has a different number of "
                         "parameter groups")
    param_lens = (len(g['params']) for g in groups)
    saved_lens = (len(g['params']) for g in saved_groups)
    if any(p_len != s_len for p_len, s_len in zip(param_lens, saved_lens)):
        raise ValueError("loaded state dict contains a parameter group "
                         "that doesn't match the size of optimizer's group")

    # Update the state
    id_map = {old_id: p for old_id, p in
              zip(chain.from_iterable((g['params'] for g in saved_groups)),
                  chain.from_iterable((g['params'] for g in groups)))}

    def cast(param, value):
        r"""Make a deep copy of value, casting all tensors to device of param."""
   		.....

    # Copy state assigned to params (and cast tensors to appropriate types).
    # State that is not assigned to params is copied as is (needed for
    # backward compatibility).
    state = defaultdict(dict)
    for k, v in state_dict['state'].items():
        if k in id_map:
            param = id_map[k]
            state[param] = cast(param, v)
        else:
            state[k] = v

    # Update parameter groups, setting their 'params' value
    def update_group(group, new_group):
       ...
    param_groups = [
        update_group(g, ng) for g, ng in zip(groups, saved_groups)]
    self.__setstate__({'state': state, 'param_groups': param_groups})

def state_dict(self):
    r"""Returns the state of the optimizer as a :class:`dict`.

    It contains two entries:

    * state - a dict holding current optimization state. Its content
        differs between optimizer classes.
    * param_groups - a dict containing all parameter groups
    """
    # Save order indices instead of Tensors
    param_mappings = {}
    start_index = 0

    def pack_group(group):
		......
    param_groups = [pack_group(g) for g in self.param_groups]
    # Remap state to use order indices as keys
    packed_state = {(param_mappings[id(k)] if isinstance(k, torch.Tensor) else k): v
                    for k, v in self.state.items()}
    return {
        'state': packed_state,
        'param_groups': param_groups,
    }

1.9.2 实际操作

import os
import torch

# 设置权重，服从正态分布  --> 2 x 2
weight = torch.randn((2, 2), requires_grad=True)
# 设置梯度为全1矩阵  --> 2 x 2
weight.grad = torch.ones((2, 2))
# 输出现有的weight和data
print("The data of weight before step:\n{}".format(weight.data))
print("The grad of weight before step:\n{}".format(weight.grad))
# 实例化优化器
optimizer = torch.optim.SGD([weight], lr=0.1, momentum=0.9)
# 进行一步操作
optimizer.step()
# 查看进行一步后的值，梯度
print("The data of weight after step:\n{}".format(weight.data))
print("The grad of weight after step:\n{}".format(weight.grad))
# 权重清零
optimizer.zero_grad()
# 检验权重是否为0
print("The grad of weight after optimizer.zero_grad():\n{}".format(weight.grad))
# 输出参数
print("optimizer.params_group is \n{}".format(optimizer.param_groups))
# 查看参数位置，optimizer和weight的位置一样，我觉得这里可以参考Python是基于值管理
print("weight in optimizer:{}\nweight in weight:{}\n".format(id(optimizer.param_groups[0]['params'][0]), id(weight)))
# 添加参数：weight2
weight2 = torch.randn((3, 3), requires_grad=True)
optimizer.add_param_group({"params": weight2, 'lr': 0.0001, 'nesterov': True})
# 查看现有的参数
print("optimizer.param_groups is\n{}".format(optimizer.param_groups))
# 查看当前状态信息
opt_state_dict = optimizer.state_dict()
print("state_dict before step:\n", opt_state_dict)
# 进行5次step操作
for _ in range(50):
    optimizer.step()
# 输出现有状态信息
print("state_dict after step:\n", optimizer.state_dict())
# 保存参数信息
torch.save(optimizer.state_dict(),os.path.join(r"D:\pythonProject\Attention_Unet", "optimizer_state_dict.pkl"))
print("----------done-----------")
# 加载参数信息
state_dict = torch.load(r"D:\pythonProject\Attention_Unet\optimizer_state_dict.pkl") # 需要修改为你自己的路径
optimizer.load_state_dict(state_dict)
print("load state_dict successfully\n{}".format(state_dict))
# 输出最后属性信息
print("\n{}".format(optimizer.defaults))
print("\n{}".format(optimizer.state))
print("\n{}".format(optimizer.param_groups))

输出结果：

# 进行更新前的数据，梯度
The data of weight before step:
tensor([[-0.3077, -0.1808],
        [-0.7462, -1.5556]])
The grad of weight before step:
tensor([[1., 1.],
        [1., 1.]])
# 进行更新后的数据，梯度
The data of weight after step:
tensor([[-0.4077, -0.2808],
        [-0.8462, -1.6556]])
The grad of weight after step:
tensor([[1., 1.],
        [1., 1.]])
# 进行梯度清零的梯度
The grad of weight after optimizer.zero_grad():
tensor([[0., 0.],
        [0., 0.]])
# 输出信息
optimizer.params_group is 
[{'params': [tensor([[-0.4077, -0.2808],
        [-0.8462, -1.6556]], requires_grad=True)], 'lr': 0.1, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'nesterov': False}]

# 证明了优化器的和weight的储存是在一个地方，Python基于值管理
weight in optimizer:1841923407424
weight in weight:1841923407424
    
# 输出参数
optimizer.param_groups is
[{'params': [tensor([[-0.4077, -0.2808],
        [-0.8462, -1.6556]], requires_grad=True)], 'lr': 0.1, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'nesterov': False}, {'params': [tensor([[ 0.4539, -2.1901, -0.6662],
        [ 0.6630, -1.5178, -0.8708],
        [-2.0222,  1.4573,  0.8657]], requires_grad=True)], 'lr': 0.0001, 'nesterov': True, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0}]

# 进行更新前的参数查看，用state_dict
state_dict before step:
 {'state': {0: {'momentum_buffer': tensor([[1., 1.],
        [1., 1.]])}}, 'param_groups': [{'lr': 0.1, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [0]}, {'lr': 0.0001, 'nesterov': True, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'params': [1]}]}
# 进行更新后的参数查看，用state_dict
state_dict after step:
 {'state': {0: {'momentum_buffer': tensor([[0.0052, 0.0052],
        [0.0052, 0.0052]])}}, 'param_groups': [{'lr': 0.1, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [0]}, {'lr': 0.0001, 'nesterov': True, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'params': [1]}]}

# 存储信息完毕
----------done-----------
# 加载参数信息成功
load state_dict successfully
# 加载参数信息
{'state': {0: {'momentum_buffer': tensor([[0.0052, 0.0052],
        [0.0052, 0.0052]])}}, 'param_groups': [{'lr': 0.1, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [0]}, {'lr': 0.0001, 'nesterov': True, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'params': [1]}]}

# defaults的属性输出
{'lr': 0.1, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'nesterov': False}

# state属性输出
defaultdict(<class 'dict'>, {tensor([[-1.3031, -1.1761],
        [-1.7415, -2.5510]], requires_grad=True): {'momentum_buffer': tensor([[0.0052, 0.0052],
        [0.0052, 0.0052]])}})

# param_groups属性输出
[{'lr': 0.1, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [tensor([[-1.3031, -1.1761],
        [-1.7415, -2.5510]], requires_grad=True)]}, {'lr': 0.0001, 'nesterov': True, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'params': [tensor([[ 0.4539, -2.1901, -0.6662],
        [ 0.6630, -1.5178, -0.8708],
        [-2.0222,  1.4573,  0.8657]], requires_grad=True)]}]

注意：

1. 每个优化器都是一个类，我们一定要进行实例化才能使用；
2. optimizer在一个神经网络的epoch中需要实现两个步骤：梯度置零、梯度更新；
3. 给网络不同的层赋予不同的优化器参数。

1.9.3 实验

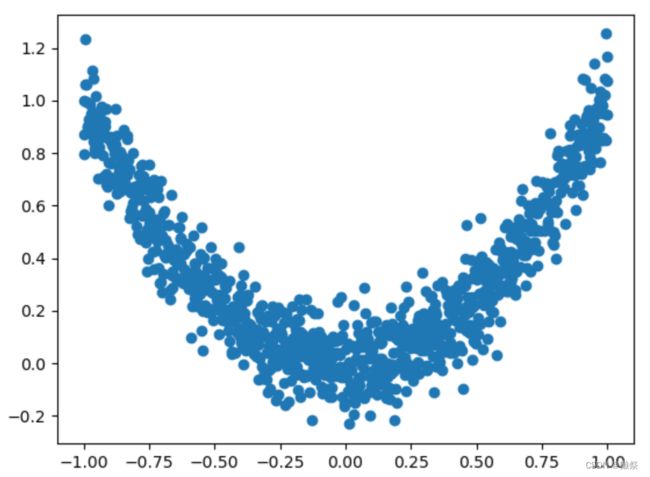
数据生成：

a = torch.linspace(-1, 1, 1000)
# 升维操作
x = torch.unsqueeze(a, dim=1)
y = x.pow(2) + 0.1 * torch.normal(torch.zeros(x.size()))

数据分布曲线：

网络结构：

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.hidden = nn.Linear(1, 20)
        self.predict = nn.Linear(20, 1)

    def forward(self, x):
        x = self.hidden(x)
        x = F.relu(x)
        x = self.predict(x)
        return x

测试结果图：