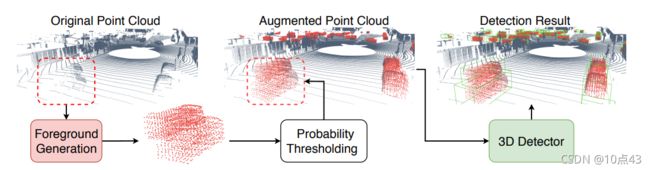
详解3D物体检测模型 SPG: Unsupervised Domain Adaptation for 3D Object Detection via Semantic Point Generation

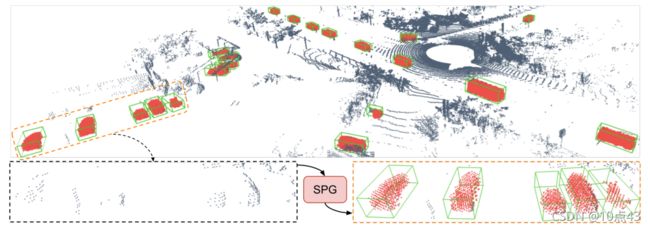
本文对基于激光雷达的无监督域自适应3D物体检测进行了研究，论文已收录于 ICCV2021。

在Waymo Domain Adaptation dataset上，作者发现点云质量的下降是3D物件检测器性能下降的主要原因。因此论文提出了Semantic Point Generation (SPG)方法，首先在预测的前景点区域生成语义点云，复原前景点物体缺失的部分。然后，将原始点云与生成的语义点云进行融合得到增强后的点云数据，再使用通用的3D物体检测器进行检测。在Waymo 和 KITTI 数据集上，无论是在target domain 还是 source domain上，本文提出的SPG方法都大幅提高了3D物检检测器的性能。

论文链接为：https://arxiv.org/pdf/2108.06709v1.pdf

---

1. Introduction

首先是引出本文要解决的问题：Waymo Open Dataset (OD)数据集是在California和Arizona收集的，而Waymo Kirkland Dataset (Kirk)是在Kirk收集的，这里将OD数据当作source domain，Kirk数据当作target domain。

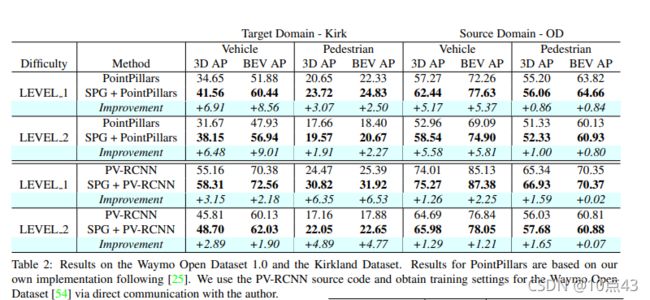
作者使用PointpPllars模型在OD训练集上训练，然后在OD和Kirk验证集上进行验证。从表1可以看出，雨天下收集到的点云质量下降很厉害，平均每帧缺失点数几乎是干燥天气下的两倍，检测性能也下降了27%左右；同时从Range Image上也可以看出雨天下物体点云缺失的区域也更不规则。

---

2. Semantic Point Generation

本文提出的SPG辅助检测方法如下图所示，SPG首先在预测的前景点区域生成语义点集，然后语义点集与原始点云相结合得到增强点云 $P{C}_{aug}$，最后再使用一个点云检测器得到检测结果。

2.1 Training Targets

设原始输入点云为 $P{C}_{raw}=\{p_1,p_2,...,p_N\}\in {\mathbb{R}}^{3+F}$，$3$ 表示点云坐标，$F$ 表示点云属性。

• SPG首先将原始点云划分为一个个Voxel，对于每一个Voxel，模型首先预测其为前景Voxel的概率 ${\tilde{P}}^f$，然后在每一个前景Voxel生成语义点集 $\widetilde{sp}$，其特征为 $\tilde{\psi }=[\tilde{\chi },\tilde{f}]$，分别表示语义点集的坐标和属性。
• 在与原始点云融合时只保留置信度超过 $P_{thresh}$ 的 $K$ 个点，得到增强后的点云$P{C}_{aug}=\left\{{\hat{p}}_1,{\hat{p}}_2,\dots ,{\hat{p}}_N,{\widetilde{sp}}_1,{\widetilde{sp}}_2,\dots ,{\widetilde{sp}}_K\right\}\in {\mathbb{R}}^{3+F+1}$，最后一个通道表示点为前景点的置信度，原始点云则置信度为 $1.0$，语义点集则置信度为 ${\tilde{P}}^f$。

在训练时，如果划分的Voxel为前景voxel $V^f$，则其对应类别 $y_i^f=1$，否则为 $y_i^f=0$。如果划分的Voxel非空的话， 令 ${\psi }_i=\left[{\bar{\chi }}_i,{\bar{f}}_i\right]$ 为回归目标，其中 $\overline{{\chi }_i}$ 为Voxel中所有前景点的平均坐标，${\bar{f}}_i$ 为前景点的属性平均值。

---

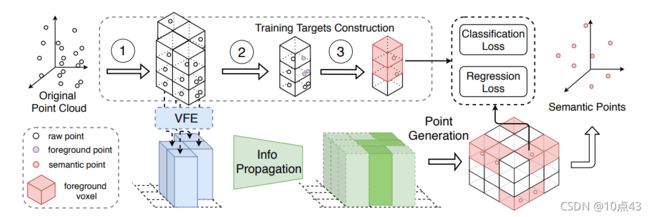
2.2 Model Structure

SPG模型结构由三部分组成：

• 首先是Voxle特征编码模块，对每一个Voxel进行特征学习，编码成pillars投影到鸟瞰图；
• 然后是信息传播模块，将非空pillars语义信息传播到附近非空pillars；
• 最后是语义点集生成模块，在每一个前景Voxel生成语义点集 ${\widetilde{sp}}_i=\left[{\tilde{\chi }}_i,{\tilde{f}}_i,{\tilde{P}}_i^f\right]$。

---

2.3 Foreground Region Recovery

为了在 empty areas 生成语义点集，作者设计了两个策略Hide and Predict和Semantic Area Expansion。

• Hide and Predict。原始点云 $P{C}_{raw}$ 划分为Voxel集合 $V=\{v_1,v_2,...,v_M\}$，在训练时，丢弃 $\gamma \%$的非空Voxel $V_{hide}$，SPG需要预测出这些隐藏的Voxel标签 $y^f$和对应点特征 $\tilde{\psi }$。
• Semantic Area Expansion。作者设计了一个扩展语义区域策略（图5所示），用以在empty space生成语义点集。具体地，非空和空的背景Voxel为 $V_o^b,V_e^b$，其对应标签为 $y^f=0$；非空前景Voxel $V_o^f$ 类别标签 $y^f=1$；bounding box中空的前景Voxel $V_e^f$ 类别标签为 $y^f=1$，同时增加一个权重系数 $\alpha <1$；监督学习非空前景Voxel $V_o^f$ 点集特征 $\psi$。图6为是否使用Expansion生成语义点集的效果。

---

2.4 Objectives

损失函数有两个，一个是类别损失函数，其中 $V_o$ 为非空Voxel，$V_e^b$ 为空的背景Voxel，$V_e^f$ 为空的前景Voxel，$V_{hide}$ 为隐藏的Voxel。

$$\begin{array}{rl}{L}_{cls}& =\frac{1}{\left|V_o\cup V_e^b\right|}\sum _{V_o\cup V_e^b}{L}_{\text{focal }}+\frac{\alpha }{\left|V_e^f\right|}\sum _{V_e^f}{L}_{\text{focal }}+\frac{\beta }{\left|V_{\text{hide }}\right|}\sum _{V_{\text{hide }}}{L}_{\text{focal }}\end{array}$$

另一个是点集回归损失函数：
$$\begin{array}{rl}{L}_{\text{reg }}& =\frac{1}{\left|V_o^f\right|}\sum _{V_o^f}{L}_{\text{smooth- }L1}(\tilde{\psi },\psi )+\frac{\beta }{\mid V_{\text{hide }}^f}\sum _{V_{\text{hide }}^f}{L}_{\text{smooth-L1 }}(\tilde{\psi },\psi )\end{array}$$

---

3. Experiments

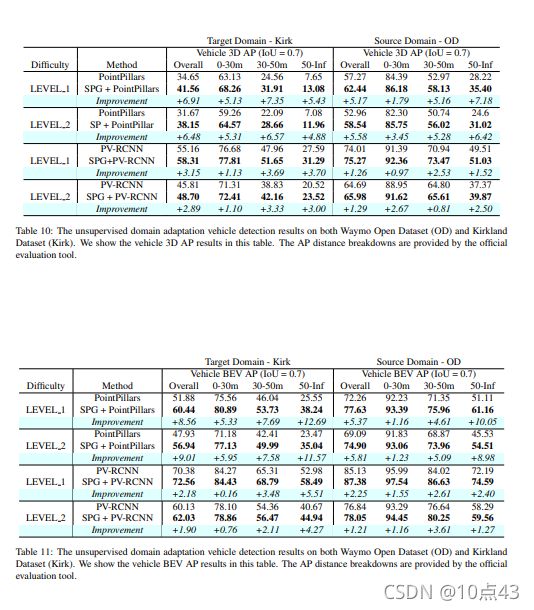
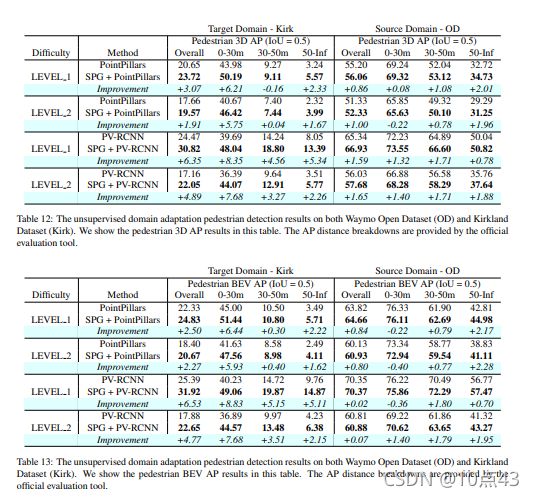
首先是在Waymo数据集上的检测结果：

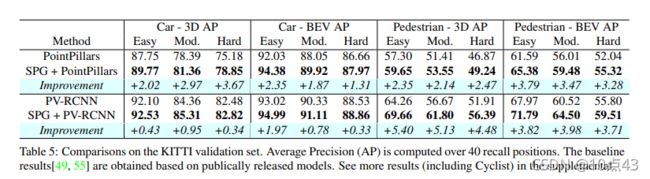
然后是在KITTI数据集上的检测结果。