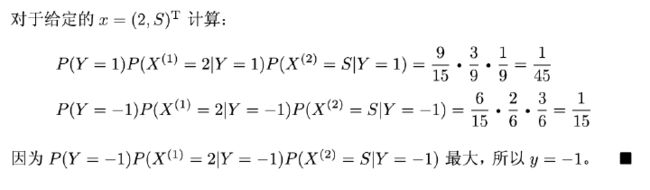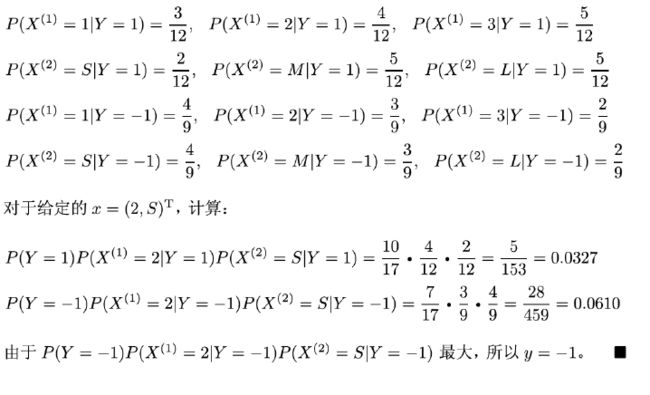朴素贝叶斯详细推导理解
文章目录
- 1. 公式推导
-
- 1.1 先验后验
- 1.2 条件概率公式
- 1.3 独立性假设
- 1.3 朴素贝叶斯推导
- 2. 朴素贝叶斯参数估计
-
- 2.1 极大似然估计
- 2.2 贝叶斯估计
1. 公式推导
1.1 先验后验
- 先验概率:事件发生前的预判概率。可以是基于历史数据的统计,可以由背景常识得出,也可以是人的主观观点给出。
- 后验概率:事件发生后求的反向条件概率;或者说,基于先验概率求得的条件概率。
1.2 条件概率公式
设有事件 A , B A,B A,B ,将已知 B B B 条件下求 A A A 的概率记作 P ( A ∣ B ) P(A|B) P(A∣B) ,将 A , B A,B A,B 两件事共同发生记作联合分布 P ( A , B ) P(A,B) P(A,B),所有有下列条件概率公式: P ( A ∣ B ) = P ( A , B ) P ( B ) \begin{aligned} P(A|B)=\frac{P(A,B)}{P(B)} \end{aligned} P(A∣B)=P(B)P(A,B)也即 P ( A , B ) = P ( B ) P ( A ∣ B ) \begin{aligned} P(A,B)=P(B)P(A|B) \end{aligned} P(A,B)=P(B)P(A∣B)又因为假设条件独立性,故 P ( A , B ) = P ( B , A ) P(A,B)=P(B,A) P(A,B)=P(B,A),所以带入上述公式可得 P ( A ∣ B ) = P ( B , A ) P ( B ) = P ( A ) P ( B ∣ A ) P ( B ) \begin{aligned} P(A|B) &= \frac{P(B,A)}{P(B)} \\ \\ &= \frac{P(A)P(B|A)}{P(B)} \end{aligned} P(A∣B)=P(B)P(B,A)=P(B)P(A)P(B∣A)这就是贝叶斯公式。
1.3 独立性假设
朴素贝叶斯假设条件概率是条件独立的,设 X , x X,x X,x 都是 n n n 维的向量, X X X 是定义在空间的随机向量, x x x 是输入, Y Y Y 是类标记,有 Y ∈ { c 1 , c 2 , ⋯ , c n } Y \in \{c_1,c_2, \cdots , c_n\} Y∈{c1,c2,⋯,cn},独立性可用下述公式来进行表达: P ( X = x ∣ Y = c k ) = P ( X ( 1 ) = x ( 1 ) , X ( 2 ) = x ( 2 ) , ⋯ , X ( n ) = x ( n ) ∣ Y = c k ) = ∏ j = 1 n P ( X ( j ) = x ( j ) ∣ Y = c k ) \begin{aligned} P(X=x|Y=c_k) &= P(X^{(1)}=x^{(1)},X^{(2)}=x^{(2)}, \cdots,X^{(n)}=x^{(n)}|Y=c_k) \\ &= \prod^{n}_{j=1}P(X^{(j)}=x^{(j)}|Y=c_k) \end{aligned} P(X=x∣Y=ck)=P(X(1)=x(1),X(2)=x(2),⋯,X(n)=x(n)∣Y=ck)=j=1∏nP(X(j)=x(j)∣Y=ck)其中的 X ( i ) = x ( i ) X^{(i)}=x^{(i)} X(i)=x(i) 表示 X , x X,x X,x 的第 i i i 个维度相等。
1.3 朴素贝叶斯推导
由贝叶斯公式和条件概率公式有 P ( Y = c k ∣ X = x ) = P ( X = x ∣ Y = c k ) P ( Y = c k ) P ( X = x ) = P ( X = x ∣ Y = c k ) P ( Y = c k ) ∑ h P ( X = x , Y = c h ) = P ( X = x ∣ Y = c k ) P ( Y = c k ) ∑ h P ( X = x ∣ Y = c h ) P ( Y = c h ) \begin{aligned} P(Y=c_k|X=x) &= \frac{P(X=x|Y=c_k)P(Y=c_k)}{P(X=x)} \\ \\ &= \frac{P(X=x|Y=c_k)P(Y=c_k)}{\sum_hP(X=x,Y=c_h)} \\ \\ &= \frac{P(X=x|Y=c_k)P(Y=c_k)}{\sum_hP(X=x|Y=c_h)P(Y=c_h)} \\ \end{aligned} P(Y=ck∣X=x)=P(X=x)P(X=x∣Y=ck)P(Y=ck)=∑hP(X=x,Y=ch)P(X=x∣Y=ck)P(Y=ck)=∑hP(X=x∣Y=ch)P(Y=ch)P(X=x∣Y=ck)P(Y=ck)将式 ( 4 ) (4) (4) 带入式 ( 5 ) (5) (5)可得到 P ( Y = c k ∣ X = x ) = P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) ∑ h P ( Y = c h ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c h ) \begin{aligned} P(Y=c_k|X=x) &= \frac{P(Y=c_k) \prod_j{P(X^{(j)}=x^{(j)}|Y=c_k)}}{\sum_hP(Y=c_h)\prod_jP(X^{(j)}=x^{(j)}|Y=c_h)} \end{aligned} P(Y=ck∣X=x)=∑hP(Y=ch)∏jP(X(j)=x(j)∣Y=ch)P(Y=ck)∏jP(X(j)=x(j)∣Y=ck) 这就是朴素贝叶斯的基本公式,所以其分类器可以表示为寻找一个最大的 c k c_k ck,即 y = f ( x ) = a r g m a x c k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) ∑ h P ( Y = c h ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c h ) \begin{aligned} y=f(x)=\mathop{argmax}\limits_{c_k}\frac{P(Y=c_k) \prod_j{P(X^{(j)}=x^{(j)}|Y=c_k)}}{\sum_hP(Y=c_h) \prod_jP(X^{(j)}=x^{(j)}|Y=c_h)} \end{aligned} y=f(x)=ckargmax∑hP(Y=ch)∏jP(X(j)=x(j)∣Y=ch)P(Y=ck)∏jP(X(j)=x(j)∣Y=ck)由于对于一个给定的训练集, 式 ( 7 ) (7) (7) 的分母是不变的,故只需要使得分子最大即可,即 y = a r g m a x c k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) \begin{aligned} y=\mathop{argmax}\limits_{c_k}{P(Y=c_k) \prod_j{P(X^{(j)}=x^{(j)}|Y=c_k)}} \end{aligned} y=ckargmaxP(Y=ck)j∏P(X(j)=x(j)∣Y=ck)
2. 朴素贝叶斯参数估计
2.1 极大似然估计
在贝叶斯中,学习就意味着对 P ( Y = c k ) P(Y=c_k) P(Y=ck) 和 P ( X ( j ) = x ( j ) ∣ Y = c k ) P(X^{(j)}=x^{(j)}|Y=c_k) P(X(j)=x(j)∣Y=ck) 进行估计和最大化。很自然的能够想到极大似然估计。
首先对 P ( Y = c k ) P(Y=c_k) P(Y=ck) ,其极大似然如下: P ( Y = c k ) = ∑ i = 1 N I ( y i = c k ) N \begin{aligned} P(Y=c_k)= \frac{\sum^{N}_{i=1}I(y_i=c_k)}{N} \end{aligned} P(Y=ck)=N∑i=1NI(yi=ck)即为数据中标签分类预测正确的数目百分比。
再对 P ( X ( j ) = x ( j ) ∣ Y = c k ) P(X^{(j)}=x^{(j)}|Y=c_k) P(X(j)=x(j)∣Y=ck) 进行极大似然估计,设第 j j j 个特征 x ( j ) x^{(j)} x(j) 的取值集合为 { a j 1 , a j 2 , ⋯ , a j n } \{ a_{j1}, a_{j2}, \cdots, a_{jn} \} {aj1,aj2,⋯,ajn} ,所以其极大似然估计如下 P ( X ( j ) = a j l ∣ Y = c k ) = ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) ∑ i = 1 N I ( y i = c k ) \begin{aligned} P(X^{(j)}=a_{jl}|Y=c_k)= \frac{\sum_{i=1}^{N}I(x_i^{(j)}=a_{jl},y_i=c_k)}{\sum_{i=1}^{N}I(y_i=c_k)} \end{aligned} P(X(j)=ajl∣Y=ck)=∑i=1NI(yi=ck)∑i=1NI(xi(j)=ajl,yi=ck)具体例子在这里截取李航老师的《统计学习方法》来做理解:
2.2 贝叶斯估计
使用极大似然估计时,可能出现所要求的概率为 0 0 0 的情况,该情况下就会十分影响其他概率的估计,故可以采用贝叶斯估计法。贝叶斯估计法描述如下: P λ ( X ( j ) = a j l ∣ Y = c k ) = ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) + λ ∑ i = 1 N I ( y i = c k ) + S j λ \begin{aligned} P_{\lambda}(X^{(j)}=a_{jl}|Y=c_k)= \frac{\sum_{i=1}^{N}I(x_i^{(j)}=a_{jl},y_i=c_k)+ \lambda}{\sum_{i=1}^{N}I(y_i=c_k)+S_j{\lambda}} \end{aligned} Pλ(X(j)=ajl∣Y=ck)=∑i=1NI(yi=ck)+Sjλ∑i=1NI(xi(j)=ajl,yi=ck)+λ当式中的 λ = 0 \lambda =0 λ=0 时,即是极大似然估计,当式中的 λ = 1 \lambda =1 λ=1 时,称之为拉普拉斯平滑。
同样的,先验概率 P λ ( Y = c k ) P_{\lambda}(Y=c_k) Pλ(Y=ck) 的表达如下: P λ ( Y = c k ) = ∑ i = 1 N I ( y i = c k ) + λ N + K λ \begin{aligned} P_{\lambda}(Y=c_k)= \frac{\sum^{N}_{i=1}I(y_i=c_k)+ \lambda}{N+K \lambda} \end{aligned} Pλ(Y=ck)=N+Kλ∑i=1NI(yi=ck)+λ具体例子在这里截取李航老师的《统计学习方法》来做理解: