【蓝桥杯真题】2016年省赛A组（C++）

        题目为本人学习、练习时写的，也参考了一些博客、网课（链接附在最后）。有些题目描述过于简便hhh~，也可以在网上搜索更详细的题目版本。

目录

题目1：猜年龄

题目2：吹蜡烛

题目3：填方格

题目4：快速排序

题目5：消除尾一

题目6：寒假作业

题目7：剪邮票

题目8：四平方和定理

题目9：密码脱落

题目10：

题目1：猜年龄

题目描述：“我的年龄是两位数，我比儿子大27岁，若把我的年龄位置交换，刚好为我儿子的年龄”，一共有多少种情况。

#include

using namespace std;

int main(){
	int ans = 0;
	for(int i=28; i<100; i++){
		int a=0,b=0;
		b = i%10;
		a = i/10;
		if((a+10*b)==(i-27)){
			ans++;
		}
	}	
	cout << ans << endl;
	return 0;
}

题目2：吹蜡烛

题目描述：每年吹与年龄相同根数的蜡烛，从某年开始到现在一共236根，求开始过生日的年龄。

#include

using namespace std;

int main(){
	for(int i=1; i<120; i++){
		int num=0;
		for(int j=i; j<120; j++){
			num += j;
			if(num==236){
				cout << i << " " << j;
				break;
			}	
		}
	}
	return 0;
}

题目3：填方格

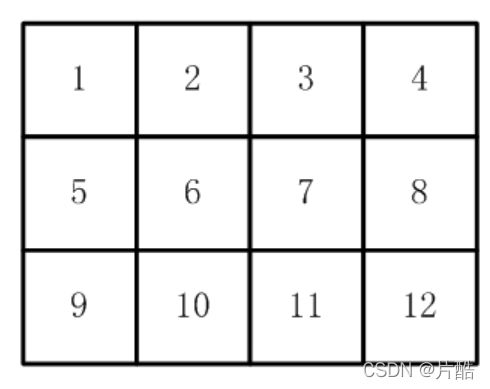
题目描述：在下列格子填入0-9， 连续两个数字不能相邻，一共有多少种方案？

#include
#include
#include
using namespace std;
int arr[10]={0,1,2,3,4,5,6,7,8,9};

bool check(){		
	if(abs(arr[0]-arr[1])==1||
	   abs(arr[0]-arr[3])==1||
	   abs(arr[0]-arr[4])==1||
	   abs(arr[0]-arr[5])==1||
	   
	   abs(arr[1]-arr[2])==1||
	   abs(arr[1]-arr[4])==1||
	   abs(arr[1]-arr[5])==1||
	   abs(arr[1]-arr[6])==1||
	   
	   abs(arr[2]-arr[5])==1||
	   abs(arr[2]-arr[6])==1||
	   
	   abs(arr[3]-arr[4])==1||
	   abs(arr[3]-arr[7])==1||
	   abs(arr[3]-arr[8])==1||
	   
	   abs(arr[4]-arr[5])==1||
	   abs(arr[4]-arr[7])==1||
	   abs(arr[4]-arr[8])==1||
	   abs(arr[4]-arr[9])==1||
	   
	   abs(arr[5]-arr[6])==1||
	   abs(arr[5]-arr[8])==1||
	   abs(arr[5]-arr[9])==1||
		
	   abs(arr[6]-arr[9])==1||
	   
	   abs(arr[7]-arr[8])==1||
	   abs(arr[8]-arr[9])==1) 
	   return false;

}


int main(){
	int ans = 0;
	do{
		if(check()){
			ans++;
		}
	}while(next_permutation(arr,arr+10));
	cout << ans << endl;
	return 0;
}

题目4：快速排序

题目描述：选一个标准，其左边元素不大于它，其右边元素不小于它。（代码填空）

#include
using namespace std;


void swap(int a[], int p, int r){
	int t = a[p];
    a[p] = a[r];
    a[r] = t;
}

int partition(int a[], int p, int r){
	int i = p;
    int j = r+1;
    int x = a[p];
    while(1){
		while(i x);
        if(i>=j) break;
        swap(a, i, j);
    }
    swap(a, p, j);//填空代码
    return j;
}

void quicksort(int a[], int p, int r){
	if(p

题目5：消除尾一

题目描述：把一个整数的二进制表示的最右边连续的1全部变成0，如果最后一位是0，则原数字保持不变。（代码填空）

#include

void f(int x){
	int i;
	for(i=0; i<32; i++){
		printf("%d", (x>>(31-i))&1);//输出二进制数 
	}
	printf("   ");
	
	x = (x+1)&x;//填空  加一后 连续的一变成零 多出来一个一和原来的零与后还是零
	
	for(i=0; i<32; i++){
		printf("%d", (x>>(31-i))&1);
	}
	printf("\n");
}

int main(){
	
	f(103);
	f(12);
	return 0;
}

题目6：寒假作业

题目描述：在下列括号内填写1-13某个数字，但不能重复，一共有几种方案。（结果填空）

（）+（）=（）

（）-（）=（）

（）×（）=（）

（）÷（）=（）

#include
int ans;
using namespace std;
int a[13]={1,2,3,4,5,6,7,8,9,10,11,12,13};
bool check(){
	if(a[0]+a[1]==a[2]&&
	   a[3]-a[4]==a[5]&&
	   a[6]*a[7]==a[8]&&
	   a[9]/a[10]==a[11]&&
	   a[9]%a[10]==0)
	   return true;
	return false;
}

void f(int k){//全排列
	if(k==13){
		if(check()){
			ans++;
		}
	}
	for(int i=k; i<13; i++){
		int t = a[i]; a[i] = a[k]; a[k] = t;
		if(k==2&&a[0]+a[1]!=a[2]){//提前检查 加快速度 
			t = a[i]; a[i] = a[k]; a[k] = t;
			continue;
		}
		f(k+1);
		t = a[i]; a[i] = a[k]; a[k] = t;
	}
}

int main(){
	f(0);
	cout << ans << endl;
}

题目7：剪邮票

题目描述：共12张中剪出5张，这5张需连通。一共有多少种不同的剪取方法。请填写表示方案数目的整数。

#include
#include
#include
using namespace std;
int ans=0;
void dfs(int g[3][4], int x, int y){//连通检查
	g[x][y]=0;
	if(x-1>=0&&g[x-1][y]==1){
		dfs(g, x-1, y);	
	}
	if(x+1<=2&&g[x+1][y]==1){
		dfs(g, x+1, y);
	}
	if(y-1>=0&&g[x][y-1]==1){
		dfs(g, x, y-1);
	}
	if(y+1<=3&&g[x][y+1]==1){
		dfs(g, x, y+1);
	}
} 

bool check(int a[13])
{
	int g[3][4], count=0;
	for(int i=0; i<3; i++){
		for(int j=0; j<4; j++){
			if(a[i*4+j]==1){
				g[i][j] = 1;
			}else{
				g[i][j] = 0;
			}
			
		}
	}
	
	for(int i=0; i<3; i++){
		for(int j=0; j<4; j++){
			if(g[i][j]==1){
				dfs(g, i, j);
				count++;
			}
		}
	}
	
	if(count==1){//一次连通 搜索后 全为0
		return true;
	}
	else{
		return false;
	}
}

int main(){
	int a[]={0,0,0,0,0,0,0,1,1,1,1,1};
	do{
		if(check(a)){
			ans++;
		}
	}while(next_permutation(a,a+12));
	cout << ans << endl; 
	return 0;
}

题目8：四平方和定理

题目描述：四平方和定理又称为拉格朗日定理：每个正整数都可以表示为至多4个正整数的平方和。如果把0包括进去，就正好可以表示为4个数的平方和

#include
#include
using namespace std;
typedef long long int ll;
 
int main(){
	ll N;
	cin >> N;
	for(int i=0; i*i

题目9：密码脱落

题目描述：X星球的考古学家发现了一批古代留下来的密码。 这些密码是由A、B、C、D 四种植物的种子串成的序列。 仔细分析发现，这些密码串当初应该是前后对称的（也就是镜像串）。 由于年代久远，其中许多种子脱落了，因而可能会失去镜像的特征。

你的任务是： 给定一个现在看到的密码串，计算一下从当初的状态，它要至少脱落多少个种子，才可能会变成现在的样子。

输入一行，表示现在看到的密码串（长度不大于1000） 要求输出一个正整数，表示至少脱落了多少个种子。

#include
#include
#include
using namespace std;
char s1[1000];
int dp[1000][1000];
char s2[1000];

int lcs(const char *s1, const char *s2, int len){//求最大公共子串 	
	for(int i=1; i<=len; i++){
		for(int j=1; j<=len; j++){
			if(s2[j-1]==s1[i-1]){
				dp[i][j] = dp[i-1][j-1] + 1;
			}
			else{
				dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
			}
		}
	} 
	return dp[len][len];
}
int main(){
	cin >> s1;
	int len = strlen(s1);
	for(int i=0; i

题目10：最大比例系数

题目描述：

X星球的某个大奖赛设了M级奖励。每个级别的奖金是一个正整数。并且，相邻的两个级别间的比例是个固定值。也就是说：所有级别的奖金数构成了一个等比数列。比如：16,24,36,54.其等比值为：3/2。现在，我们随机调查了一些获奖者的奖金数。请你据此推算可能的最大的等比值。

输入第一行为数字 N (0

输出一个形如A/B的分数，要求A、B互质。表示可能的最大比例系数

测试数据：

①输入：3      1250 200 32

输出：25/4

②输入：4      3125 32 32 200

输出：5/2

③输入：3      549755813888 524288 2

输出：4/1

#include
#include
#include
#include

参考资料：

蓝桥杯历年真题及详细解答_元气算法的博客-CSDN博客_蓝桥杯真题

【蓝桥杯】2013年-2018年蓝桥杯C／C++大学A组省赛真题_哔哩哔哩_bilibili