Conditional Channel Gated Networks for Task-Aware Continual Learning论文阅读+代码解析

本篇论文来自2020年ECCV，论文地址点这里

一. 介绍

机器学习和深度学习模型通常是离线训练的，然而，当在现实环境中进行在线培训时，模型可能会遇到多个任务作为一个连续的活动流，而不知道它们之间的关系或持续时间。在这种情况下，深度学习模型会遭受灾难性遗忘，这意味着它们会丢弃以前获得的知识，以适应当前的观察结果。导致这样的根本原因是，在学习新任务时，模型会覆盖对以前任务至关重要的参数。
持续学习研究（也称为终身学习或增量学习）解决了上述问题。大多数文献中所考虑的典型环境是一个模型逐个学习不相交的分类问题。根据应用程序的要求，应该分析当前输入的任务可能是已知的，也可能是未知的。文献中的大多数方法都假设任务的标签是在推理过程中提供的。这种持续学习环境通常称为任务增量。在许多实际应用中，例如分类和异常检测系统，只要训练流中出现新类，模型就可以无缝地实例化新任务。然而，一旦部署到野外，它就必须处理输入，而不知道在哪项训练任务中会遇到类似的观察结果。这种情况下，任务标签仅在培训期间可用，称为类增量。现有的方法采用不同的策略来缓解灾难性遗忘，例如记忆缓冲、知识提炼、突触巩固和参数掩蔽。然而，最近的证据表明，只要在测试时任务标签不可用，现有的解决方案即使对于简单的数据集也会失败。
本文介绍了一种基于条件计算的解决方案，用于解决任务增量和分类增量学习问题。具体来说，我们的框架依赖于单独的特定于任务的分类头（多头架构），并且在（共享）特征提取器的每一层中都使用了通道选通，并且在类增量的学习环境中进行监督任务预测的工作。

二. 模型

2.1 问题定义与目标

我们有一个参数网络，称为学习网络/主干网络。其会经历一系列的$N$个任务，$\mathcal{T}=\{T_1,\cdots ,T_N\}$。每一个任务$T_i$为一个分类的任务，$T_i={\left\{{\mathbf{x}}_j,y_j\right\}}_{j=1}^{n_i}$，其中${\mathbf{x}}_j\in {\mathbb{R}}^m$,$y_j\in \{1,\cdots ,C_i\}$。那么对于一个任务增量的设置下，我们的优化目标为：
$$\underset{\theta }{\max }{\mathbb{E}}_{\mathbf{t}\sim \mathcal{T}}\left[{\mathbb{E}}_{(\mathbf{x},\mathbf{y})\sim T_{\mathbf{t}}}\left[\log p_{\theta }(\mathbf{y}\mid \mathbf{x},\mathbf{t})\right]\right]$$
其中$\theta$表示学习者网络的参数化，$\mathbf{x},\mathbf{y},\mathbf{t}$分别是与每个样本的特征、标签和任务相关的随机变量。这样的最大化问题受到持续学习的约束：由于模型连续观察任务，上面等式中的外部期望很难计算或近似。值得注意的是，此设置要求假设每个样本所属任务标签在训练和测试阶段都是已知的。在实践中，可以利用这些信息来隔离分类器的相关输出单元，防止属于不同任务的类之间通过同一softmax层（多头）进行竞争。
对于类增量来说，模型需要做下面的优化：
$$\underset{\theta }{\max }{\mathbb{E}}_{\mathbf{t}\sim \mathcal{T}}\left[{\mathbb{E}}_{(\mathbf{x},\mathbf{y})\sim T_{\mathbf{t}}}\left[\log p_{\theta }(\mathbf{y}\mid \mathbf{x})\right]\right]$$
在这里，没有任务条件限制会阻止模型中任何形式的任务感知推理。此设置要求将输出单元合并到单个分类器（单头）中，在该分类器中，来自不同任务的类相互竞争，通常会导致更严重的遗忘。虽然模型可以根据任务信息进行学习，但在推理过程中无法获得这些信息。
为了处理未知任务的观察结果，同时保留多头部设置的优点，我们将共同优化类和任务预测，如下所示：
$$\begin{array}{rl}\underset{\theta }{\max }& {\mathbb{E}}_{\mathbf{t}\sim \mathcal{T}}\left[{\mathbb{E}}_{(\mathbf{x},\mathbf{y})\sim T_{\mathbf{t}}}\left[\log p_{\theta }(\mathbf{y},\mathbf{t}\mid \mathbf{x})\right]\right]=\\ & {\mathbb{E}}_{\mathbf{t}\sim \mathcal{T}}\left[{\mathbb{E}}_{(\mathbf{x},\mathbf{y})\sim T_{\mathbf{t}}}\left[\log p_{\theta }(\mathbf{y}\mid \mathbf{x},\mathbf{t})+\log p_{\theta }(\mathbf{t}\mid \mathbf{x})\right]\right].\end{array}$$
此式子描述了两个优化目标。一方面，$\log p_{\theta }(\mathbf{y}\mid \mathbf{x},\mathbf{t})$表示根据任务进行的类别分类，和第一个式子中多头分类类似。另一方面式子$\log p_{\theta }(\mathbf{t}\mid \mathbf{x})$会预测观察到的样本属于哪一个任务，此预测依赖于任务分类器，任务分类器以
单头的方式递增训练。值得注意的是，此等式的目标将单头转换为预测任务的级别，这样能保证不同任务之间不会进行竞争。

3.2 类标签的多头学习

上图为这部分的主要工作。考虑${\mathbf{h}}^l\in {\mathbb{R}}^{c_{in}^l,h,w}$以及${\mathbf{h}}^{l+1}\in {\mathbb{R}}^{c_{\text{out }}^l,h^{\prime },w^{\prime }}$为第$l$层的对饮对应的卷积的输入输出。 我们代替${\mathbf{h}}^{l+1}$，我们将向下一层转发一个稀疏特征映射${\hat{\mathbf{h}}}^{1+1}$（通过修剪非信息通道获得）。在任务$t$的训练期间，关于必须激活哪些通道的决定被委托给选通模块$G_t^l$，该模块取决于输入功能图${\mathbf{h}}^l$：
$${\hat{\mathbf{h}}}^{l+1}=G_t^l\left({\mathbf{h}}^l\right)\odot {\mathbf{h}}^{l+1}$$
其中$G_t^l\left({\mathbf{h}}^l\right)=\left[g_1^l,\dots ,g_{c_{\text{out }}^l}^l\right],g_i^l\in \{0,1\}$，$\odot$表示为通道上的乘法。为了符合增量设置，每次模型观察新任务的示例时，我们都会实例化一个新的选通模块。然而，每个模块都被设计成一个轻量级网络，计算成本和参数数量可以忽略不计。具体而言，每个选通模块包括一个多层感知器（MLP），其中一个隐藏层具有16个单元，然后是一个批量规范化层和一个ReLU激活。最终的线性映射为卷积的每个输出通道提供对数概率（softmax）。
通过门反向传播梯度具有挑战性，因为采用不可微阈值来进行二进制开/关决策。因此，我们依赖GumbelSoftmax抽样，来进行估计。具体来说，在正向过程中使用硬阈值（零中心），在反向过程中使用sigmoid函数（使用温度超参数$\tau =2/3$）。
更多的，我们以稀疏性为目标惩罚卷积核的数量：
$${\mathcal{L}}_{\text{sparse }}={\mathbb{E}}_{(\mathbf{x},\mathbf{y})\sim T_{\mathbf{t}}}\left[\frac{{\lambda }_s}{L}\sum _{l=1}^L\frac{{\Vert G_t^l\left({\mathbf{h}}^l\right)\Vert }_1}{c_{\text{out }}^l}\right]$$
其中$L$表示为整个门网络的数量，${\lambda }_s$表示为控制这个稀疏程度的超参数。稀疏性目标指示每个选通模块选择一组最小的内核，允许我们保留过滤器以优化未来任务。此外，它使我们能够根据任务的难度和手头的观察情况，有效地调整分配网络的容量。这种数据驱动的模型选择与其他使用固定比率进行模型增长或权重修剪的持续学习策略形成对比。
在优化任务$t$之后，我们在验证集$T_t^{val}$为每一个单元计算一个相关性得分$r_k^{l,t}$，来表示其命中门网络的可能性：
$$r_k^{l,t}={\mathbb{E}}_{(\mathbf{x},\mathbf{y})\sim T_{\mathrm{t}}^{\text{val }}}\left[p\left(\mathbb{I}\left[g_k^l=1\right]\right)\right]$$
经过计算，我们可以获得两组不同的kernel。一是，我们可以冻结住和任务$t$相关的kernel，防止其受到干扰。第二，我们可以重新初始化那些不相关的kernel，使其能够重新学习新的任务。

3.3 任务标签的单头学习

为了能够保证模型根据数据识别出不同的样本，我们的解决方案是部署所有的门网络$[G_1^l,\cdots ,G_t^l]$，然后计算其对应的输出$\left[{\hat{\mathbf{h}}}_1^{l+1},\dots ,{\hat{\mathbf{h}}}_t^{l+1}\right]$，这样依次传递下去。这种机制在网络中生成并行计算流，共享相同的层，但为每个层选择不同的单元集来激活，如下图：

经过最后一层的计算后，我们可以获得$t$个候选的特征图$\left[{\hat{\mathbf{h}}}_1^{L+1},\dots ,{\hat{\mathbf{h}}}_t^{L+1}\right]$。任务分类器由所有的特征映射串联而成：
$$h=\underset{i=1}{\overset{t}{⨁}}\left[\mu \left({\hat{\mathbf{h}}}_i^{L+1}\right)\right],$$
其中$\mu$表示为全局平均池化，而$⨁$表示为按照特征轴进行连接的函数。任务分类器的架构基于一个浅层MLP，其中一个隐藏层具有64个ReLU单元，然后是预测任务标签的softmax层。我们使用标准交叉熵目标来训练任务分类器。
单头任务分类器面临灾难性遗忘。最近的论文表明，基于记忆重放的策略代表了单头环境中最有效的持续学习策略。因此，我们选择通过排练来改善这个问题。（存下样本，之后使用）。

三. 代码解读

代码链接点这里
在解读代码前，我们来看一下本文的两个优化目标：基于任务增量的模型训练以及基于任务编号的任务样本识别。其中，第一个就是常规的训练模式，对于每个任务我们都有其对应的标号（index），在训练的时候这些标号会一起进行使用。作者这里使用的是参数隔离的方法，其设计了一个门控网络，能够针对于每个任务激活卷积核的程度来识别网络结构，为每个任务创造了单独的内核。第二个是根据数据样本和任务编号来训练任务识别模块，这里需要存储以前任务的样本，在训练的时候将每个任务+其对应的编号依次传入，然后进行训练使得之后模型能够快速根据样本识别对应的任务。
首先我们看一下整个网络结构：包括backbone特征提取+task_clf任务分类+multihead_clf类别分类网络


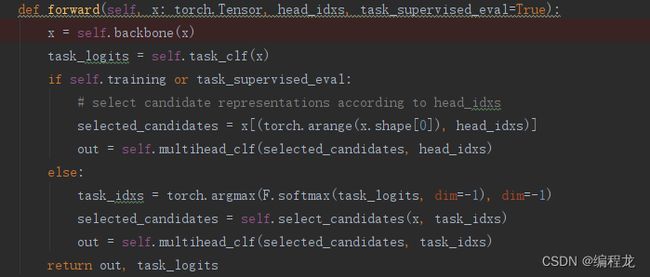
在backbone中涉及到门控网络：
首先，我们来了解一下基本的卷积快构成：

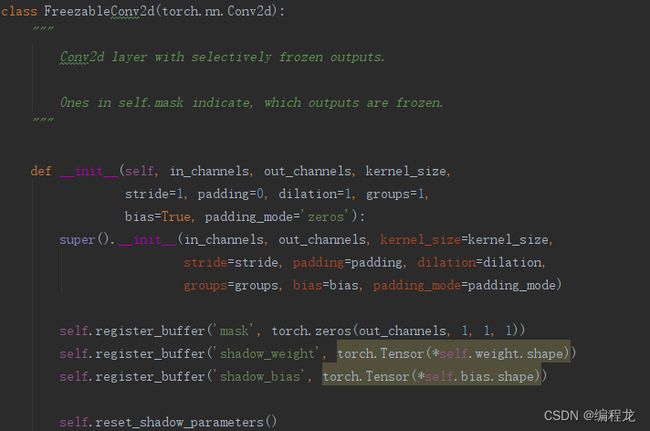
可以发现，作者使用了掩码来进行处理，以方便冻结之前的FIlter。然后每个卷积层中有对应的门控函数以及对应的BatchNorm层（第2节内容讲到的）：


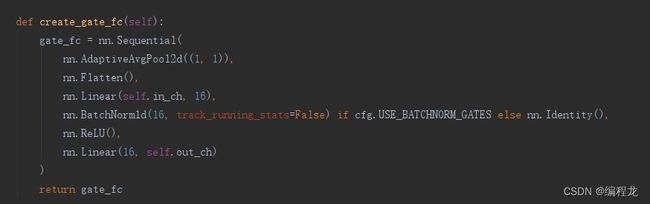
存在self.gates中，可以发现其就为一系列MLP操作。接下来我们来看一看每个conv的前向传播过程：

首先经过self.main_conv_path()输出得到卷积的结果，然后根据每一个任务id，使用self.select_channels_for_task()函数计算出门控后选择的filter：

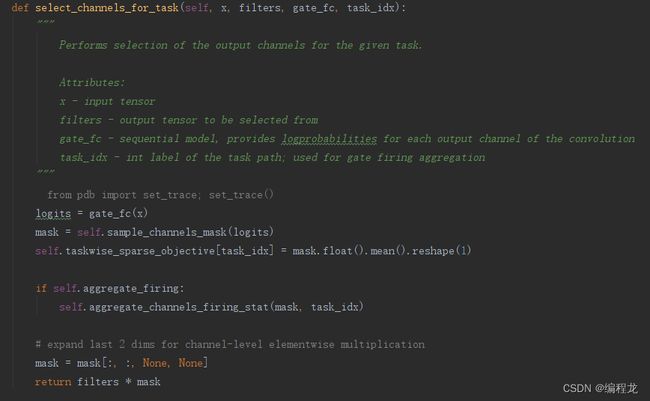
注意在进行门控计算的时候，提到了使用gumbel_sigmoid计算，避免不可唯微分的情况，如下：

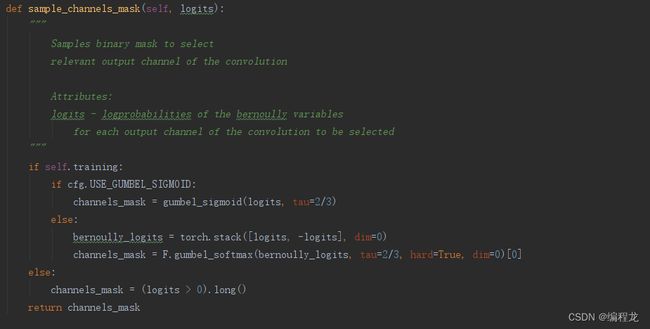
这里经过每个conv的时候都需要对每一个任务的门控都计算一遍，这是因为我们不仅需要对当前任务的class分类，也要对task的sample进行分类学习。
然后在任务分类网络中：

其实很简单，首先对最后一层门输出的t个任务结果进行合并然后pooling最后使用两个全连接进行工作。
最后就是训练过程的计算：

可以发现包括三个损失：head_loss样本分类损失+task_loss任务分类损失以及一个稀疏化损失，其中稀疏化的损失计算如下：