【SIFT】超详详详解 - 实现细节记录
目录
- 前言
- 一、尺度空间的生成:高斯金字塔 Gaussian pyrmid
-
- 1、图像的尺度空间 - 高斯金字塔 Gaussian pyramid
- 2、高斯金字塔的组 与 组数 Octave
-
- 1)组
- 2)组数
- 3)升采样获得 base image
- 3、高斯金字塔的层与层数 interval+3
-
- 1)层
- 2)层数
- 4、空间尺度 σ \sigma σ 与 空间尺度的初始值 σ 0 \sigma_0 σ0
-
- 1)空间尺度 σ \sigma σ
- 2)空间尺度的初始值 σ 0 \sigma_0 σ0
- 二、关键点的检测
-
- 1、LoG(Laplacian of Gaussian)与 DoG(Difference of gaussian)
-
- 1)Laplacian 的定义
- 2)LoG 的定义 (Laplacian of Gaussian)
- 3) 可用 DoG 近似 LoG
- 2、高斯差分金字塔(DOG:difference of gaussian)
- 3、在DOG中找极值点
- 4、 尺度连续性
- 三、精确定位极值点
-
- 1、使用子像素插值法,根据 Taylor公式 拟合出精确的亚像素极值点
- 2、消除边缘相应
- 四、关键点方向分配
-
- 1、3σ邻域窗口
- 2、关键点的梯度值 与 梯度方向
- 3、梯度直方图
- 4、梯度直方图的平滑处理
- 5、关键点的 主方向 和 辅方向
- 五、关键点的特征描述
-
- 1. 确定计算描述子所需的图像区域
- 六、总结
- 附:
前言
英文部分皆摘于论文原文
- SIFT (Scale-invariant feature transform):尺度不变特征变换
- 1999年,由 David Lowe 首先发表于计算机视觉国际会议 ICCV(International Conference on Computer Vision)。2004年,再次经过 David Lowe 整理完善后,发表于 IJCV(International Journal of Computer Vision)
This approach has been named the Scale Invariant Feature Transform (SIFT), as it transforms
image data into scale-invariant coordinates relative to local features.
- 作用:找出图像关键点 (extract keypoints)+ 生成每个关键点的描述子(generate descriptors for each keypoint)
Large numbers of features can be extracted from typical images with eficient algorithms. In addition, the features are highly distinctive, which allows a single feature to be correctly matched with high probability against a large database of features, providing a basis for object and scene recognition.
-
SIFT 特征具有以下属性 :
(1)是图像的局部特征
(2)对图像尺度缩放,图像旋转,具有不变性
(3)对亮度变化,3D相机视点,具有一定的不变性
(4)在遮挡,杂波,噪声的情况下,也能保持一定程度的稳定性The features are invariant to image scaling and rotation, and partially invariant to change in illumination and 3D camera viewpoint. They are well localized in both the spatial and frequency domains, reducing the probability of disruption by occlusion, clutter, or noise.
-
提取图像SIFT特征描述子的过程:(我这里比作者原文多拎了第一步 “空间尺度生成” 出来)
(1)尺度空间的生成(这里的尺度空间采用高斯尺度空间:高斯金字塔 - Gaussian pyrmid)
(2)尺度空间极值点检测 (找出极值点作为关键点)
(3)精确定位关键点(从关键点的离散位置表达,拟合出连续的位置表达)
(4)关键点区域方向分配(圈出关键点的邻域,用直方图统计邻域中像素点的方向,确定关键点的方向)
(5)生成关键点描述子
- 提取出的图像特征描述子有什么作用呢?
假设有两张图像,分别是同一个场景下,不同角度不同距离拍摄的。分别将两张图像中的关键点找出,并生成这些关键点的特征描述子。对比两张图像的关键点的描述子,可以得到两张图像中关键点的匹配关系。这样就能再进行更下游的任务了。比如,物体识别/场景识别,多幅图像的三维结构求解,立体匹配,运动跟踪,等等。
Image matching is a fundamental aspect of many problems in computer vision, including object or scene recognition, solving for 3D structure from multiple images, stereo correspondence, and motion tracking.
This paper describes image features that have many properties that make them suitable for matching differing images of an object or scene.
一、尺度空间的生成:高斯金字塔 Gaussian pyrmid
为什么要做高斯金字塔?为了尺度不变性。
对同一个物体做不同距离的拍照:
- 离得近,物体拍得大,对应的是小尺度,得到的是物体的细节
- 离得远,物体就拍得小,对应的是大尺度,得到的是物体的轮廓
如果我们的目标是:不论距离远近,都能检测出物体稳定的关键点,就需要在图像的各个尺度上进行检测。高斯金字塔就是将图像进行缩放和模糊,生成各个尺度的图像,从而使得我们可以在各个尺度上进行关键点检测以及描述子的提取。
1、图像的尺度空间 - 高斯金字塔 Gaussian pyramid
图像的尺度是由 L ( x , y , σ ) L_{(x, y, \sigma)} L(x,y,σ)来定义的,它是高斯核 G ( x , y , σ ) G_{(x, y, \sigma)} G(x,y,σ) 和 原图像 I ( x , y ) I_{(x, y)} I(x,y)的卷积的结果。
L ( x , y , σ ) = G ( x , y , σ ) ∗ I ( x , y ) G ( x , y , σ ) = 1 2 π σ 2 e − ( x 2 + y 2 ) / 2 σ 2 L_{(x, y, \sigma)} = G_{(x, y, \sigma)} * I_{(x, y)}\\ \ \\ G_{(x, y, \sigma)} = \frac{1}{2\pi\sigma^2}e^{-(x^2+y^2)/2\sigma^2} L(x,y,σ)=G(x,y,σ)∗I(x,y) G(x,y,σ)=2πσ21e−(x2+y2)/2σ2
高斯核尺度参数 σ \sigma σ 是一个变量,具有不同尺度参数 σ \sigma σ 的高斯核 和原图像做卷积运算,就定义了具有不同空间尺度的图像。
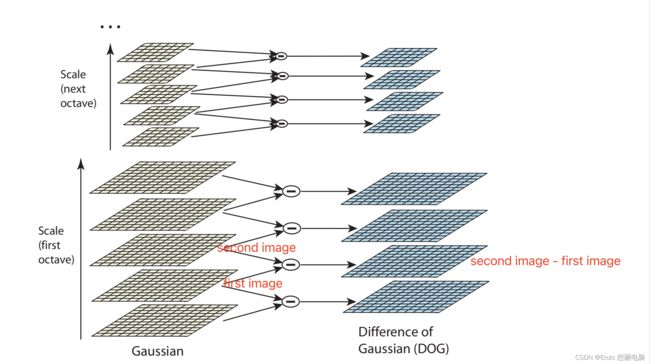
当一个图像与一系列 (尺度参数 σ \sigma σ 连续增加的) 高斯核做卷积,就生成了一系列的高斯模糊图像,这一系列高斯模糊图像就构成了 图像的尺度空间。再通过间隔的降采样,就形成了高斯金字塔(高斯尺度空间)
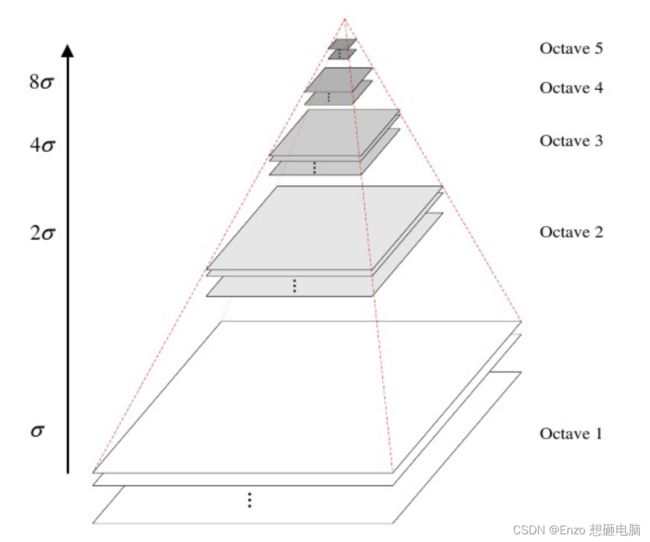
高斯金字塔(Gaussian Pyramid) 是采用高斯函数对图像进行模糊以及降采样处理得到。
octave 表示组,上图中有 5组,每组中有多张图片(一般为3~6张)
2、高斯金字塔的组 与 组数 Octave
1)组
octave 代表组,每组中的图像有相同的尺寸,而不同组间的图像尺寸不一样。上面组的尺寸为下面组的尺寸的1/4 (高度为1/2,宽度为1/2) (这里"上面下面" 说的是其在金字塔中的位置,不是按照索引号来说的。若按照索引号来说,或者说,按照处理顺序来说,是下一组 octave+1 中的图像尺寸是 上一组 octave 中图像尺寸 的1/4)
2)组数
高斯金字塔的组数 是由图像的尺寸决定的。由于每下一组图像的尺寸是上一组图像尺寸的1/4,图像的尺寸随着组数的增加持续递减,直到图像长和宽中较小的那个,不小于4为止。计算公式为: o c t a v e = log 2 m i n ( M , N ) − 1 octave = \log_2^{min(M, N)} - 1 octave=log2min(M,N)−1
3)升采样获得 base image
为了尽可能多的保留原始图像信息,一般需对原始图像进行扩大 2倍采样(升采样),得到的图像会作为基图像(base image),后续的操作都是基于 base image 展开。
假设原图像的尺寸为 256*256,升采样得到 base image 尺寸为 512*512,然后基于base image 的尺寸进行计算,得组数为: o c t a v e = log 2 m i n ( 512 , 512 ) − 1 = 8 octave= \log_2^{min(512, 512)} - 1 =8 octave=log2min(512,512)−1=8
| 金字塔层数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 图像大小 | 512*512 | 256*256 | 128*128 | 64*64 | 32*32 | 16*16 | 8*8 | 4*4 |
3、高斯金字塔的层与层数 interval+3
1)层
金字塔每组中的图像称为层
- 第1组第1层的图像是 base image,其根据原图像升采样而得,升采样采用双线性插值法 :INTER_LINEAR
image = resize(image, (0, 0), fx=2, fy=2, interpolation=INTER_LINEAR)
- 第2组(及以上组) 的第1层 是基于上一组的倒数第3层图像降采样得到。
降采样方式为直接删除偶数行和偶数列,使用函数为 最临近插值法 INTER_NEAREST
octave_base = gaussian_images_in_octave[-3]
image = resize(octave_base, (int(octave_base.shape[1]/2), int(octave_base.shape[0]/2)), interpolation=INTER_NEAREST)
- 第2组(及以上组) 的第2层(及以上层),是基于本组第1层图像进行高斯模糊得到
高斯模糊模糊这里就不赘述了,请参考文章
高斯模糊的参数 σ \sigma σ 的取值规则下面介绍
image = GaussianBlur(image, (0, 0), sigmaX=gaussian_kernel, sigmaY=gaussian_kernel)
2)层数
大家可能看到很多地方直接用 interval 来表示高斯金字塔每组里图像的层数,其实是不准确的。
interval 是间隔的意思,是用来表示高斯差分金字塔DoG的层数(后面会说到)。因为 DoG 是高斯金字塔中相邻的2层相减,DoG每组的层数 就是高斯金字塔每组中层的间隔数,所以用 interval 这个单词来表示 DoG的层数是很make sense 的。
然后,为了保证图像尺度变化的连续性,我们希望 DOG 每组的层数为 interval+2, 所以,高斯金字塔的层数就是interval+3。 (“尺度变化的连续性”在 第二部分-关键点的检测 的第4点详细说明,也会解释为什么层数是 interval+3)
4、空间尺度 σ \sigma σ 与 空间尺度的初始值 σ 0 \sigma_0 σ0
1)空间尺度 σ \sigma σ
尺度变化公式如下:(公式中 组与层的索引皆从1开始)
2 i − 1 ( σ , k σ , k 2 σ , . . . , k n − 1 σ ) , 其 中 k = 2 1 N 2^{i-1}(\sigma, k\sigma, k^2\sigma, ..., k^{n-1}\sigma), 其中 k = 2^{\frac{1}{N}} 2i−1(σ,kσ,k2σ,...,kn−1σ),其中k=2N1
其中,
- σ \sigma σ :初始尺度,就是 σ 0 \sigma_0 σ0, σ 0 = 1.6 \sigma_0=1.6 σ0=1.6
- i i i :组索引, 从1开始
- n n n:层索引,从1开始
- N N N :金字塔每组的层数, N = i n t e r v a l + 3 = 6 N = interval +3 = 6 N=interval+3=6
由此可见,相邻两组的同一尺度为2倍的关系
例如,第2组第3层的尺度为: σ = 2 i − 1 k n − 1 σ = 2 2 − 1 ∗ 2 1 6 ( 3 − 1 ) ∗ 1.6 = 4.222 \sigma = 2^{i-1}k^{n-1}\sigma = 2^{2-1}*2^{\frac{1}{6}(3-1)}*1.6 = 4.222 σ=2i−1kn−1σ=22−1∗261(3−1)∗1.6=4.222
还有一种公式写法如下,这种写法 组与层的索引皆从0开始
σ o ( s ) = σ 0 ⋅ 2 o + s S \sigma_{o}(s)= \sigma_0\cdot2^{o+\frac{s}{S}} σo(s)=σ0⋅2o+Ss
- σ 0 \sigma_0 σ0 为初始尺度(第0组 第0层 的尺度)
- o o o :组索引,从0开始
- s s s:层索引号, 从0开始
- S S S是金字塔每组的层数, S = i n t e r v a l + 3 = 6 S = interval +3 = 6 S=interval+3=6
(0 和 o 要看清楚哈)
举例: 构建一个一共N组,每组5的金字塔,初始尺度 σ 0 = 1.6 \sigma_0=1.6 σ0=1.6
| ( S = 5 ) (S=5) (S=5) | 第1组 | 第2组 | 第3组 | … |
|---|---|---|---|---|
| 第1层 | σ 0 ( 0 ) = 1.6 \sigma_0(0)=1.6 σ0(0)=1.6 | σ 1 ( 0 ) = σ 0 ( 0 ) ⋅ 2 = 3.2 \sigma_1(0)=\sigma_0(0)\cdot2=3.2 σ1(0)=σ0(0)⋅2=3.2 | σ 2 ( 0 ) = σ 1 ( 0 ) ⋅ 2 = 6.4 \sigma_2(0)=\sigma_1(0)\cdot2=6.4 σ2(0)=σ1(0)⋅2=6.4 | … |
| 第2层 | σ 0 ( 1 ) = σ 0 ( 0 ) ⋅ 2 1 / S = 1.838 \sigma_0(1)=\sigma_0(0)\cdot2^{1/S} = 1.838 σ0(1)=σ0(0)⋅21/S=1.838 | σ 1 ( 1 ) = σ 0 ( 1 ) ⋅ 2 = 3.676 \sigma_1(1)=\sigma_0(1)\cdot2=3.676 σ1(1)=σ0(1)⋅2=3.676 | σ 2 ( 1 ) = σ 1 ( 1 ) ⋅ 2 = 7.351 \sigma_2(1)=\sigma_1(1)\cdot2=7.351 σ2(1)=σ1(1)⋅2=7.351 | … |
| 第3层 | σ 0 ( 2 ) = σ 0 ( 0 ) ⋅ 2 2 / S = 2.111 \sigma_0(2)=\sigma_0(0)\cdot2^{2/S} =2.111 σ0(2)=σ0(0)⋅22/S=2.111 | σ 1 ( 2 ) = σ 0 ( 2 ) ⋅ 2 = 4.222 \sigma_1(2)=\sigma_0(2)\cdot2=4.222 σ1(2)=σ0(2)⋅2=4.222 | σ 2 ( 2 ) = σ 1 ( 2 ) ⋅ 2 = 8.445 \sigma_2(2)=\sigma_1(2)\cdot2=8.445 σ2(2)=σ1(2)⋅2=8.445 | … |
| 第4层 | σ 0 ( 3 ) = σ 0 ( 0 ) ⋅ 2 3 / S = 2.425 \sigma_0(3)=\sigma_0(0)\cdot2^{3/S} =2.425 σ0(3)=σ0(0)⋅23/S=2.425 | σ 1 ( 3 ) = σ 0 ( 3 ) ⋅ 2 = 4.850 \sigma_1(3)=\sigma_0(3)\cdot2=4.850 σ1(3)=σ0(3)⋅2=4.850 | σ 2 ( 3 ) = σ 1 ( 3 ) ⋅ 2 = 9.701 \sigma_2(3)=\sigma_1(3)\cdot2=9.701 σ2(3)=σ1(3)⋅2=9.701 | … |
| 第5层 | σ 0 ( 4 ) = σ 0 ( 0 ) ⋅ 2 4 / S = 2.786 \sigma_0(4)=\sigma_0(0)\cdot2^{4/S} =2.786 σ0(4)=σ0(0)⋅24/S=2.786 | σ 1 ( 4 ) = σ 0 ( 4 ) ⋅ 2 = 5.572 \sigma_1(4)=\sigma_0(4)\cdot2=5.572 σ1(4)=σ0(4)⋅2=5.572 | σ 2 ( 4 ) = σ 1 ( 4 ) ⋅ 2 = 11.14 \sigma_2(4)=\sigma_1(4)\cdot2=11.14 σ2(4)=σ1(4)⋅2=11.14 | … |
import numpy as np
octave =5
layer = 5
sigma0 = 1.6
space_scale = np.zeros((octave, layer))
for i in range(octave):
for j in range(layer):
sigma = sigma0 * 2 ** (i+j/layer)
space_scale[i, j] = sigma
print(space_scale)
# [[ 1.6 1.83791737 2.11121266 2.42514651 2.7857618 ]
# [ 3.2 3.67583474 4.22242531 4.85029301 5.57152361]
# [ 6.4 7.35166947 8.44485063 9.70058603 11.14304721]
# [12.8 14.70333894 16.88970126 19.40117205 22.28609442]
# [25.6 29.40667789 33.77940252 38.8023441 44.57218884]]
2)空间尺度的初始值 σ 0 \sigma_0 σ0
Lowe 在论文中,建议第0层的初始尺度为 σ 0 = 1.6 \sigma_0=1.6 σ0=1.6。但考虑到 当图像通过相机拍摄时, 相机的镜头已经对图像进行了一次 σ = 0.5 \sigma=0.5 σ=0.5 的初始的模糊,所以根据高斯模糊的性质,实际还需要模糊的尺度为:
σ 0 = σ i n i t × σ i n i t − σ p r e × σ p r e = 1.6 ∗ 1.6 − 0.5 ∗ 0.5 = 1.52 \sigma_0 = \sqrt{\sigma_{init} \times \sigma_{init} - \sigma_{pre} \times \sigma_{pre}} = \sqrt{1.6 * 1.6 - 0.5 * 0.5} = 1.52 σ0=σinit×σinit−σpre×σpre=1.6∗1.6−0.5∗0.5=1.52
高斯模糊性质:
对一副图像进行多次连续高斯模糊的效果与一次更大的高斯模糊可以产生同样的效果,大的高斯模糊的半径是所用多个高斯模糊半径平方和的平方根。例如,连续使用半径分别为 6 和 8 的两次高斯模糊变换得到的效果等同于使用一次半径为10的高斯模糊效果, 6 2 + 8 2 = 10 \sqrt{6^2+8^2}=10 62+82=10
证明过程
初始空间尺度 σ 0 \sigma_0 σ0是作用于base image上的,即 base image 的空间尺度为 σ = 1.6 \sigma=1.6 σ=1.6
def generateBaseImage(image, sigma, assumed_blur):
"""
Generate base image from input image by upsampling by 2 in both directions and blurring
"""
image = resize(image, (0, 0), fx=2, fy=2, interpolation=INTER_LINEAR)
sigma_diff = sqrt(max((sigma ** 2) - ((2 * assumed_blur) ** 2), 0.01))
return GaussianBlur(image, (0, 0), sigmaX=sigma_diff, sigmaY=sigma_diff)
original_img = cv2.imread("image.png", cv2.IMREAD_GRAYSCALE)
image = original_img.astype('float32')
base_image = generateBaseImage(image, sigma=1.6, assumed_blur=0.5)
二、关键点的检测
- 目的:检测关键点(特征点)。关键点就是与周围像素灰度值差异较大的点,一般为边缘点或角点。
- 1994年,Lindeberg 研究发现,尺度归一化的LoG( σ 2 ∇ 2 G \sigma^2\nabla^2G σ2∇2G)与 DoG 极为相似。
- 2002年,Mikolajczyk 在详细的实验比较中发现 尺度归一化的高斯拉普拉斯函数( σ 2 ∇ 2 G \sigma^2\nabla^2 G σ2∇2G)的极大值和极小值 同其它的特征提取函数(例如:Gradient,Hessian,Harris角特征,等)比较,能够产生最稳定的图像特征。
- 作者思路:既然尺度归一化的高斯拉普拉斯函数( σ 2 ∇ 2 G \sigma^2\nabla^2G σ2∇2G)的极大值和极小值能产生稳定的图像特征点,那就用它来检测特征点吧,但是它对噪声太敏感了,那就在这之前先做个高斯模糊吧(Gaussian Blur ),这就有了 LoG(Laplacian of Gaussian)。奈何 LoG 计算量太大,恰好发DoG的结果与LoG的结果极为相似,计算还超简单。所以,那就用 DoG 来近似 LoG 吧。
所以,我们要做的,就是在DoG中找到极大值和极小值,作为关键点的候选
1、LoG(Laplacian of Gaussian)与 DoG(Difference of gaussian)
1)Laplacian 的定义
拉普拉斯变换运算:就是对原图像的 x方向 和 y方向,分别求 2阶偏导数,然后相加
L a p l a c i a n = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 Laplacian = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} Laplacian=∂x2∂2f+∂y2∂2f
2)LoG 的定义 (Laplacian of Gaussian)
上面说了,尺度归一化的高斯拉普拉斯函数( σ 2 ∇ 2 G \sigma^2\nabla^2 G σ2∇2G)的极大值和极小值能够产生极为稳定的图像特征点,然而它对噪声比较敏感,所以在做拉普拉斯变换之前,先做一个高斯模糊: ∇ 2 ( G ( x , y , σ ) ∗ I ( x , y ) ) \nabla ^2 ( G_{(x, y, \sigma)} * I_{(x, y)}) ∇2(G(x,y,σ)∗I(x,y))
对图像先做 Gaussian Blur,再做Laplacian 变换, 等于对图像做LoG运算(即,先对高斯核做拉普拉斯变换,再与图像做卷积)
∇ 2 ( G ( x , y , σ ) ∗ I ( x , y ) ) = ∇ 2 G ( x , y , σ ) ∗ I ( x , y ) \nabla ^2 ( G_{(x, y, \sigma)} * I_{(x, y)}) = \nabla ^2 G_{(x, y, \sigma)} * I_{(x, y)} ∇2(G(x,y,σ)∗I(x,y))=∇2G(x,y,σ)∗I(x,y)
- I ( x , y ) I_{(x, y)} I(x,y) 是原图像
- G ( x , y , σ ) G_{(x, y, \sigma)} G(x,y,σ) 是高斯核
- 符号 ∗ * ∗ 表示卷积运算
- ∇ 2 \nabla^2 ∇2表示Laplacian运算
所以,LoG 的定义就是:对高斯核(Gaussian kernel) 做 Laplacian 运算
L o G = ∇ 2 G ( x , y , σ ) = ∂ 2 G ∂ x 2 + ∂ 2 G ∂ y 2 LoG= \nabla ^2 G_{(x, y, \sigma)}= \frac{\partial^2 G}{\partial x^2} + \frac{\partial^2 G}{\partial y^2} LoG=∇2G(x,y,σ)=∂x2∂2G+∂y2∂2G
3) 可用 DoG 近似 LoG
DoG(Difference of Gaussian)的定义为:一张图像的两个高斯模糊图像的插值
D ( x , y , σ ) = ( G ( x , y , k σ ) − G ( x , y , σ ) ) ∗ I ( x , y ) = G ( x , y , k σ ) ∗ I ( x , y ) − G ( x , y , σ ) ∗ I ( x , y ) = L ( x , y , k σ ) − L ( x , y , σ ) \begin{aligned}D_{(x, y, \sigma)} &= (G_{(x, y, k\sigma)} - G_{(x, y, \sigma)}) * I_{(x, y)}\\ &= G_{(x, y, k\sigma)}* I_{(x, y)} - G_{(x, y, \sigma)} * I_{(x, y)}\\ &= L_{(x, y, k\sigma)} - L_{(x, y, \sigma)} \end{aligned} D(x,y,σ)=(G(x,y,kσ)−G(x,y,σ))∗I(x,y)=G(x,y,kσ)∗I(x,y)−G(x,y,σ)∗I(x,y)=L(x,y,kσ)−L(x,y,σ)
Lowe 说,可以通过热扩散方程(heat diffusion equation)来理解 DoG 和 σ 2 ∇ 2 G \sigma^2\nabla^2G σ2∇2G 的关系。我没有去研究 热扩散方程,我从网上找到了另外一种证明方法,由于证明篇幅偏长,我另起一篇写啦,看这篇文章的第4部分:LoG 与 DoG
这里我只简述下结论 :
G ( x , y , k σ ) − G ( x , y , σ ) ≈ ( k − 1 ) σ 2 ∇ 2 G G(x, y, k\sigma) - G(x, y, \sigma) \approx (k-1)\sigma^2\nabla^2G G(x,y,kσ)−G(x,y,σ)≈(k−1)σ2∇2G
也就是
D o G ≈ σ 2 ( k − 1 ) L o G DoG \approx \sigma^2(k-1)LoG DoG≈σ2(k−1)LoG
这里 k是一个趋近于1的常数
然后贴张图大家看看有多近似,如下图,左边是两个高斯函数,这两个高斯函数相减的到右边图像中的DoG曲线,右边图是 DOG和LoG的对比

2、高斯差分金字塔(DOG:difference of gaussian)
差分金字塔的是在高斯金字塔的基础上操作的,其建立过程是:在高斯金子塔中的每组中相邻两层相减(按图中位置来说是 下一层减上一层,按照索引来说是下一层间去上一层)
def generateDoGImages(gaussian_images):
dog_images = []
for gaussian_images_in_octave in gaussian_images:
dog_images_in_octave = []
for first_image, second_image in zip(gaussian_images_in_octave, gaussian_images_in_octave[1:]):
dog_images_in_octave.append(cv2.subtract(second_image, first_image)) # ordinary subtraction will not work because the images are unsigned integers
dog_images.append(dog_images_in_octave)
return np.array(dog_images, dtype=object)
**计算DoG图像的时候,要记得先把原图像转换成 float32 的数据类型,不然原图像为 uint8 的情况下,两个图像相减的结果是无符号的 0~255 的整型,比如 100 - 200 =156。在转换为float32后,100.0 - 200.0 =-100. 。DoG 的数据类型需要是一个可为负数的浮点型。
3、在DOG中找极值点
-
DoG 图像中的极大值和极小值的检测是在当前检测点(在下图中x表示)的相邻的尺度图像中,当前点的 3x3x3的邻域中,用与其他的26个点(下图中绿色圆表示)对比DoG值,判断当前检测点是否为极值点
-
极值点的检测只在同一组中从第2层开始至倒数第2层中进行。组中的第1层DoG图像和最后一层DoG图像不参与极值点检测(仅作为第2层和倒数第2层的邻域参与了对比)
# 与邻域点对比,判断是否为极值点
def isPixelAnExtremum(first_subimage, second_subimage, third_subimage, threshold):
center_pixel_value = second_subimage[1, 1]
if np.abs(center_pixel_value) > threshold:
if center_pixel_value > 0:
return np.all(center_pixel_value >= first_subimage) and \
np.all(center_pixel_value >= third_subimage) and \
np.all(center_pixel_value >= second_subimage[0, :]) and \
np.all(center_pixel_value >= second_subimage[2, :]) and \
center_pixel_value >= second_subimage[1, 0] and \
center_pixel_value >= second_subimage[1, 2]
if center_pixel_value < 0:
return np.all(center_pixel_value <= first_subimage) and \
np.all(center_pixel_value <= third_subimage) and \
np.all(center_pixel_value <= second_subimage[0, :]) and \
np.all(center_pixel_value <= second_subimage[2, :]) and \
center_pixel_value <= second_subimage[1, 0] and \
center_pixel_value <= second_subimage[1, 2]
return False
for i in range(image_border_width, first_image.shape[0] - image_border_width): # 图像高度范围
for j in range(image_border_width, first_image.shape[1] - image_border_width): # 图像宽度范围
if isPixelAnExtremum(first_image[i-1:i+2, j-1:j+2], second_image[i-1:i+2, j-1:j+2], third_image[i-1:i+1, j-1:j+2], threshold): # 如果是极值点
# 拟合出关键点的精确位置(亚像素位置)
localization_result = localizeExtremumViaQuadraticFit(i, j, image_index + 1, octave_index,num_intervals,
dog_images_in_octave,sigma, contrast_threshold,
image_border_width)
4、 尺度连续性
这里补充说下尺度连续性,也补充解释下高斯金字塔的层数为什么是 interval+3
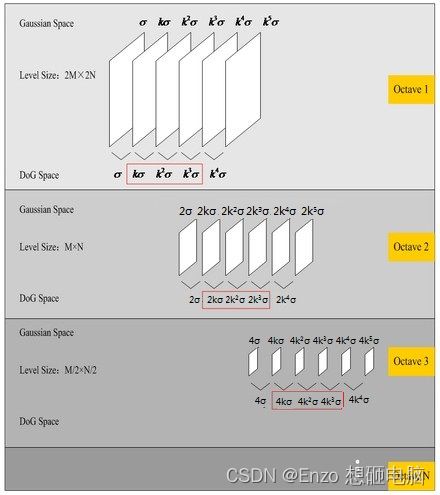
如上图,在 DoG Space中,每组的第1层和最后1层是不用来检测关键点的,所以只有红色框起来的层会用于检测关键点,我们希望用于检测关键点的层具有尺度连续性,也就是相邻层之间的尺度间隔为k倍,跨组间亦是如此。
所以,假设每组可用于关键点检测的层的图像数量是 interval =3 的情况下,就要求:
- 高斯差分金字塔 DoG 的每组层数量就是 interval + 2=5;
- 高斯金字塔(Gaussian pyramid) 的每组层数量就是 interval + 3 = 6
注:
interval =3,我们记为: n = 3 n=3 n=3
==>> k = 2 1 / n = 2 1 / 3 \quad k=2^{1/n}=2^{1/3}\quad k=21/n=21/3
==>> k 3 σ = 2 σ , 2 k 3 σ = 4 σ . . . \quad k^3\sigma=2\sigma, \quad 2k^3\sigma=4\sigma \quad... k3σ=2σ,2k3σ=4σ...
三、精确定位极值点
1、使用子像素插值法,根据 Taylor公式 拟合出精确的亚像素极值点
上面我们已经在 DoG空间中找到了极值点,但极值点在图像中的位置是离散的,离散空间的极值点并不是真正的极值点。下图显示了离散空间的极值点与连续空间极值点的差别。

为了提高关键点的稳定性与准确性,我们需要将之前已经提取出来的离散的关键点,通过对DoG尺度空进行曲线拟合,求得在连续空间中,关键点的精确的位置(位置坐标为float型),我们也成为亚像素。
这里我们用到的方法叫做 子像素插值法(Sub-pixel Interpolation),会使用到Taylor 公式的概念。
先来回顾一下 Taylor公式:
在二维空间中,如果有一个点 x 0 x_0 x0 接近于点 x x x,且函数 f f f 在 x x x点处可导,则可用 x 0 x_0 x0 的各阶导数值做系数构建一个多项式来近似表达 f ( x ) f_{(x)} f(x) 的值
Taylor 公式:
f ( x ) = f ( x 0 ) + f ( x 0 ) ′ ( x − x 0 ) + 1 2 f ( x 0 ) ′ ′ ( x − x 0 ) 2 + . . . + 1 n ! f ( x 0 ) n ( x − x 0 ) n f_{(x)}=f_{(x_0)}+f'_{(x_0)} (x-x_0)+ \frac{1}{2}f''_{(x_0)} (x-x_0)^2 + ...+\frac{1}{n!}f^{n}_{(x_0)} (x-x_0)^n f(x)=f(x0)+f(x0)′(x−x0)+21f(x0)′′(x−x0)2+...+n!1f(x0)n(x−x0)n
舍掉二阶以后的项,作为 f ( x ) f_{(x)} f(x) 的近似值:
f ( x ) ≈ f ( x 0 ) + f ( x 0 ) ′ ( x − x 0 ) + 1 2 f ( x 0 ) ′ ′ ( x − x 0 ) 2 f_{(x)} \approx f_{(x_0)}+f'_{(x_0)} (x-x_0)+ \frac{1}{2}f''_{(x_0)} (x-x_0)^2 f(x)≈f(x0)+f(x0)′(x−x0)+21f(x0)′′(x−x0)2
现在我们已知的是:
- DoG图像(DoG函数):对应的是函数 f f f;DoG中的每一个像素值对应的是 f ( x , y , σ ) f_{(x,y, \sigma)} f(x,y,σ)
- 关键点在离散空间的坐标: ( x 0 , y 0 , σ 0 ) (x_0, y_0,\sigma_0) (x0,y0,σ0)
**其实这里写 σ \sigma σ并不很准确,它指代的并不是真正的尺度 σ \sigma σ,而是组内的层索引 n n n,有点z轴的意思,是指在图片层级间的坐标,和真正的 σ \sigma σ 的计算关系为: σ = 2 n / i n t e r v a l \sigma = 2^{n/interval} σ=2n/interval。只是我查阅的资料都是用 σ \sigma σ 在表示,我也就这么写了吧,大家了解就好。
由已知可以求得的是:
- 关键点在D上的一阶导: ∂ D ∂ x 0 \frac{\partial D}{\partial x_0} ∂x0∂D、 ∂ D ∂ y 0 \frac{\partial D}{\partial y_0} ∂y0∂D、 ∂ D ∂ σ 0 \frac{\partial D}{\partial \sigma_0} ∂σ0∂D
- 关键点在D上的二阶导: ∂ 2 D ∂ x 0 2 \frac{\partial ^2 D}{\partial x_0^2} ∂x02∂2D、 ∂ 2 D ∂ y 0 2 \frac{\partial ^2 D}{\partial y_0^2} ∂y02∂2D、 ∂ 2 D ∂ σ 0 2 \frac{\partial ^2 D}{\partial \sigma_0^2} ∂σ02∂2D、 ∂ 2 D ∂ x 0 y 0 \frac{\partial ^2 D}{\partial x_0y_0} ∂x0y0∂2D、 ∂ 2 D ∂ x 0 σ 0 \frac{\partial ^2 D}{\partial x_0\sigma_0} ∂x0σ0∂2D、 ∂ 2 D ∂ y 0 σ 0 \frac{\partial ^2 D}{\partial y_0\sigma_0} ∂y0σ0∂2D
我们的目标是:求得连续空间中的极值点的坐标 ( x ^ , y ^ , σ ^ ) (\hat{x}, \hat{y}, \hat{\sigma}) (x^,y^,σ^)
======== 下面我们进行推导 ========
在DoG的四维空间中,Taylor 展开式为:
(四维分别为:关键点在x轴的位置,关键点在y轴的位置,关键点的尺度 σ \sigma σ,关键点的像素值 D ( x , y , σ ) D_{(x, y, \sigma)} D(x,y,σ))
f ( [ x , y , σ ] ) = f [ x 0 , y 0 , σ 0 ] + [ ∂ f ∂ x , ∂ f ∂ y , ∂ f ∂ σ ] ( [ x y σ ] − [ x 0 y 0 σ 0 ] ) + 1 2 ( [ x , y , σ ] − [ x 0 , y 0 , σ 0 ] ) [ ∂ 2 f ∂ x 2 ∂ 2 f ∂ x ∂ y ∂ 2 f ∂ x ∂ σ ∂ 2 f ∂ x ∂ y ∂ 2 f ∂ y 2 ∂ 2 f ∂ y ∂ σ ∂ 2 f ∂ x ∂ σ ∂ 2 f ∂ y ∂ σ ∂ 2 f ∂ σ 2 ] ( [ x y σ ] − [ x 0 y 0 σ 0 ] ) f_{([x, y, \sigma])} = f_{[x_0, y_0, \sigma_0]} + [\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial \sigma}]\left( \left [ \begin{array}{c} x\\ y\\ \sigma\\ \end{array} \right ]- \left [ \begin{array}{c} x_0\\ y_0\\ \sigma_0\\ \end{array} \right ] \right)+ \frac{1}{2}([x, y, \sigma]-[x_0, y_0, \sigma_0]) \left [ \begin{array}{c} \frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} & \frac{\partial^2 f}{\partial x \partial \sigma}\\\\ \frac{\partial^2 f}{\partial x \partial y} & \frac{\partial^2 f}{\partial y^2} & \frac{\partial^2 f}{\partial y \partial \sigma}\\\\ \frac{\partial^2 f}{\partial x \partial \sigma} & \frac{\partial^2 f}{\partial y \partial \sigma} & \frac{\partial^2 f}{\partial \sigma^2}\\\\ \end{array} \right ] \left( \left [ \begin{array}{c} x\\ y\\ \sigma\\ \end{array} \right ]- \left [ \begin{array}{c} x_0\\ y_0\\ \sigma_0\\ \end{array} \right ] \right) f([x,y,σ])=f[x0,y0,σ0]+[∂x∂f,∂y∂f,∂σ∂f]⎝⎛⎣⎡xyσ⎦⎤−⎣⎡x0y0σ0⎦⎤⎠⎞+21([x,y,σ]−[x0,y0,σ0])⎣⎢⎢⎢⎢⎢⎢⎢⎡∂x2∂2f∂x∂y∂2f∂x∂σ∂2f∂x∂y∂2f∂y2∂2f∂y∂σ∂2f∂x∂σ∂2f∂y∂σ∂2f∂σ2∂2f⎦⎥⎥⎥⎥⎥⎥⎥⎤⎝⎛⎣⎡xyσ⎦⎤−⎣⎡x0y0σ0⎦⎤⎠⎞
记 X = [ x y σ ] X = \left [ \begin{array}{c} x\\ y\\ \sigma\\ \end{array} \right ] X=⎣⎡xyσ⎦⎤, X 0 = [ x 0 y 0 σ 0 ] , D = f X_0 = \left [ \begin{array}{c} x_0\\ y_0\\ \sigma_0\\ \end{array} \right ],D =f X0=⎣⎡x0y0σ0⎦⎤,D=f,则公式简写为:
D ( X ) = D ( X 0 ) + ∂ D ∂ X 0 ( X − X 0 ) + 1 2 ∂ 2 D ∂ X 0 2 ( X − X 0 ) 2 D_{(X)} = D_{(X_0)} + \frac{\partial D}{\partial X_0}(X-X_0)+ \frac{1}{2} \frac{\partial ^2 D}{\partial X_0^2}(X-X_0)^2 D(X)=D(X0)+∂X0∂D(X−X0)+21∂X02∂2D(X−X0)2
因为我们打算 计算出真实极值点的坐标 距离离散极值点的距离,所以令 X 0 = 0 X_0=0 X0=0,得到的 X ^ \hat{X} X^ 就是偏移量。
D ( X ) = D ( X 0 ) + ∂ D ∂ X 0 X + 1 2 ∂ 2 D ∂ X 0 2 X 2 (1) D_{(X)} = D_{(X_0)} + \frac{\partial D}{\partial X_0}X+ \frac{1}{2} \frac{\partial ^2 D}{\partial X_0^2}X^2 \tag{1} D(X)=D(X0)+∂X0∂DX+21∂X02∂2DX2(1)
因为我们要找的点 X ^ \hat{X} X^点 是极值点,所以在 X ^ \hat{X} X^点处 ∂ D ∂ X = 0 \frac{\partial D}{\partial X}=0 ∂X∂D=0,用公式(1)对 X X X求导,并令方程等于0:
∂ D ∂ X 0 + ∂ 2 D ∂ X 0 2 X = 0 X ^ = − ( ∂ 2 D ∂ X 0 2 ) − 1 ∂ D ∂ X 0 (2) \frac{\partial D}{\partial X_0} + \frac{\partial^2 D}{\partial X_0^2} X =0 \\ \ \\ \hat{X} = - (\frac{\partial^2 D}{\partial X_0^2})^{-1} \frac{\partial D}{\partial X_0} \tag{2} ∂X0∂D+∂X02∂2DX=0 X^=−(∂X02∂2D)−1∂X0∂D(2)
其中:
∂ D ∂ X 0 = [ ∂ D ∂ x 0 , ∂ D ∂ y 0 , ∂ D ∂ σ 0 ] ∂ 2 D ∂ X 0 2 = [ ∂ 2 D ∂ x 2 ∂ 2 D ∂ x ∂ y ∂ 2 D ∂ x ∂ σ ∂ 2 D ∂ x ∂ y ∂ 2 D ∂ y 2 ∂ 2 D ∂ y ∂ σ ∂ 2 D ∂ x ∂ σ ∂ 2 D ∂ y ∂ σ ∂ 2 D ∂ σ 2 ] ∂ D x 0 = D ( x + 1 , y , σ ) − D ( x − 1 , y , σ ) 2 ∂ D y 0 = D ( x , y + 1 , σ ) − D ( x , y − 1 , σ ) 2 ∂ D σ 0 = D ( x , y , σ + 1 ) − D ( x , y , σ − 1 ) 2 ∂ 2 D x 0 2 = D ( x + 1 , y , σ ) − 2 D ( x , y , σ ) + D ( x − 1 , y , σ ) ∂ 2 D y 0 2 = D ( x , y + 1 , σ ) − 2 D ( x , y , σ ) + D ( x , y − 1 , σ ) ∂ 2 D σ 0 2 = D ( x , y , σ + 1 ) − 2 D ( x , y , σ ) + D ( x , y , σ ) ∂ 2 D x 0 y 0 = D ( x + 1 , y + 1 , σ ) − D ( x + 1 , y − 1 , σ ) − D ( x − 1 , y + 1 , σ ) + D ( x − 1 , y − 1 , σ ) 4 ∂ 2 D x 0 σ 0 = D ( x + 1 , y , σ + 1 ) − D ( x + 1 , y , σ − 1 ) − D ( x − 1 , y , σ + 1 ) + D ( x − 1 , y , σ − 1 ) 4 ∂ 2 D y 0 σ 0 = D ( x , y + 1 , σ + 1 ) − D ( x , y + 1 , σ − 1 ) − D ( x , y − 1 , σ + 1 ) + D ( x , y − 1 , σ − 1 ) 4 \frac{\partial D}{\partial X_0} = \left [ \frac{\partial D}{\partial x_0},\frac{\partial D}{\partial y_0} ,\frac{\partial D}{\partial \sigma_0} \right ] \\ \ \\ \frac{\partial^2 D}{\partial X_0^2} = \left [ \begin{array}{c} \frac{\partial^2 D}{\partial x^2} & \frac{\partial^2 D}{\partial x \partial y} & \frac{\partial^2 D}{\partial x \partial \sigma}\\\\ \frac{\partial^2 D}{\partial x \partial y} & \frac{\partial^2 D}{\partial y^2} & \frac{\partial^2 D}{\partial y \partial \sigma}\\\\ \frac{\partial^2 D}{\partial x \partial \sigma} & \frac{\partial^2 D}{\partial y \partial \sigma} & \frac{\partial^2 D}{\partial \sigma^2} \end{array} \right ] \\ \ \\ \frac{\partial D}{x_0} = \frac{D_{(x+1,y,\sigma)} - D_{(x-1,y,\sigma)}}{2} \\ \ \\ \frac{\partial D}{y_0} = \frac{D_{(x,y+1,\sigma)} - D_{(x,y-1,\sigma)}}{2} \\ \ \\ \frac{\partial D}{\sigma_0} = \frac{D_{(x,y,\sigma+1)} - D_{(x,y,\sigma-1)}}{2} \\ \ \\ \frac{\partial^2 D}{x_0^2} = D_{(x+1,y,\sigma)} - 2D_{(x,y,\sigma)} + D_{(x-1,y,\sigma)} \\ \ \\ \frac{\partial^2 D}{y_0^2} = D_{(x,y+1,\sigma)} - 2D_{(x,y,\sigma)} + D_{(x,y-1,\sigma)} \\ \ \\ \frac{\partial^2 D}{\sigma_0^2} = D_{(x,y,\sigma+1)} - 2D_{(x,y,\sigma)} + D_{(x,y,\sigma)} \\ \ \\ \frac{\partial^2 D}{x_0y_0} = \frac{D_{(x+1,y+1,\sigma)} - D_{(x+1,y-1,\sigma)} - D_{(x-1,y+1,\sigma)} + D_{(x-1,y-1,\sigma)}}{4} \\ \ \\ \frac{\partial^2 D}{x_0\sigma_0} = \frac{D_{(x+1,y,\sigma+1)} - D_{(x+1,y,\sigma-1)} - D_{(x-1,y,\sigma+1)} + D_{(x-1,y,\sigma-1)}}{4} \\ \ \\ \frac{\partial^2 D}{y_0\sigma_0} = \frac{D_{(x,y+1,\sigma+1)} - D_{(x,y+1,\sigma-1)} - D_{(x,y-1,\sigma+1)} + D_{(x,y-1,\sigma-1)}}{4} ∂X0∂D=[∂x0∂D,∂y0∂D,∂σ0∂D] ∂X02∂2D=⎣⎢⎢⎢⎢⎢⎡∂x2∂2D∂x∂y∂2D∂x∂σ∂2D∂x∂y∂2D∂y2∂2D∂y∂σ∂2D∂x∂σ∂2D∂y∂σ∂2D∂σ2∂2D⎦⎥⎥⎥⎥⎥⎤ x0∂D=2D(x+1,y,σ)−D(x−1,y,σ) y0∂D=2D(x,y+1,σ)−D(x,y−1,σ) σ0∂D=2D(x,y,σ+1)−D(x,y,σ−1) x02∂2D=D(x+1,y,σ)−2D(x,y,σ)+D(x−1,y,σ) y02∂2D=D(x,y+1,σ)−2D(x,y,σ)+D(x,y−1,σ) σ02∂2D=D(x,y,σ+1)−2D(x,y,σ)+D(x,y,σ) x0y0∂2D=4D(x+1,y+1,σ)−D(x+1,y−1,σ)−D(x−1,y+1,σ)+D(x−1,y−1,σ) x0σ0∂2D=4D(x+1,y,σ+1)−D(x+1,y,σ−1)−D(x−1,y,σ+1)+D(x−1,y,σ−1) y0σ0∂2D=4D(x,y+1,σ+1)−D(x,y+1,σ−1)−D(x,y−1,σ+1)+D(x,y−1,σ−1)
因为我们上面定义 X 0 = 0 X_0=0 X0=0,代表插值中心,所以, X ^ − X 0 = X ^ − 0 = X ^ \hat{X} - X_0 = \hat{X} - 0 =\hat{X} X^−X0=X^−0=X^ 就是相对插值中心的偏移量。
当它在任一维度上的偏移量大于0.5时,就意味着关键点已经偏移到它的邻近点上,所以必须更新关键点的位置。然后在新的位置上反复插值直到收敛(偏移量都小于0.5,不再需要更新);也有可能超出所设定的迭代次数仍未收敛,或者更新后的关键点位置超出了图像边界的范围,此时这样的点应该删除。Lowe 在论文中描述说,他在实验中设置的迭代次数为5。
另外,过小的点易受噪声的干扰而变得不稳定,所以将小于某个经验值(Lowe论文中使用0.03,rmislam实现时使用 threshold=0.04/interval)的极值点删除。
通过这部分的操作,我们可以获取特征点的精确位置 X ^ = ( x ^ , y ^ , σ ^ ) \hat{X}=(\hat{x}, \hat{y}, \hat{\sigma}) X^=(x^,y^,σ^)。
公式(2)带入公式(1),得极值点 X ^ \hat{X} X^ 处的像素值为:
D X ^ = D X 0 + 1 2 ∂ D ∂ X 0 X ^ D_{\hat{X}}=D_{X_0} + \frac{1}{2}\frac{\partial D}{\partial X_0}\hat{X} DX^=DX0+21∂X0∂DX^
2、消除边缘相应
我们希望找到的关键点是角点或者更有特征的点,而不是边缘点,因为边缘点不稳定。而 DoG算子会产较强的边缘响应(DoG 取极值点的时候很容易取到边缘点),所以我们要剔除不稳定的边缘点。
边缘点的特征为:垂直边缘的方向上,有较大的主曲率,而沿着边缘方向有较小的主曲率。
曲率, 即 弯曲程度。
直观来想, 以一条连续光滑曲线上无限接近的两个点为端点的一段弧总应该可以看作是某圆上的一段弧,而这个圆的半径就被定义为曲线在这一点的曲率半径,而曲率则被定义为曲率半径的倒数。
曲线弧度越大,曲率越大,曲线弧度越小,曲率越小
参考链接:点击查看
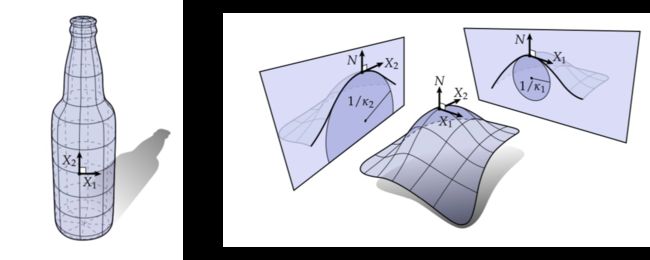
对于一个曲面,我们可以用跟曲线曲率一样的定义来看曲面上的某个方向的曲线的曲率,比如下图玻璃瓶上的这个点,在 X 1 X_1 X1方向它的曲率是 1/R,而在 X 2 X_2 X2方向上则它的曲率是是0.
如下图右图,在曲面上取一点E,曲面在E点的法线为N轴,过N轴可以有无限多个剖切平面,每个剖切平面与曲面相交,其交线为一条平面曲线,每条平面曲线在E点有一个曲率半径。不同的剖切平面上的平面曲线在E点的曲率半径一般是不相等的。这些曲率半径中,有一个最大和最小的曲率半径,称之为主曲率半径,记作 k1 与 k2,这两个曲率半径所在的方向,数学上可以证明是相互垂直的。参考链接:点击查看
重点是:该点的Hessian matrix 的特征值 对应的是该点的主曲率
获取特征点处的Hessian矩阵: H = [ ∂ 2 D ∂ x 2 ∂ 2 D ∂ x ∂ y ∂ 2 D ∂ x ∂ y ∂ 2 D ∂ y 2 ] H=\left [ \begin{array}{c} \frac{\partial^2 D}{\partial x^2} & \frac{\partial^2 D}{\partial x \partial y}\\\\ \frac{\partial^2 D}{\partial x \partial y} & \frac{\partial^2 D}{\partial y^2} \end{array} \right ] H=⎣⎢⎡∂x2∂2D∂x∂y∂2D∂x∂y∂2D∂y2∂2D⎦⎥⎤
假设 关键点在 x方向 和 y方向 的主曲率分别为 α 和 β \alpha 和 \beta α和β( α ≥ β \alpha \geq \beta α≥β),则 H H H 的特征值也为 α 和 β \alpha 和 \beta α和β
根据矩阵的特征点的性质:
- 矩阵A的行列式的值为所有特征值的积
- 矩阵A的对角线元素和(称为A的迹)等于特征值的和
T h ( H ) 为 H 的 对 角 元 素 和 : T h ( H ) = ∂ 2 D ∂ x 2 + ∂ 2 D ∂ y 2 = α + β D e t ( H ) 为 H 的 行 列 式 的 值 : D e t ( H ) = ∂ 2 D ∂ x 2 ∂ 2 D ∂ y 2 − ( ∂ 2 D ∂ x ∂ y ) 2 = α β Th(H)为H的对角元素和:Th(H) = \frac{\partial^2 D}{\partial x^2} + \frac{\partial^2 D}{\partial y^2} = \alpha + \beta \\ \ \\ Det(H)为H的行列式的值:Det(H) = \frac{\partial^2 D}{\partial x^2} \frac{\partial^2 D}{\partial y^2} - (\frac{\partial^2 D}{\partial x \partial y})^2 = \alpha \beta Th(H)为H的对角元素和:Th(H)=∂x2∂2D+∂y2∂2D=α+β Det(H)为H的行列式的值:Det(H)=∂x2∂2D∂y2∂2D−(∂x∂y∂2D)2=αβ
为了避免直接计算特征值(主曲率值),而只是考虑他们之间的比率,我们令 r = α β r= \frac{\alpha}{\beta} r=βα , ( r ≥ 1 r\geq1 r≥1),则有:
T r ( H ) 2 D e t ( H ) = ( α + β ) 2 α β = ( r β + β ) 2 r β 2 = ( r + 1 ) 2 r \frac{Tr(H)^2}{Det(H)} = \frac{(\alpha + \beta)^2}{\alpha\beta} = \frac{(r\beta + \beta)^2}{r\beta^2} = \frac{(r+1)^2}{r} Det(H)Tr(H)2=αβ(α+β)2=rβ2(rβ+β)2=r(r+1)2
当两个特征值相等时(即 r = 1 r=1 r=1时),公式 ( r + 1 ) 2 r \frac{(r+1)^2}{r} r(r+1)2的值最小,且随着 r r r值的增大而增大。 r r r值越大,说明两个特征值的比值越大,即在某一个方向的梯度值越大,而在另一个方向的梯度值越小,而边缘恰恰就是这种情况。所以为了剔除边缘响应点,需要让该比值小于一定的阈值。因此,为了检测主曲率是否在某域值 r t h r e s h o l d r_{threshold} rthreshold下,只需检测:
T r ( H ) 2 D e t ( H ) < ( r t h r e s h o l d + 1 ) 2 r t h r e s h o l d \frac{Tr(H)^2}{Det(H)} < \frac{(r_{threshold}+1)^2}{r_{threshold}} Det(H)Tr(H)2<rthreshold(rthreshold+1)2
Lowe 论文中建议 r t h r e s h o l d = 10 r_{threshold}=10 rthreshold=10, Opencv 中也采用的 r t h r e s h o l d = 10 r_{threshold}=10 rthreshold=10
localization_result = localizeExtremumViaQuadraticFit(i, j, image_index + 1, octave_index,
num_intervals, dog_images_in_octave,
sigma, contrast_threshold, image_border_width)
def localizeExtremumViaQuadraticFit(i, j, image_index, octave_index, num_intervals, dog_images_in_octave, sigma, contrast_threshold, image_border_width, eigenvalue_ratio=10, num_attempts_until_convergence=5):
logger.debug('Localizing scale-space extrema...')
extremum_is_outside_image = False
image_shape = dog_images_in_octave[0].shape
for attempt_index in range(num_attempts_until_convergence):
# need to convert from uint8 to float32 to compute derivatives and need to rescale pixel values to [0, 1] to apply Lowe's thresholds
first_image, second_image, third_image = dog_images_in_octave[image_index-1:image_index+2]
pixel_cube = np.stack([first_image[i-1:i+2, j-1:j+2],
second_image[i-1:i+2, j-1:j+2],
third_image[i-1:i+2, j-1:j+2]]).astype('float32') / 255.
gradient = computeGradientAtCenterPixel(pixel_cube)
hessian = computeHessianAtCenterPixel(pixel_cube)
extremum_update = -np.linalg.lstsq(hessian, gradient, rcond=None)[0]
if abs(extremum_update[0]) < 0.5 and abs(extremum_update[1]) < 0.5 and abs(extremum_update[2]) < 0.5:
break
j += int(round(extremum_update[0]))
i += int(round(extremum_update[1]))
image_index += int(round(extremum_update[2]))
# make sure the new pixel_cube will lie entirely within the image
if i < image_border_width or i >= image_shape[0] - image_border_width or j < image_border_width or j >= image_shape[1] - image_border_width or image_index < 1 or image_index > num_intervals:
extremum_is_outside_image = True
break
if extremum_is_outside_image:
logger.debug('Updated extremum moved outside of image before reaching convergence. Skipping...')
return None
if attempt_index >= num_attempts_until_convergence - 1:
logger.debug('Exceeded maximum number of attempts without reaching convergence for this extremum. Skipping...')
return None
functionValueAtUpdatedExtremum = pixel_cube[1, 1, 1] + 0.5 * np.dot(gradient, extremum_update)
if abs(functionValueAtUpdatedExtremum) * num_intervals >= contrast_threshold:
xy_hessian = hessian[:2, :2]
xy_hessian_trace = np.trace(xy_hessian)
xy_hessian_det = np.linalg.det(xy_hessian)
if xy_hessian_det > 0 and eigenvalue_ratio * (xy_hessian_trace ** 2) < ((eigenvalue_ratio + 1) ** 2) * xy_hessian_det:
# Contrast check passed -- construct and return OpenCV KeyPoint object
keypoint = cv2.KeyPoint()
keypoint.pt = ((j + extremum_update[0]) * (2 ** octave_index), (i + extremum_update[1]) * (2 ** octave_index))
keypoint.octave = octave_index + image_index * (2 ** 8) + int(round((extremum_update[2] + 0.5) * 255)) * (2 ** 16)
keypoint.size = sigma * (2 ** ((image_index + extremum_update[2]) / np.float32(num_intervals))) * (2 ** (octave_index + 1)) # octave_index + 1 because the input image was doubled
keypoint.response = abs(functionValueAtUpdatedExtremum)
return keypoint, image_index
return None
def computeGradientAtCenterPixel(pixel_array):
dx = 0.5 * (pixel_array[1, 1, 2] - pixel_array[1, 1, 0])
dy = 0.5 * (pixel_array[1, 2, 1] - pixel_array[1, 0, 1])
ds = 0.5 * (pixel_array[2, 1, 1] - pixel_array[0, 1, 1])
return np.array([dx, dy, ds])
def computeHessianAtCenterPixel(pixel_array):
center_pixel_value = pixel_array[1, 1, 1]
dxx = pixel_array[1, 1, 2] - 2 * center_pixel_value + pixel_array[1, 1, 0]
dyy = pixel_array[1, 2, 1] - 2 * center_pixel_value + pixel_array[1, 0, 1]
dss = pixel_array[2, 1, 1] - 2 * center_pixel_value + pixel_array[0, 1, 1]
dxy = 0.25 * (pixel_array[1, 2, 2] - pixel_array[1, 2, 0] - pixel_array[1, 0, 2] + pixel_array[1, 0, 0])
dxs = 0.25 * (pixel_array[2, 1, 2] - pixel_array[2, 1, 0] - pixel_array[0, 1, 2] + pixel_array[0, 1, 0])
dys = 0.25 * (pixel_array[2, 2, 1] - pixel_array[2, 0, 1] - pixel_array[0, 2, 1] + pixel_array[0, 0, 1])
return np.array([[dxx, dxy, dxs],
[dxy, dyy, dys],
[dxs, dys, dss]])
四、关键点方向分配
-
目的:为了使描述符具有旋转不变性,我们利用图像的局部特征给每一个关键点分配一个基准方向。
-
方法:对于在DOG金字塔中检测出的关键点,计算其所在高斯金字塔图像中 3σ邻域窗口内,每个像素的梯度和方向。再做直方图统计,取最大值的那个方向作为关键点的基准方向。
1、3σ邻域窗口
按Lowe的建议,梯度的模值m(x,y)按 σ = 1.5 σ o c t \sigma=1.5\sigma_{oct} σ=1.5σoct的高斯分布加成,按尺度采样的3σ原则,邻域窗口半径为 3 ∗ 1.5 σ o c t 3 *1.5\sigma_{oct} 3∗1.5σoct。
那 σ o c t \sigma_{oct} σoct 的取值是什么? 还记得我们上面【三、精确定位极值点】求得的 X ^ = [ x ^ , y ^ , σ ^ ] \hat{X}=[\hat{x}, \hat{y}, \hat{\sigma}] X^=[x^,y^,σ^] 嘛? 当时说了这么一句话:
其实这里写 σ \sigma σ并不很准确,它指代的并不是真正的尺度 σ \sigma σ,而是组内的层索引 n n n,有点z轴的意思,是指在图片层级间的坐标,它和真正的 σ \sigma σ 的计算关系为: σ = 2 n / i n t e r v a l \sigma = 2^{n/interval} σ=2n/interval。只是我查阅的资料都是用 σ \sigma σ 在表示,我也就这么写了吧,大家了解就好。
所以, σ ^ \hat{\sigma} σ^指的是关键点在图像层级坐标的中偏移量,我们这里换个写法,记为 Δ i \Delta i Δi ,( Δ i m a g e _ i n d e x \Delta image\_index Δimage_index 的意思)
所以: σ o c t = 2 o + ( i + Δ i ) i n t e r v a l \sigma_{oct} = 2^{o + \frac{ (i + \Delta i)}{interval}} σoct=2o+interval(i+Δi),其中, o o o为组索引, i i i为层索引, Δ i \Delta i Δi 为层索引偏移量
scale_factor = 1.5
radius_factor = 3
scale = sigma * (2 ** ((image_index + extremum_update[2]) / float32(num_intervals))) # 当前关键点所在的尺度 σ_oct
radius = int(round(radius_factor * scale_factor * scale))
2、关键点的梯度值 与 梯度方向
- 计算公式:
-
梯 度 的 模 值 : m ( x , y ) = ( L ( x + 1 , y ) − L ( x − 1 , y ) ) 2 + ( L ( x , y + 1 ) − L ( x , y − 1 ) ) 2 梯度的模值:m_{(x, y)} = \sqrt{(L(x+1,y)-L(x-1,y))^2 + (L(x, y+1)-L(x,y-1))^2} 梯度的模值:m(x,y)=(L(x+1,y)−L(x−1,y))2+(L(x,y+1)−L(x,y−1))2
-
梯 度 的 方 向 : θ ( x , y ) = t a n − 1 L ( x , y + 1 ) − L ( x , y − 1 ) L ( x + 1 , y ) − L ( x − 1 , y ) 梯度的方向:\theta_{(x, y)} = tan^{-1}\frac{L(x, y+1)-L(x,y-1)}{L(x+1,y)-L(x-1,y)} 梯度的方向:θ(x,y)=tan−1L(x+1,y)−L(x−1,y)L(x,y+1)−L(x,y−1)
-
dx = (gaussian_image[region_y, region_x + 1] - gaussian_image[region_y, region_x - 1]).astype(np.float)
dy = (gaussian_image[region_y - 1, region_x] - gaussian_image[region_y + 1, region_x]).astype(np.float)
gradient_magnitude = np.sqrt(dx * dx + dy * dy)
gradient_orientation = np.rad2deg(np.arctan2(dy, dx))
3、梯度直方图
在完成关键点邻域内所有的像素点的梯度计算后,使用直方图统计邻域内像素的梯度值和方向。
梯度直方图将0~360度的方向范围分为36个柱(bins),其中每柱10度。
梯度值不是直接累加到直方图中去的,需要乘以一个高斯权重:
w ( x , y ) = m ( x , y ) ∗ G ( x , y , 1.5 σ o c t ) w_{(x, y)} = m_{(x, y)} * G_{(x, y, 1.5\sigma_{oct})} w(x,y)=m(x,y)∗G(x,y,1.5σoct)
其中, σ o c t = 2 o + ( i + Δ i ) i n t e r v a l \sigma_{oct} = 2^{o + \frac{ (i + \Delta i)}{interval}} σoct=2o+interval(i+Δi), G ( x , y , 1.5 σ o c t ) = e x 2 + y 2 2 σ 2 G_{(x, y, 1.5\sigma_{oct})} = e^{\frac{x^2+y^2}{2\sigma^2}} G(x,y,1.5σoct)=e2σ2x2+y2,高斯权重的常数项系数可省略
# 梯度值 和 梯度方向
gradient_magnitude = np.sqrt(dx * dx + dy * dy) # 梯度值
gradient_orientation = np.rad2deg(np.arctan2(dy, dx)) # 梯度方向
# 计算梯度权重,extremum_update[2] 是精确定位极值点时,拟合出的尺度偏移量
scale = sigma * (2 ** ((image_index + extremum_update[2]) / float32(num_intervals))) # 当前关键点所在的尺度 σ_oct
scale = scale_factor * scale # 尺度乘以系数 scale_factor = 1.5
weight = exp(- 0.5 * (i ** 2 + j ** 2) / (scale ** 2)) # 计算梯度权重,高斯函数的常数项可以省略
# 统计直方图
histogram_index = int(round(gradient_orientation * num_bins / 360.))
raw_histogram[histogram_index % num_bins] += weight * gradient_magnitude # 梯度值乘以高斯权重
如图下图所示,为初步统计的直方图(为简化,图中只画了八个方向的直方图),后续会对其做一个平滑处理
4、梯度直方图的平滑处理
为了防止某个梯度方向角度因受到噪声的干扰而突变,我们还需要对梯度方向直方图进行平滑处理。
Opencv 所使用的平滑公式如下,其中, i ∈ [ 0 , 35 ] i∈[0,35] i∈[0,35], h h h 和 H H H 分别表示平滑前和平滑后的直方图
H ( i ) = h ( i − 2 ) + h ( i + 2 ) 16 + 4 ( h ( i − 1 ) + h ( i + 1 ) ) 16 + 6 h ( i ) 16 H(i) = \frac{h_{(i-2)} + h_{(i+2)}}{16} + \frac{4(h_{(i-1)} + h_{(i+1)})}{16} + \frac{6h_{(i)}}{16} H(i)=16h(i−2)+h(i+2)+164(h(i−1)+h(i+1))+166h(i)
也就是说平滑的权重是这么分配的:
| 位置 | i − 2 i-2 i−2 | i − 1 i-1 i−1 | i i i | i + 1 i+1 i+1 | i + 2 i+2 i+2 |
|---|---|---|---|---|---|
| 权重 | 1 16 \frac{1}{16} 161 | 4 16 \frac{4}{16} 164 | 6 16 \frac{6}{16} 166 | 4 16 \frac{4}{16} 164 | 1 16 \frac{1}{16} 161 |
由于角度是循环的,即 0 ∘ = 36 0 ∘ 0^{\circ}=360^{\circ} 0∘=360∘,如果 i + 1 或 i + 2 i+1 或 i+2 i+1或i+2 超出了 [0,…,35] 的范围,那么可以通过圆周循环的方法找到它所对应的在 0 ~ 35 0 ~35 0~35 之间的值,如 h ( 36 ) = h ( 1 ) h_{(36)} = h_{(1)} h(36)=h(1)。
for n in range(num_bins):
smooth_histogram[n] = (6 * raw_histogram[n] + 4 * (raw_histogram[n - 1] + raw_histogram[(n + 1) % num_bins]) + raw_histogram[n - 2] + raw_histogram[(n + 2) % num_bins]) / 16.
5、关键点的 主方向 和 辅方向
-
取方向直方图中最大值作为该关键点的主方向
-
取方向直方图中的峰值作为该关键点处的辅方向,(峰值的定义为,比左右相邻的两个方向值都大,上图中就有3个峰值,分别为第2, 5, 8个)。为了增强匹配的鲁棒性,只保留峰值大于主方向峰值 80%的方向作为该关键点的辅方向。对于提取出的多个辅方向,我们同样作为关键点的信息进行记录,记录方式为使用关键点的位置和尺度,以及辅方向的方向。
-
离散的梯度方向直方图要进行插值拟合处理,来求得更精确的方向角度值
至此,我们已经检测出了含有位置、尺度和方向的关键点,这即是该图像的SIFT特征点。
五、关键点的特征描述
通过以上步骤,对于每一个关键点,拥有三个信息:位置、尺度以及方向。接下来就是为每个关键点建立一个描述符,用一组向量将这个关键点描述出来,使其不随各种变化而改变,比如光照变化、视角变化等等。这个描述子不但包括关键点,也包含关键点周围对其有贡献的像素点,并且描述符应该有较高的独特性,以便于提高特征点正确匹配的概率。
SIFT描述子是关键点邻域高斯图像梯度统计结果的一种表示。通过对关键点周围图像区域分块,计算块内梯度直方图,生成具有独特性的向量,这个向量是该区域图像信息的一种抽象,具有唯一性。
Lowe的实验中,关键点的邻域窗口中大小为 16 ∗ 16 16*16 16∗16 ,每 4 ∗ 4 4*4 4∗4 是一个subregion,从每个subregion中提取出一个descriptor,一共有16个descriptors。采用8个梯度方向,所以,descriptors 会用 16*8=128 维向量表征。
下图仅做示例,与Lowe的实验参数不一样。下图的邻域窗口为 8 ∗ 8 8*8 8∗8,每 4 ∗ 4 4*4 4∗4 是一个subregion,会生成32维向量的描述子。
1. 确定计算描述子所需的图像区域
特征描述子与特征点所在的尺度有关,因此,对梯度的求取应在特征点对应的高斯图像上进行。将关键点附近的 16 ∗ 16 16*16 16∗16 的邻域划分为 4 ∗ 4 4*4 4∗4个子区域,每个子区域的大小为 4 ∗ 4 4*4 4∗4,每个子区域做为一个种子点,每个种子点有8个方向。
每个子区域的大小与关键点方向分配时相同,即每个区域有个子像素,为每个子区域分配边长为的矩形区域进行采样(个子像素实际用边长为的矩形区域即可包含,但由式(3-8),不大,为了简化计算取其边长为,并且采样点宜多不宜少)。考虑到实际计算时,需要采用双线性插值,所需图像窗口边长为。在考虑到旋转因素(方便下一步将坐标轴旋转到关键点的方向),如下图6.1所示,实际计算所需的图像区域半径为:
【待补充,我写不下去了 】
六、总结
SIFT在图像的不变特征提取方面拥有无与伦比的优势,但并不完美,仍然存在:
-
实时性不高。
-
有时特征点较少。
-
对边缘光滑的目标无法准确提取特征点。
我真的尽力了,写不动了,厄!
如果觉得这片文章对你有用,就请收藏关注吧。
附:
1、图像的高频信息和低频信息:
低频信息:代表着图像中亮度或者灰度值变化缓慢的区域,也就是图像中大片平坦的区域,描述了图像的主要部分,是对整幅图像强度的综合度量。
高频信息:对应着图像变化剧烈的部分,也就是图像的边缘(轮廓)或者噪声以及细节部分。 另外,噪声(或噪点)因为它与周围像素点灰度值明显不一样,也就是灰度有快速地变化了,所以,噪声也是高频信息。
2、一个500*500的图片能提取出2000个稳定的特征点(虽然这个数据基于图像内容 以及参数选择)
Reference:
1、https://blog.csdn.net/zddblog/article/details/7521424
2、https://blog.csdn.net/lingyunxianhe/article/details/79063547