《深度学习进阶 自然语言处理》第六章:LSTM介绍
文章目录
-
-
- 6.1 RNN的问题
-
- 6.1.1 RNN的复习
- 6.1.2 梯度消失和梯度爆炸
- 6.1.4 梯度爆炸的对策
- 6.2 梯度消失和LSTM
-
- 6.2.1 LSTM的接口
- 6.2.2 LSTM层的结构
- 6.2.3 输出门
- 6.2.4 遗忘门
- 6.2.5 新的记忆单元
- 6.2.6 输入门
- 6.2.7 LSTM的梯度的流动
- 6.3 使用LSTM的语言模型
-
- 6.3.1 LSTM层的多层化
- 6.3.2 基于Dropout抑制过拟合
- 6.3.3 权重共享
- 6.4 总结
-
之前文章链接:
开篇介绍:《深度学习进阶 自然语言处理》书籍介绍
第一章:《深度学习进阶 自然语言处理》第一章:神经网络的复习
第二章:《深度学习进阶 自然语言处理》第二章:自然语言和单词的分布式表示
第三章:《深度学习进阶 自然语言处理》第三章:word2vec
第四章:《深度学习进阶 自然语言处理》第四章:Embedding层和负采样介绍
第五章:《深度学习进阶 自然语言处理》第五章:RNN通俗介绍
上一章我们介绍了结构比较简单的RNN,存在环路的RNN可以记忆过去的信息,只是效果不好,因为很多情况下它都无法很好地学习到时序数据的长期依赖关系。为了学习到时序数据的长期依赖关系,我们增加了一种名为“门”的结构,具有代表性的有LSTM和GRU等“Gated RNN”。本章将指出上一章的RNN问题,重点介绍LSTM的结构,并揭示它实现“长期记忆”的机制。
6.1 RNN的问题
上一章的RNN不擅长学习时序数据的长期依赖关系,是因为BPTT会发生梯消失和梯度爆炸的问题。本节先回顾一下上一章介绍的RNN层,并通过实例来说明为什么不擅长长期记忆。
6.1.1 RNN的复习
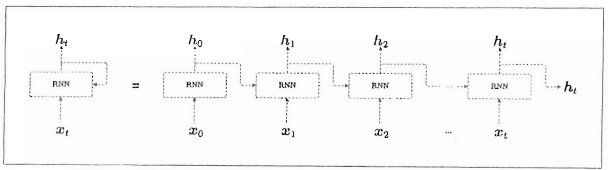
RNN层存在环路,展开来看它是一个在水平方向上延伸的网络,如下图
x t x_{t} xt是输入的时序数据, h t h_{t} ht是输出的隐藏状态,记录过去信息。RNN正是使用了上一刻的隐藏状态所以才可以继承过去的信息。RNN层的处理用计算图来表示的话,如下图:
如上图所示,RNN层的正向传播进行的计算包含矩阵乘积、矩阵加法和基于激活函数tanh的变换。这是我们上一章介绍的RNN层,下面我们看一下这其中存在的问题,主要是关于长期记忆的问题。
6.1.2 梯度消失和梯度爆炸
语言模型的任务是根据已经出现的单词预测下一个将要出现的单词。RNN层通过向过去传递“有意义的梯度”,理论上是能够学习时间方向上的依赖关系。但是随着时间的回溯,这个梯度在中途不可避免的变小(梯度消失)或者变大(梯度爆炸),权重参数不能正常更新,RNN层也就无法学习长期的依赖关系。
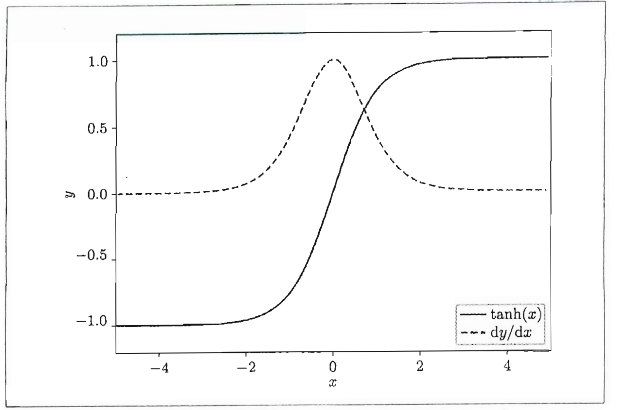
根据上一节的第二张图展示的RNN层正向传播的计算,可知反向传播的梯度依次流经tanh、矩阵加和(“+”)和MatMul(矩阵乘积)运算。"+"的反向传播梯度值不变。当y = tanh(x)时,它的导数是 d y d x = 1 − y 2 \frac{dy}{dx} = 1- y^{2} dxdy=1−y2,分别画在图上如下图:
图中的虚线可以看出,tanh(x)导数的值小于1.0,随着x远离0,它的值变小。这意味着,反向传播的梯度经过tanh节点时,它的值会越来越小。
接着我们看一下MatMul(矩阵乘积)节点,简单起见,我忽略tanh节点,这样RNN层的反向传播的梯度仅取决于矩阵乘积运算。通过下面代码来观察梯度大小的变化。
import numpy as np
import matplotlib.pyplot as plt
N = 2 # mini-batch的大小
H = 3 # 隐藏状态向量的维数
T = 20 # 时序数据的长度
dh = np.ones((N, H))
# np.random.seed(6) # 为了复现,固定随机数种子
Wh = np.random.randn(H, H)
norm_list = []
for t in range(T):
dh = np.dot(dh, Wh.T)
norm = np.sqrt(np.sum(dh**2)) / N
norm_list.append(norm)
print(norm_list)
多运行几次上面的代码可以发现,梯度的大小(norm值)随时间步长呈指数级增加/减小。为什么会出现这样的指数级变化呢?因为矩阵Wh被反复乘了T次。如果Wh是标量,当Wh大于1或小于1时,梯度呈指数级变化。但是Wh是矩阵,此时矩阵的奇异值作为指标。如果奇异值的最大值大于1,梯度可能呈指数级增加(必要非充分条件),最大值小于1,可以判断梯度会呈指数级减小。
6.1.4 梯度爆炸的对策
解决梯度爆炸有既定的方法,称为梯度裁剪(gradients clipping)。伪代码如下:
i f ∣ ∣ g ^ ∣ ∣ ≥ t h r e s h o l d : g ^ = t h r e s h o l d ∣ ∣ g ^ ∣ ∣ g ^ if \quad ||\hat{g}|| \geq threshold:\\ \hat{g} = \frac{threshold}{||\hat{g}||}\hat{g} if∣∣g^∣∣≥threshold:g^=∣∣g^∣∣thresholdg^
这里假设将神经网络用到的所有参数的梯度整合成一个,并用符号 g ^ \hat{g} g^表示,阈值设为threshold。当梯度的L2范数 ∣ ∣ g ^ ∣ ∣ ||\hat{g}|| ∣∣g^∣∣大于或等于阈值,就按照上面的方法修正梯度,这就是梯度裁剪。
6.2 梯度消失和LSTM
为了解决RNN的梯度消失问题,人们提出了诸多Gated RNN框架,具有代表性的有LSTM和GRU,本节我们只关注LSTM,从结构入手,阐明它为何不会引起梯度消失。
6.2.1 LSTM的接口
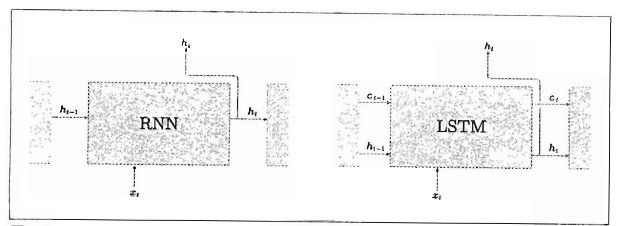
我们先以简略图比较一下LSTM与RNN的接口:
LSTM比RNN的接口多了一个路径c,这个c称为记忆单元,是LSTM专用的记忆部门,其特点是仅在LSTM层内部接收和传递数据,不向其他层输出。
6.2.2 LSTM层的结构
c t c_{t} ct存储了时刻t时LSTM的记忆,可以认为其中保存了过去到时刻t的所有必要信息,基于 c t c_{t} ct向外部输出隐藏状态 h t h_{t} ht。二者的关系是 h t h_{t} ht是 c t c_{t} ct经过tanh函数变换后的记忆单元, c t c_{t} ct和 h t h_{t} ht是按元素应用tanh函数,所以它们的元素个数相同。
进入下一项之前,我们需要特别说明的是,LSTM的门控并非只能“开/合“,还能通过”开合程度“来控制信息的流量。sigmoid函数的输出范围是0.0 ~ 1.0,所以用于求门的开合程度。
6.2.3 输出门
刚才介绍 h t h_{t} ht和 c t c_{t} ct关系时只提到应用了tanh函数,这里其实还考虑了对 t a n h ( c t ) tanh(c_{t}) tanh(ct)施加了“门控”,调整了 t a n h ( c t ) tanh(c_{t}) tanh(ct)的各个元素的重要程度。由于这里的门管理了 h t h_{t} ht的输出,所以称为输出门(output gate)。公式如下:
o = σ ( x t W x ( o ) + h t − 1 W h ( o ) + b ( o ) ) o = \sigma(x_{t}W_{x}^{(o)}+h_{t-1}W_{h}^{(o)}+b^{(o)}) o=σ(xtWx(o)+ht−1Wh(o)+b(o))
o o o与 t a n h ( c t ) tanh(c_{t}) tanh(ct)的对应元素乘积,得到 h t h_{t} ht。
tanh的输出是 -1.0 ~ 1.0的实数,可以认为是表示某种被编码信息的强弱程度。sigmoid的输出是 0.0 ~ 1.0的实数,表示数据流出的比例。因此,多数情况下,门使用sigmoid函数作为激活函数,包含实质信息的数据使用tanh函数作为激活函数。
6.2.4 遗忘门
在记忆单元 c t − 1 c_{t-1} ct−1上添加一个忘记不必要信息的门,称为遗忘门(forget gate)。公式如下:
f = σ ( x t W x ( f ) + h t − 1 W h ( f ) + b ( f ) ) f = \sigma(x_{t}W_{x}^{(f)}+h_{t-1}W_h^{(f)}+b^{(f)}) f=σ(xtWx(f)+ht−1Wh(f)+b(f))
f f f与 c t − 1 c_{t-1} ct−1对应元素的乘积求得传递到当前时刻的记忆信息(删除了应该忘记的信息)。
6.2.5 新的记忆单元
除了删除上一时刻的记忆单元中应该忘记的信息,我们还需要向这个记忆单元添加应当记住的新信息,为此添加新的tanh节点,公式如下:
g = t a n h ( x t W x ( g ) + h t − 1 W h ( g ) + b ( g ) ) g=tanh(x_tWx^{(g)}+h_{t-1}W_h^{(g)}+b^{(g)}) g=tanh(xtWx(g)+ht−1Wh(g)+b(g))
g g g表示新的信息。
6.2.6 输入门
对上面的新的记忆单元 g g g添加门,控制信息流量(对新信息添加权重从而对信息进行取舍),称为输入门(input gate)。公式如下:
i = σ ( x t W x ( i ) + h t − 1 W h ( i ) + b ( i ) ) i = \sigma(x_tW_x^{(i)}+h_{t-1}W_h^{(i)}+b^{(i)}) i=σ(xtWx(i)+ht−1Wh(i)+b(i))
然后,将 i i i和 g g g的对应元素的乘积作为最终的新记忆添加到记忆单元中。
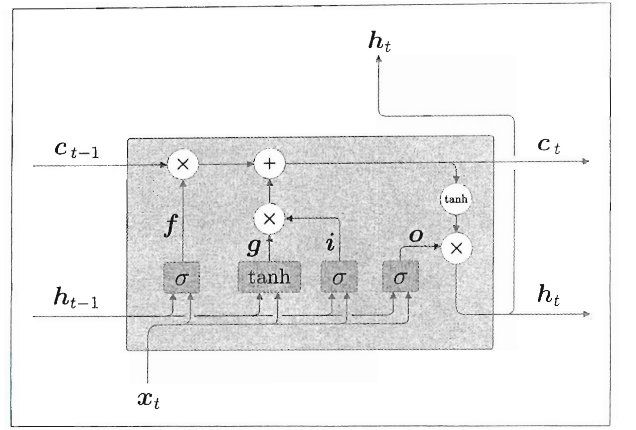
LSTM的整个内部处理如下图所示:
6.2.7 LSTM的梯度的流动
上面介绍完LSTM的结构,观察记忆单元 c c c的反向传播我们就会知道它为什么不会引起梯度消失。
记忆单元 c c c的反向传播仅流过"➕"和“✖️”节点。“➕”节点将上游传来的梯度原样流出,所以梯度没有变化。“✖️”节点进行的是对应元素的乘积计算(RNN是相同权重矩阵重复多次的矩阵乘积),而且每次乘积的门值不同,门值调节着梯度的大小,所以LSTM的记忆单元不会(难以)梯度消失。
6.3 使用LSTM的语言模型
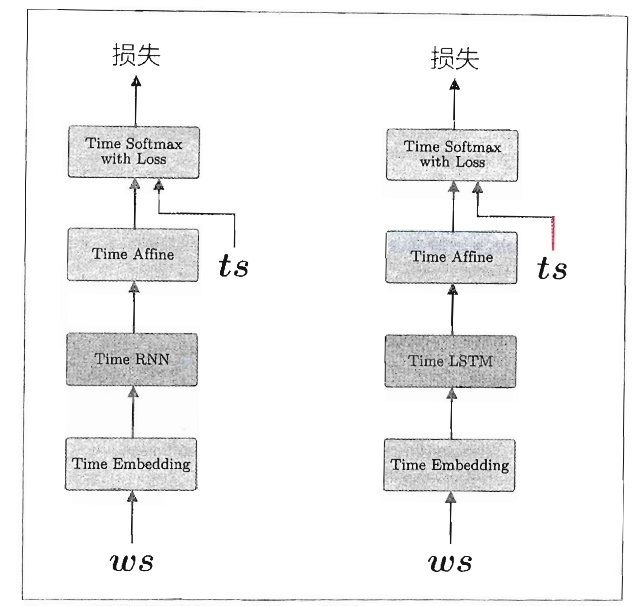
这里实现的语言模型和上一章几乎一样,唯一区别是这次用Time LSTM层替换了Time RNN层,如下图:
当前的使用LSTM层的语言模型有3点需要改进的地方,分别是:LSTM层的多层化、基于Dropout抑制过拟合和权重共享。
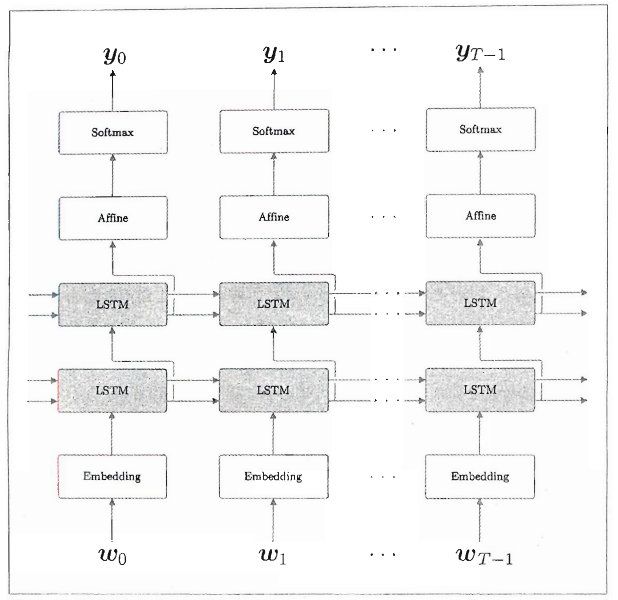
6.3.1 LSTM层的多层化
叠加多个LSTM层可以提高语言模型的精度,前一个LSTM层的隐藏状态是后面一个LSTM层的输入。具体要叠加几层,需要根据问题的复杂程度和数据规模来确定。
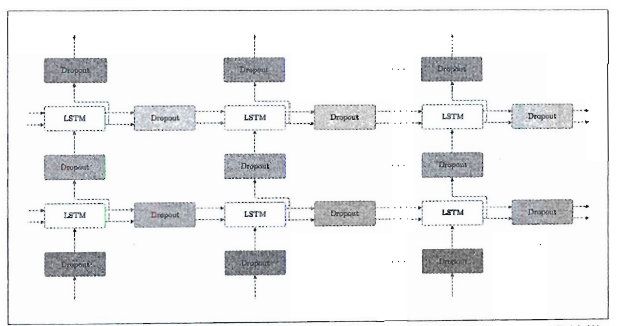
6.3.2 基于Dropout抑制过拟合
通过加深层,可以提高模型的表现力,但是这样往往会导致过拟合。抑制过拟合的常用方法有增加训练数据、降低模型的复杂度,以及对模型复杂度给予正则化的惩罚。Dropout也是一种正则化。考虑到噪声的积累,最好在垂直方向上插入Dropout层,这样无论沿时间方向(水平方向)前进多少,信息都不会丢失。常规的Dropout不适合用在时间方向上,但是"变分Dropout"可以,它的机制是同一层的Dropout使用相同的mask(决定是否传递数据的随机布尔值),因为mask被固定,信息的损失方式也被固定,所以可以避免常规Dropout发生的指数级信息损失。
6.3.3 权重共享
Embedding层和Affine层的权重共享,在不影响精度的提高的同时,可以大大减少学习的参数的数量,而且还能抑制过拟合。
6.4 总结
本章的主题是Gated RNN,我们先指出上一章的简单RNN中存在的梯度消失/爆炸问题,说明了作为替代层的Grated RNN(LSTM、GRU等)的有效性。介绍了使用LSTM层创建的语言模型,以及模型的优化。
下一章我们将介绍如何使用语言模型生成文本。