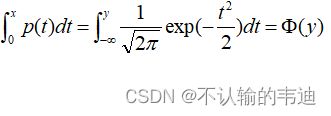生成模型笔记预备知识笔记——概率分布变换
最近准备课程分享，挑了一下最近比较火的AI作画方面的文章，结果发现这个领域水挺深的，也涉及到挺多数学方面的知识，得多做一下笔记。本文参考了这篇分享，算是这篇的一个读后笔记。PaperWeekly 第41期 | 互怼的艺术：从零直达 WGAN-GP
看了那些大佬发的文章，我发现高度真的会影响一个人看世界的角度。生成模型有许多伟大的想法，他们可以将这个世界的所有物体理解成高维空间的一个点，也可以把每一个事件看成是背后由一个隐藏的概率函数控制，并通过采样决定这个事件。而概率分布其实在生成模型中是很关键的一个想法。对于之前没有接触过生成模型的小伙伴来说，这里可能会有些稀里糊涂，但没关系，我们可以先来看一个比较小的问题。
如果有一个伪随机数程序能够生成 [0,1] 之间的均匀随机数，那么如何由它来生成服从正态分布的伪随机数？比如怎么将 U[0,1] 映射成 N(0,1)？
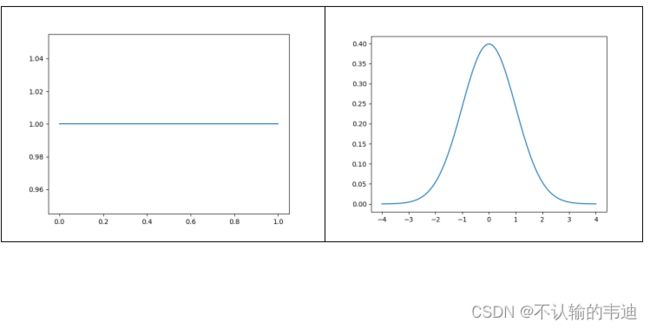
乍一看，这两个分布没有任何的相似处，从两个概率密度函数图像上来看也没有任何可取之处(注意定义域和值域)；但是我们可以把左边的线段给他往上面提，就像拉毛线一样，把均匀分布的图像拉成标准正态分布的样子，这个想法大家估计都有想实现的冲动，但是在数学上可不允许这样来。严格来说，我们需要找到一个具体的映射，使得X~U[0,1]经过一个函数Y=f(x)进行映射，Y~N(0,1)。
此时我们假设p(x)是这个X~U[0,1]的概率密度函数。在原始定义域上，在任意区间[x, x+dx]上的概率与其映射后在另一个域上[y, y+dy]的概率是相等的，即
.
由于dx,dy很小，所以可以近似认为在这个区间上的概率密度函数不变，而概率就等于概率密度函数乘上区间的长度。标准正态分布(高斯分布)的概率密度表达式为
于是就有下面的等式
熟悉概率论的小伙伴应该知道
是标准正态分布的概率分布函数(这里的积分上下限需要格外注意一下，左边是定义在[0,1]上的，而右边是实数域上的正态分布)。对这个式子中的y进行求解就能得到
其中
是
的反函数。
小伙伴应该知道，标准正态分布的概率密度函数表达式是无法使用初等函数进行表示的，它的反函数就更不可能显式地表达出来，因此我们到这里可以明白将均匀分布映射到高斯分布的函数y=f(x)是存在的，但是就是表达不出来。不过呢，我们可以通过一些骚操作来进行大致的函数拟合，因为我们拥有一个很好的工具——神经网络，它理论上可以拟合出任何一种函数。
具体的做法如下：给定一组服从某个分布的数据
(这里采用正态分布),要求我们找到一个映射函数f(x)，使得映射得到的
满足指定的分布z(这个分布是未知的，比如一张图片)。这里我们对问题进行梳理，首先我们不知道这个f(x)，但是可以使用神经网络拟合这个；其次我们不知道z是什么分布，这个问题的解决也是比较需要技巧的。
先解决第一个问题，如何使用神经网络训练出这个f(x)？很显然的，将给定的X丢到这个神经网络
中，然后它会产出一个与X同维度的Y，如果这个Y与指定的z是足够接近的，那么这个神经网络也就训练出来了。这里就涉及到一个问题，神经网络的训练是需要一个损失函数的，换句话说，我们需要告诉网络，你的产出与我们的预期接不接近，不接近的话就及时调整参数。在这个例子上就是得告诉网络，你产出的这个Y与这个z是不是服从同一个分布？
这就遇到了问题二了，我们不知道这个z是什么分布，甚至我们不知道这个产出来的Y是什么分布。但是问题不大哦，既然我们不知道这两个是什么分布，我们就老规矩，去估计、拟合、接近它。我们将实数域划分为若干个不相交的区间
然后使用一个简单的计数函数，用区间上的频率来估计区间的概率，即
其中N为指定样本的个数，函数
为指示函数，当
是为1，反之为0.
那这是什么意思呢？我这里画一个图相信大家就理解了。以标准正态分布为例，我们知道它大致长成下图这个样子
很可以的看出这是个漂亮的在实数域上连续的函数，如果我们将x轴进行一个划分，就像下图这样，那么落在各个区间的量的个数的样子也会和上图的趋势大致一致，这就是用频率近似替代概率的想法。
同理，我们也可以对神经网络输出的也进行这样的操作：
这样我们就得到了两个分布(神经网络输出Y的分布和指定z的分布)的概率估计，那又要怎么比较这两个是不是同一分布呢？这就需要使用一个工具叫KL散度(divergence)，它可以描述两个分布之间的差异，详细可以看一下这个人工智能学习笔记——KL散度_不认输的韦迪的博客-CSDN博客
但是这个度量是不对称的
于是我们改进一下使用JS距离
这样就对称了，从而我们的神经网络的损失函数就可以采用
结语
概率分布在很多典型的生成网络中都是主要思想，比如VAE、GAN等，当然我对这个了解也不是很深，文中可能也有些错误，希望大佬们斧正！不胜感激！