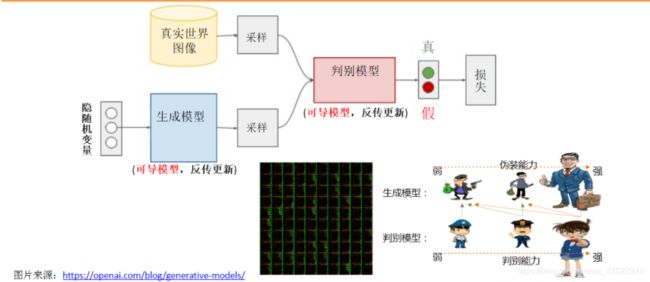
GAN&&StyleGAN学习笔记（1）

预备知识：GAN

1. GAN简介

GAN模型由生成器和判别器两部分构成。

生成模型就是一种寻找分布最优参数的过程，而这些参数更新不是来自于数据样本本身，而是来自于判别模型D的一个反传梯度，此处的分布参数只是一个黑盒子一样的映射函数：输入是一个随机变量，输出是我们想要的一个数据分布。

判别模型D的训练目的就是要尽量最大化自己的判别准确率。当这个数据被判别为来自于真实数据时，标注 1，自于生成数据时，标注 0。

GAN创新性地引入了一个判别模型（常用的有支持向量机和多层神经网络）。它的优化过程就是在寻找生成模型和判别模型之间的一个纳什均衡。

2. GAN原理分析

首先我们知道真实图片集的分布，x是一个真实图片，可以想象成一个向量，这个向量集合的分布就是

$P_{data}$ 。我们现在有的generator生成的分布可以假设为$P_G(x;\theta )$，这是一个由 $\theta$ 控制的分布，$\theta$ 是这个分布的参数。


假设我们在真实分布中取出一些数据$\{x^1,x^2,x^3.......,x^m\}$，我们想要计算一个似然$P_G(x^i;\theta )$。对于这些数据在生成模型中的似然就是$L={\sum }_{i=0}^n{P}_G(x^i;\theta )$。我们想要最大化这个似然，等价于让generator生成真实图片的概率最大，这就变成了一个最大似然估计问题，我们找一个$\theta {}^{\ast }$来表示这个最大化似然。


$\theta {}^{\ast }$ $=\arg$ $\underset{\theta }{\max }$ $\prod _{i=1}$ $P_G(x^i;\theta )$

$=\arg$ $\underset{\theta }{\max }$ $\log \prod _{i=1}$ $P_G(x^i;\theta )$

$=\arg$ $\underset{\theta }{\max }$ $\sum _{i=1}^m\log$ $P_G(x^i;\theta )$

$\approx$ $arg$ $\underset{\theta }{\max }$ $E_{x\sim P_{data}}$ $\log$ $P_G(x;\theta )$

$=\arg$ $\underset{\theta }{\max }$ ${\int }_x$ $P_{data}(x)$ $\log$ $P_G(x;\theta )dx$ $-$ ${\int }_x$ $P_{data}(x)$ $\log$ $P_{data}(x)dx$

$=\arg$ $\underset{\theta }{\max }$ ${\int }_x$ $P_{data}(x)$ $(\log$ $P_G(x;\theta )$ $-$ $\log$ $P_{data}(x))dx$

$=\arg$ $\underset{\theta }{\min }$ ${\int }_x$ $P_{data}(x)$ $\log$ $\frac{P_{data}(x)}{P_G(x;\theta )}$ $dx$

$=\arg$ $\underset{\theta }{\min }KL$ $(P_{data}(x)||P_G(x;\theta ))$

因为此时这m个数据，是从真实分布中取的，所以也就约等于真实分布中的所有x在 $P_G$ 分布中的log似然的期望。
真实分布中的所有x的期望，等价于求概率积分，所以可以转化成积分运算，因为减号后面的项和 $\theta$ 无关，所以添上之后还是等价的。然后提出共有的项，括号内的反转，max变min，就可以转化为 KL divergence 的形式了，KL divergence 描述的是两个概率分布之间的差异。

所以最大化似然，让generator最大概率生成图片，也就是要找一个 $\theta$ 让 $P_G$ 更接近于 $P_{data}$





图(a)中黑色大点虚线P(x)是真实的数据分布，绿线G(z)是通过生成模型产生的数据分布（输入是均匀分布变量z，输出是绿色的曲线）。蓝色的小点虚线D(x)代表判别函数。最终训练的目标就是使绿色曲线趋近于黑色曲线的分布，判别器对真实图像分布函数与生成图像分布函数各输出0.5的概率。

$\underset{G}{\min }$ $\underset{D}{\max }$ $V(D,G)=$ $E_{x\sim P_{data}(x)}$ $[\log D(x)]+E_{z\sim P_z(z)}[\log (1-D(G(z)))]$
这个式子的好处在于，固定G，$maxV(G,D)$ 就表示 $P_G$ 和 $P_{data}$ 之间的差异，然后找一个最好的G，让这个最大值最小，也就是两个函数分布之间的差异最小。


判别器采用随机梯度上升进行更新 ${▽}_{{\theta }_d}$ $\frac{1}{m}$ $\sum _1^m$ $[\log D(x^{(i)})+\log (1-D(G(z^{(i)})))]$
${\theta }_d\leftarrow {\theta }_d+\eta ▽V({\theta }_d)$

生成器采用随机梯度下降进行更新 ${▽}_{{\theta }_g}$ $\frac{1}{m}$ $\sum _1^m\log (1-D(G(z^{(i)})))$
${\theta }_g\leftarrow {\theta }_g-\eta ▽V({\theta }_g)$


其实两类更新都是对于$G(z)$的影响，判别器希望$D(G(z^{(i)}))$越小，生成器希望$D(G(z^{(i)}))$越大。

GAN论文链接

预备知识：ProGAN

Pro GAN（渐进式增长GAN）提出的想法是，我们只需要一个 GANs 就能产生 1024×1024 图片。但是一开始的时候网络非常浅，只能学习低分辨率（4×4）的图片生成，随着训练进行，我们逐渐向生成器和判别器网络中添加层，进而去学习更高分辨率的图片生成，最终不断的更新，从而能学习到 1024×1024 分辨率的图片生成。

ProGAN图片生成过程动态图

ProGAN论文链接

正文开始：StyleGAN

StyleGAN论文链接

StyleGAN论文中文翻译版链接

StyleGAN简介

Style GAN 是在Pro GAN的基础上产生的模型，沿用了其渐进式生成网络，在生成器的基础上进行了修改：移除了传统的输入，加入了噪声生成随机细节；增添了一些附加模块：映射网络、样式模块（AdaIN）。

1：移除传统输入，加入映射网络是此论文的一大亮点，目的是为了解纠缠（解耦合），使特征更好地分离，从而更加随意生成图像。后面解释。

2：加入噪声，是为了使生成图像更加真实。人类肖像中有许多方面可以被视为随机的，例如毛发、雀斑或皮肤毛孔的确切位置。只要它们遵循正确的分布，任何这些都可以在不影响我们对图像的感知的情况下进行随机化。

3：加入样式模块，在每一层进行风格添加，从低分辨率到高分辨率由Style控制。

Style GAN与Pro GAN模型一致，不同分辨率下，影响不同的特征

在粗糙分辨率（$4^2$—$8^2$）影响姿势、一般发型、面部形状等；
在中间层（$16^2$—$32^2$）影响更精细的面部特征、发型、眼睛的睁开或是闭合等；
在精细分辨率($64^2$—$1024^2$)影响颜色（眼睛、头发和皮肤）和微观特征；

StyleGAN详细分析

我将按照StyleGAN的网络模型顺序分析该模型的架构，虚线左边是ProGAN的生成网络，虚线右边是StyleGAN的映射网络和生成网络，只介绍StyleGAN的映射网络和生成网络。

1、首先分析一下$Latent$ $z\in Z$

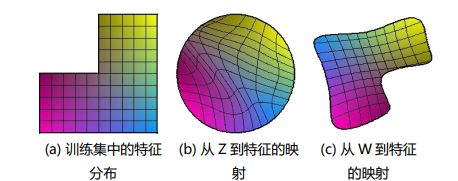
每一张图像都由各种特征组合而成，最原始的图像的某些特征可能无法简单地用一个维度或者多个维度的数据表示出来，耦合性较高，那么通过映射的方式将图像映射到其他空间中，使本来不容易表示的特征可以通过一维或者多维的数据进行表示，从而方便模型学习。

$latent$ $code$ 简单理解就是，为了更好的对数据进行分类或生成，需要对数据的特征进行表示，但是数据有很多特征，这些特征之间相互关联，耦合性较高，导致模型很难弄清楚它们之间的关联，使得学习效率低下，因此需要寻找到这些表面特征之下隐藏的深层次的关系，将这些关系进行解耦，得到的隐藏特征，即$latent$ $code$，由 $latent$ $code$组成的空间就是 $latent$ $space$。

总之，$latent$ $code$ $Z$是由初始图像解耦之后得到的易于模型学习的图像的表示形式，由一维或者多维的数据表示图像特征（包括隐藏特征）

不仅仅$latent$ $code$是为了解耦，将特征进行分离，特征由一个维度或者多个维度表示。之后的$Mapping$ $Network$是为了进一步解耦，达到使所有的特征都只需要一个维度控制。


2、其次经过归一化（$Normalize$）

每个像素矩阵的取值均是0 - 255之间的整数，虽然可以直接将原始图像的像素真实值直接作为神经网络模型的训练数据，但是这可能会给我们模型的训练过程带来一些问题，因为在深度神经网络训练时一般使用较小的权重值来进行拟合，而当训练数据的值是较大整数值时，可能会减慢模型训练的过程。

如果我们在将图像输入到神经网络之前对图像做像素值归一化的处理，即将像素值缩放到0 - 1之间，就能够避免很多不必要的麻烦。（当图像的像素处于0 - 1范围时，由于仍然介于0 - 255之间，所以图像依旧是有效的，并且可以正常查看图像。）

3、$MappingNetwork$

然后再经过$MappingNetwork$ ，也就是8个全连接层。$MappingNetwork$的作用就是解纠缠，将$latent$ $code$ $Z$进一步解耦成为$latent$ $code$ $W$，达到使每个维度的数据控制一个特征。

如果不加这个$MappingNetwork$的话，后续得到的18个控制向量之间会存在特征纠缠的现象——比如说我们想调节8x8分辨率上的控制向量（假设它能控制人脸生成的角度），但是我们会发现32x32分辨率上的控制内容（譬如肤色）也被改变了，这个就叫做特征纠缠。

为何$MappingNetwork$能够学习到特征解缠呢？简单来说，如果仅使用输入向量来控制视觉特征，能力是非常有限的，因此它必须遵循训练数据的概率密度。例如，如果黑头发的人的图像在数据集中更常见，那么更多的输入值将会被映射到该特征上。因此，该模型无法将部分输入（向量中的元素）映射到特征上，这就会造成特征纠缠。然而，通过使用另一个神经网络，该模型可以生成一个不必遵循训练数据分布的向量，并且可以减少特征之间的相关性。

经过$MappingNetwork$输出的$w$，此处为$w^{{}^{\prime }}$或许更为合适，文章中提到，运用了截断技巧，$w^{{}^{\prime }}=\bar{w}+\psi (w-\bar{w})$使一些低概率密度的点聚拢到一起，但是又不会改变点与点之间的距离关系。（从数据分布来说，低概率密度的数据在网络中的表达能力很弱，直观理解就是，低概率密度的数据出现次数少，能影响网络梯度的机会也少，但并不代表低概率密度的数据不重要。）

4、$Synthesis$ $Nertwork$

首先看到的是$const$ 4x4x512，此处由随机噪声改为了$const$ 4x4x512，原因是在粗糙分辨率层，使用常量与使用随机噪声几乎没有大的差别。在接下来是对每个分辨率层进行相应的风格迁移操作以及噪声添加操作。共9层（4x4 —— 1024x1024）每一层都要经历上采样（4 x 4分辨率层无上采样过程，因为本身给的就是4 x 4 的const）、AdaIN过程、Conv 3x3卷积过程、AdaIN过程。

接下来会分别介绍 AdaIN过程，Conv 3x3过程、upsample（上采样过程）：

（1）AdaIN过程

首先，看A模块，A是仿射变换的过程，将$w$（也可写 $w^{{}^{\prime }}$）通过仿射变换，变为Style。
$w$（也可写 $w^{{}^{\prime }}$）通过广播操作得到18个完全相同的$w$（或 $w^{{}^{\prime }}$）（代码中的体现其实就是简单的复制），真正的灵魂在于仿射变换A的参数学习，18个A分别学习到不同分辨率下控制当前style的参数，实现了对style的分离，即不同分辨率下的style生成控制。（仿射变换A就是一个全连接层，这样就能通过网络迭代，学习到自己层相关的权重参数）。

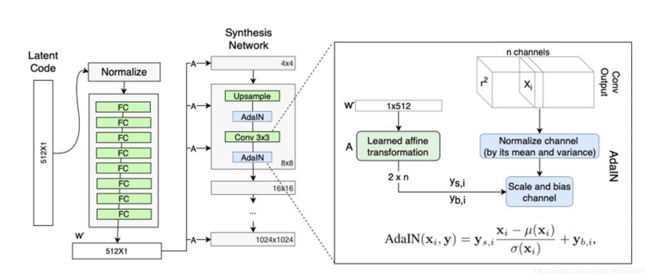
AdaIN中没有可学习的仿射参数，即仿射参数不是通过学习得到。AdaIN接收两个信息源：内容输入x 和风格输入y ，每个特征图xi独立进行标准化，然后对每个特征图分别使用style中学习到的的平移和缩放因子进行尺度和平移变换，将x的通道级均值和标准差匹配到y的通道级均值和标准差上。

简单地来讲，AdaIN在feature map层面上通过改变特征的数据分布来实现风格迁移，计算开销和存储开销都较小，且易实现。

那么在上图中$w^{{}^{\prime }}$ （1x512规模）怎么转化成了 2 x n 规模的呢？（由代码可得，n channels的 n 在前四个分辨率层是512，之后每层分别是256，128，64，32，16）单纯的将n当作512来看的话，等价于1x512——>2x512，前者的1指的是当前维度的特征值，可以看作将一张图片通过全连接的方式压缩成了一个值；后者的2指的是当前特征图的均值和方差。我的理解是会不会是一个反卷积的过程，将一个代表当前维度的值还原成了一张当前分辨率的图片，对图片中各个像素点的值求均值和方差，就相当于得到了当前这个维度的style（$y_{s,i}$ 和 $y_{b,i}$）【此处的理解还在推敲，不一定正确，希望读者加入自己的思考来理解。】

其次，看B模块，采用类似于AdaIN机制的方式添加噪声，即在AdaIN模块之前向每个通道添加一个缩放过的噪声，并稍微改变其操作的分辨率级别特征的视觉表达方式。加入噪声后的生成人脸往往更加逼真与多样。

(a) 噪音适用于所有层。(b) 没有噪音。 （c）仅有精细层的噪音。(d) 仅粗糙层的噪音。

我们可以看到，人为地忽略噪音会导致无意义的“绘画”外观。 粗糙的噪音会导致头发大规模卷曲和出现更大的背景特征，而细微的噪音则会带来更精细的头发卷曲，更细致的背景细节和皮肤毛孔。

StyleGAN中的风格混合

简单原理就是：

在生成图像时用一个隐码（source）产生的样式覆盖另一个隐码（destination）产生的样式的子集，此图是将source B的隐码在不同的分辨率分别作用于Source A。

在粗糙分辨率（$4^2$—$8^2$）用source B的样式覆盖source A的样式，产生的图像的高级特征（姿势、头发样式、脸的形状和眼镜）从source B图像中复制，而source A的颜色（眼睛、头发、光线）和更精细的面部特征被保留下来。说明该尺度的样式控制了生成图像的高级特征。

在中间层（$16^2$—$32^2$）用source B的样式覆盖source A的样式，合成的图像将会从source B中继承较小尺度的面部特征（头发的样式、眼睛的闭合），而source A的姿势、脸的形状、眼镜等被保留。说明该尺度的样式控制了生成图像的较小尺度的面部特征。

在精细分辨率($64^2$—$1024^2$)用source B的样式覆盖source A的样式，主要复制了source B中的颜色。说明该尺度的样式控制了生成图像的更低尺度的特征-颜色。

两种新的量化耦合度的方法

感知路径长度（Perceptual path length）与 线性可分性（linear separability）

感知路径长度 —— 参考这个链接的Perceptual path length部分
球面插值与线性插值的理解——参考这个链接的插值部分
线性可分性 —— 参考这个链接的linear separability部分
条件熵的理解 —— 参考这个链接的条件熵部分

参考文章

https://blog.csdn.net/WhaleAndAnt/article/details/105074223
https://blog.csdn.net/u013972559/article/details/85230111
https://zhuanlan.zhihu.com/p/27295635
https://zhuanlan.zhihu.com/p/263554045
https://zhuanlan.zhihu.com/p/63230738

https://blog.csdn.net/briblue/article/details/83063170?utm_medium=distribute.pc_relevant.none-task-blog-baidujs_baidulandingword-0&spm=1001.2101.3001.4242

https://blog.csdn.net/weixin_44695969/article/details/102923699?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-3.control&dist_request_id=&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-3.control