神经网络中的激活函数

  在多层神经网络中，上层节点的输出和下层节点的输入之间具有一个函数关系，这个函数称为激活函数，又称激励函数。
  引入非线性函数作为激励函数，这样深层神经网络表达能力就更加强大（不再是输入的线性组合，而是几乎可以逼近任意函数）。那有哪些激活函数呢？他们各自的优劣是什么呢？下面我们来具体介绍一下：

1 Sigmoid 函数

  Sigmoid 是常用的非线性的激活函数，数学公式为：
$$f(x)=\frac{1}{1+e^{-z}}$$

  由图可知，左端趋近于 0，右端趋近于 1，且两端都趋于饱和。能够把输入的连续实值变换为 0~1 之间的输出；如果是非常大的负数，那么输出就是 0；如果是非常大的正数，输出就是 1。

  缺点：
  （1）Sigmoid 函数饱和时梯度值非常小，在深度神经网络中梯度反向传递时容易导致梯度消失。
  （2）Sigmoid 的 output 不是 0 均值，这会导致后一层的神经元将得到上一层输出的非 0 均值的信号作为输入。
  （3）其解析式中含有幂运算，计算机求解时相对来讲比较耗时，较大地增加训练时间。

2 Tanh 函数

  Tanh 函数数学公式为：
$$f(x)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$$
  解决了 Sigmoid 函数的不是 0 均值输出问题，然而梯度消失和幂运算的问题仍然存在。

3 ReLU 函数

  ReLU 函数数学公式为：
$$relu(x)=max(x,0)$$
  ReLu 是一个分段函数，显然其导数在正半轴为 1，负半轴为 0，这样它在整个实数域上有一半的空间是不饱和的。ReLu 很简单，但近几年被广泛使用。

  优点：解决了梯度消失问题，计算速度非常快，收敛速度远快于 sigmoid 和 tanh。

  缺点：当反向传播过程中有一个非常大的梯度经过时，反向传播更新后可能导致权重分布中心小于 0，导致该处的导数始终为 0，因此反向传播无法更新权重，即进入失活状态。

4 Leaky ReLU 函数

  Leaky ReLU 函数数学公式为：
$$leaky\_relu(x)=\{\begin{array}{ll}x,& \text{if x≥0}\\ \alpha x,& \text{if x<0}\end{array},\alpha 通常取0.01$$

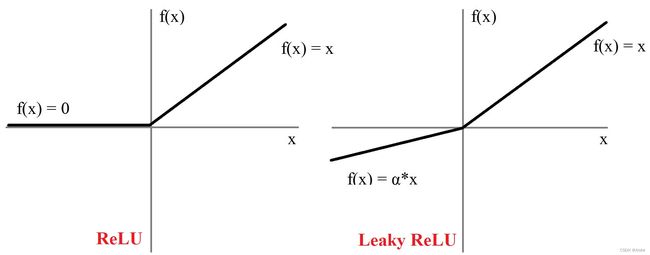
  ReLU 是将所有的 x 负半轴的值都设为0，而 Leaky ReLU 是给 x 负半轴赋予一个非零斜率。

  特点：Leaky ReLU 函数的范围是负无穷到正无穷，有助于扩大 ReLU 函数的范围； x 负半轴的值不再为 0，可调整负值的零梯度问题。

5 GELU 函数

  GELU (Gaussian Error Linear Unit) 高斯误差线性单元，在 NLP 领域中被广泛应用。
  GELU 函数数学公式为：
$$GELU(x)=0.5x(1+tanh(\sqrt{\frac{2}{\pi }}(x+0.044715x^3)))$$

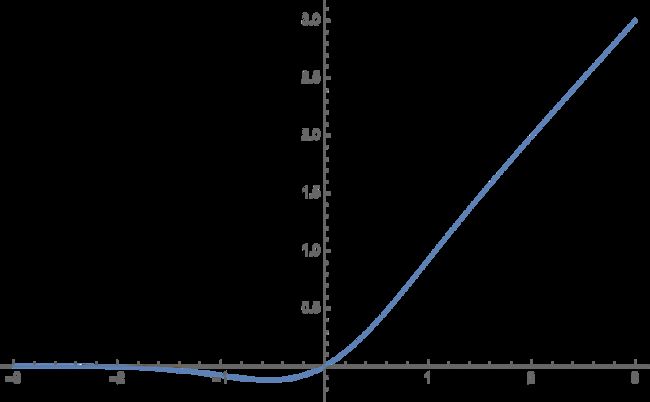
  GELU 函数其实就是某些函数（比如双曲正切函数 tanh）与近似数值的组合，x 越大就越有可能被保留，x 越小就越有可能被归置为 0。

  特点：GELU 激活函数与随机正则化有关，可以起到自适应 Dropout 的效果；适用于 NLP 领域；能避免梯度消失问题。

6 Swish 函数

  Swish 的设计受到了 LSTM 和 sigmoid 函数使用的启发。
  Swish 函数数学公式为：
$$Swish(x)=x\ast sigmoid(\beta x)$$

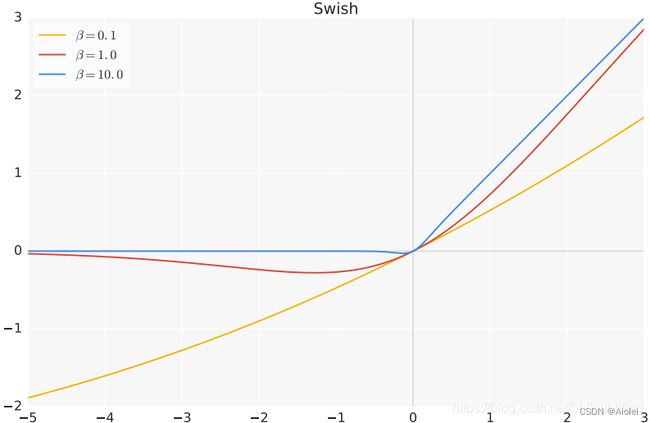
   β 取不同的值，函数图像会随之改变。
  当 β = 0 时，$sigmoid(\beta x)=0.5$，Swish 激活函数变为线性函数 $Swish(x)=\frac{x}{2}$
  当 β = $\infty$ 时，$sigmoid(\beta x)=1或0$，Swish 激活函数变为 0 或 x，相当于ReLU；
  因此，Swish 函数可以看作是介于线性函数与 ReLU 函数之间的平滑函数。

  特点：具有平滑特性，有助于防止慢速训练期间，梯度逐渐接近 0 并导致饱和。