利用pytorch完成BP神经网络的搭建
使用pytorch完成神经网络的搭建
一.搭建一个最简单的BP神经网络
BP神经网络前向传播:
h = w 1 x y = w 2 h h=w1x\\ y=w2h h=w1xy=w2h
import torch
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from tqdm import tqdm
import time
# 超参数定义(由于我们的隐藏层只有一层,所以可以直接定义为超参数)
batch_size=100
input_feature=100
hidden_feature=1000
output_feature=10
learning_rate=1e-6
epochs=1000
# 参数初始化
x=torch.randn(batch_size,input_feature)
y=torch.randn(batch_size,output_feature)
w1=torch.randn(input_feature,hidden_feature)
w2=torch.randn(hidden_feature,output_feature)
Epoch=[]
Loss=[]
# 迭代训练
for epoch in tqdm(range(1,epochs+1)):
# 前向传播
h=x.mm(w1) # (bs,hf)
y_pred=h.mm(w2) # (bs,of)
loss=(y_pred-y).pow(2).sum()
Epoch.append(epoch)
Loss.append(loss)
if epoch%50==0:
print("Epoch:{},loss:{}".format(epoch,loss))
# 后向传播
grad_y_pred=2*(y_pred-y) # (bs,of)
grad_w2=grad_y_pred.t().mm(h) # (of,hf)
grad_h=grad_y_pred.mm(w2.t()) # (bs,of)
grad_w1=grad_h.t().mm(x) # (hf,if)
# 参数微调
w1-=learning_rate*grad_w1.t()
w2-=learning_rate*grad_w2.t()
time.sleep(0.01)
Epoch=np.array(Epoch)
Loss=np.array(Loss)
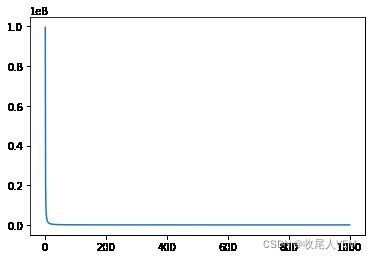
plt.plot(Epoch,Loss)
plt.show()
6%|▌ | 55/1000 [00:00<00:14, 63.82it/s]
Epoch:50,loss:123946.703125
11%|█ | 111/1000 [00:01<00:13, 64.45it/s]
Epoch:100,loss:45572.93359375
16%|█▌ | 160/1000 [00:02<00:13, 64.50it/s]
Epoch:150,loss:25665.857421875
21%|██ | 209/1000 [00:03<00:12, 64.00it/s]
Epoch:200,loss:17030.986328125
26%|██▌ | 258/1000 [00:04<00:11, 63.59it/s]
Epoch:250,loss:12279.029296875
31%|███ | 307/1000 [00:04<00:10, 63.77it/s]
Epoch:300,loss:9323.0244140625
36%|███▌ | 356/1000 [00:05<00:10, 63.67it/s]
Epoch:350,loss:7347.61865234375
40%|████ | 405/1000 [00:06<00:09, 64.10it/s]
Epoch:400,loss:5961.97021484375
46%|████▌ | 461/1000 [00:07<00:08, 64.44it/s]
Epoch:450,loss:4953.791015625
51%|█████ | 510/1000 [00:07<00:07, 63.19it/s]
Epoch:500,loss:4197.994140625
56%|█████▌ | 559/1000 [00:08<00:06, 63.91it/s]
Epoch:550,loss:3616.96044921875
61%|██████ | 608/1000 [00:09<00:06, 64.82it/s]
Epoch:600,loss:3160.400390625
66%|██████▌ | 657/1000 [00:10<00:05, 63.21it/s]
Epoch:650,loss:2794.73681640625
71%|███████ | 706/1000 [00:11<00:04, 62.82it/s]
Epoch:700,loss:2496.922607421875
76%|███████▌ | 755/1000 [00:11<00:03, 64.82it/s]
Epoch:750,loss:2250.6728515625
80%|████████ | 804/1000 [00:12<00:03, 63.79it/s]
Epoch:800,loss:2044.34912109375
86%|████████▌ | 860/1000 [00:13<00:02, 63.53it/s]
Epoch:850,loss:1869.3782958984375
91%|█████████ | 909/1000 [00:14<00:01, 64.22it/s]
Epoch:900,loss:1719.3748779296875
96%|█████████▌| 958/1000 [00:14<00:00, 63.20it/s]
Epoch:950,loss:1589.4639892578125
100%|██████████| 1000/1000 [00:15<00:00, 63.88it/s]
Epoch:1000,loss:1475.9722900390625
二.使用pytorch自动求导功能搭建神经网络
import torch
import matplotlib.pyplot as plt
import numpy as np
import tqdm
from torch.autograd import Variable
# 超参数定义(由于我们的隐藏层只有一层,所以可以直接定义为超参数)
batch_size=100
input_feature=100
hidden_feature=1000
output_feature=10
learning_rate=1e-6
epochs=1000
# 参数初始化
x=Variable(torch.randn(batch_size,input_feature),requires_grad=False)
y=Variable(torch.randn(batch_size,output_feature),requires_grad=False)
w1=Variable(torch.randn(input_feature,hidden_feature),requires_grad=True)
w2=Variable(torch.randn(hidden_feature,output_feature),requires_grad=True)
Epoch=[]
Loss=[]
# 迭代训练
for epoch in tqdm.tqdm(range(1,epochs+1)):
# 前向传播
h=x.mm(w1) # (bs,hf)
y_pred=h.mm(w2) # (bs,of)
loss=(y_pred-y).pow(2).sum()
Epoch.append(epoch)
Loss.append(loss.data)
if epoch%50==0:
print("Epoch:{},loss:{}".format(epoch,loss))
# 后向传播
loss.backward()
# 参数微调
w1.data-=learning_rate*w1.grad.data
w2.data-=learning_rate*w2.grad.data
# pytorch自动求导功能梯度会累积
w1.grad.data.zero_()
w2.grad.data.zero_()
Epoch=np.array(Epoch)
Loss=np.array(Loss)
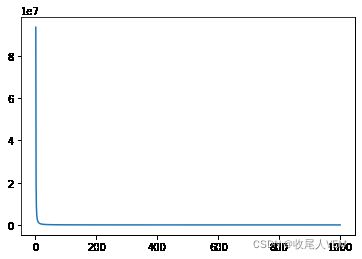
plt.plot(Epoch,Loss)
plt.show()
27%|██▋ | 268/1000 [00:00<00:00, 1307.45it/s]
Epoch:50,loss:113461.265625
Epoch:100,loss:43724.5625
Epoch:150,loss:24828.20703125
Epoch:200,loss:16095.78515625
Epoch:250,loss:11224.177734375
Epoch:300,loss:8250.69140625
52%|█████▏ | 522/1000 [00:00<00:00, 1146.03it/s]
Epoch:350,loss:6329.505859375
Epoch:400,loss:5032.93994140625
Epoch:450,loss:4124.7939453125
Epoch:500,loss:3467.188720703125
Epoch:550,loss:2976.24560546875
75%|███████▌ | 753/1000 [00:00<00:00, 1125.28it/s]
Epoch:600,loss:2599.2880859375
Epoch:650,loss:2302.247802734375
Epoch:700,loss:2062.63134765625
Epoch:750,loss:1865.1539306640625
Epoch:800,loss:1699.3299560546875
100%|██████████| 1000/1000 [00:00<00:00, 1115.32it/s]
Epoch:850,loss:1557.7520751953125
Epoch:900,loss:1435.1156005859375
Epoch:950,loss:1327.5877685546875
Epoch:1000,loss:1232.2830810546875
三.自定义前向传播函数
import torch
import matplotlib.pyplot as plt
import numpy as np
import tqdm
from torch.autograd import Variable
# 超参数定义(由于我们的隐藏层只有一层,所以可以直接定义为超参数)
batch_size=100
input_feature=100
hidden_feature=1000
output_feature=10
learning_rate=1e-6
epochs=1000
# 参数初始化
x=Variable(torch.randn(batch_size,input_feature),requires_grad=False)
y=Variable(torch.randn(batch_size,output_feature),requires_grad=False)
w1=Variable(torch.randn(input_feature,hidden_feature),requires_grad=True)
w2=Variable(torch.randn(hidden_feature,output_feature),requires_grad=True)
class Net(torch.nn.Module):
def __init__(self) -> None:
super(Net,self).__init__()
def forward(self,input,w1,w2):
x = torch.mm(input,w1)
x = torch.mm(x,w2)
return x
Epoch=[]
Loss=[]
model=Net()
# 迭代训练
for epoch in tqdm.tqdm(range(1,epochs+1)):
# 前向传播
y_pred=model(x,w1,w2)
loss=(y_pred-y).pow(2).sum()
Epoch.append(epoch)
Loss.append(loss.data)
if epoch%50==0:
print("Epoch:{},loss:{}".format(epoch,loss))
# 后向传播
loss.backward()
# 参数微调
w1.data-=learning_rate*w1.grad.data
w2.data-=learning_rate*w2.grad.data
# pytorch自动求导功能梯度会累积
w1.grad.data.zero_()
w2.grad.data.zero_()
Epoch=np.array(Epoch)
Loss=np.array(Loss)
plt.plot(Epoch,Loss)
plt.show()
27%|██▋ | 268/1000 [00:00<00:00, 1330.29it/s]
Epoch:50,loss:108250.15625
Epoch:100,loss:42146.89453125
Epoch:150,loss:23690.796875
Epoch:200,loss:15645.31640625
Epoch:250,loss:11309.4345703125
Epoch:300,loss:8637.078125
53%|█████▎ | 529/1000 [00:00<00:00, 1224.36it/s]
Epoch:350,loss:6837.70361328125
Epoch:400,loss:5552.3505859375
Epoch:450,loss:4596.23779296875
Epoch:500,loss:3864.13232421875
Epoch:550,loss:3291.485595703125
78%|███████▊ | 776/1000 [00:00<00:00, 1189.72it/s]
Epoch:600,loss:2836.02734375
Epoch:650,loss:2468.908447265625
Epoch:700,loss:2169.5869140625
Epoch:750,loss:1923.091552734375
Epoch:800,loss:1718.2396240234375
100%|██████████| 1000/1000 [00:00<00:00, 1151.18it/s]
Epoch:850,loss:1546.5772705078125
Epoch:900,loss:1401.564697265625
Epoch:950,loss:1278.1241455078125
Epoch:1000,loss:1172.29345703125
四.使用torch.nn包库大幅度简化搭建过程
import torch
import matplotlib.pyplot as plt
import numpy as np
import tqdm
from torch.autograd import Variable
from torch.nn import *
from torch.optim import Adam
# 超参数定义(由于我们的隐藏层只有一层,所以可以直接定义为超参数)
batch_size=100
input_feature=100
hidden_feature=1000
output_feature=10
learning_rate=1e-6
epochs=1000
loss_f=MSELoss()
# 参数初始化
x=Variable(torch.randn(batch_size,input_feature),requires_grad=False)
y=Variable(torch.randn(batch_size,output_feature),requires_grad=False)
w1=Variable(torch.randn(input_feature,hidden_feature),requires_grad=True)
w2=Variable(torch.randn(hidden_feature,output_feature),requires_grad=True)
Epoch=[]
Loss=[]
model=Sequential(
Linear(input_feature,hidden_feature),
Linear(hidden_feature,output_feature)
)
# optimizer需要传入训练参数和lr
optim=Adam(model.parameters(),lr=learning_rate)
print(model)
# 迭代训练
for epoch in tqdm.tqdm(range(1,epochs+1)):
# 前向传播
y_pred=model(x)
loss=loss_f(y_pred,y)
Epoch.append(epoch)
Loss.append(loss.data)
if epoch%50==0:
print("Epoch:{},loss:{}".format(epoch,loss))
optim.zero_grad()
# 后向传播
loss.backward()
# 参数微调
optim.step()
# for parm in model.parameters():
# parm.data-=parm.grad.data*learning_rate
Epoch=np.array(Epoch)
Loss=np.array(Loss)
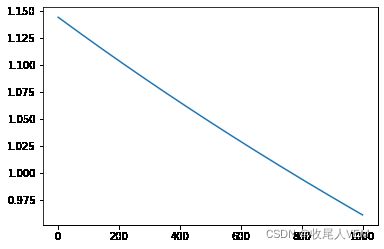
plt.plot(Epoch,Loss)
plt.show()
Sequential(
(0): Linear(in_features=100, out_features=1000, bias=True)
(1): Linear(in_features=1000, out_features=10, bias=True)
)
12%|█▏ | 123/1000 [00:00<00:01, 619.40it/s]
Epoch:50,loss:1.133939266204834
Epoch:100,loss:1.1237508058547974
Epoch:150,loss:1.1136993169784546
25%|██▍ | 247/1000 [00:00<00:01, 599.47it/s]
Epoch:200,loss:1.1037803888320923
Epoch:250,loss:1.0939908027648926
36%|███▋ | 364/1000 [00:00<00:01, 514.30it/s]
Epoch:300,loss:1.084326982498169
Epoch:350,loss:1.0747860670089722
47%|████▋ | 471/1000 [00:00<00:01, 497.48it/s]
Epoch:400,loss:1.065364956855774
Epoch:450,loss:1.056060791015625
57%|█████▋ | 574/1000 [00:01<00:00, 460.62it/s]
Epoch:500,loss:1.0468708276748657
Epoch:550,loss:1.037792682647705
Epoch:600,loss:1.028823733329773
74%|███████▎ | 737/1000 [00:01<00:00, 509.46it/s]
Epoch:650,loss:1.0199618339538574
Epoch:700,loss:1.0112043619155884
Epoch:750,loss:1.002549648284912
90%|████████▉ | 899/1000 [00:01<00:00, 520.97it/s]
Epoch:800,loss:0.9939954280853271
Epoch:850,loss:0.9855398535728455
95%|█████████▌| 952/1000 [00:01<00:00, 506.24it/s]
Epoch:900,loss:0.9771808981895447
Epoch:950,loss:0.968916654586792
100%|██████████| 1000/1000 [00:01<00:00, 511.05it/s]
Epoch:1000,loss:0.9607456922531128
五.手写数字识别
import torch
from torchvision import datasets,transforms # 用于图像的处理、导入和预览
from torch.autograd import Variable
import torchvision
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
from torch.nn import *
import tqdm
data_transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(mean=[0.5],std=[0.5])
])
# mean可以自行定义,但是标准差变换所需的mean和std一般是来自与原数据
data_train=datasets.MNIST(
root="../data/",
transform=data_transform,
train=True)
data_test=datasets.MNIST(
root='../data/',
transform=data_transform,
train=False)
data_loader_train=DataLoader(
dataset=data_train,
batch_size=64,
shuffle=True)
data_loader_test=DataLoader(
dataset=data_test,
batch_size=64,
shuffle=True)
images,labels=next(iter(data_loader_train)) # 得到第一个batch的数据信息
imgs=torchvision.utils.make_grid(images)
# print(images,images.shape)
# print(labels,labels.shape)
# img=images[0]
# img=torch.reshape(img,(28,28,1))
# plt.imshow(img)
# print("images[0]'s label:{}".format(labels[0]))
标准差变换:
$$
x_{normalization}=\frac{x-mean}{std}
$$
from torch.nn import CrossEntropyLoss
from torch.optim import Adam
class Model(torch.nn.Module):
def __init__(self) -> None:
super(Model,self).__init__()
self.conv1=Sequential(
Conv2d(1,64,kernel_size=3,stride=1,padding=1),
ReLU(),
Conv2d(64,128,kernel_size=3,stride=1,padding=1),
ReLU(),
MaxPool2d(stride=2,kernel_size=2)
)
self.dense=Sequential(
Linear(14*14*128,1024),
ReLU(),
Dropout(p=0.5),
Linear(1024,10)
)
def forward(self,x):
x=self.conv1(x)
x=x.view(-1,14*14*128)
x=self.dense(x)
return x
device=torch.device("cuda" if torch.cuda.is_available() else "cpu")
model=Model()
epochs=5
lr=1e-5
weight_save_path="../weight/"
loss_fn=CrossEntropyLoss()
optimizer=Adam(model.parameters(),lr=lr)
print(model)
model=model.to(device)
state={'net':model.state_dict(), 'optimizer':optimizer.state_dict(), 'epoch':epochs}
for epoch in range(epochs):
running_loss=0.0
running_correct=0
print("Epoch:{}/{}".format(epoch+1,epochs))
print('-'*10)
for data in tqdm.tqdm(data_loader_train):
X_train,y_train=data
X_train,y_train=Variable(X_train).to(device),Variable(y_train).to(device)
outputs=model(X_train)
_,pred=torch.max(outputs.data,1)
optimizer.zero_grad()
loss=loss_fn(outputs,y_train)
loss.backward()
optimizer.step()
running_loss+=loss.data
running_correct+=torch.sum(pred==y_train.data)
testing_correct=0
for data in data_loader_test:
X_test,y_test=data
X_test,y_test=Variable(X_test).to(device),Variable(y_test).to(device)
outputs=model(X_test)
_,pred=torch.max(outputs.data,1)
testing_correct+=torch.sum(pred==y_test.data)
print("Loss is {},Train Accuracy is {},Test Accuracy is {}".format
(running_loss/len(data_train),running_correct/len(data_train),testing_correct/len(data_test)))
torch.save(state,'../weight/2022_1_26_mnist_17_17.pth')
Model(
(conv1): Sequential(
(0): Conv2d(1, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU()
(2): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(3): ReLU()
(4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(dense): Sequential(
(0): Linear(in_features=25088, out_features=1024, bias=True)
(1): ReLU()
(2): Dropout(p=0.5, inplace=False)
(3): Linear(in_features=1024, out_features=10, bias=True)
)
)
Epoch:0/5
----------
100%|██████████| 938/938 [00:22<00:00, 41.08it/s]
Loss is 0.010012555867433548,Train Accuracy is 0.8397499918937683,Test Accuracy is 0.9235000014305115
Epoch:1/5
----------
100%|██████████| 938/938 [00:20<00:00, 45.16it/s]
Loss is 0.003718222491443157,Train Accuracy is 0.9320999979972839,Test Accuracy is 0.9441999793052673
Epoch:2/5
----------
100%|██████████| 938/938 [00:19<00:00, 47.15it/s]
Loss is 0.0026111400220543146,Train Accuracy is 0.951200008392334,Test Accuracy is 0.9601999521255493
Epoch:3/5
----------
100%|██████████| 938/938 [00:19<00:00, 47.28it/s]
Loss is 0.0020026741549372673,Train Accuracy is 0.9629499912261963,Test Accuracy is 0.9691999554634094
Epoch:4/5
----------
100%|██████████| 938/938 [00:19<00:00, 47.23it/s]
Loss is 0.001624452997930348,Train Accuracy is 0.9700999855995178,Test Accuracy is 0.9746999740600586