while-L

使用LSTM预测股票数据

数据集：股票数据集.

数据集来源：:https://www.kaggle.com/dsadads/databases

1 加载数据集

import numpy as np
import pandas as pd

import datetime

stock = pd.read_csv('dataset/SH600519.csv')

stock_data = pd.read_csv('dataset/SH600519.csv')
stock_data.set_index(['date'], inplace=True)

stock_data

	Unnamed: 0	open	close	high	low	volume	code
date
2010-04-26	74	88.702	87.381	89.072	87.362	107036.13	600519
2010-04-27	75	87.355	84.841	87.355	84.681	58234.48	600519
2010-04-28	76	84.235	84.318	85.128	83.597	26287.43	600519
2010-04-29	77	84.592	85.671	86.315	84.592	34501.20	600519
2010-04-30	78	83.871	82.340	83.871	81.523	85566.70	600519
...	...	...	...	...	...	...	...
2020-04-20	2495	1221.000	1227.300	1231.500	1216.800	24239.00	600519
2020-04-21	2496	1221.020	1200.000	1223.990	1193.000	29224.00	600519
2020-04-22	2497	1206.000	1244.500	1249.500	1202.220	44035.00	600519
2020-04-23	2498	1250.000	1252.260	1265.680	1247.770	26899.00	600519
2020-04-24	2499	1248.000	1250.560	1259.890	1235.180	19122.00	600519

2426 rows × 7 columns

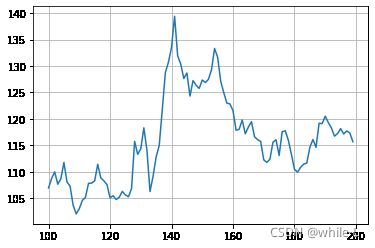
2 绘制收盘价图

import matplotlib.pyplot as plt
from matplotlib import ticker # 调整坐标轴
from matplotlib.pylab import date2num # 日期转换

stock = stock[100:200]

stock['close'].plot(grid = True)

3 计算涨跌幅

stock_data.shape[0]

stock_data.iloc[101:102,].values

array([[1.75000e+02, 1.06990e+02, 1.08749e+02, 1.08858e+02, 1.06475e+02,
        1.85480e+04, 6.00519e+05]])

quote_change = []
for i in range(stock_data.shape[0]):
    if (i == 0):
        quote_change.append(0)
    else:
        today = stock_data.iloc[(i,1)]
        yestaday = stock_data.iloc[(i-1,1)]
        quote = (today - yestaday)/yestaday
        quote_change.append(np.array(quote,dtype=np.float))

stock_data['quote_change'] = quote_change

stock_data

	Unnamed: 0	open	close	high	low	volume	code	quote_change
date
2010-04-26	74	88.702	87.381	89.072	87.362	107036.13	600519	0
2010-04-27	75	87.355	84.841	87.355	84.681	58234.48	600519	-0.015185677887758948
2010-04-28	76	84.235	84.318	85.128	83.597	26287.43	600519	-0.03571632991815013
2010-04-29	77	84.592	85.671	86.315	84.592	34501.20	600519	0.00423814328960645
2010-04-30	78	83.871	82.340	83.871	81.523	85566.70	600519	-0.008523264611310805
...	...	...	...	...	...	...	...	...
2020-04-20	2495	1221.000	1227.300	1231.500	1216.800	24239.00	600519	0.00909090909090909
2020-04-21	2496	1221.020	1200.000	1223.990	1193.000	29224.00	600519	1.6380016380001484e-05
2020-04-22	2497	1206.000	1244.500	1249.500	1202.220	44035.00	600519	-0.012301190807685363
2020-04-23	2498	1250.000	1252.260	1265.680	1247.770	26899.00	600519	0.03648424543946932
2020-04-24	2499	1248.000	1250.560	1259.890	1235.180	19122.00	600519	-0.0016

2426 rows × 8 columns

20天最大涨幅的计算

len(stock_data)

封装成函数

def up(min_data ,i , m):
    if(min_data > stock_data.iloc[i - m,1]):
        min_data = stock_data.iloc[i - m,1]
    return min_data
def down(min_data,i,k):
    if(min_data > stock_data.iloc[(i + k,1)]):
        min_data = stock_data.iloc[(i + k,1)]
    return min_data

sequence = 20

new_feature = []

for i in range(stock_data.shape[0]):
    min_data = stock_data.iloc[i,1]
    # 当i<10时，向上寻找i中最小值 向下寻找十天的最小值
    if (i < 10):
        for m in range(i):
            min_data = up(min_data ,i ,m)       
        for k in range(10):
            min_data = down(min_data,i,k)
    if (i > (stock.shape[0]-10)):                  
        for j in range(10):
            min_data = up(min_data ,i ,j)   
        for n in range(stock.shape[0]-i):   
            min_data = down(min_data,i,n) 
    else:
        for j in range(10):
            min_data = up(min_data,i,j)
        for k in range(10):
            min_data = down(min_data,i,k)
        
    new_feature.append(np.array((stock_data.iloc[(i,1)]-min_data)/min_data,dtype=np.float))

直接求

sequence = 20

new_feature = []

for i in range(stock_data.shape[0]):
    min_data = stock_data.iloc[i,1]
    # 当i<10时，向上寻找i中最小值 向下寻找十天的最小值
    if (i < 10):
        for m in range(i):
            if(min_data > stock_data.iloc[i-m,1]):
                min_data = stock_data.iloc[i-m,1]       
        for k in range(10):
            if(min_data > stock_data.iloc[(i + k,1)]):
                min_data = stock_data.iloc[(i + k,1)]
    if (i > (stock.shape[0]-10)):                  
        for j in range(10):
            if(min_data > stock_data.iloc[(i - j,1)]):
                min_data = stock_data.iloc[(i - j,1)]  
        for n in range(stock.shape[0]-i):   
             if(min_data > stock_data.iloc[(i + n,1)]):
                min_data = stock_data.iloc[(i + n,1)]  
    else:
        for j in range(10):
            if(min_data > stock_data.iloc[(i - j,1)]):
                min_data = stock_data.iloc[(i - j,1)]  
        for k in range(10):
            if(min_data > stock_data.iloc[(i + k,1)]):
                min_data = stock_data.iloc[(i + k,1)]
        
    new_feature.append(np.array((stock_data.iloc[(i,1)]-min_data)/min_data,dtype=np.float))

new_feature

len(new_feature)

stock_data['max_increase'] = new_feature

stock_data

	Unnamed: 0	open	close	high	low	volume	code	quote_change	max_increase
date
2010-04-26	74	88.702	87.381	89.072	87.362	107036.13	600519	0	0.10317637987214874
2010-04-27	75	87.355	84.841	87.355	84.681	58234.48	600519	-0.015185677887758948	0.08642389871402628
2010-04-28	76	84.235	84.318	85.128	83.597	26287.43	600519	-0.03571632991815013	0.0476208243165932
2010-04-29	77	84.592	85.671	86.315	84.592	34501.20	600519	0.00423814328960645	0.052060791483222554
2010-04-30	78	83.871	82.340	83.871	81.523	85566.70	600519	-0.008523264611310805	0.043093798970225965
...	...	...	...	...	...	...	...	...	...
2020-04-20	2495	1221.000	1227.300	1231.500	1216.800	24239.00	600519	0.00909090909090909	0.059895833333333336
2020-04-21	2496	1221.020	1200.000	1223.990	1193.000	29224.00	600519	1.6380016380001484e-05	0.05991319444444443
2020-04-22	2497	1206.000	1244.500	1249.500	1202.220	44035.00	600519	-0.012301190807685363	0.04155871074722759
2020-04-23	2498	1250.000	1252.260	1265.680	1247.770	26899.00	600519	0.03648424543946932	0.07955919438974668
2020-04-24	2499	1248.000	1250.560	1259.890	1235.180	19122.00	600519	-0.0016	0.07124463519313305

2426 rows × 9 columns

选择use_cols作为特征

#X.append(np.array(stock_data.iloc[i:(i+sequence),].values, dtype=np.float))
# label 取当前日期后的30天收盘价涨幅
#y.append(np.array(stock_data.iloc[(i + sequence,5)],dtype=np.float))

4 归一化

sklearn

from sklearn.preprocessing import MinMaxScaler

# stock_data = stock_data[2000:2420]

columns = ['open','close','high','low','volume','quote_change','max_increase']
stock_data = stock_data[columns]

stock_data

	open	close	high	low	volume	quote_change	max_increase
date
2010-04-26	88.702	87.381	89.072	87.362	107036.13	0	0.10317637987214874
2010-04-27	87.355	84.841	87.355	84.681	58234.48	-0.015185677887758948	0.08642389871402628
2010-04-28	84.235	84.318	85.128	83.597	26287.43	-0.03571632991815013	0.0476208243165932
2010-04-29	84.592	85.671	86.315	84.592	34501.20	0.00423814328960645	0.052060791483222554
2010-04-30	83.871	82.340	83.871	81.523	85566.70	-0.008523264611310805	0.043093798970225965
...	...	...	...	...	...	...	...
2020-04-20	1221.000	1227.300	1231.500	1216.800	24239.00	0.00909090909090909	0.059895833333333336
2020-04-21	1221.020	1200.000	1223.990	1193.000	29224.00	1.6380016380001484e-05	0.05991319444444443
2020-04-22	1206.000	1244.500	1249.500	1202.220	44035.00	-0.012301190807685363	0.04155871074722759
2020-04-23	1250.000	1252.260	1265.680	1247.770	26899.00	0.03648424543946932	0.07955919438974668
2020-04-24	1248.000	1250.560	1259.890	1235.180	19122.00	-0.0016	0.07124463519313305

2426 rows × 7 columns

scaler = MinMaxScaler()
stock_scaler = scaler.fit_transform(stock_data)

stock_scaler = pd.DataFrame(stock_scaler)
stock_scaler.columns = columns

stock_scaler

	open	close	high	low	volume	quote_change	max_increase
0	0.007093	0.005806	0.006509	0.006230	0.353556	0.436961	0.299871
1	0.005941	0.003638	0.005059	0.003934	0.180317	0.378208	0.251182
2	0.003274	0.003192	0.003179	0.003006	0.066909	0.298776	0.138405
3	0.003579	0.004347	0.004181	0.003858	0.096067	0.453358	0.151309
4	0.002963	0.001504	0.002118	0.001230	0.277342	0.403985	0.125247
...	...	...	...	...	...	...	...
2421	0.975205	0.978697	0.971139	0.973477	0.059637	0.472133	0.174081
2422	0.975222	0.955397	0.964798	0.953095	0.077333	0.437024	0.174131
2423	0.962380	0.993377	0.986338	0.960991	0.129910	0.389368	0.120786
2424	1.000000	1.000000	1.000000	1.000000	0.069080	0.578117	0.231230
2425	0.998290	0.998549	0.995111	0.989218	0.041473	0.430770	0.207065

2426 rows × 7 columns

# 为了归一化后复现原来数据
close_min = stock_data['quote_change'].min()
close_max = stock_data['quote_change'].max()
# 归一化处理（0，1）
stock=stock_data.apply(lambda x:(x-min(x))/(max(x)-min(x)))
stock

	open	close	high	low	volume	quote_change	max_increase
date
2010-04-26	0.007093	0.005806	0.006509	0.006230	0.353556	0.436961	0.299871
2010-04-27	0.005941	0.003638	0.005059	0.003934	0.180317	0.378208	0.251182
2010-04-28	0.003274	0.003192	0.003179	0.003006	0.066909	0.298776	0.138405
2010-04-29	0.003579	0.004347	0.004181	0.003858	0.096067	0.453358	0.151309
2010-04-30	0.002963	0.001504	0.002118	0.001230	0.277342	0.403985	0.125247
...	...	...	...	...	...	...	...
2020-04-20	0.975205	0.978697	0.971139	0.973477	0.059637	0.472133	0.174081
2020-04-21	0.975222	0.955397	0.964798	0.953095	0.077333	0.437024	0.174131
2020-04-22	0.962380	0.993377	0.986338	0.960991	0.129910	0.389368	0.120786
2020-04-23	1.000000	1.000000	1.000000	1.000000	0.069080	0.578117	0.23123
2020-04-24	0.998290	0.998549	0.995111	0.989218	0.041473	0.43077	0.207065

2426 rows × 7 columns

5 前20天的数据预测之后的数据

stock = stock_scaler

pd.DataFrame(stock.iloc[201:400,].values)

	0	1	2	3	4	5	6
0	0.029674	0.029436	0.029161	0.029494	0.055448	0.424231	0.000000
1	0.029393	0.028650	0.028655	0.028507	0.087525	0.425903	0.000000
2	0.028881	0.027435	0.028486	0.027811	0.107546	0.416771	0.000000
3	0.027631	0.027946	0.027448	0.027674	0.091984	0.387424	0.000000
4	0.028094	0.028743	0.027856	0.028413	0.092701	0.455529	0.013949
...	...	...	...	...	...	...	...
194	0.051861	0.051945	0.051049	0.052022	0.028754	0.380821	0.000000
195	0.051450	0.052410	0.052271	0.051808	0.038700	0.423796	0.000000
196	0.051830	0.050992	0.051593	0.051102	0.026645	0.449180	0.009179
197	0.052522	0.054592	0.053468	0.052875	0.082392	0.459155	0.025905
198	0.054341	0.054115	0.053112	0.053678	0.063958	0.495008	0.069899

199 rows × 7 columns

stock

	open	close	high	low	volume	quote_change	max_increase
0	0.007093	0.005806	0.006509	0.006230	0.353556	0.436961	0.299871
1	0.005941	0.003638	0.005059	0.003934	0.180317	0.378208	0.251182
2	0.003274	0.003192	0.003179	0.003006	0.066909	0.298776	0.138405
3	0.003579	0.004347	0.004181	0.003858	0.096067	0.453358	0.151309
4	0.002963	0.001504	0.002118	0.001230	0.277342	0.403985	0.125247
...	...	...	...	...	...	...	...
2421	0.975205	0.978697	0.971139	0.973477	0.059637	0.472133	0.174081
2422	0.975222	0.955397	0.964798	0.953095	0.077333	0.437024	0.174131
2423	0.962380	0.993377	0.986338	0.960991	0.129910	0.389368	0.120786
2424	1.000000	1.000000	1.000000	1.000000	0.069080	0.578117	0.231230
2425	0.998290	0.998549	0.995111	0.989218	0.041473	0.430770	0.207065

2426 rows × 7 columns

# 序列长度为30，即用前一个月的数据预测之后一天的数据
sequence = 20

X = []
y = []
label = []

for i in range(stock.shape[0]-sequence):
    # 选择use_cols作为特征
    X.append(np.array(stock.iloc[i:(i+sequence),].values, dtype=np.float))
    # 选择20天收盘价涨幅
    y.append(np.array(stock.iloc[(i+sequence),5],dtype=np.float))

len(X) , len(X[1])

(2406, 20)

len(y)

划分数据集

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.2,random_state=42)

len(X_train)

len(X_test)

import torch
import torch.utils.data as Data 
torch.manual_seed(1)

# list -> numpy
X_train = np.array(X_train)
y_train = np.array(y_train)
X_test = np.array(X_test)
y_test = np.array(y_test)

# numpy -> torch
X_train = torch.from_numpy(X_train)
y_train = torch.from_numpy(y_train)
X_test = torch.from_numpy(X_test)
y_test = torch.from_numpy(y_test)

print('X_train size: ', X_train.size())
print('y_train size: ', y_train.size())
print('X_test size: ', X_test.size())
print('y_test size: ', y_test.size())

X_train size:  torch.Size([1924, 20, 7])
y_train size:  torch.Size([1924])
X_test size:  torch.Size([482, 20, 7])
y_test size:  torch.Size([482])

6 定义网络模型

#  批处理 batch的大小为32
train_data = Data.TensorDataset(X_train, y_train)
test_data = Data.TensorDataset(X_test, y_test)

train_loader = Data.DataLoader(
    dataset=train_data,
    batch_size=32,
    shuffle=True,
    num_workers=2
)

test_loader = Data.DataLoader(
    dataset=test_data,
    batch_size=32,
    shuffle=True,
    num_workers=2
)

input_size = 7
seq_len = 20
hidden_size = 32
output_size = 1
import torch.nn as nn
import torch.nn.functional as F 
from torch.autograd import Variable
class MyNet(nn.Module):  
    def __init__(self, input_size=input_size, hidden_size=hidden_size, output_size=output_size):
        super(MyNet, self).__init__()
        self.input_size = input_size
        self.hidden_size = hidden_size
        self.output_size = output_size
        self.lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_size, batch_first=True)
        self.fc = nn.Linear(self.hidden_size*seq_len, self.output_size)            
    def forward(self, input):
        out,_ = self.lstm(input)
        b, s, h = out.size()
        out = self.fc(out.reshape(b, s*h))
        return out 

net = MyNet()
print(net)

MyNet(
  (lstm): LSTM(7, 32, batch_first=True)
  (fc): Linear(in_features=640, out_features=1, bias=True)
)

7 选择损失函数和优化器

import torch.optim as optim 
from tqdm import tqdm

loss_function = nn.MSELoss()
optimizer = optim.Adam(net.parameters(), lr=0.01)

for epoch in tqdm(range(100)):
    total_loss = 0
    for _,(data, label) in enumerate(train_loader):
        data = Variable(data).float()
        pred = net(data)
        label = Variable(label).float()
        label = label.unsqueeze(1)
        loss = loss_function(pred, label)
        loss.backward()
        optimizer.step()
        optimizer.zero_grad()
        total_loss += loss.item()
        
    if (epoch + 1) % 10 == 0:
        print('Epoch: ', epoch+1, ' loss: ', total_loss)

 10%|████████                                                                         | 10/100 [00:15<02:20,  1.56s/it]

Epoch:  10  loss:  0.39631053362973034


 20%|████████████████▏                                                                | 20/100 [00:30<01:59,  1.49s/it]

Epoch:  20  loss:  0.38432611781172454


 30%|████████████████████████▎                                                        | 30/100 [00:46<01:48,  1.56s/it]

Epoch:  30  loss:  0.3594463015906513


 40%|████████████████████████████████▍                                                | 40/100 [01:02<01:37,  1.62s/it]

Epoch:  40  loss:  0.2304799237754196


 50%|████████████████████████████████████████▌                                        | 50/100 [01:17<01:17,  1.55s/it]

Epoch:  50  loss:  0.19538419507443905


 60%|████████████████████████████████████████████████▌                                | 60/100 [01:33<01:06,  1.66s/it]

Epoch:  60  loss:  0.15910959872417152


 70%|████████████████████████████████████████████████████████▋                        | 70/100 [01:50<00:51,  1.73s/it]

Epoch:  70  loss:  0.10108215303625911


 80%|████████████████████████████████████████████████████████████████▊                | 80/100 [02:07<00:32,  1.63s/it]

Epoch:  80  loss:  0.09773806459270418


 90%|████████████████████████████████████████████████████████████████████████▉        | 90/100 [02:23<00:16,  1.67s/it]

Epoch:  90  loss:  0.06839053201838396


100%|████████████████████████████████████████████████████████████████████████████████| 100/100 [02:41<00:00,  1.62s/it]

Epoch:  100  loss:  0.06617061665747315

8 测试

pred_list = []
label_list = []

for _, (data, label) in enumerate(test_loader):
    data = Variable(data).float()
    pred = net(data)
    pred_list.extend(pred.data.squeeze(1).tolist())
    label_list.extend(label.tolist())

pred_list[:5]

[0.4532894492149353,
 0.4373990297317505,
 0.4552455246448517,
 0.3734513521194458,
 0.4417729675769806]

len(pred_list)

label_list[:5]

[0.4526440093601085,
 0.4235539693300972,
 0.4670736837074137,
 0.3081553795002458,
 0.5096712136068774]

9 可视化

import matplotlib.pyplot as plt  
plt.rcParams['font.sans-serif'] = [u'SimHei']
plt.rcParams['axes.unicode_minus'] = False

import matplotlib.pyplot as plt 

plt.figure(figsize=(20,6))

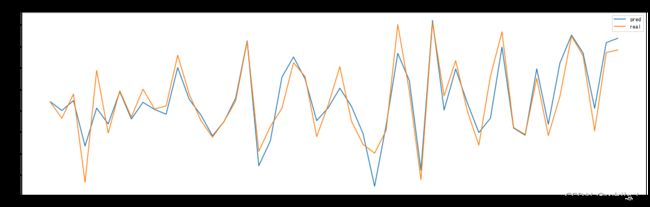
plt.plot([i*(close_max-close_min)+close_min for i in pred_list[:50]] , label='pred')
plt.plot([i*(close_max-close_min)+close_min for i in label_list[:50]], label='real')
plt.title('Stock Forecast(前50条数据)')
plt.legend()
plt.show()

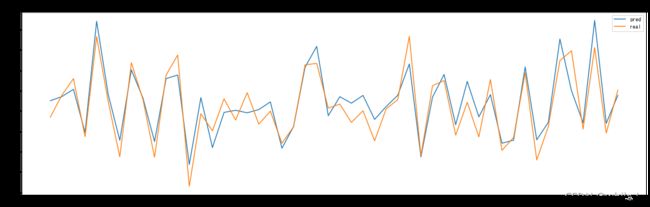
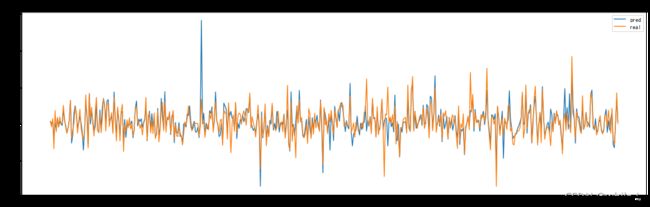
import matplotlib.pyplot as plt 
plt.figure(figsize=(20,6))
plt.plot([i*(close_max-close_min)+close_min for i in pred_list[50:100]] , label='pred')
plt.plot([i*(close_max-close_min)+close_min for i in label_list[50:100]], label='real')
plt.title('Stock Forecast')
plt.legend()
plt.show()

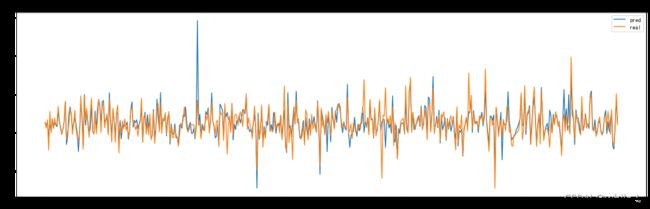
import matplotlib.pyplot as plt 

plt.figure(figsize=(20,6))
plt.plot(pred_list[400:480] , label='pred')
plt.plot(label_list[400:480], label='real')
plt.title('Stock Forecast（第400条到第480条数据）')
plt.legend()
plt.savefig('dataset/some.jpg')
plt.show()

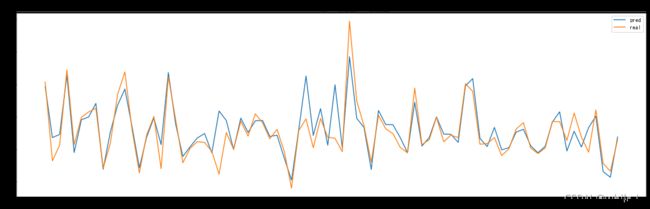
import matplotlib.pyplot as plt 
plt.figure(figsize=(20,6))
plt.plot(pred_list , label='pred')
plt.plot(label_list, label='real')
plt.title('Stock Forecast(测试集所有数据)')
plt.legend()
plt.savefig('dataset/pred_real.jpg')
plt.show()

import matplotlib.pyplot as plt 
plt.figure(figsize=(20,6))
plt.plot([i*(close_max-close_min)+close_min for i in pred_list[:482]] , label='pred')
plt.plot([i*(close_max-close_min)+close_min for i in label_list[:482]], label='real')
plt.title('Stock Forecast(测试集所有数据（还原数据）)')
plt.legend()
plt.savefig('dataset/all.jpg')
plt.show()

10 保存图片

import matplotlib.pyplot as plt 
plt.figure(figsize=(20,6))
plt.plot([i*(close_max-close_min)+close_min for i in pred_list[:482]] , label='pred')
plt.title('Stock Forecast pred')
plt.legend()
plt.savefig('dataset/pred.jpg')
plt.show()

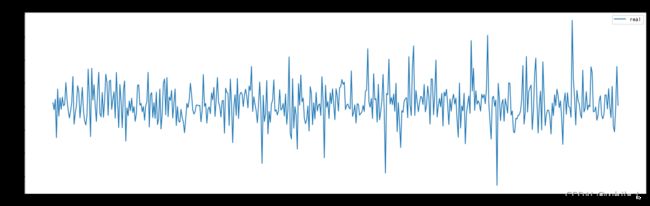
import matplotlib.pyplot as plt 
plt.figure(figsize=(20,6))
plt.plot([i*(close_max-close_min)+close_min for i in label_list[:482]], label='real')
plt.title('Stock Forecast （real）')
plt.legend()
plt.savefig('dataset/real.jpg')
plt.show()

11 计算相似度

len(label_list)

欧式距离

sum_all = 0
for i in range(len(label_list)):
    sum_all = sum_all + (label_list[i] - pred_list[i])**2

sum_all

1.1392427957537818

DTW

pred_some = pred_list[50:100]
label_some = label_list[50:100]

pred_some = pred_list[:482]
label_some = label_list[0:482]

欧式距离矩阵

distances = np.zeros((len(pred_some), len(pred_some)))
for i in range(len(pred_some)):
    for j in range(len(label_some)):
        distances[i,j] = (label_some[j]-pred_some[i])**2

len(distances)

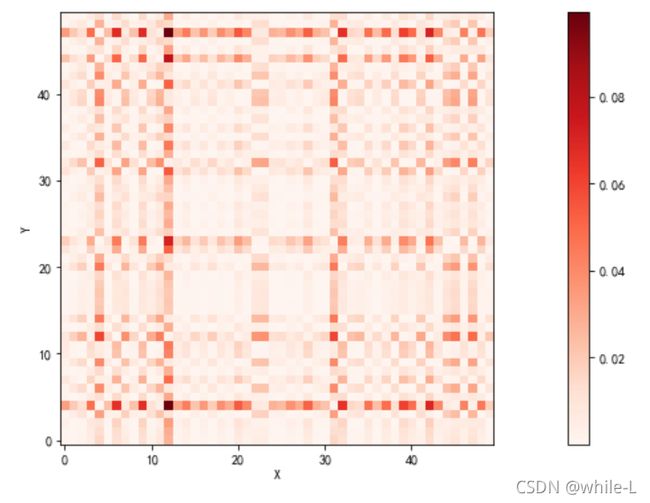
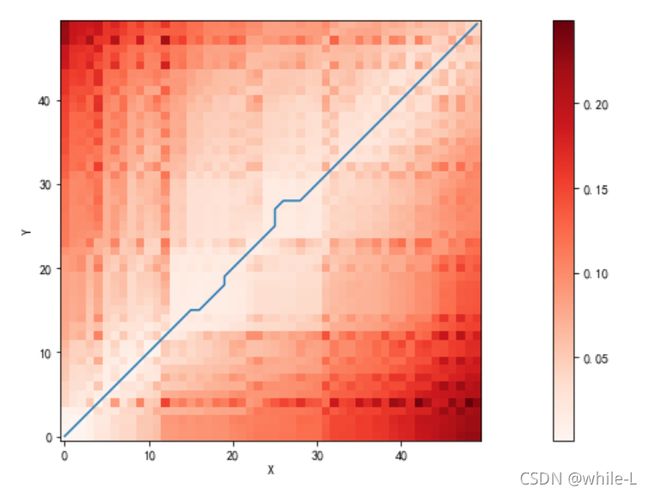
计算两个序列的距离矩阵。横着表示x序列，竖着是y序列。
比如说第0行第0个元素1表示x序列的第0个值和y序列的第0个值的距离（Python的索引从0开始）

颜色越深表示距离越远

欧式距离矩阵可视化

def distance_cost_plot(distances):
    plt.figure(figsize=(20,6))
    plt.imshow(distances, interpolation='nearest', cmap='Reds') 
    plt.gca().invert_yaxis()#倒转y轴，让它与x轴的都从左下角开始
    plt.xlabel("X")
    plt.ylabel("Y")
#    plt.grid()
    plt.colorbar()
distance_cost_plot(distances)

x = pred_some
y = label_some

# 计算一个累积距离矩阵
accumulated_cost = np.zeros((len(pred_some), len(label_some)))
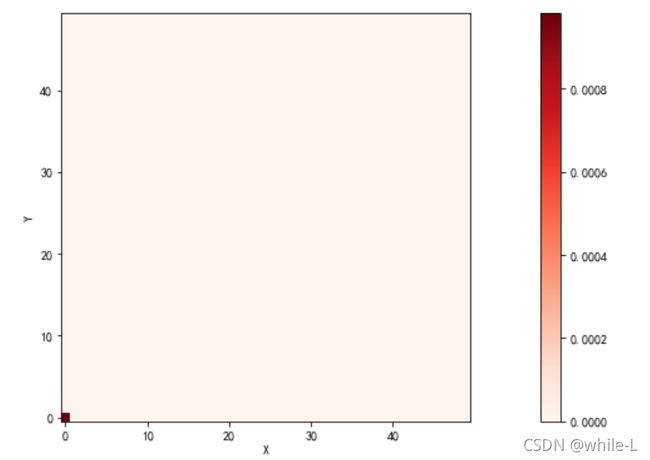
accumulated_cost[0,0] = distances[0,0]

pd.DataFrame(accumulated_cost)

	0	1	2	3	4	5	6	7	8	9	...	472	473	474	475	476	477	478	479	480	481
0	4.165926e-07	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
1	0.000000e+00	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
2	0.000000e+00	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
3	0.000000e+00	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
4	0.000000e+00	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
477	0.000000e+00	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
478	0.000000e+00	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
479	0.000000e+00	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
480	0.000000e+00	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
481	0.000000e+00	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0

482 rows × 482 columns

distance_cost_plot(accumulated_cost)

显然累积距离矩阵的第0行第0列=距离矩阵的第0行第0列=1，我们必须经过起点吧……如果我们一直往右走，那么累积距离距离矩阵

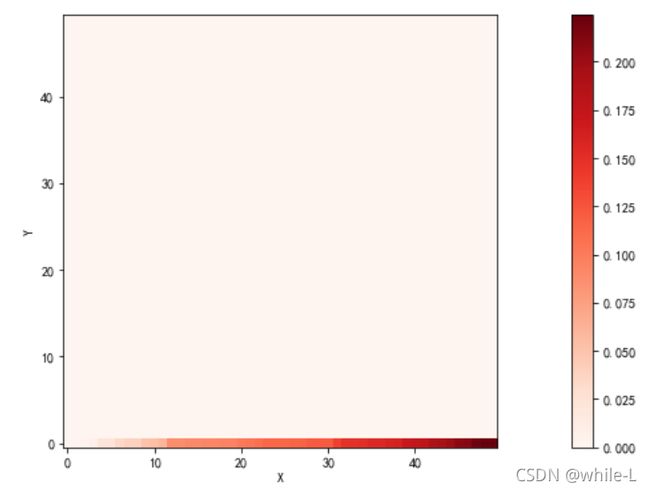
# 累积距离距离矩阵
for i in range(1, len(label_some)):
    accumulated_cost[0,i] = distances[0,i] + accumulated_cost[0, i-1]

pd.DataFrame(accumulated_cost)

	0	1	2	3	4	5	6	7	8	9	...	472	473	474	475	476	477	478	479	480	481
0	4.165926e-07	0.000885	0.001075	0.022139	0.025317	0.028503	0.028894	0.029663	0.030173	0.030348	...	2.791318	2.794677	2.794919	2.798835	2.803386	2.812828	2.827525	2.828109	2.850578	2.850708
1	0.000000e+00	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
2	0.000000e+00	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
3	0.000000e+00	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
4	0.000000e+00	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
477	0.000000e+00	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
478	0.000000e+00	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
479	0.000000e+00	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
480	0.000000e+00	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
481	0.000000e+00	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000

482 rows × 482 columns

distance_cost_plot(accumulated_cost)

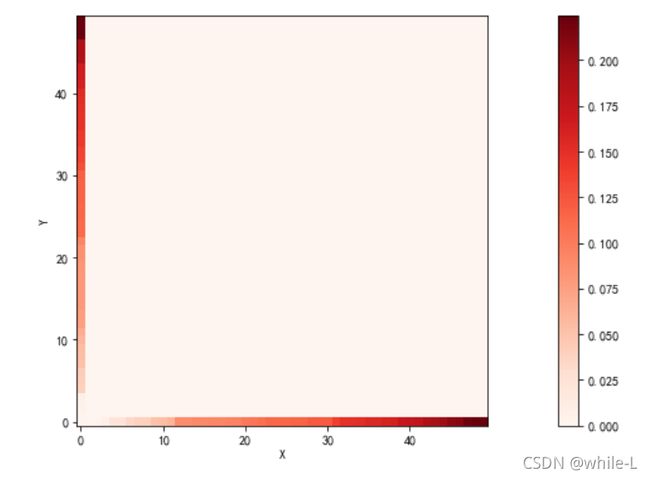
如果我们一直往上走，那么

for i in range(1, len(pred_some)):
    accumulated_cost[i,0] = distances[i, 0] + accumulated_cost[i-1, 0]

pd.DataFrame(accumulated_cost)

	0	1	2	3	4	5	6	7	8	9	...	472	473	474	475	476	477	478	479	480	481
0	4.165926e-07	0.000885	0.001075	0.022139	0.025317	0.028503	0.028894	0.029663	0.030173	0.030348	...	2.791318	2.794677	2.794919	2.798835	2.803386	2.812828	2.827525	2.828109	2.850578	2.850708
1	2.328260e-04	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
2	2.395939e-04	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
3	6.511071e-03	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
4	6.629250e-03	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
477	2.676938e+00	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
478	2.696313e+00	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
479	2.696541e+00	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
480	2.709715e+00	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
481	2.709716e+00	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000

482 rows × 482 columns

distance_cost_plot(accumulated_cost)

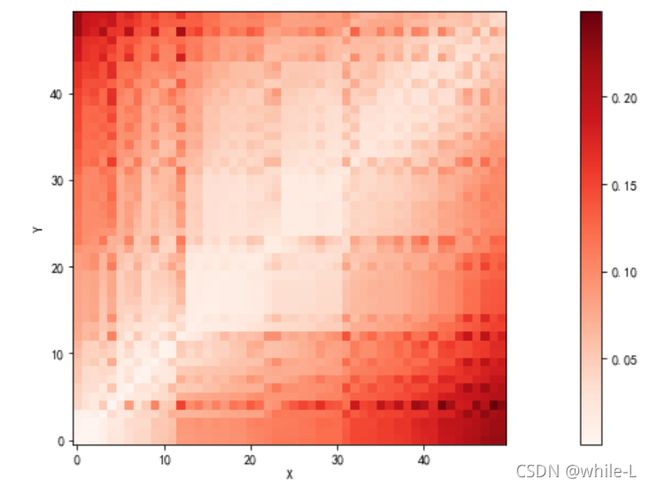
把累积距离矩阵计算完整

for i in range(1, len(pred_some)):
    for j in range(1, len(label_some)):
        accumulated_cost[i, j] = min(accumulated_cost[i-1, j-1], accumulated_cost[i-1, j], accumulated_cost[i, j-1]) + distances[i, j]

pd.DataFrame(accumulated_cost)

	0	1	2	3	4	5	6	7	8	9	...	472	473	474	475	476	477	478	479	480	481
0	4.165926e-07	0.000885	0.001075	0.022139	0.025317	0.028503	0.028894	0.029663	0.030173	0.030348	...	2.791318	2.794677	2.794919	2.798835	2.803386	2.812828	2.827525	2.828109	2.850578	2.850708
1	2.328260e-04	0.000192	0.001073	0.017777	0.023000	0.024644	0.025915	0.026055	0.027535	0.027542	...	2.784774	2.790229	2.790229	2.792408	2.799356	2.805962	2.817059	2.817128	2.844613	2.844633
2	2.395939e-04	0.001196	0.000332	0.021968	0.020739	0.024149	0.024466	0.025348	0.025773	0.026003	...	2.757107	2.760244	2.760550	2.764715	2.769005	2.778831	2.794007	2.794689	2.816575	2.816754
3	6.511071e-03	0.002750	0.009097	0.004596	0.023151	0.021286	0.031205	0.027180	0.035836	0.030210	...	2.759153	2.776096	2.764378	2.760848	2.782545	2.769306	2.771019	2.774119	2.826897	2.821256
4	6.629250e-03	0.003082	0.003390	0.021244	0.009206	0.011224	0.012202	0.012465	0.013627	0.013630	...	2.710571	2.715399	2.715415	2.718022	2.724259	2.731596	2.743634	2.743794	2.769848	2.769848
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
477	2.676938e+00	2.670701	2.651317	2.633292	2.665250	2.625748	2.589558	2.560992	2.560040	2.527341	...	0.777889	0.798232	0.777122	0.773360	0.805854	0.770449	0.770450	0.780098	0.854235	0.798668
478	2.696313e+00	2.682825	2.674917	2.633320	2.671796	2.632704	2.615029	2.573559	2.586418	2.543372	...	0.790750	0.817015	0.792572	0.779330	0.816334	0.772270	0.770795	0.783832	0.864046	0.815159
479	2.696541e+00	2.683021	2.675789	2.650064	2.638521	2.634361	2.616289	2.573703	2.575026	2.543378	...	0.790865	0.796182	0.792572	0.781524	0.786252	0.778901	0.781925	0.770866	0.798300	0.798319
480	2.709715e+00	2.703718	2.685858	2.717282	2.641856	2.663456	2.625196	2.593830	2.582086	2.559598	...	0.810622	0.794020	0.809387	0.812749	0.783702	0.823548	0.834297	0.789990	0.772145	0.787908
481	2.709716e+00	2.704500	2.686100	2.706414	2.645237	2.644846	2.625659	2.594505	2.582678	2.559730	...	0.795156	0.797587	0.794210	0.797908	0.788494	0.792804	0.807078	0.790492	0.795145	0.772238

482 rows × 482 columns

distance_cost_plot(accumulated_cost)

现在，最佳路径已经清晰地显示在了累积距离矩阵之中，就是图中颜色最淡的方块。

现在，我们只需要通过回溯的方法找回最佳路径就可以了：

path = [[len(label_some)-1, len(pred_some)-1]]
i = len(pred_some)-1
j = len(label_some)-1
while i>0 and j>0:
    if i==0:
        j = j - 1
    elif j==0:
        i = i - 1
    else:
        if accumulated_cost[i-1, j] == min(accumulated_cost[i-1, j-1], accumulated_cost[i-1, j], accumulated_cost[i, j-1]):
            i = i - 1#来自于左边
        elif accumulated_cost[i, j-1] == min(accumulated_cost[i-1, j-1], accumulated_cost[i-1, j], accumulated_cost[i, j-1]):
            j = j-1#来自于下边
        else:
            i = i - 1#来自于左下边
            j= j- 1
    path.append([j, i])
path.append([0,0])

path_x = [point[0] for point in path]
path_y = [point[1] for point in path]
distance_cost_plot(accumulated_cost)
plt.plot(path_x, path_y)

[]

图片相似度

from skimage.metrics import structural_similarity as sk_cpt_ssim

import matplotlib.pyplot as plt
import numpy as np
import cv2

def mse(imageA, imageB):
    # 计算两张图片的MSE指标
    err = np.sum((imageA.astype("float") - imageB.astype("float")) ** 2)
    err /= float(imageA.shape[0] * imageA.shape[1])
    
    # 返回结果，该值越小越好
    return err

def compare_images(imageA, imageB, title):
    # 分别计算输入图片的MSE和SSIM指标值的大小
    m = mse(imageA, imageB)
    s = sk_cpt_ssim(imageA, imageB)

    # 创建figure
    fig = plt.figure(title)
    plt.suptitle("MSE: %.2f, SSIM: %.2f" % (m, s))

    # 显示第一张图片
    ax = fig.add_subplot(1, 2, 1)
    plt.imshow(imageA, cmap = plt.cm.gray)
    plt.axis("off")

    # 显示第二张图片
    ax = fig.add_subplot(1, 2, 2)
    plt.imshow(imageB, cmap = plt.cm.gray)
    plt.axis("off")
    plt.tight_layout()
    plt.show()



# 读取图片
pred_image = cv2.imread("dataset/pred.jpg")
real_image = cv2.imread("dataset/real.jpg")
all_image = cv2.imread('dataset/all.jpg')
some_image = cv2.imread('dataset/some.jpg')

# 将彩色图转换为灰度图
pred = cv2.cvtColor(pred_image, cv2.COLOR_BGR2GRAY)
real = cv2.cvtColor(real_image, cv2.COLOR_BGR2GRAY)
all_image = cv2.cvtColor(all_image,cv2.COLOR_BGR2GRAY)
some_image = cv2.cvtColor(some_image,cv2.COLOR_BGR2GRAY)

# 初始化figure对象
fig = plt.figure("Images")
# images = ("pred", pred), ("real", real),('all',all_image),('some',some_image)
images = ("pred", pred), ("real", real)

# 遍历每张图片
for (i, (name, image)) in enumerate(images):
    # 显示图片
    ax = fig.add_subplot(1, 4, i + 1)
    ax.set_title(name)
    plt.imshow(image, cmap = plt.cm.gray)
    plt.axis("off")
plt.tight_layout()
plt.show()

# 比较图片
# compare_images(real, real, "real vs real")
compare_images(real, pred, "real vs pred")
# compare_images(all_image, pred, "real vs pred")
# compare_images(some_image,all_image,'some vs all')

你可能感兴趣的:(python)

理解Gunicorn：Python WSGI服务器的基石范范0825 ipython linux 运维
理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
Python数据分析与可视化实战指南 William数据分析 python python 数据
在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
python os.environ 江湖偌大 python 深度学习
os.environ['TF_CPP_MIN_LOG_LEVEL']='0'#默认值，输出所有信息os.environ['TF_CPP_MIN_LOG_LEVEL']='1'#屏蔽通知信息（INFO）os.environ['TF_CPP_MIN_LOG_LEVEL']='2'#屏蔽通知信息和警告信息（INFO\WARNING）os.environ['TF_CPP_MIN_LOG_LEVEL']='
Python中os.environ基本介绍及使用方法鹤冲天Pro #Python python 服务器开发语言
文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
Pyecharts数据可视化大屏：打造沉浸式数据分析体验我的运维人生信息可视化数据分析数据挖掘运维开发技术共享
Pyecharts数据可视化大屏：打造沉浸式数据分析体验在当今这个数据驱动的时代，如何将海量数据以直观、生动的方式展现出来，成为了数据分析师和企业决策者关注的焦点。Pyecharts，作为一款基于Python的开源数据可视化库，凭借其丰富的图表类型、灵活的配置选项以及高度的定制化能力，成为了构建数据可视化大屏的理想选择。本文将深入探讨如何利用Pyecharts打造数据可视化大屏，并通过实际代码案例
Python教程：一文了解使用Python处理XPath 旦莫 Python进阶 python 开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath？2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
python os.environ_python os.environ 读取和设置环境变量 weixin_39605414 python os.environ
>>>importos>>>os.environ.keys()['LC_NUMERIC','GOPATH','GOROOT','GOBIN','LESSOPEN','SSH_CLIENT','LOGNAME','USER','HOME','LC_PAPER','PATH','DISPLAY','LANG','TERM','SHELL','J2REDIR','LC_MONETARY','QT_QPA
使用Faiss进行高效相似度搜索 llzwxh888 faiss python
在现代AI应用中，快速和高效的相似度搜索是至关重要的。Faiss（FacebookAISimilaritySearch）是一个专门用于快速相似度搜索和聚类的库，特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索，并结合Python代码演示其基本用法。什么是Faiss？Faiss是一个由FacebookAIResearch团队开发的开源库，主要用于高维向量的相似性搜索和聚类。Faiss
python是什么意思中文-在python中%是什么意思编程大乐趣
Python中%有两种：1、数值运算：%代表取模，返回除法的余数。如：>>>7%212、%操作符（字符串格式化，stringformatting），说明如下：%[(name)][flags][width].[precision]typecode(name)为命名flags可以有+，-，''或0。+表示右对齐。-表示左对齐。''为一个空格，表示在正数的左侧填充一个空格，从而与负数对齐。0表示使用0填
Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Python python 开发语言大数据数据分析数据挖掘
大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
python八股文面试题分享及解析(1) Shawn________ python
#1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果：21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型，不仅仅改变
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
Python快速入门 —— 第三节：类与对象孤华暗香 Python快速入门 python 开发语言
第三节：类与对象目标：了解面向对象编程的基础概念，并学会如何定义类和创建对象。内容：类与对象：定义类：class关键字。类的构造函数：__init__()。类的属性和方法。对象的创建与使用。示例：classStudent:def__init__(self,name,age,major):self.name&#
pyecharts——绘制柱形图折线图 2224070247 信息可视化 python java 数据可视化
一、pyecharts概述自2013年6月百度EFE(ExcellentFrontEnd）数据可视化团队研发的ECharts1.0发布到GitHub网站以来，ECharts一直备受业界权威的关注并获得广泛好评，成为目前成熟且流行的数据可视化图表工具，被应用到诸多数据可视化的开发领域。Python作为数据分析领域最受欢迎的语言，也加入ECharts的使用行列，并研发出方便Python开发者使用的数据
Python 实现图片裁剪（附代码） | Python工具剑客阿良_ALiang
前言本文提供将图片按照自定义尺寸进行裁剪的工具方法，一如既往的实用主义。环境依赖ffmpeg环境安装，可以参考我的另一篇文章：windowsffmpeg安装部署_阿良的博客-CSDN博客本文主要使用到的不是ffmpeg，而是ffprobe也在上面这篇文章中的zip包中。ffmpy安装：pipinstallffmpy-ihttps://pypi.douban.com/simple代码不废话了，上代码
【华为OD技术面试真题 - 技术面】- python八股文真题题库（4) 算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例：文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片（Slicing）操作**基本切片语法
python os 环境变量 CV矿工 python 开发语言 numpy
环境变量：环境变量是程序和操作系统之间的通信方式。有些字符不宜明文写进代码里，比如数据库密码，个人账户密码，如果写进自己本机的环境变量里，程序用的时候通过os.environ.get（）取出来就行了。os.environ是一个环境变量的字典。环境变量的相关操作importos"""设置/修改环境变量：os.environ[‘环境变量名称’]=‘环境变量值’#其中key和value均为string类
Python爬虫解析工具之xpath使用详解 eqa11 python 爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中，数据提取是一个至关重要的环节。xpath作为一门
【华为OD技术面试真题 - 技术面】- python八股文真题题库（1）算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.数据预处理流程数据预处理的主要步骤工具和库2.介绍线性回归、逻辑回归模型线性回归（LinearRegression）模型形式：关键点：逻辑回归（LogisticRegression）模型形式：关键点：参数估计与评估：3.python浅拷贝及深拷贝浅拷贝（Shal
nosql数据库技术与应用知识点皆过客，揽星河 NoSQL nosql 数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
《Python数据分析实战终极指南》 xjt921122 python 数据分析开发语言
对于分析师来说，大家在学习Python数据分析的路上，多多少少都遇到过很多大坑**，有关于技能和思维的**：Excel已经没办法处理现有的数据量了，应该学Python吗？找了一大堆Python和Pandas的资料来学习，为什么自己动手就懵了？跟着比赛类公开数据分析案例练了很久，为什么当自己面对数据需求还是只会数据处理而没有分析思路？学了对比、细分、聚类分析，也会用PEST、波特五力这类分析法，为啥
Python中深拷贝与浅拷贝的区别 yuxiaoyu.
转自：http://blog.csdn.net/u014745194/article/details/70271868定义：在Python中对象的赋值其实就是对象的引用。当创建一个对象，把它赋值给另一个变量的时候，python并没有拷贝这个对象，只是拷贝了这个对象的引用而已。浅拷贝：拷贝了最外围的对象本身，内部的元素都只是拷贝了一个引用而已。也就是，把对象复制一遍，但是该对象中引用的其他对象我不复
Python开发常用的三方模块如下：换个网名有点难 python 开发语言
Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
Python编译器鹿鹿~ Python编译器 Python python 开发语言后端
嘿嘿嘿我又来了啊有些小盆友可能不知道Python其实是有编译器的，也就是PyCharm。你们可能会问到这个是干嘛的又不可以吃也不可以穿好像没有什么用，其实你还说对了这个还真的不可以吃也不可以穿，但是它用来干嘛的呢。用来编译你所打出的代码进行运行（可能这里说的有点不对但是只是个人认为）现在我们来说说PyCharm是用来干嘛的。PyCharm是一种PythonIDE，带有一整套可以帮助用户在使用Pyt
一文掌握python面向对象魔术方法（二）程序员neil python python 开发语言
接上篇：一文掌握python面向对象魔术方法（一）-CSDN博客目录六、迭代和序列化：1、__iter__(self):定义迭代器，使得类可以被for循环迭代。2、__getitem__(self,key):定义索引操作，如obj[key]。3、__setitem__(self,key,value):定义赋值操作，如obj[key]=value。4、__delitem__(self,key):定义
一文掌握python常用的list（列表）操作程序员neil python python 开发语言
目录一、创建列表1.直接创建列表：2.使用list()构造器3.使用列表推导式4.创建空列表二、访问列表元素1.列表支持通过索引访问元素，索引从0开始：2.还可以使用切片操作访问列表的一部分：三、修改列表元素四、添加元素1.append()：在末尾添加元素2.insert()：在指定位置插入元素五、删除元素1.del：删除指定位置的元素2.remove()：删除指定值的第一个匹配项3.pop()：
Python实现简单的机器学习算法 master_chenchengg python python 办公效率 python开发 IT
Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
python中的深拷贝与浅拷贝 anshejd70787 python
深拷贝和浅拷贝浅拷贝的时候，修改原来的对象，浅拷贝的对象不会发生改变。1、对象的赋值对象的赋值实际上是对象之间的引用：当创建一个对象，然后将这个对象赋值给另外一个变量的时候，python并没有拷贝这个对象，而只是拷贝了这个对象的引用。当对对象做赋值或者是参数传递或者作为返回值的时候，总是传递原始对象的引用，而不是一个副本。如下所示：>>>aList=["kel","abc",123]>>>bLis
用Python实现简单的猜数字游戏程序媛了了 python 游戏 java
猜数字游戏代码：importrandomdefpythonit():a=random.randint(1,100)n=int(input("输入你猜想的数字："))whilen!=a:ifn>a:print("很遗憾，猜大了")n=int(input("请再次输入你猜想的数字："))elifna::如果玩家猜的数字n大于随机数字a，则输出"很遗憾，猜大了"，并提示玩家再次输入。elifn
用Python实现读取统计单词个数程序媛了了 python 游戏 java
完整实例代码：fromcollectionsimportCounterdefpythonit():danci={}withopen("pythonit.txt","r",encoding="utf-8")asf:foriinf:words=i.strip().split()forwordinwords:ifwordnotindanci:danci[word]=1else:danci[word]+=
VMware Workstation 11 或者 VMware Player 7安装MAC OS X 10.10 Yosemite iwindyforest vmware mac os 10.10 workstation player
最近尝试了下VMware下安装MacOS 系统，安装过程中发现网上可供参考的文章都是VMware Workstation 10以下， MacOS X 10.9以下的文章，只能提供大概的思路，但是实际安装起来由于版本问题，走了不少弯路，所以我尝试写以下总结，希望能给有兴趣安装OSX的人提供一点帮助。写在前面的话：其实安装好后发现，由于我的th
关于《基于模型驱动的B/S在线开发平台》源代码开源的疑虑？ deathwknight JavaScript java 框架
本人从学习Java开发到现在已有10年整，从一个要自学 java买成javascript的小菜鸟，成长为只会java和javascript语言的老菜鸟（个人邮箱：[email protected]）一路走来，跌跌撞撞。用自己的三年多业余时间，瞎搞一个小东西（基于模型驱动的B/S在线开发平台，非MVC框架、非代码生成）。希望与大家一起分享，同时有许些疑虑，希望有人可以交流下平台
如何把maven项目转成web项目 Kai_Ge maven MyEclipse
创建Web工程，使用eclipse ee创建maven web工程 1.右键项目,选择Project Facets,点击Convert to faceted from 2.更改Dynamic Web Module的Version为2.5.(3.0为Java7的,Tomcat6不支持). 如果提示错误,可能需要在Java Compiler设置Compiler compl
主管？？？ Array_06 工作
转载：http://www.blogjava.net/fastzch/archive/2010/11/25/339054.html 很久以前跟同事参加的培训，同事整理得很详细，必须得转！前段时间，公司有组织中高阶主管及其培养干部进行了为期三天的管理训练培训。三天的课程下来，虽然内容较多，因对老师三天来的课程内容深有感触，故借着整理学习心得的机会，将三天来的培训课程做了一个
python内置函数大全 2002wmj python
最近一直在看python的document，打算在基础方面重点看一下python的keyword、Build-in Function、Build-in Constants、Build-in Types、Build-in Exception这四个方面，其实在看的时候发现整个《The Python Standard Library》章节都是很不错的，其中描述了很多不错的主题。先把Build-in Fu
JSP页面通过JQUERY合并行 357029540 JavaScript jquery
在写程序的过程中我们难免会遇到在页面上合并单元行的情况，如图所示如果对于会的同学可能很简单，但是对没有思路的同学来说还是比较麻烦的，提供一下用JQUERY实现的参考代码 function mergeCell(){ var trs = $("#table tr"); &nb
Java基础冰天百华 java基础
学习函数式编程 package base; import java.text.DecimalFormat; public class Main { public static void main(String[] args) { // Integer a = 4; // Double aa = (double)a / 100000; // Decimal
unix时间戳相互转换 adminjun 转换 unix 时间戳
如何在不同编程语言中获取现在的Unix时间戳(Unix timestamp)？ Java time JavaScript Math.round(new Date().getTime()/1000) getTime()返回数值的单位是毫秒 Microsoft .NET / C# epoch = (DateTime.Now.ToUniversalTime().Ticks - 62135
作为一个合格程序员该做的事 aijuans 程序员
作为一个合格程序员每天该做的事 1、总结自己一天任务的完成情况最好的方式是写工作日志，把自己今天完成了什么事情，遇见了什么问题都记录下来，日后翻看好处多多 2、考虑自己明天应该做的主要工作把明天要做的事情列出来，并按照优先级排列，第二天应该把自己效率最高的时间分配给最重要的工作 3、考虑自己一天工作中失误的地方，并想出避免下一次再犯的方法出错不要紧，最重
由html5视频播放引发的总结 ayaoxinchao html5 视频 video
前言项目中存在视频播放的功能，前期设计是以flash播放器播放视频的。但是现在由于需要兼容苹果的设备，必须采用html5的方式来播放视频。我就出于兴趣对html5播放视频做了简单的了解，不了解不知道，水真是很深。本文所记录的知识一些浅尝辄止的知识，说起来很惭愧。视频结构本该直接介绍html5的<video>的，但鉴于本人对视频
解决httpclient访问自签名https报javax.net.ssl.SSLHandshakeException: sun.security.validat bewithme httpclient
如果你构建了一个https协议的站点，而此站点的安全证书并不是合法的第三方证书颁发机构所签发，那么你用httpclient去访问此站点会报如下错误 javax.net.ssl.SSLHandshakeException: sun.security.validator.ValidatorException: PKIX path bu
Jedis连接池的入门级使用 bijian1013 redis redis数据库 jedis
Jedis连接池操作步骤如下： a.获取Jedis实例需要从JedisPool中获取； b.用完Jedis实例需要返还给JedisPool； c.如果Jedis在使用过程中出错，则也需要还给JedisPool； packag
变与不变 bingyingao 不变变亲情永恒
变与不变周末骑车转到了五年前租住的小区，曾经最爱吃的西北面馆、江西水饺、手工拉面早已不在，各种店铺都换了好几茬，这些是变的。三年前还很流行的一款手机在今天看起来已经落后的不像样子。三年前还运行的好好的一家公司，今天也已经不复存在。一座座高楼拔地而起，
【Scala十】Scala核心四：集合框架之List bit1129 scala
Spark的RDD作为一个分布式不可变的数据集合，它提供的转换操作，很多是借鉴于Scala的集合框架提供的一些函数，因此，有必要对Scala的集合进行详细的了解 1. 泛型集合都是协变的，对于List而言，如果B是A的子类，那么List[B]也是List[A]的子类，即可以把List[B]的实例赋值给List[A]变量 2. 给变量赋值(注意val关键字，a，b
Nested Functions in C bookjovi c closure
Nested Functions 又称closure，属于functional language中的概念，一直以为C中是不支持closure的，现在看来我错了，不过C标准中是不支持的，而GCC支持。既然GCC支持了closure，那么 lexical scoping自然也支持了，同时在C中label也是可以在nested functions中自由跳转的
Java-Collections Framework学习与总结-WeakHashMap BrokenDreams Collections
总结这个类之前，首先看一下Java引用的相关知识。Java的引用分为四种：强引用、软引用、弱引用和虚引用。强引用：就是常见的代码中的引用，如Object o = new Object();存在强引用的对象不会被垃圾收集
读《研磨设计模式》-代码笔记-解释器模式-Interpret bylijinnan java 设计模式
声明：本文只为方便我个人查阅和理解，详细的分析以及源代码请移步原作者的博客http://chjavach.iteye.com/ package design.pattern; /* * 解释器（Interpreter）模式的意图是可以按照自己定义的组合规则集合来组合可执行对象 * * 代码示例实现XML里面1.读取单个元素的值 2.读取单个属性的值 * 多
After Effects操作&快捷键 cherishLC After Effects
1、快捷键官方文档中文版：https://helpx.adobe.com/cn/after-effects/using/keyboard-shortcuts-reference.html 英文版：https://helpx.adobe.com/after-effects/using/keyboard-shortcuts-reference.html 2、常用快捷键
Maven 常用命令 crabdave maven
Maven 常用命令 mvn archetype:generate mvn install mvn clean mvn clean complie mvn clean test mvn clean install mvn clean package mvn test mvn package mvn site mvn dependency:res
shell bad substitution daizj shell 脚本
#!/bin/sh /data/script/common/run_cmd.exp 192.168.13.168 "impala-shell -islave4 -q 'insert OVERWRITE table imeis.${tableName} select ${selectFields}, ds, fnv_hash(concat(cast(ds as string), im
Java SE 第二讲（原生数据类型 Primitive Data Type） dcj3sjt126com java
Java SE 第二讲： 1. Windows: notepad, editplus, ultraedit, gvim Linux: vi, vim, gedit 2. Java 中的数据类型分为两大类： 1）原生数据类型（Primitive Data Type） 2）引用类型（对象类型）（R
CGridView中实现批量删除 dcj3sjt126com PHP yii
1，CGridView中的columns添加 array( 'selectableRows' => 2, 'footer' => '<button type="button" onclick="GetCheckbox();" style=&
Java中泛型的各种使用 dyy_gusi java 泛型
Java中的泛型的使用：1.普通的泛型使用在使用类的时候后面的<>中的类型就是我们确定的类型。 public class MyClass1<T> {//此处定义的泛型是T private T var; public T getVar() { return var; } public void setVa
Web开发技术十年发展历程 gcq511120594 Web 浏览器数据挖掘
回顾web开发技术这十年发展历程： Ajax 03年的时候我上六年级，那时候网吧刚在小县城的角落萌生。传奇，大话西游第一代网游一时风靡。我抱着试一试的心态给了网吧老板两块钱想申请个号玩玩，然后接下来的一个小时我一直在，注，册，账，号。彼时网吧用的512k的带宽，注册的时候，填了一堆信息，提交，页面跳转，嘣，”您填写的信息有误，请重填”。然后跳转回注册页面，以此循环。我现在时常想，如果当时a
openSession()与getCurrentSession()区别： hetongfei java DAO Hibernate
来自 http://blog.csdn.net/dy511/article/details/6166134 1.getCurrentSession创建的session会和绑定到当前线程,而openSession不会。 2. getCurrentSession创建的线程会在事务回滚或事物提交后自动关闭,而openSession必须手动关闭。这里getCurrentSession本地事务(本地
第一章安装Nginx+Lua开发环境 jinnianshilongnian nginx lua openresty
首先我们选择使用OpenResty，其是由Nginx核心加很多第三方模块组成，其最大的亮点是默认集成了Lua开发环境，使得Nginx可以作为一个Web Server使用。借助于Nginx的事件驱动模型和非阻塞IO，可以实现高性能的Web应用程序。而且OpenResty提供了大量组件如Mysql、Redis、Memcached等等，使在Nginx上开发Web应用更方便更简单。目前在京东如实时价格、秒
HSQLDB In-Process方式访问内存数据库 liyonghui160com
HSQLDB一大特色就是能够在内存中建立数据库，当然它也能将这些内存数据库保存到文件中以便实现真正的持久化。先睹为快！下面是一个In-Process方式访问内存数据库的代码示例：下面代码需要引入hsqldb.jar包（hsqldb-2.2.8） import java.s
Java线程的5个使用技巧 pda158 java 数据结构
Java线程有哪些不太为人所知的技巧与用法？　　萝卜白菜各有所爱。像我就喜欢Java。学无止境，这也是我喜欢它的一个原因。日常工作中你所用到的工具，通常都有些你从来没有了解过的东西，比方说某个方法或者是一些有趣的用法。比如说线程。没错，就是线程。或者确切说是Thread这个类。当我们在构建高可扩展性系统的时候，通常会面临各种各样的并发编程的问题，不过我们现在所要讲的可能会略有不同。
开发资源大整合：编程语言篇——JavaScript（1） shoothao JavaScript
概述：本系列的资源整合来自于github中各个领域的大牛，来收藏你感兴趣的东西吧。程序包管理器管理javascript库并提供对这些库的快速使用与打包的服务。 Bower - 用于web的程序包管理。 component - 用于客户端的程序包管理，构建更好的web应用程序。 spm - 全新的静态的文件包管
避免使用终结函数 vahoa.ma java jvm C++
终结函数（finalizer）通常是不可预测的，常常也是很危险的，一般情况下不是必要的。使用终结函数会导致不稳定的行为、更差的性能，以及带来移植性问题。不要把终结函数当做C++中的析构函数（destructors）的对应物。我自己总结了一下这一条的综合性结论是这样的： 1）在涉及使用资源，使用完毕后要释放资源的情形下，首先要用一个显示的方