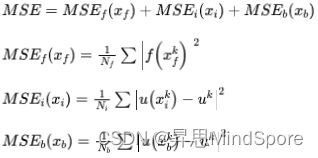技术干货 | MindSpore AI科学计算（一）：PINNS和Simnet分析

本篇是MindSpore AI科学计算系列，将主要分享美国布朗大学George Em Karniadakis教授所在课题组提出的物理信息神经网络（Physics Informed Deep Learning，PINNs），以及英伟达公司基于该算法开发的物理仿真工具包SimNet。

背景介绍

从宇宙星体的运动，到温度风速的气象预报，再到分子原子间的相互作用，很多工程学、自然科学、经济和商业过程都可以通过微分方程描述。然而微分方程如电磁领域的麦克斯韦方程（Maxwell's Equations）、流体领域的纳维-斯托克斯方程（Navier-Stokes Equations，NS）等由于其复杂性和非线性导致很难找到解析解，只能通过有线差分、有限元、有线体积等数值方法近似计算。

传统的数值方法存在网格剖分困难、计算时间长等问题。神经网络具有万能逼近能力和高效推理性能，这使得神经网络在求解微分方程时具有巨大的潜在优势。PINNs方法是一类结合物理信息约束的微分方程AI求解方法，下面将重点展开介绍。

PINNs算法介绍

考虑如下Burgers方程：

速度u是待求的物理量，t和x分别表示时间和空间坐标。上述三个等式分别表示方程、初始条件和边界条件。传统的数值方法会通过有限差分等近似表示方程中的微分，既而迭代求解获得速度u。PINNs方法则利用神经网络来表征速度u，再通过上述三个等式获得损失函数，其中下标f、i、b分别代表方程、初始条件和边界条件：

经过神经网络的反向传播，更新网络的权重，最终获得所需要的解。PINNs的核心是将方程求解转化成了优化问题，思想朴素较容易理解。相比传统方法，其优势在于无需网格剖分，取代的是数据采样，另外由于是AI方法，可以很方便地计算反问题。相比纯数据驱动的AI方法，其优势在于可以避免数据生成带来的成本和网格独立性等问题。
PINNs方法也有其不足的地方，因为缺乏严格的理论证明，很难保证能够获得很好的结果，针对介质/分辨率变化的场景，网络都需要重新训练，端到端性能相比经典方法优势不是很大；此外神经网络也引入了大量的超参，包括网络结构、学习率、激活函数等，这给求解带来了困难。

SimNet工具包介绍

SimNet应用场景

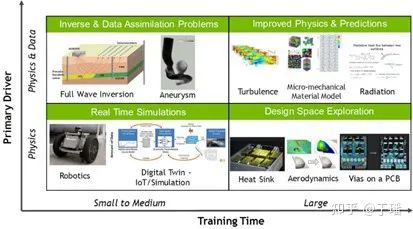
SimNet是Nvidia公司开发的基于PINNs方法的多物理场AI仿真工具包，可用来解决正向、逆向以及数据同化等问题。业界还有类似的工具包如Tensorflow版本的DeepXDE，Keras版本的SCiANN，以及Julia版本的NeuralPDE.jl等。SimNet号称可以解决复杂3D问题，下图1是SimNet可以解决的四大主力场景：

图1 SimNet四大主力场景

（1）逆向模拟/数据同化：通过拟合观测数据确定体系的物理性质，例如借助声波数据反推地层速度模型，进而计算该区域内油气含量；又如利用颅内动脉瘤的CT或者核磁共振图像数据，逆向计算不同物理量如速度、压力等。

（2）改善低精度物理模型精度：使用高精度物理模型结果或实验数据训练AI模型，再修正低精度物理模型参数，从而提升后者的准确率，可用于湍流、微机械材料模型以及辐射等问题。例如可以用直接数值模拟（DNS）的数据训练AI模型，修正RANS中的粘性等参数。

（3）实时仿真：神经网络模型的推理耗时相比传统方法少，因此可以用于对仿真的实时性要求较高的场景，例如机器人控制，数字孪生物联网或仿真等。

（4）产品设计和优化：PINNs方法可以将几何结构参数化，一次训练学习不同参数产品的特性，加速产品设计和优化，可用于散热器、空气动力学装置以及PCB板等。

SimNet框架

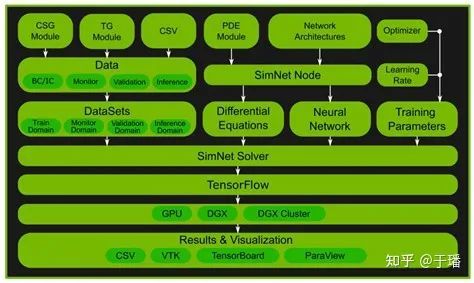
SimNet框架如图2所示，主要由前端输入、求解器、深度学习框架、数据保存和可视化组成。前端输入包括几何结构的定义及数据采样，微分方程、神经网络架构以及优化器、学习率等训练参数的设置。求解器涵盖PINNs算法以及整个训练、推理流程。深度学习框架是谷歌的Tensorflow，支持的硬件有GPU、DGX以及DGX Cluster。保存的数据格式是CSV和VTK，可视化的工具为TensorBoard和ParaView。为了提升模型的精度，SimNet采用了有符号距离场 （Signed Distance Field, SDF） 来表征数据点到边界的距离，用以调节边界和内部点损失函数的权重，避免边界跳变对结果的影响。为了能够加速复杂结构的SDF生成，英伟达开发了OptiX自定义库。

图2 SimNet框架图

相关案例

下面以二维顶盖驱动流（Lid Driven Cavity Flow，LDC）为例介绍SimNet使用。

图3 顶盖驱动流示意图

LDC的几何结构如图3，方腔内的流体初始时刻静止，顶部流体以1m∕s的速度沿x方向拖动。其余边界是固体表面，壁面的高度为0.1m，雷诺数设为10。SimNet LDC的代码主要包含几何结构构建，方程、初边界条件定义，以及神经网络构建和求解，代码如下：

几何结构构建：

height = 0.1
width = 0.1
vel = 1.0
rec = Rectangle((-width / 2, -height / 2), (width / 2, height / 2))
geo = rec

训练数据：

class LDCTrain(TrainDomain):
 def __init__(self, **config):
 super(LDCTrain, self).__init__()
 #顶部采样
 topWall = geo.boundary_bc(outvar_sympy={'u': vel, 'v': 0}, batch_size_per_area=10000, 
 lambda_sympy={'lambda_u': 1.0 - 20 * Abs(x), # weight edges to be zero
 'lambda_v': 1.0},
 criteria=Eq(y, height / 2))
 self.add(topWall, name="TopWall")
 
 # 内部采样
 interior = geo.interior_bc(outvar_sympy={'continuity': 0, 'momentum_x': 0, 'momentum_y': 0},
 bounds={x: (-width / 2, width / 2),
 y: (-height / 2, height / 2)},
 lambda_sympy={'lambda_continuity': geo.sdf,
 'lambda_momentum_x': geo.sdf,
 'lambda_momentum_y': geo.sdf},
 batch_size_per_area=400000)
 self.add(interior, name="Interior")

验证数据：

mapping = {'Points:0': 'x', 'Points:1': 'y', 'U:0': 'u', 'U:1': 'v', 'p': 'p'}
openfoam_var = csv_to_dict('openfoam/cavity_uniformVel0.csv', mapping)
openfoam_var['x'] += -width / 2 # center OpenFoam data
openfoam_var['y'] += -height / 2 # center OpenFoam data
openfoam_invar_numpy = {key: value for key, value in openfoam_var.items() if key in ['x', 'y']}
openfoam_outvar_numpy = {key: value for key, value in openfoam_var.items() if key in ['u', 'v']}
class LDCVal(ValidationDomain):
 def __init__(self, **config):
 super(LDCVal, self).__init__()
 val = Validation.from_numpy(openfoam_invar_numpy, openfoam_outvar_numpy)
 self.add(val, name='Val')

模型构建及训练：

class LDCSolver(Solver):
 train_domain = LDCTrain
 val_domain = LDCVal
 def __init__(self, **config):
 super(LDCSolver, self).__init__(**config)
 self.equations = NavierStokes(nu=0.01, rho=1.0, dim=2,
 time=False).make_node()
 flow_net = self.arch.make_node(name='flow_net',
 inputs=['x', 'y'],
  outputs=['u', 'v', 'p'])
 self.nets = [flow_net]

MindSpore官方资料

官方QQ群 : 486831414

官网：https://www.mindspore.cn/

Gitee : https : //gitee.com/mindspore/mindspore

GitHub : https://github.com/mindspore-ai/mindspore

论坛：https://bbs.huaweicloud.com/forum/forum-1076-1.html