机器学习之评价指标（accuracy,precision,recall等）

1.模型评价指标

                             | 真实类别|
		                     | 1  |  0 |
	预测类别     	|positive|-TP-| FP |
		            |negative| FN | FN |

准确度（accuracy）:全部预测正确（包括正样本和负样本）的样本占所有样本的比例。

精确度（precision）：预测值为1且真实值也为1的样本在预测值为1的样本中所占的比例，即预测为1结果的结果中有多少预测正确。

召回率（recall）:预测值为1且真实值也为1的样本在真实值为1的所有样本中所占的比例，即样本值为1 的样本有多少被检测出来。

F1：
F1分数（F1 Score）是统计学中用来衡量分类模型精确度的一种指标。它同时兼顾了分类模型的准确率和召回率。F1分数可以看作是模型准确率和召回率的一种加权平均，它的最大值是1，最小值是0，F1分数越接近1，即认为模型效果越好。F1的公式如下所示:

2. ROC曲线，AUC值

ROC曲线

接收者操作特征曲线（receiver operating characteristic curve），是反映敏感性和特异性连续变量的综合指标，ROC曲线上每个点反映着对同一信号刺激的感受性。下图是ROC曲线例子。

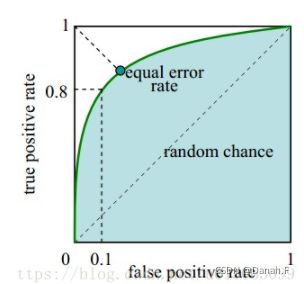
横坐标：1-Specificity，伪正类率(False positive rate，FPR，FPR=FP/(FP+TN))，预测为正但实际为负的样本占所有负例样本的比例；

纵坐标：Sensitivity，真正类率(True positive rate，TPR，TPR=TP/(TP+FN))，预测为正且实际为正的样本占所有正例样本的比例。

真正的理想情况，TPR应接近1，FPR接近0，即图中的（0,1）点。ROC曲线越靠拢（0,1）点，越偏离45度对角线越好。

AUC值

AUC (Area Under Curve) 被定义为ROC曲线下的面积，显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围一般在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好，而作为一个数值，对应AUC更大的分类器效果更好。

从AUC判断分类器（预测模型）优劣的标准：

AUC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器。
0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

3. P-R曲线、AP、mAP

Precision x Recall曲线（PR曲线）

通过改变置信度confidence的值，可以针对每一个类别画出一条precision-recall曲线。通过设置不同的confidence，可以得到不同的precision和recall的对应关系。

观察某一个目标检测模型关于某一类别的PR曲线，如果随着recall的增高，其precision仍旧保持较高的值（无论如何设置confidence的阈值，precision和recall都能保持较高的值），那么我们就可以认为对于该类别来说，该模型具有比较好的性能。

判断目标检测模型性能好坏的另外一种方式是：看该模型是否只会识别出真实的目标（False Positives的个数为0，即高precision），同时能够检测出所有的真实目标（False Negatives的个数为0，即高recall）。

而一个性能比较差的模型要想检测出所有的真实目标（高recall），就需要增加其检测出的目标的个数（提高False Positive），这会导致模型的precision降低。在实际测试中，我们会发现PR曲线在一开始就有较高的precision，但随着recall的增高，precision会逐渐降低。

Average Precision

另外一种表征目标检测模型性能的方式是计算PR曲线下的面积（area under the curve, AUC）。因为PR曲线总是呈Z字型上升和下降，因而我们很难将多个模型的PR曲线绘制在一起进行比较（曲线会相互交叉）。这也是我们常使用AP这一具有具体的数值的度量方式的原因。

实际上，可以将AP看作precision以recall为权重的加权平均。

3.目标检测常用指标

要了解目标检测的性能，首先了解检测框预测正确的标准。主要有两个阈值：IoU阈值和置信度（confidence）阈值。
置信度即模型认为检测框中存在目标的置信度。对于一个检测框，只有当其置信度大于该阈值时才认为检测狂中存在目标。
IoU就是交并比，即两个矩形框重合部分的面积占两个矩形框面积之和的比例。当模型给出的检测框和真实的目标框之间的IoU大于该阈值时，才认为该检测框是正确的。

4. COCO评价标准

准确率、精确率、召回率、F1值、ROC/AUC整理笔记

参考链接：https://blog.csdn.net/qq_38947129/article/details/100920962
https://blog.csdn.net/weixin_42118657/article/details/112250953