PyTorch踩坑指南（2）损失函数nn.NLLLoss()和nn.CrossEntropyLoss()

前言

深度学习模型优化，即优化网络权值使得该模型拟合数据的能力达到最优，而最优的一个标准是损失函数较小（兼顾训练数据和测试数据，以及实际应用场景的最优）。PyTorch中有很多损失函数，这里我主要介绍最常用的两种，NLLLoss和CrossEntropyLoss；而实际上CrossEntropyLoss更常用，NLLLoss与其的关系也会在本文中详细介绍。

1. Softmax

要介绍上述两个损失函数的关系，得先从Softmax说起。Softmax函数是一个非线性转换函数，通常用在网络输出的最后一层，Softmax处理之后的输出的是归一化的概率分布，即各个类别的概率值在$[0,1]$之间且概率和为1）¹。如在多分类问题中，Softmax输出每个类别或节点对应的概率。其计算公式如下，$$\sigma (z{)}_i=\frac{e^{z_i}}{{\sum }_{j=1}^K{e}^{z_j}}$$其中，$z$是输入向量（神经网络output layer的输出向量），$z_i$为输入向量第$i$个节点的值，如下图所示。

对output layer的值可以直接做Logsoftmax操作，该操作之后的值作为NLLLoss的输入。

2. NLLLoss

NLLLoss的全称为Negative Log Likelihood Loss，负对数似然损失，是训练多分类问题的常用损失函数²。Likelihood想必大家都熟悉，是似然的意思，而最大似然估计（MLE，maximum likelihood estimation）是一种估计模型参数的方法。NLLLoss，刨去Negative和Log，因为这两个是取负数和取对数的数学操作，剩下的Likelihood Loss，就是这个损失函数的本质了。于是引申出一个问题——似然函数为什么可以作为模型的损失函数（这个问题大部分博文都没有详细讲，我来给大家抛砖引玉，如有理解不对的地方，请大伙儿批评指正）。

2.1 似然函数

似然（函数）这一概念是由Fisher提出。当我们有一系列观测数据$x$，我们使用该观测数据进行模型参数$\theta$估计，就用到了似然函数，$L(\theta |x)$

这里插一个对概率的解释。$L(\theta |x)=f(x|\theta )$ ，左边表示likelihood，右边表示probability—— It can be called the likelihood of θ (given that x was observed) or the probability of x (given θ) ³——这个等式表示的是对于同一件事件发生的两种思考角度，核心意思为给定一个$\theta$和观测数据$x$的情况下，整个事件发生的可能性。

统计学观点认为样本的出现是基于一个分布。那么我们先假设这个分布为$f$，参数为$\theta$。不同的$\theta$，样本分布不一样，即出现$x$的概率也不一样。$L(\theta |x)$ 表示的是在给定样本$x$的时候，参数$\theta$使得$x$出现的可能性多大。

所以，似然函数实际上表示的是参数$\theta$的函数，而最大似然估计的意思是寻找一个$\theta$使得该函数值最大。我们拿抛硬币举例，正面向上的概率为$\theta$，反面向上的概率为$1-\theta$。假如我们抛$N$次，其中$N_1$次正面朝上，$N_2$次反面朝上，那么$$L(\theta |x)={\theta }^{N_1}(1-\theta {)}^{N_2}$$
可以基于此表达式画出$L$的函数曲线。

import matplotlib.pyplot as plt
import numpy as np

N = 100
N1 = 60
N2 = N - N1

theta = np.arange(0.10, 0.90, 0.05)
L = np.zeros(theta.size)

for i in range(theta.size):
    L[i] =  np.power(theta[i], N1) * np.power(1-theta[i], N2)

# find the theta makes the L funtion maximum
value = np.max(L)
ind = np.where(L==value)
# draw the Likelihood function
plt.figure()
plt.plot(theta, L)
plt.text(theta[ind],value,(theta[ind],value),color='r')
plt.show()

可以看出，当100次抛硬币，60次正面朝上的情况下，$\theta$的最大似然估计值为$0.6$

2.2 似然损失

损失函数用于衡量当前参数（神经网络模型中的weights和biases；高斯混合模型中的均值，方差，权重）下，模型的预测值和真实值（label或数据观测值）的差距。所以，我们希望损失函数越小越好。

(1) 从损失函数设计直接解释

我们规定，损失函数为²$$l(x,y)=L=l_1,...,l_N,l_n=-w_{y_n}{x}_{n,y_n}$$
对于个数为$N$的batch数据，每个$x$的大小为$N\ast C$，$C$为类别数，且$x$为——神经网络的output layer，经过LogSoftmax之后的值；而$x_n$为该batch中，第$n$个向量；$y_n$表示该batch中，第$n$个向量的label或者target。我们取向量$x_n$中，第target位置的值，然后乘以权重（如果有，一般情况下为$1$），取负号，可得第$n$个数据的损失。该batch的综合损失为²，$$l(x,y)=\{\begin{array}{rlrl}& \sum _{n=1}^N\frac{1}{{\sum }_{n=1}^N{w}_{y_n}}{l}_n,& ifreduction& {=}^{\prime }mea{n}^{\prime }\\ & \sum _{n=1}^N{l}_n,& ifreduction& {=}^{\prime }su{m}^{\prime }\end{array}$$
很显然，一个是求和，一个是求平均。
当预测值越接近真值（label或者target）的时候，也就是说概率值在target这个位置越大，说明这个模型就越准确。概率$P(x)$的值为$[0,1]$（softmax操作），取对数后为$(-\infty ,0]$(Logsoftmax操作)，在前面加个符号，变成$[0,\infty )$，为损失函数的取值范围。换句话说，概率越接近$1$，损失函数越小，越接近零。符合我们优化的目标，如下图所示⁴。

更直观一点，如下图所示⁴，“马” 的预测概率值为$0.98$，非常高，其对应的NLLLoss为$0.02$，很小。

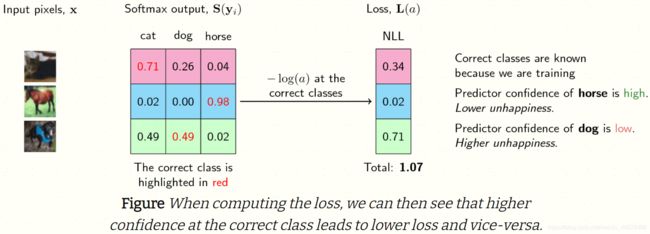
(2) 从多项分布理解损失函数设计

前文中提到似然函数的时候用抛硬币举例子，而多次抛硬币实际上是一个二项分布⁵，单次实验为伯努利实验，$n$为抛硬币次数，$k$为正面朝上的次数，$p$为正面朝上的概率，其概率质量函数为$$f(k,n,p)=Pr(X=k)=\left(\begin{array}{c}n\\ k\end{array}\right)p^k(1-p{)}^{n-k}$$
而多项分布可以理解为掷色子，其概率质量函数为，
$$\begin{array}{rl}f(x_1,...,x_k;n,p1,...,pk)& =Pr(X1=x_1,X_2=x_2,...,X_k=x_k)\\ & =\frac{n!}{x_1!...x_k!}{p}_1^{x_1}\times ...\times p_k^{x_k}\end{array}$$
对于每次模型的输出概率，即label的分布（如$k$个类别），可以理解为多项式分布。更直观一点，输入同一张图片——还是以上图中的“马”为例子——100次，它的被模型预测到正确label的次数为98次，概率为$0.98$，模型预测输出，统计下来为$p=[0.02,0.00,0.98]$。而这张图的label，实际上就是我们“要求”模型预测出现的次数100次，则$x=[0,0,1]$。接下来，我们就有了$$f(p,x)=0.02^0\times 0.00^0\times 0.98^1$$最大化似然函数，可知，$p=x$的时候，得到最大值1。log不改变单调性，也可使得上述乘法变成加法$$log(f(p,x))=\sum x\times log(p)$$最大化似然，进一步就变成了最小化负的log似然$$loss(p,x)=-\sum x\times log(p)$$如此看来，负log似然损失可以作为模型训练的损失函数——模型输入的预测概率越接近label，loss越小，接近零。

3. CrossEntropyLoss

看完负log似然损失函数，我们会发现，这个跟交叉熵形式一样啊，没错，实际上就是相通的。同一个事物的不同解释角度，殊途同归。

3.1 交叉熵

实在是懒得敲公式了，直接贴官网的图⁶——吐槽一下CSDN的latex接口实在是不太友好。实际上，pytorch的这个计算公式里面，log里面就是一个softmax，然后加上一个NLLLoss。对于标签来讲，除了$0$就是$1$，就变成了下面这个形式，标签为$1$，就是乘以$1$，在公式形式上也省了，也就是后面说的P(X)省了——样本真实分布，只剩下Q(X)——模型预测输出。

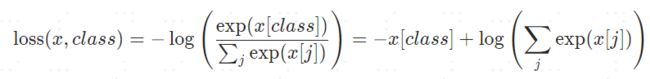
交叉熵从字面意思理解就是交叉+熵。熵，是信息函数关于概率分布P的期望，这个期望值就是熵，公式如下$$H(X)=-\sum _i^{n}P(X=x_i)log(P(X=x_i))$$那cross就是真实分布$p$和模型预测$q$进行cross了$$H(p,q)=-\sum _i^{n}p(x_i)log(\mathbf{q}({\mathbf{x}}_{\mathbf{i}}))$$

3.2 KL散度⁷

如果对于同一个随机变量$X$有两个单独的概率分布$P(x)$和$Q(x)$，则我们可使用KL算的来衡量这两个概率分布的差异。$$D_{KL}(p||q)=\sum _{i=1}^{n}p(x_i)log(\frac{p(x_i)}{q(x_i)})$$深度学习中，$P(x)$样本真实分布，$Q(x)$表示模型预测输出，还拿上面的猫，狗，马分类为例，第二张马的照片，真实分布$P(X)=[0,0,1]$，预测分布$Q(X)=[0.02,0.00,0.98]$，计算KL散度$$\begin{array}{rl}{D}_{KL}(p||q)& =\sum _{i=1}^{n}p(x_i)log(\frac{p(x_i)}{q(x_i)})\\ & =p(x_1)log\left(\frac{p(x_1)}{q(x_1)}\right)+p(x_2)log\left(\frac{p(x_2)}{q(x_2)}\right)+p(x_3)log\left(\frac{p(x_3)}{q(x_3)}\right)\\ & =1\times log\left(\frac{1}{0.98}\right)\\ & =0.0088\end{array}$$
KL散度越小，表示两个分布越接近。为啥要讲这个KL散度，因为KL散度可以拆成交叉熵和信息熵，而信息熵实际是个常量（lable是固定的）。交叉熵就是个简化的KL散度呀。我们实际上就是用的KL散度——简化成交叉熵——来训练的神经网络，让输出的分布接近真实分布（标签）。我来拆给大家看$$\begin{array}{rl}{D}_{KL}(p||q)& =\sum _{i=1}^{n}p(x_i)log(\frac{p(x_i)}{q(x_i)})\\ & =\sum _i^{n}p(x_i)log(p(x_i))-\sum _i^{n}p(x_i)log(q(x_i))\\ & =-H(p(x))+[-\sum _i^{n}p(x_i)log(q(x_i)\left)\right]\end{array}$$
结论就是KL散度 = 交叉熵 -（信息）熵

Show me the codes

前文我们说到，pytorch中的CrossEntroyLoss是LogSoftmax + NLLLoss。我们用代码验证一下

import torch.nn as nn
import torch
import math

def softmax_(input_x):
    x_exp = [math.exp(i) for i in input_x]
    sum_x_exp = sum(x_exp)
    # softmax_result = [round(i / sum_x_exp, 4) for i in x_exp]
    softmax_result = [(i / sum_x_exp) for i in x_exp]
    # convert to tensor
    softmax_result = torch.tensor(softmax_result, dtype = torch.float)
    return softmax_result
    
def log_softmax_(input_x):
    softmax_value = softmax_(input_x)
    log_softmax_result = [math.log(i) for i in softmax_value]
    # convert to tensor
    log_softmax_result = torch.tensor(log_softmax_result, dtype = torch.float)
    return log_softmax_result

def NLLLoss_(input_x, target):
    # NLLLoss needs target and its log likelihood values
    # target is the label (or index) of input_x, choose that value
    return -input_x[0][target]

def printHead(Head):
    print('=================================================')
    print('=================='+Head)
    print('=================================================')
    
if __name__=="__main__":

    input_x = list(range(1,4))
    input_x_tensor = torch.reshape(torch.tensor(input_x, dtype = torch.float),(1,len(input_x)))
    
    # softmax by define
    output_x = softmax_(input_x)
    
    # softmax in torch
    softmax_torch = nn.Softmax(dim=1)
    output_x_tensor = softmax_torch(input_x_tensor)
    printHead('Result of softmax compare: ')
    print('mine: ', output_x)
    print('pytorch: ', output_x_tensor)
    print('\n')
    # log softmax by define
    output_x = log_softmax_(input_x)
    
    # log softmax in torch
    logsoftmax_torch = nn.LogSoftmax(dim = 1)
    output_x_tensor = logsoftmax_torch(input_x_tensor)
    printHead('Result of logsoftmax compare: ')
    print('mine: ', output_x)
    print('pytorch: ', output_x_tensor)
    print('\n')
    
    # NLLLoss by define
    target =  torch.empty(1, dtype=torch.long).random_(len(input_x))
    # print(target, len(output_x_tensor))
    NLLLoss_value = NLLLoss_(output_x_tensor, target)
    
    # NLLLoss by torch
    loss = nn.NLLLoss()
    output  = loss(output_x_tensor, target)
    printHead('Result of NLLLoss compare: ')
    print('mine NLLLoss: ', NLLLoss_value)
    print('pytorch NLLLoss: ', output)
    
    # crossentropy
    m3 = nn.CrossEntropyLoss()
    o3 = m3(input_x_tensor, target)
    print('CrossEntropyLoss Result: ', o3)
    
    ''' minibatch input 
    N = 2
    C = 3

    input = torch.randn(2,3) # N*C
    target = torch.empty(N, dtype=torch.long).random_(C)
    
    o3 = m3(input, target)
    '''

Reference

---

1. 官方文档 SOFTMAX ↩︎

2. 官方文档 NLLLoss ↩︎ ↩︎ ↩︎

3. What is the difference between probability and likelihood, Jason Eisner ↩︎

4. Understanding softmax and the negative log-likelihood,LJ MIRANDA, 2017 ↩︎ ↩︎

5. 二项分布Wiki ↩︎

6. 官方文档 CrossEntropyLoss ↩︎

7. 相对熵 ↩︎