sklearn学习谱聚类

原文链接

1. sklearn谱聚类概述

\qquad 在sklearn的类库中，sklearn.cluster.SpectralClustering实现了基于Ncut的谱聚类，没有实现基于RatioCut的切图聚类。同时，对于相似矩阵的建立，也只是实现了基于K邻近法和全连接法的方式，没有基于$ϵ$-邻近法的相似矩阵。最后一步的聚类方法则提供了两种，K-Means算法和 discretize算法。

\qquad 对于SpectralClustering的参数，我们主要需要调参的是相似矩阵建立相关的参数和聚类类别数目，它对聚类的结果有很大的影响。当然其他的一些参数也需要理解，在必要时需要修改默认参数。

2. SpectralClustering重要参数与调参注意事项

\qquad 下面我们就对SpectralClustering的重要参数做一个介绍，对于调参的注意事项会一起介绍。
\qquad 1）n_clusters：代表我们在对谱聚类切图时降维到的维数,同时也是最后一步聚类算法聚类到的维数。也就是说sklearn中的谱聚类对这两个参数统一到了一起。简化了调参的参数个数。虽然这个值是可选的，但是一般还是推荐调参选择最优参数。

\qquad 2) affinity: 也就是我们的相似矩阵的建立方式。可以选择的方式有三类，第一类是 ‘nearest_neighbors’即K邻近法。第二类是’precomputed’即自定义相似矩阵。选择自定义相似矩阵时，需要自己调用set_params来自己设置相似矩阵。第三类是全连接法，可以使用各种核函数来定义相似矩阵，还可以自定义核函数。最常用的是内置高斯核函数’rbf’。其他比较流行的核函数有‘linear’即线性核函数, ‘poly’即多项式核函数, ‘sigmoid’即sigmoid核函数。如果选择了这些核函数， 对应的核函数参数在后面有单独的参数需要调。自定义核函数我没有使用过，这里就不多讲了。affinity默认是高斯核’rbf’。一般来说，相似矩阵推荐使用默认的高斯核函数。

\qquad 3) 核函数参数gamma: 如果我们在affinity参数使用了多项式核函数 ‘poly’，高斯核函数‘rbf’, 或者’sigmoid’核函数，那么我们就需要对这个参数进行调参。

\qquad 多项式核函数中这个参数对应$K(x,z)=(\gamma x\cdot z+r{)}^d$中的$\gamma$，一般需要通过交叉验证选择一组合适的$\gamma ,r,d$
\qquad 高斯核函数中这个参数对应$K(x,z)=exp(\gamma ||x-z|{|}^2)$中的$\gamma$，一般需要通过交叉验证选择合适的$\gamma$
\qquad sigmoid核函数中这个参数对应$K(x,z)=tanh(\gamma x\cdot z+r)$中的$\gamma$，一般需要通过交叉验证选择一组合适的$\gamma ,r$
$\gamma$默认值为1.0，如果我们affinity使用’nearest_neighbors’或者是’precomputed’，则这么参数无意义。

\qquad 4）核函数参数degree：如果我们在affinity参数使用了多项式核函数 ‘poly’，那么我们就需要对这个参数进行调参。这个参数对应$K(x,z)=(\gamma x\cdot z+r{)}^d$中的d，默认是3。一般需要通过交叉验证选择一组合适的$\gamma ,r,d$

\qquad 5）核函数参数coef0: 如果我们在affinity参数使用了多项式核函数 ‘poly’，或者sigmoid核函数，那么我们就需要对这个参数进行调参。

\qquad 多项式核函数中这个参数对应$K(x,z)=(\gamma x\cdot z+r{)}^d$中的$r$。一般需要通过交叉验证选择一组合适的$\gamma ,r,d$
\qquad sigmoid核函数中这个参数对应$K(x,z)=tanh(\gamma x\cdot z+r)$中的$r$，一般需要通过交叉验证选择一组合适的$\gamma ,r$
\qquad coef0默认为1.

\qquad 6）kernel_params：如果affinity参数使用了自定义的核函数，则需要通过这个参数传入核函数的参数。

\qquad 7 ) n_neighbors: 如果我们affinity参数指定为’nearest_neighbors’即K邻近法，则我们可以通过这个参数指定KNN算法的K的个数。默认是10.我们需要根据样本的分布对这个参数进行调参。如果我们affinity不使用’nearest_neighbors’，则无需理会这个参数。

\qquad 8）eigen_solver:在降维计算特征值特征向量的时候，使用的工具。有 None, ‘arpack’, ‘lobpcg’, 和‘amg’4种选择。如果我们的样本数不是特别大，无需理会这个参数，使用’'None暴力矩阵特征分解即可,如果样本量太大，则需要使用后面的一些矩阵工具来加速矩阵特征分解。它对算法的聚类效果无影响。

\qquad 9）eigen_tol：如果eigen_solver使用了arpack’，则需要通过eigen_tol指定矩阵分解停止条件。

\qquad 10）assign_labels：即最后的聚类方法的选择，有K-Means算法和 discretize算法两种算法可以选择。一般来说，默认的K-Means算法聚类效果更好。但是由于K-Means算法结果受初始值选择的影响，可能每次都不同，如果我们需要算法结果可以重现，则可以使用discretize。

\qquad 11）n_init：即使用K-Means时用不同的初始值组合跑K-Means聚类的次数，这个和K-Means类里面n_init的意义完全相同，默认是10，一般使用默认值就可以。如果你的n_clusters值较大，则可以适当增大这个值。

\qquad 从上面的介绍可以看出，需要调参的部分除了最后的类别数n_clusters，主要是相似矩阵affinity的选择，以及对应的相似矩阵参数。当我选定一个相似矩阵构建方法后，调参的过程就是对应的参数交叉选择的过程。对于K邻近法，需要对n_neighbors进行调参，对于全连接法里面最常用的高斯核函数rbf，则需要对gamma进行调参。

3.SpectralClustering实例

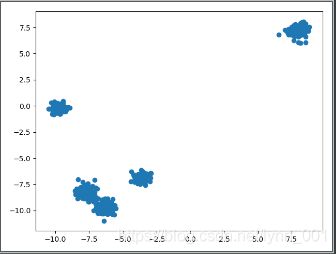
\qquad 首先我们生成500个个6维的数据集，分为5个簇。由于是6维，这里就不可视化了，代码如下:

import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

X, y = make_blobs(n_samples=500, n_features=6, centers=5, cluster_std=[0.4, 0.3, 0.4, 0.3, 0.4], random_state=11)
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.show()

\qquad 接着我们看看默认的谱聚类的效果：

y_pred = SpectralClustering().fit_predict(X)
# Calinski-Harabasz Score 14907.099436228204
print("Calinski-Harabasz Score", metrics.calinski_harabaz_score(X, y_pred))

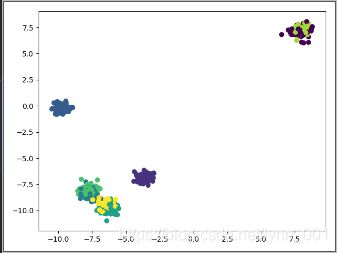
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()

\qquad 由于我们使用的是高斯核，那么我们一般需要对n_clusters和gamma进行调参。选择合适的参数值。代码如下:

for i, gamma in enumerate((0.01, 0.1, 1, 10)):
    for j, k in enumerate((3, 4, 5, 6)):
        y_pred = SpectralClustering(n_clusters=k, gamma=gamma).fit_predict(X)
        print("Calinski-Harabasz Score with gamma=", gamma, "n_clusters=", k, "score:",
              metrics.calinski_harabaz_score(X, y_pred))
              
"""
Calinski-Harabasz Score with gamma= 0.01 n_clusters= 3 score: 1979.7709609161868
Calinski-Harabasz Score with gamma= 0.01 n_clusters= 4 score: 3154.0184121901602
Calinski-Harabasz Score with gamma= 0.01 n_clusters= 5 score: 23410.63894999139
Calinski-Harabasz Score with gamma= 0.01 n_clusters= 6 score: 19303.734087657893
Calinski-Harabasz Score with gamma= 0.1 n_clusters= 3 score: 1979.7709609161868
Calinski-Harabasz Score with gamma= 0.1 n_clusters= 4 score: 3154.0184121901607
Calinski-Harabasz Score with gamma= 0.1 n_clusters= 5 score: 23410.638949991386
Calinski-Harabasz Score with gamma= 0.1 n_clusters= 6 score: 19427.96189435911
Calinski-Harabasz Score with gamma= 1 n_clusters= 3 score: 450.692778360567
Calinski-Harabasz Score with gamma= 1 n_clusters= 4 score: 120.1243266675767
Calinski-Harabasz Score with gamma= 1 n_clusters= 5 score: 23410.638949991386
Calinski-Harabasz Score with gamma= 1 n_clusters= 6 score: 633.021945343848
Calinski-Harabasz Score with gamma= 10 n_clusters= 3 score: 42.777268645847606
Calinski-Harabasz Score with gamma= 10 n_clusters= 4 score: 42.40099368087282
Calinski-Harabasz Score with gamma= 10 n_clusters= 5 score: 30.558274478353223
Calinski-Harabasz Score with gamma= 10 n_clusters= 6 score: 47.37991118563843
"""

\qquad 可见最好的n_clusters是5，而最好的高斯核参数是1或者0.1，或者0.01。

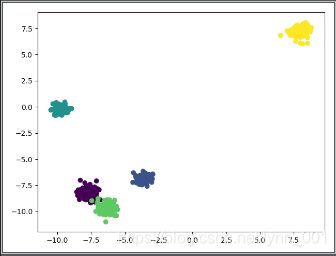
\qquad 将n_clusters=5，gamma=0.1可视化

y_pred = SpectralClustering(n_clusters=5, gamma=0.1).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()