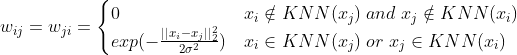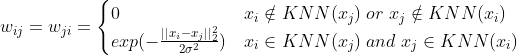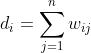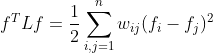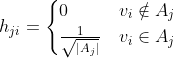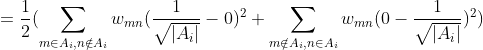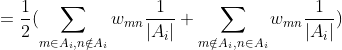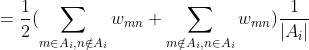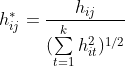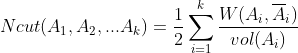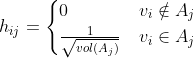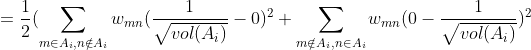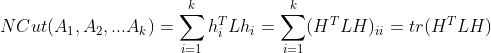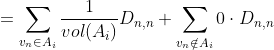机器学习笔记（十二）谱聚类原理和实践

本文我们继续介绍聚类家族中的另一个成员——谱聚类（Spectral clustering）。谱聚类最早来源于图论，后来由于性能优异，被广泛应用于聚类中。相比K-Means等聚类算法，谱聚类对数据分布的适应性更强（如kmeans要求数据为凸集，谱聚类对数据结构并没有太多的假设要求），聚类效果也很优秀，同时聚类的计算量也小很多（意味着更快的速度），也无需像GMM一样对数据的概率分布做假设，更加难能可贵的是实现起来也不复杂。因此，如果有一个需要尝试聚类解决的问题，那么谱聚类一定是你的优先选择之一。当然，每一种算法有自己的优点，也有自己的缺点，谱聚类也不例外，下文中我们会详细介绍谱聚类的原理。

一、原理

1.1 算法背景

在介绍具体的算法原理之前，我们不妨回想一下聚类的本质或者说目的是什么，简单地说就是：让距离更近（相似）的样本聚集到一起，距离较远（相异）的样本分属到不同的簇中。整个数据集我们可以认为是一个任意两个点之间都有连线的加权无向图，其中权重就是两个点之间的距离函数（这里我们一般取距离的递减函数，即距离越大，权重越小，距离越小，权重越大，表示越紧密），当然这里的距离可以自定义，如欧氏距离、余弦距离等，也可以设置一个阈值，大于这个阈值的认为是无穷大，小于的都设置为一个定值。聚类的结果就好像现在我们要把整个数据集切开，切成需要的份数，最终的结果就是每个子集里面的样本权重尽可能大，子集之间被切断的权重尽可能小，现在问题就是：我们应该怎么切才可以更加高效的得到更好的结果呢？这也就是Spectral clustering要解决的问题。因此，Spectral clustering算法可以分为两步：第一，基于已有的数据集构图；第二，基于第一步的图切图。下面我们分别介绍这两个步骤。

1.2 谱聚类构图

对于一个加权重无向图 G(V, E)，V显然就是我们数据集中的所有样本点，因此，我们需要确定的主要就是边 E，更确切的说是 E 的权重。所有样本点边权重组成的矩阵，又称之为邻接矩阵 W。构建邻接矩阵 W 的方法主要有三类：ϵ-邻近法，K邻近法和全连接法。

1. ϵ-邻近法

ϵ-邻近法的计算比较简单，它设置了一个距离阈值ϵ，然后用任意两个样本点之间的欧氏距离  和 ϵ 的大小关系来定量样本之间的边权重。计算如下：

                                                 

可以发现，ϵ-邻近法构建的邻接矩阵权重值只有 0 和 ϵ 的稀疏矩阵，优点是计算简单，适合大样本的项目，缺点是距离远近度量很不精确，信息丢失严重，结果依赖 ϵ 的选择。因此在实际应用中，我们很少使用ϵ-邻近法。

2. K 邻近法

K 邻近法利用 KNN 算法遍历所有的样本点，取每个样本最近的 k 个点作为近邻，但是这种方法会造成重构之后的邻接矩阵 W 非对称，因为 A是B的 k 近邻点，但是B未必是A的k近邻点。为什么要求邻接矩阵一定要对称呢？我们下文会再介绍。为了解决不对称问题，有两种处理方法：

第一种，只要一个样本点是其他样本点的k近邻点，则就保留这两个点之间的距离值，换句话说就是权重值，即权重值为：

                                                 

第二种，只有两个样本点之间互为k近邻点的时候，才保留权重值，即权重值为：

                                                 

3. 全连接法

全连接法，顾名思义就是保留所有样本点之间的权重值，计算方法如下;

                                                 

这里我们计算权重的距离函数采用高斯核计算，当然也可以采用多项式核函数、sigmoid核函数等常用核函数，一般高斯径向核RBF使用最为普遍。可以发现，全连接法的邻接矩阵保留的信息最为完整，除主对角线元素外，其他元素值都大于1，因此，全连接法的使用也最为普遍。

有了邻接矩阵以后，我们就可以开始下一步的工作了。不过在此之前，我们还需要引入一个比较简单的概念——度矩阵。对于图中的任意一个点 ，它的度  定义为和它相连的所有边权重之和，即:

                                                 

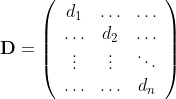
所有样本点的度组成的矩阵 D 称之为度矩阵：

                                                 

可以发现度矩阵是一个对角矩阵，只有主对角线元素有值（非零），对应第 i 个元素的度。

1.3 拉普拉斯矩阵

你可能会奇怪为何么会在这里介绍拉普拉斯矩阵，因为后面的切图算法和这个矩阵的性质息息相关。当然了，不要被拉普拉斯的名字吓到，这个矩阵的计算非常简单：

                                                 

是的，拉普拉斯矩阵就是前面的度矩阵减去权重的邻接矩阵即可。不过我们还要介绍一些关于拉普拉斯矩阵的性质，因为它有助于我们理解后面的切图算法。

1. 拉普拉斯矩阵是对称矩阵，因为 D 和 W 都是对称矩阵。
2. 由于拉普拉斯矩阵是对称矩阵，它的所有的特征值都是大于等于0的实数，且特征向量两两正交（可参考线性代数的有关内容，记住即可）。
3. 对于任意的列向量 f，我们有：

                                                 

证明过程如下：

                                                 

                                                    

上式最后一步由1.2节  的定义可以很容易得到。

1.4 谱聚类切图

 

对于无向图G的切图，我们的目标是将图G(V,E)切成相互没有连接的k个子图，k个子图点的集合分别为：。显然，，。则任意切图子集A和B之间的切图边权重和为：

                                                 。

k 个子图切图边权重和为：

                                                 

其中  为  的补集。

在选择切图的路线时，我们自然倾向于选择那些权重较低的边，回到我们上面的切图权重公式，恰好就是最小化 cut 。但是这似乎还存在一些问题，我们保证了子图之间的边权重最小，但是子图内部的权重我们并没有考量，而且这种方式会更加倾向于切割边缘点的连接边。因为一般边缘点的连接边最少，更容易得到最小的权重值，且切割最方便。

为了解决这些问题，谱聚类主要有两种切图优化算法：RatioCut和Ncut。下面详细介绍这两种切法。

1. RatioCut

RatioCut为了避免最小化切图引入了子图点的个数，即：

                                                

 表示子集中的样本点个数。那么怎么最小化这个RatioCut函数呢？又引入了子集  的指示向量 ，其中 j = 1,2,3...k， 是一个n维向量（n是样本数），定义为：

                                                

简单地说就是每个子集  对应一个指示向量 ， 中的每个元素，分别代表 n 个样本点的指示结果，如果在原始数据中第 i 个样本被分割到子集  中，则  的第 i 个元素为 ，否则为0。则：

                                              

                                              

                                              

                                              

                                              

注意上式的第二步， 时，  和  都等于 ， 时，  和  都等于 0。

是不是很神奇，对于子图 i ，它的RatioCut等于 。令 ，那么k个子图的RatioCut等于：

                                              

tr 表示矩阵的迹，值为矩阵主对角线元素的和。我们现在的目标转化为了最小化一个矩阵的迹。可以发现，H 的所有列向量，即 ，是一组标准正交基（每个  都有  个值为  的元素，其他都为0），所以：。L 是很容易计算的，因此我们的任务进一步细化为找到合适的 H 。对于 n 很大的数据，这无疑是灾难性的NP-hard问题，显然我们不可能靠遍历求解。进一步观察发现，L 为对称矩阵，也就是说  的最大值是 L 的最大特征值，最小值是 L 的最小特征值（可参考线性代数和PCA的相关内容）。在PCA中，我们的目标是找到协方差矩阵（对应此处的拉普拉斯矩阵L）的最大的特征值，而在谱聚类中，我们的目标是找到 L 的最小特征值，得到对应的特征向量，此时对应二分切图效果最佳。也就是说，我们这里要用到维度规约（降维）的思想来近似去解决这个NP难的问题。也就是说对于 ，我们的目标变成了找到 L 的k个最小的特征值，一般来说，k远远小于n，也就是说，此时我们进行了维度规约，将维度从n降到了k，从而近似可以解决这个NP难的问题。这k个特征值对应的k个特征向量组成的 （k,n）大小的矩阵就是 H。现在我们的NP-hard问题转化为了求一个矩阵的特征值和特征向量问题，如果不理解这个过程，也没关系，知道这个结果就可以了。例如，我们之前设定的向量的元素值取值只有两种可能，但是我们求得的特征向量未必是满足的，这里涉及到泛函变分等较为复杂的数学知识求得近似解，有兴趣的可以查阅相关资料。

最后，我们还需要对 H 按行做标准化处理：

                                             

由于我们在使用维度规约的时候损失了少量信息，导致得到的优化后的指示向量h对应的 H 不能完全指示各样本的归属，因此一般在得到 H 后还需要对每一行进行一次传统的聚类，比如K-Means等。注意我们的目标并不是为了求得最小的 ，而是对应最小迹的 H，所以聚类的时候，分别对H中的行进行聚类即可。因为：① H 除了是能满足极小化条件的解，还是 L 的特征向量，也可以理解为 W 的特征向量，而 W 则是我们构造出的图，对该图的特征向量做聚类，一方面聚类时不会丢失原图太多信息，另一方面是降维加快计算速度，而且容易发现图背后的模式；② 之前定义的指示向量  是二值分布，但是由于NP-hard问题的存在导致  无法显式求解，只能利用特征向量进行近似逼近，但是特征向量是取任意值，相当于我们对  的二值分布限制进行放松，但这样一来  就无法指示各样本的所属情况（但是相似的样本，特征向量值依然相近）？所以就可以利用kmeans对该向量进行聚类，如果是 k=2 的情况，那么kmeans结果就与之前二值分布的想法相同了，所以kmeans的意义在此。可以参考sklearn官网对SpectralClustering的一句描述：

SpectralClustering performs a low-dimension embedding of the affinity matrix between samples, followed by clustering, e.g., by KMeans.

2. Ncut

Ncut的处理方法和RatioCut非常类似，不同点在于Ncut引入了子图权重 （子图中所有节点的度和），而不是 ，所以：

                                             

同样对指示向量也同步做了改进：

                                             

同样计算：

                                             

                                             

                                             

                                             

                                             

也就是说，我们的优化目标仍然是：

                                            

但是需要注意，此时 H 的列向量不再是标准正交基，因为  不再是单位向量，也就是说 ，但是 。证明如下：

                                            

                                             

                                            

可以发现，除了 H 的限制条件，Ncut的极小化与Ratiocut的极小化基本无差异，也就是这个限制使得RatioCut里面的降维思想在这里不能再直接用。我们对 H 做一个简单的变换：。则：

                                            

                                            

现在是不是感觉似曾相似了，回到了Ratiocut的路线上。现在，我们只需要计算出  的最小k个特征值对应特征向量就可以了（相当于对D开方再求逆矩阵）。然后按行进行标准化，并使用k-means等聚类算法按行进行聚类即可。

其实， 相当于对拉普拉斯矩阵 L 做了一次标准化：。这么做的一个好处就是对L中的元素进行标准化处理使得不同元素的量纲得到归一，具体理解就是，同个子集里，不同样本点之间的连边可能大小比较相似，这点没问题，但是对于不同子集，样本点之间的连边大小可能会差异很大，做 这一步normalize操作，可以将L中的元素归一化在[-1,1]之间，这样量纲一致，对算法迭代速度，结果的精度都是有很大提升。

1.5 总结

可以发现，虽然我们介绍谱聚类原理的篇幅较多，但是实际最终的计算确很简单。谱聚类主要流程如下;

1. 根据输入样本集构建邻接权重矩阵 W，进而构架你度矩阵 D 和拉普拉斯矩阵 L
2. 如果选择Ncut作为切图方法，构建标准化后的拉普拉斯矩阵 
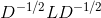
3. 计算拉普拉斯矩阵最小的 k 个特征值以及对应的 k 个特征向量
4. 将特征向量 f 组成的矩阵 H （或者F）按行标准化，最终组成 n×k 维的特征矩阵
5. 将特征矩阵中的每一行作为一个样本使用k-means等方法进行聚类得到结果

谱聚类的主要优点：

1. 谱聚类只需要数据之间的相似度矩阵（权重矩阵），因此对于处理稀疏数据的聚类很有效。这点传统聚类算法比如K-Means很难做到
2. 由于使用了降维，因此在处理高维数据聚类时的复杂度比传统聚类算法好

谱聚类的主要缺点：

1. 如果最终聚类的维度非常高，则由于降维的幅度不够，谱聚类的运行速度和最后的聚类效果均不好
2. 聚类效果依赖于相似矩阵（1.2节不同的构建方法），不同的相似矩阵得到的最终聚类效果可能很不同
3. 适合处理簇数不大的场景

二、实践

本节，我们同样通过sklearn来学习谱聚类的使用，sklearn的谱聚类默认只实现了Ncut切图方法。

2.1 API

谱聚类的API定义如下：

sklearn.cluster.SpectralClustering(n_clusters=8,   ##聚类簇数，也是投影子空间的维数（H矩阵的列大小）
*, 
eigen_solver=None,  ## 计算拉普拉斯矩阵特征值/特征向量时的方法，默认None表示使用‘arpack’。对于非常大、稀疏的邻接矩阵，可以使用‘amg’，计算会更快，但可能会不稳定，并且需要安装 pyamg。当速度可以接受时，默认即可
n_components=None,  ## 谱嵌入时使用的拉普拉斯矩阵的特征向量个数，默认等于n_clusters
random_state=None, 
n_init=10,          ## kmeans算法初始化种子的运行次数，同K-Means类里面的n_init
gamma=1.0,          ## 下文rbf, poly, sigmoid, laplacian and chi2核函数中 γ
affinity='rbf',     ## 邻接矩阵（权重矩阵）的构建方法
                    ## 默认‘rbf’表示全连接法中的高斯核函数，一般都默认使用‘rbf’
                    ## ‘linear线性核函数’
                    ## ‘poly’多项式核函数
                    ## ‘sigmoid’即sigmoid核函数
                    ## ‘nearest_neighbors’表示k近邻法
                    ## ‘precomputed’表示fit的X是计算好的邻接矩阵
                    ## ‘precomputed_nearest_neighbors’表示fit的X是计算好的近邻稀疏矩阵
                    ## 也可以自定义邻接矩阵的计算方法，即传入一个回调函数
n_neighbors=10,     ## 使用近邻法时的k
eigen_tol=0.0,      ## 当eigen_solver='arpack'时，矩阵分解停止的条件
assign_labels='kmeans', ## 最终的聚类策略，可选 'kmeans' 和 'discretize'。kmeans聚类效果更好，但kmeans结果受初始值选择的影响，可能每次都不同，复现比较麻烦（也可以设置random_state值不变保持稳定），discretize 相对就不那么敏感
degree=3,           ## 若affinity='poly'即多项式核，表示多项式核的次数，下文多项式核公式中的 d
coef0=1,            ## 下文多项式核和sigmoid核中的常数项（偏执项）r
kernel_params=None, ## 若自定义affinity，该参数用来给回调函数传参
n_jobs=None, 
verbose=False)

多项式核函数形式：

高斯核函数形式：

sigmoid核函数形式：

另外，高斯核函数也为我们提供了一种转换思想，对于距离矩阵（0表示相同的点，更大的值表示相差较大的点），可以较为方便的转换为邻接矩阵（相似矩阵）：

np.exp(- dist_matrix ** 2 / (2. * delta ** 2))

2.2 案例

生成500个6维的数据集，分为5个簇。因为是高斯核函数，对 n_clusters 和 gamma 调参。

import numpy as np
from sklearn import datasets
from sklearn.cluster import SpectralClustering
from sklearn import metrics

X, y = datasets.make_blobs(n_samples=500, n_features=6, centers=5, cluster_std=[0.4, 0.3, 0.4, 0.3, 0.4], random_state=11)


y_pred = SpectralClustering().fit_predict(X)
print("Calinski-Harabasz Score", metrics.calinski_harabasz_score(X, y_pred))

for index, gamma in enumerate((0.01,0.1,1,10)):
    for index, k in enumerate((3,4,5,6)):
        y_pred = SpectralClustering(n_clusters=k, gamma=gamma).fit_predict(X)
        print("Calinski-Harabasz Score with gamma=", gamma, "n_clusters=", k,"score:", metrics.calinski_harabasz_score(X, y_pred))

另外，sklearn也提供了一个不同聚类算法比较的综合案例，可以参考下。

参考资料

[1] https://www.cnblogs.com/pinard/p/6221564.html

[2] https://blog.csdn.net/yc_1993/article/details/52997074