人工智能系列实验（二）——用于区分不同颜色区域的浅层神经网络

本实验利用Python，搭建了一个用于区分不同颜色区域的浅层神经网络。通过学习已有的点坐标及其对应颜色，从而绘制不同颜色区域的分界线，预测各个区域的颜色。

实验环境： python中numpy、matplotlib和sklearn库

import numpy as np
import matplotlib.pyplot as plt
import sklearn  # 用于数据挖掘、数据分析和机器学习
import sklearn.linear_model

训练样本： 400个带颜色点的二维坐标

测试样本： 同训练样本。为简便起见，只用训练数据集进行效果检验。

关于本实验完整代码详见：
https://github.com/PPPerry/AI_projects/tree/main/2.colored_areas_distinguish

构建的神经网络模型如下：

我们的目标就是通过训练这个神经网络来通过坐标值判断在坐标系中某一点可能的颜色，例如坐标(-4, 2)的点最可能是什么颜色，(1, -2)最可能是什么颜色。将红色和蓝色的点的区域区分出来。

基于该神经网络模型，代码实现如下：

首先，加载训练数据。

def load_planar_dataset():
    """
    生成二维花瓣形样本点
    :return: 样本坐标, 样本颜色
    """
    m = 400  # 样本数
    N = int(m / 2)  # 各类样本数
    D = 2  # 维度
    X = np.zeros((m, D))  # 400行2列，每一行是一个样本
    Y = np.zeros((m, 1), dtype='uint8')  # 标签向量，0代表红色，1代表蓝色

    for j in range(2):
        ix = range(N * j, N * (j + 1))
        t = np.linspace(j * 3.12, (j + 1) * 3.12, N) + np.random.randn(N) * 0.2  # theta
        r = 10 * np.sin(4 * t) + np.random.randn(N) * 0.2  # radius
        X[ix] = np.c_[r * np.sin(t), r * np.cos(t)]
        Y[ix] = j

    X = X.T
    Y = Y.T

    return X, Y


X, Y = load_planar_dataset()

# X[0, :]表示400点的横坐标，X[1, :]表示纵坐标，c=Y.ravel()是指定400个点的颜色，s=40指定点的大小
# cmap指定调色板，如果用不同的调色板，那么Y的值对应 的颜色也会不同，用plt.cm.Spectral这个调色板时，0指代红色，1指代蓝色
plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral)  # squeeze函数与ravel函数效果相同
plt.ylabel('y')
plt.xlabel('x')
plt.show()

我们没有用真实的数据集，而是用代码生成了一些总体形状是花瓣状的虚拟数据集。
绘制数据集如下：

其次，构造神经网络中用到的相应函数。

def initialize_parameters(n_x, n_h, n_y):
    """
    初始化参数w和b
    :param n_x: 输入层的神经元个数
    :param n_h: 隐藏层的神经元个数
    :param n_y: 输出层的神经元个数
    :return: 初始化的参数
    """
    # 随机初始化第一层（隐藏层）的参数，每一个隐藏层神经元都与输入层的每一个神经元相连
    W1 = np.random.randn(n_h, n_x) * 0.01  # W1的维度是(隐藏层的神经元个数, 输入层的神经元个数)
    b1 = np.zeros((n_h, 1))  # b1的维度是(隐藏层的神经元个数, 1)

    # 随机初始化第二层（输出层）的参数
    W2 = np.random.randn(n_y, n_h) * 0.01
    b2 = np.zeros((n_y, 1))

    parameters = {
        "W1": W1,
        "b1": b1,
        "W2": W2,
        "b2": b2
    }
    return parameters


def sigmoid(z):
    """
    sigmod函数实现
    :param z: 数值或一个numpy数组
    :return: [0, 1]范围数值
    """
    s = 1 / (1 + np.exp(-z))
    return s


def forward_propagation(X, parameters):
    """
    前向传播
    :param X: (2, 400)的输入层样本
    :param parameters: 参数
    :return: 输出层的输出，中间变量
    """
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']

    Z1 = np.dot(W1, X) + b1
    A1 = np.tanh(Z1)  # 第一层的激活函数使用tanh。numpy库中自带。
    Z2 = np.dot(W2, A1) + b2
    A2 = sigmoid(Z2)  # 第二层的激活函数用sigmoid

    # 保存中间变量，在反向传播时会用到
    cache = {
        "Z1": Z1,
        "A1": A1,
        "Z2": Z2,
        "A2": A2
    }
    return A2, cache


def compute_cost(A2, Y, parameters):
    """
    计算成本
    :param A2: 输出层的输出
    :param Y: 样本颜色
    :param parameters: 参数
    :return: 成本
    """
    m = Y.shape[1]

    logprobs = np.multiply(Y, np.log(A2)) + np.multiply((1 - Y), np.log(1 - A2))
    cost = - np.sum(logprobs) / m

    return cost


def backward_propagation(parameters, cache, X, Y):
    """
    反向传播
    :param parameters: 参数
    :param cache: 中间变量
    :param X: 样本坐标
    :param Y: 样本颜色
    :return: 梯度
    """
    m = X.shape[1]

    W1 = parameters['W1']
    W2 = parameters['W2']

    A1 = cache['A1']
    A2 = cache['A2']

    dZ2 = A2 - Y
    dW2 = (1 / m) * np.dot(dZ2, A1.T)
    db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)
    dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2))
    dW1 = (1 / m) * np.dot(dZ1, X.T)
    db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)

    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}

    return grads


def update_parameters(parameters, grads, learning_rate=1.0):
    """
    梯度下降
    :param parameters: 参数
    :param grads: 梯度
    :param learning_rate: 学习率
    :return: 更新后的参数
    """
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']

    dW1 = grads['dW1']
    db1 = grads['db1']
    dW2 = grads['dW2']
    db2 = grads['db2']

    W1 = W1 - learning_rate * dW1
    b1 = b1 - learning_rate * db1
    W2 = W2 - learning_rate * dW2
    b2 = b2 - learning_rate * db2

    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}

    return parameters

在人工智能系列实验（一）中，我们初始化单神经元网络时，初始化参数均为0。但是在多层神经网络中必须随机初始化，若一层中各神经元初始化参数均相同，则该层实际效果只相当于一个神经元。
最终，组合以上函数，构建出最终的神经网络模型函数以及利用模型的预测函数。

def nn_module(X, Y, n_h, num_iterations=10001, print_cost=False):
    """
    构建神经网络模型
    :param X: 样本坐标
    :param Y: 样本颜色
    :param n_h: 隐藏层的神经元个数
    :param num_iterations: 迭代次数
    :param print_cost: 是否打印成本
    :return: 参数
    """
    n_x = X.shape[0]  # 输入层的神经元个数
    n_y = Y.shape[0]  # 输出层的神经元个数

    # 初始化参数
    parameters = initialize_parameters(n_x, n_h, n_y)
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']

    for i in range(0, num_iterations):
        # 前向传播
        A2, cache = forward_propagation(X, parameters)

        # 计算成本
        cost = compute_cost(A2, Y, parameters)

        # 反向传播
        grads = backward_propagation(parameters, cache, X, Y)

        # 更新参数
        parameters = update_parameters(parameters, grads)

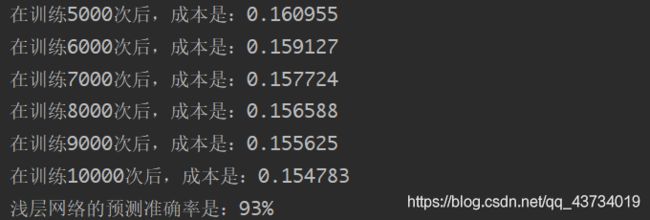
        if print_cost and i % 1000 == 0:
            print("在训练%i次后，成本是：%f" % (i, cost))

    return parameters
  
    
def predict(parameters, X):
    """
    利用模型预测
    :param parameters: 参数
    :param X: 样本坐标
    :return: 预测的样本颜色
    """
    A2, cache = forward_propagation(X, parameters)
    predictions = np.round(A2)

    return predictions

现在调用上面的模型函数对我们最开始加载的数据进行训练和预测。

parameters = nn_module(X, Y, n_h=5, num_iterations=10001, print_cost=True)

predictions = predict(parameters, X)
print('浅层网络的预测准确率是：%d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')

输出：优化10000次后的成本是0.1548。对训练数据的准确率为93%左右。

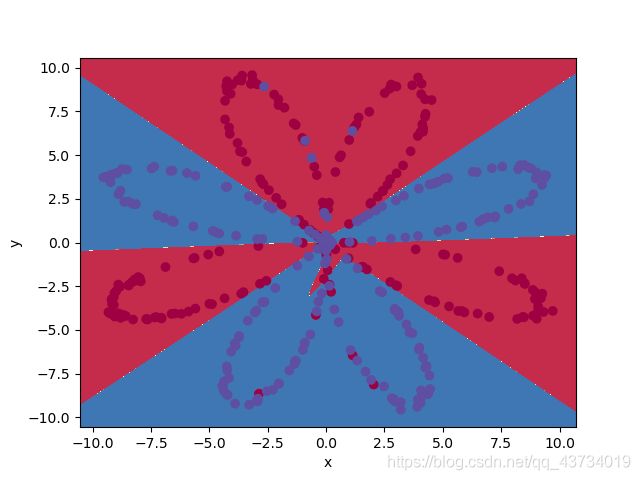
最后，构造绘制边界线函数，可视化各颜色区域的预测结果。

def plot_decision_boundary(model, X, y):
    """
    绘制区分颜色区域的分界线
    :param model: 预测函数
    :param X: 样本坐标
    :param y: 样本颜色
    :return:
    """
    x_min = X[0, :].min() - 1
    x_max = X[0, :].max() + 1
    y_min = X[1, :].min() - 1
    y_max = X[1, :].max() + 1
    h = 0.01
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

    Z = model(np.c_[xx.ravel(), yy.ravel()])  # 预测整张画布上各个点的颜色
    Z = Z.reshape(xx.shape)  # 转换为(1, 400)

    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)  # 这里仅需要找出分界线后填充，故使用等高线绘制，用时远小于使用散点图scatter绘制
    plt.ylabel('y')
    plt.xlabel('x')
    plt.scatter(X[0, :], X[1, :], c=y, cmap=plt.cm.Spectral)
    plt.show()


# 绘制预测结果
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y.ravel())

绘制结果如下：

进一步实验得到的结论：

1. 单神经元网络与浅层网络的预测效果对比

在人工智能系列实验（一）中，我们构建了一个单神经元网络来识别图中是否为猫。在本实验中，我们不妨也构建一个单神经元网络来完成同样的区分不同颜色区域的任务，从而比较两个网络的预测效果。

上一个实验，我们为了实现单神经元网络写了很多原理性的底层代码，其实如果利用sklearn这个库的话，几行代码就够了。

# 生成单神经元网络并训练
clf = sklearn.linear_model.LogisticRegressionCV()  # 生成LogisticRegressionCV类的一个对象，LogisticRegressionCV类内部实现了一个单神经元网络
clf.fit(X.T, Y.T.ravel())  # 这个方法会根据数据集进行训练，并将训练好的w和b参数保存在对象clf中

single_predict = clf.predict(X.T)  # 对400个样本点的颜色预测结果
print('单神经元的预测准确率是：' + str(clf.score(X.T, Y.T.ravel()) * 100) + '%')

plot_decision_boundary(lambda x: clf.predict(x), X, Y.ravel())

输出：单神经元的预测准确率是：51.5%。

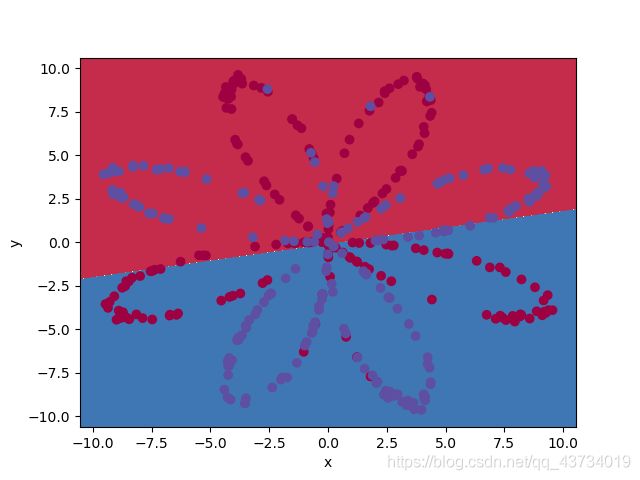
可见，单神经元网络只是简单地认为坐标上部的点是红色，但实际上上面还有很多蓝色点，而且下面也有很多红色点。
结论：相比于单神经元网络，浅层网络对训练数据的准确率为93%左右，效果提升显著。

2. 不同的隐藏层神经元个数对应的准确度对比

hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50]
for i, n_h in enumerate(hidden_layer_sizes):
    parameters = nn_module(X, Y, n_h, num_iterations=5000, print_cost=False)
    predictions = predict(parameters, X)
    accuracy = float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100)
    print("{}个隐藏层神经元时的准确度是: {} %".format(n_h, accuracy))

输出：
1个隐藏层神经元时的准确度是:   70.0 %
2个隐藏层神经元时的准确度是:   68.0 %
3个隐藏层神经元时的准确度是:   94.5 %
4个隐藏层神经元时的准确度是:   94.5 %
5个隐藏层神经元时的准确度是:   94.5 %
20个隐藏层神经元时的准确度是: 94.5 %
50个隐藏层神经元时的准确度是: 94.8 %
结论：一般来说，相同训练次数时，神经元个数越多，预测准确度越好。

结束语：

1. 实验过程中，一定要搞清楚变量的维度，否则做数据处理、写数组操作时会容易出现问题。
2. 本实验与人工智能系列实验（一）均采用几乎基于纯Python的numpy库函数进行神经网络模型的搭建，目的是理解神经网络背后的数学原理及意义。我们也当然可以像实验末部分，利用sklearn库函数快速构建浅层神经网络。在后续的实验中，我也会对TensorFlow等经典框架进行学习与运用。
3. 相关代码可能会不断更新改进，以github中的代码为准。
4. 在本实验中，我们可以明显看到，多加一层隐藏层后的神经网络的效果要远远优于单神经元网络。后续还会更新深层神经网络等，进一步强化神经网络的性能。

往期人工智能系列实验：

人工智能系列实验（一）——用于识别猫的二分类单层神经网络