DataMining-系统聚类

（2017-05-01 银河统计）

系统聚类

  系统聚类，即层次聚类法。先计算样本之间的距离，每次将距离最近的点合并到同一个类。然后，再计算类与类之间的距离，将距离最近的类合并为一个大类。最终经过不停的合并，直到合成了一个类。

  正如样本之间的距离可以有不同的定义方法一样（欧氏距离、曼哈顿距离、马氏距离等），类与类之间的距离也有各种定义。例如可以定义类与类之间的距离为两类之间最近样本的距离，或者定义为两类之间最远样本的距离，也可以定义为两类重心之间的距离等等。类与类之间用不同的方法定义距离，就产生了不同的系统聚类方法。常用的系统聚类方法，即最短距离法、最长距离法、中间距离法、重心法、类平均法、可变类平均法、相似法、离差平方和法。系统聚类分析尽管方法很多，但归类的步骤基本上是一样的，所不同的仅是类与类之间的距离有不同的定义方法，从而得到不同的计算距离的公式。

  原理详细讲解和网页（JS）计算实现，见银河统计系统聚类法 - 数据挖掘算法。

  R和Python计算实现见下文。

目录概览

 1)R语言实战

 2)Python实战

 3)R语言函数总结

 4)Python函数总结

---

 

• Data - 鸢尾花iris数据集介绍

  Iris也称鸢尾花卉数据集，是一类多重变量分析的数据集。通过花萼长度，花萼宽度，花瓣长度，花瓣宽度4个属性预测鸢尾花卉属于（Setosa，Versicolour，Virginica）三个种类中的哪一类。鸢尾花(iris)是数据挖掘常用到的一个数据集，包含150种鸢尾花的信息，每50种取自三个鸢尾花种之一（setosa,versicolour或virginica)。每个花的特征用下面的5种属性描述萼片长度(Sepal.Length)、萼片宽度(Sepal.Width)、花瓣长度(Petal.Length)、花瓣宽度(Petal.Width)、类(Species)。

ID	Sepal.Length	Sepal.Width	Petal.Length	Petal.Width	Species
1	5.1	3.5	1.4	0.2	setosa
2	4.9	3.0	1.4	0.2	setosa
3	4.7	3.2	1.3	0.2	setosa
4	4.6	3.1	1.5	0.2	setosa
5	5.0	3.6	1.4	0.2	setosa
6	5.4	3.9	1.7	0.4	setosa
7	4.6	3.4	1.4	0.3	setosa
8	5.0	3.4	1.5	0.2	setosa
9	4.4	2.9	1.4	0.2	setosa
10	4.9	3.1	1.5	0.1	setosa
11	5.4	3.7	1.5	0.2	setosa
12	4.8	3.4	1.6	0.2	setosa
13	4.8	3.0	1.4	0.1	setosa
14	4.3	3.0	1.1	0.1	setosa
15	5.8	4.0	1.2	0.2	setosa
16	5.7	4.4	1.5	0.4	setosa
17	5.4	3.9	1.3	0.4	setosa
18	5.1	3.5	1.4	0.3	setosa
19	5.7	3.8	1.7	0.3	setosa
20	5.1	3.8	1.5	0.3	setosa
21	5.4	3.4	1.7	0.2	setosa
22	5.1	3.7	1.5	0.4	setosa
23	4.6	3.6	1.0	0.2	setosa
24	5.1	3.3	1.7	0.5	setosa
25	4.8	3.4	1.9	0.2	setosa
26	5.0	3.0	1.6	0.2	setosa
27	5.0	3.4	1.6	0.4	setosa
28	5.2	3.5	1.5	0.2	setosa
29	5.2	3.4	1.4	0.2	setosa
30	4.7	3.2	1.6	0.2	setosa
31	4.8	3.1	1.6	0.2	setosa
32	5.4	3.4	1.5	0.4	setosa
33	5.2	4.1	1.5	0.1	setosa
34	5.5	4.2	1.4	0.2	setosa
35	4.9	3.1	1.5	0.2	setosa
36	5.0	3.2	1.2	0.2	setosa
37	5.5	3.5	1.3	0.2	setosa
38	4.9	3.6	1.4	0.1	setosa
39	4.4	3.0	1.3	0.2	setosa
40	5.1	3.4	1.5	0.2	setosa
41	5.0	3.5	1.3	0.3	setosa
42	4.5	2.3	1.3	0.3	setosa
43	4.4	3.2	1.3	0.2	setosa
44	5.0	3.5	1.6	0.6	setosa
45	5.1	3.8	1.9	0.4	setosa
46	4.8	3.0	1.4	0.3	setosa
47	5.1	3.8	1.6	0.2	setosa
48	4.6	3.2	1.4	0.2	setosa
49	5.3	3.7	1.5	0.2	setosa
50	5.0	3.3	1.4	0.2	setosa
51	7.0	3.2	4.7	1.4	versicolor
52	6.4	3.2	4.5	1.5	versicolor
53	6.9	3.1	4.9	1.5	versicolor
54	5.5	2.3	4.0	1.3	versicolor
55	6.5	2.8	4.6	1.5	versicolor
56	5.7	2.8	4.5	1.3	versicolor
57	6.3	3.3	4.7	1.6	versicolor
58	4.9	2.4	3.3	1.0	versicolor
59	6.6	2.9	4.6	1.3	versicolor
60	5.2	2.7	3.9	1.4	versicolor
61	5.0	2.0	3.5	1.0	versicolor
62	5.9	3.0	4.2	1.5	versicolor
63	6.0	2.2	4.0	1.0	versicolor
64	6.1	2.9	4.7	1.4	versicolor
65	5.6	2.9	3.6	1.3	versicolor
66	6.7	3.1	4.4	1.4	versicolor
67	5.6	3.0	4.5	1.5	versicolor
68	5.8	2.7	4.1	1.0	versicolor
69	6.2	2.2	4.5	1.5	versicolor
70	5.6	2.5	3.9	1.1	versicolor
71	5.9	3.2	4.8	1.8	versicolor
72	6.1	2.8	4.0	1.3	versicolor
73	6.3	2.5	4.9	1.5	versicolor
74	6.1	2.8	4.7	1.2	versicolor
75	6.4	2.9	4.3	1.3	versicolor
76	6.6	3.0	4.4	1.4	versicolor
77	6.8	2.8	4.8	1.4	versicolor
78	6.7	3.0	5.0	1.7	versicolor
79	6.0	2.9	4.5	1.5	versicolor
80	5.7	2.6	3.5	1.0	versicolor
81	5.5	2.4	3.8	1.1	versicolor
82	5.5	2.4	3.7	1.0	versicolor
83	5.8	2.7	3.9	1.2	versicolor
84	6.0	2.7	5.1	1.6	versicolor
85	5.4	3.0	4.5	1.5	versicolor
86	6.0	3.4	4.5	1.6	versicolor
87	6.7	3.1	4.7	1.5	versicolor
88	6.3	2.3	4.4	1.3	versicolor
89	5.6	3.0	4.1	1.3	versicolor
90	5.5	2.5	4.0	1.3	versicolor
91	5.5	2.6	4.4	1.2	versicolor
92	6.1	3.0	4.6	1.4	versicolor
93	5.8	2.6	4.0	1.2	versicolor
94	5.0	2.3	3.3	1.0	versicolor
95	5.6	2.7	4.2	1.3	versicolor
96	5.7	3.0	4.2	1.2	versicolor
97	5.7	2.9	4.2	1.3	versicolor
98	6.2	2.9	4.3	1.3	versicolor
99	5.1	2.5	3.0	1.1	versicolor
100	5.7	2.8	4.1	1.3	versicolor
101	6.3	3.3	6.0	2.5	virginica
102	5.8	2.7	5.1	1.9	virginica
103	7.1	3.0	5.9	2.1	virginica
104	6.3	2.9	5.6	1.8	virginica
105	6.5	3.0	5.8	2.2	virginica
106	7.6	3.0	6.6	2.1	virginica
107	4.9	2.5	4.5	1.7	virginica
108	7.3	2.9	6.3	1.8	virginica
109	6.7	2.5	5.8	1.8	virginica
110	7.2	3.6	6.1	2.5	virginica
111	6.5	3.2	5.1	2.0	virginica
112	6.4	2.7	5.3	1.9	virginica
113	6.8	3.0	5.5	2.1	virginica
114	5.7	2.5	5.0	2.0	virginica
115	5.8	2.8	5.1	2.4	virginica
116	6.4	3.2	5.3	2.3	virginica
117	6.5	3.0	5.5	1.8	virginica
118	7.7	3.8	6.7	2.2	virginica
119	7.7	2.6	6.9	2.3	virginica
120	6.0	2.2	5.0	1.5	virginica
121	6.9	3.2	5.7	2.3	virginica
122	5.6	2.8	4.9	2.0	virginica
123	7.7	2.8	6.7	2.0	virginica
124	6.3	2.7	4.9	1.8	virginica
125	6.7	3.3	5.7	2.1	virginica
126	7.2	3.2	6.0	1.8	virginica
127	6.2	2.8	4.8	1.8	virginica
128	6.1	3.0	4.9	1.8	virginica
129	6.4	2.8	5.6	2.1	virginica
130	7.2	3.0	5.8	1.6	virginica
131	7.4	2.8	6.1	1.9	virginica
132	7.9	3.8	6.4	2.0	virginica
133	6.4	2.8	5.6	2.2	virginica
134	6.3	2.8	5.1	1.5	virginica
135	6.1	2.6	5.6	1.4	virginica
136	7.7	3.0	6.1	2.3	virginica
137	6.3	3.4	5.6	2.4	virginica
138	6.4	3.1	5.5	1.8	virginica
139	6.0	3.0	4.8	1.8	virginica
140	6.9	3.1	5.4	2.1	virginica
141	6.7	3.1	5.6	2.4	virginica
142	6.9	3.1	5.1	2.3	virginica
143	5.8	2.7	5.1	1.9	virginica
144	6.8	3.2	5.9	2.3	virginica
145	6.7	3.3	5.7	2.5	virginica
146	6.7	3.0	5.2	2.3	virginica
147	6.3	2.5	5.0	1.9	virginica
148	6.5	3.0	5.2	2.0	virginica
149	6.2	3.4	5.4	2.3	virginica
150	5.9	3.0	5.1	1.8	virginica

 

---

1)R语言实战

1.1 R语言相关函数详解

系统聚类(Hierarchical Method)主要运用到了stats包（R语言内置包）中的hclust()；cutree()；rect.hclust()三个函数和绘图函数plot()。

    - hclust(d, method="complete", members=NULL)
    - cutree(tree, k=NULL, h=NULL) 
    - plot(hc.r, hang=-1, labels=NULL) 或者 plot(hc.r, hang=0.1, labels=F)
    - rect.hclust(tree, k=NULL, which=NULL, x=NULL, h=NULL, border=2, cluster=NULL ) 

r语言中使用 hclust(d, method="complete", members=NULL) 来进行层次聚类，计算各种类与类之间的距离，其中d为距离矩阵，而method表示类的合并方法，有：

    - single     最短距离法
    - complete   最长距离法
    - median     中间距离法
    - mcquitty   相似法
    - average    类平均法
    - centroid   重心法
    - ward.D2    离差平方和法

r语言中使用 cutree(tree, k=NULL, h=NULL) 从hclust的结果对象中提取每个簇中的成员，其中 k 表示将簇中对象分成几类，h 表示削减树的高度值（通过高度值来确定分成几类）。

r语言中使用 plot(hc.r, hang=-1, labels=NULL) 对聚类结果进行绘图，其中 hang 等于数值，表示标签与末端树杈之间的距离，若是负数，则表示末端树杈长度是0，即标签对齐。而 labels 表示标签，默认是NULL，表示变量原有名称，labels=F：表示不显示标签。

r语言中使用 rect.hclust() 函数可以在plot()形成的系谱图中将指定类别中的样本分支用方框表示出来。其中 tree 表示一个hclust对象，k 指定要聚类的个数， border指定图中边界的颜色。

通过查看R帮助文档可以进一步理解函数各个参数的用法：

    # ?hclust 1
    hc <- hclust(dist(USArrests), "ave")
    plot(hc)
    plot(hc, hang = -1)
    
    # ?hclust 2
    hc <- hclust(dist(USArrests)^2, "cen")
    memb <- cutree(hc, k = 10)
    cent <- NULL
    for(k in 1:10){
      cent <- rbind(cent, colMeans(USArrests[memb == k, , drop = FALSE]))
    }
    hc1 <- hclust(dist(cent)^2, method = "cen", members=table(memb))
    opar <- par(mfrow = c(1, 2))
    plot(hc,  labels = FALSE, hang = -1, main = "Original Tree")
    plot(hc1, labels = FALSE, hang = -1, main = "Re-start from 10 clusters")
    par(opar)

    # ?cutree
    hc <- hclust(dist(USArrests))
    cutree(hc, k=1:5) # k = 1 is trivial[K = 1是微不足道]
    cutree(hc, h=20)
    
    # ?rect.hclust
    hca <- hclust(dist(USArrests))
    plot(hca)
    rect.hclust(hca, k = 3, border = "red")
    x <- rect.hclust(hca, h = 50, which = c(2,7), border = 3:4)
    x

注意：当用已知距离矩阵进行聚类时，即变量间的距离已经计算完，只是想用已知的距离矩阵进行聚类。这时，需将距离矩阵转成dist类型。然后再执行hclust()聚类和plot()画图。

    # mydata作为距离矩阵,且为正方矩阵
    mydata<-matrix(1:25,ncol=5); 
    class(mydata); 
    # 把mydata变成dist类型
    mydist <- as.dist(mydata);
    class(mydist);
    [1] "dist"

1.2 R语言对鸢尾花[iris]数据进行系统聚类分析

1.2.1) 系统聚类分析

步骤：

Step1: 复制上文中鸢尾花数据集到剪切板【通过剪切板为中介将数据转换为R环境中的变量】。

Step2: 运行以下程序进行层次（系统）聚类。

    ##################################
    options(digits=4)
    mydata <- read.table("clipboard",header=T)
    class(mydata)
    dim(mydata)
    head(mydata)
    # Data
    iris_model_data <- mydata[,2:4]
    
    # Step1:计算距离（样本和样本 或 变量与变量）
    #  当用已知距离矩阵进行聚类时，即变量间的距离已经计算完，只是想用已知的距离矩阵进行聚类。
    #  这时，需将距离矩阵转成dist类型。使用函数： as.dist()
    d <- dist(iris_model_data, method="euclidean", diag = F)
    
    # Step2:计算类与类之间的距离 - 注意：method方法可以选择
    model <- hclust(d, method='ward.D2')
    
    # Step3:根据hclust结果，选择聚类成几类。
    groups <- cutree(model, k=3)
    
    # Step4:绘制聚类结果
    # plot(model,labels=F,hang=-1)
    plot(model, labels=F, hang=-1, cex=0.6)
    rect.hclust(model, k=3, border=2:4)
    box()
    
    # Step5:查看分组情况
    table(groups,iris$Species)

    # Step6:提取各个分类的详细结果
    print_result <- function(model_data, groups, k) {
      for(i in 1:k){
        print(paste("hclust", i))
        print(model_data[groups==i,])
      }
    }
    print_result(iris_model_data, groups, 3)
    ##################################

采用不同的类间距离进行聚类，相同样本间距离计算方式（euclidean），得到各种聚类结果，如下：

model_name_c	model_name_e	category	result	setosa	versicolor	virginica
最短距离法	single	setosa	1	50	0	0
最短距离法	single	versicolor	2	0	50	48
最短距离法	single	virginica	3	0	0	2
最长距离法	complete	setosa	1	50	0	0
最长距离法	complete	versicolor	2	0	21	49
最长距离法	complete	virginica	3	0	29	1
中间距离法	median	setosa	1	50	0	0
中间距离法	median	versicolor	2	0	38	49
中间距离法	median	virginica	3	0	12	1
相似法	mcquitty	setosa	1	50	0	0
相似法	mcquitty	versicolor	2	0	50	38
相似法	mcquitty	virginica	3	0	0	12
类平均法	average	setosa	1	50	0	0
类平均法	average	versicolor	2	0	50	38
类平均法	average	virginica	3	0	0	12
重心法	centroid	setosa	1	50	0	0
重心法	centroid	versicolor	2	0	46	50
重心法	centroid	virginica	3	0	4	0
离差平方和法	ward.D2	setosa	1	50	0	0
离差平方和法	ward.D2	versicolor	2	0	19	49
离差平方和法	ward.D2	virginica	3	0	31	1

从上表各种聚类结果可知，采用相似法（mcquitty）和类平均法（average）进行系统聚类时，效果是做好的，这两种方法都正确的将鸢尾花的类别setosa和类别versicolor的样本聚到了一类，而将类别virginica的样本聚到了两类中。综合所有聚类方法结果可知，类别为setosa的鸢尾花，都成功聚到了一起，而类别为versicolor和virginica的鸢尾花聚类时混到了一起，说明类别setosa与其它两类差别很大，而类别versicolor与virginica存在一定的相似性，所以采用不用的聚类方法时，这两种类别都是混合存在。

通过对鸢尾花数据进一步分析可知，当保持类间聚类计算方法不变（如：single），而改变样本间距离计算方式，得到的聚类结果基本一致。

1.2.2) 通过对“距离矩阵”绘制热图

步骤：

Step1: 计算得到“距离矩阵” - d

Step2: 绘制热图--更多查看 ?heatmap.2

    ##################################
    library(gplots)
    heatmap.2(as.matrix(d), tracecol=NA)
    # heatmap.2(as.matrix(d), labRow=F, labCol=F, tracecol=NA)
    ##################################

图1.1：“距离矩阵”热图

1.2.3) 为了显示聚类的效果，通过对数据降维，使用ggplot2绘制聚类结果

Step1: 结合多维标度和聚类的结果，先将数据用MDS进行降维

Step2: 以不同的形状表示原来的分类，并用不同的颜色来表示聚类的结果

    ##################################
    mds <- cmdscale(d,k=2,eig=T)
    x <- mds$points[,1]
    y <- mds$points[,2]
    library(ggplot2)
    ggplot(data.frame(x,y),aes(x,y)) + geom_point(size=3,alpha=0.8,aes(colour=factor(result),shape=iris$Species))
    ##################################

图1.2：MDS降维结果图

1.2.4) 使用各种聚类方法进行聚类并绘图

    ##################################
    options(digits=4)
    mydata <- read.table("clipboard",header=T)
    class(mydata)
    dim(mydata)
    head(mydata)
    iris_model_data <- mydata[,2:4]
    d <- dist(iris_model_data, method="manhattan", diag = TRUE, upper = FALSE)
    opar <- par(mfrow = c(3,3))
    method_data <- c('single', 'complete', 'median', 'mcquitty', 'average', 'centroid', 'ward.D2')
    for(i in 1:length(method_data)){
      model <- hclust(d, method=method_data[i])
      plot(model, labels=F, hang=-1, cex=0.6)
      rect.hclust(model, k=3, border=2:4)
      box()
    }
    par(opar)
    ##################################

图1.3：各种聚类方法聚类结果图

1.2.5) 各种谱系图画法

    ##################################
    options(digits=4)
    mydata <- read.table("clipboard",header=T)
    class(mydata)
    dim(mydata)
    head(mydata)
    iris_model_data <- mydata[,2:4]
    d <- dist(iris_model_data, method="manhattan", diag = TRUE, upper = FALSE)
    method_data <- c('single', 'complete', 'median', 'mcquitty', 'average', 'centroid', 'ward.D2')
    for(i in 1:length(method_data)){
        model <- hclust(d, method=method_data[i])
        # 各种谱系图画法
        # as.dendrogram()函数  ?as.dendrogram 查看帮助
        dend1 <- as.dendrogram(model)
        opar <- par(mfrow=c(2,2), mar=c(4,3,1,2))
        plot(dend1,cex=0.6)
        plot(dend1,nodePar=list(pch=c(1,NA), cex=0.8, lab.cex=0.8), type = "t", center=T)
        plot(dend1,edgePar=list(col=1:2,lty=2:3),dLeaf=1, edge.root = T)
        plot(dend1,nodePar=list(pch=2:1,cex=.4*2:1,col=2:3), horiz=T)
        par(opar)
    }
    par(opar)
    ##################################

图1.4：single方法进行聚类的各种谱系图画法示例

1.2.6) 美化聚类图形

    ##################################
    options(digits=4)
    mydata <- read.table("clipboard",header=T)
    class(mydata)
    dim(mydata)
    head(mydata)
    iris_model_data <- mydata[,2:4]
    d <- dist(iris_model_data, method="manhattan", diag = TRUE, upper = FALSE)
    hc <- hclust(d, method='single') 
    # 在此基础上，美化图形。
    op = par(bg = "grey")
    plot(hc, col="blue", col.main="black", col.lab="black", col.axis="black", lwd=1, lty=1, sub="", hang=-1, axes=FALSE)
    # add axis
    axis(side = 2, at = seq(0, 4, 1), col = "blue", labels = FALSE, lwd = 1)
    # add text in margin
    mtext(seq(0, 4, 1), side = 2, at = seq(0, 4, 1), line = 1, col = "blue", las = 2,outer = F)
    par(op)
    ##################################

图1.5：美化聚类图形

1.2.7) 分割系统树

    ##################################
    options(digits=4)
    mydata <- read.table("clipboard",header=T)
    class(mydata)
    dim(mydata)
    head(mydata)
    iris_model_data <- mydata[,2:4]
    d <- dist(iris_model_data, method="manhattan", diag = TRUE, upper = FALSE)
    hc <- hclust(d, method='single') 
    
    # 当然我们还可以使用系统树对象！
    hcd <- as.dendrogram(hc)
    # 绘制图形
    op <- par(mfrow = c(3, 1))
    plot(hcd)
    plot(hcd, type = "triangle")
    plot(hcd, type = "rectangle")
    # 我们还可以分割系统树
    # par(mfrow = c(1, 1))
    op <- par(mfrow = c(3, 1))
    # 一共分为2组
    plot(cut(hcd, h=2)$upper, main="Upper tree of cut at h=2")
    # 绘制第一、二组
    plot(cut(hcd, h=2)$lower[[1]], main="First branch of lower tree with cut at h=2")
    plot(cut(hcd, h=2)$lower[[2]], main="Second branch of lower tree with cut at h=2")
    par(op)
    
    # 分支合并
    # 我们可不可以将2组里面的分支部分合并呢？
    result<-cut(hcd, h=2)
    # 将1和2组合并
    result1<-merge(result$lower[[1]],result$lower[[2]])
    plot(result1)
    ##################################

图1.6：系统树图

图1.7：分割系统树图

1.2.8) 分组结果用颜色区分

    ##################################
    options(digits=4)
    mydata <- read.table("clipboard",header=T)
    class(mydata)
    dim(mydata)
    head(mydata)
    iris_model_data <- mydata[,2:4]
    d <- dist(iris_model_data, method="manhattan", diag = TRUE, upper = FALSE)
    hc <- hclust(d, method='single') 
    
    # 当然我们还可以使用系统树对象！
    hcd <- as.dendrogram(hc)
    
    # 我们还可以将分组结果用颜色区分出来
    library(RColorBrewer)
    labelColors <- brewer.pal(n=3, name="Set1")
    # 聚类分组
    clusMember <- cutree(hc, 3)
    ## 自定义函数
    ## toy example to set colored leaf labels :
    local({
      colLab <<- function(n) {
        if(is.leaf(n)) {
          a <- attributes(n)
          i <<- i+1
          attr(n, "nodePar") <-
            c(a$nodePar, list(lab.col = mycols[i], lab.font = i%%3))
        }
        n
      }
      mycols <- grDevices::rainbow(attr(hcd,"members"))
      i <- 0
    })
    clusDendro <- dendrapply(hcd, colLab)
    plot(clusDendro, main="Cool Dendrogram", type="triangle", horiz=T)
    plot(clusDendro, main="Cool Dendrogram", type="rectangle", horiz=T)
    ##################################

图1.8：triangle系统树图

图1.9：rectangle系统树图

1.2.9) 绘制比较有趣的图形

    ##################################
    options(digits=4)
    mydata <- read.table("clipboard",header=T)
    class(mydata)
    dim(mydata)
    head(mydata)
    iris_model_data <- mydata[,2:4]
    d <- dist(iris_model_data, method="manhattan", diag = TRUE, upper = FALSE)
    hc <- hclust(d, method='single') 
    
    # 其中，还有一个比较好用的包ape，可以绘制比较有趣的图形。
    library(ape)
    
    op <- par(mfrow = c(3, 2))
    # plot basic tree
    plot(as.phylo(hc), cex = 0.9, label.offset = 1)
    # cladogram
    plot(as.phylo(hc), type = "cladogram", cex = 0.9, label.offset = 1)
    # unrooted
    plot(as.phylo(hc), type = "unrooted",no.margin = T,cex = 0.5)
    # fan
    plot(as.phylo(hc), type = "fan")
    # radial
    plot(as.phylo(hc), type = "radial")
    # 我们还可以添加颜色。
    plot(as.phylo(hc),type = "fan",tip.color = hsv(runif(15, 0.65, 0.95), 1, 1, 0.7), edge.color = hsv(runif(10, 0.65, 0.75), 1, 1, 0.7), 
         edge.width = runif(20, 0.5, 3), use.edge.length = TRUE, 
         col = "gray80",cex=0.5)
    par(op)
    
    mycol <- c("#556270", "#4ECDC4", "#1B676B", "#FF6B6B", "#C44D58")
    clus5 <- cutree(hc, 5)
    op <- par(bg = "#1B676B")   # "#E8DDCB" 白色
    plot(as.phylo(hc), type = "fan", tip.color = mycol[clus5], label.offset = 1, cex = 0.7)
    par(op)
    ##################################

图1.10：趣图

图1.11： 添加背景色图

1.2.10) 使用包sparcl绘制聚类结果

    ##################################
    options(digits=4)
    mydata <- read.table("clipboard",header=T)
    class(mydata)
    dim(mydata)
    head(mydata)
    iris_model_data <- mydata[,2:4]
    d <- dist(iris_model_data, method="manhattan", diag = TRUE, upper = FALSE)
    hc <- hclust(d, method='single') 
    
    # 包sparcl也是可以绘制聚类结果的
    library(sparcl)
    y <- cutree(hc, 3)
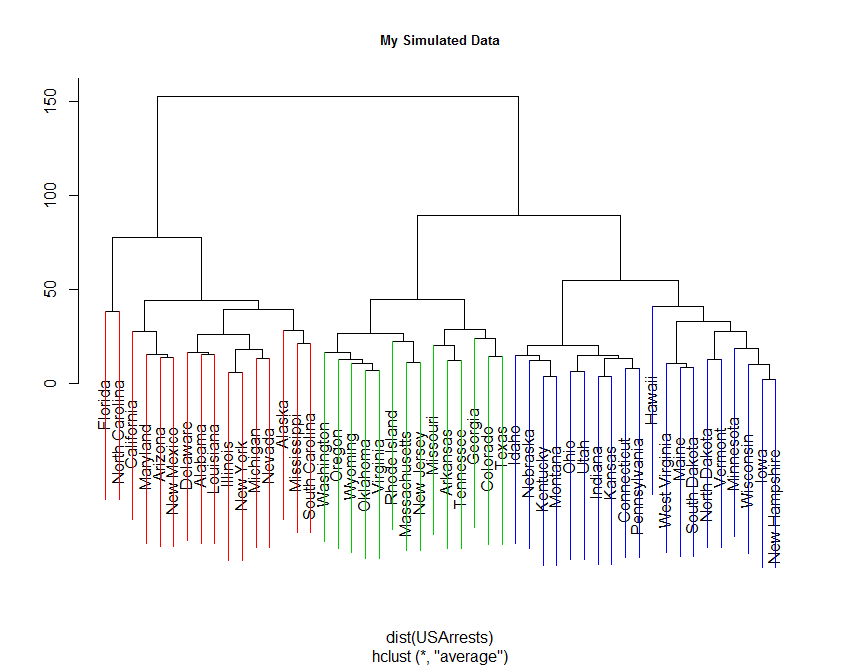
    ColorDendrogram(hc, y = y, labels = names(y), main = "My Simulated Data", cex=0.8, branchlength = 100)
    ##################################

图1.12： 包sparcl聚类结果图

1.2.11) 使用包ggdendro绘制聚类结果

    ##################################
    options(digits=4)
    mydata <- read.table("clipboard",header=T)
    class(mydata)
    dim(mydata)
    head(mydata)
    iris_model_data <- mydata[,2:4]
    d <- dist(iris_model_data, method="manhattan", diag = TRUE, upper = FALSE)
    hc <- hclust(d, method='single') 
    
    # 当然了，你还可以试试这个包ggdendro
    library(ggdendro)
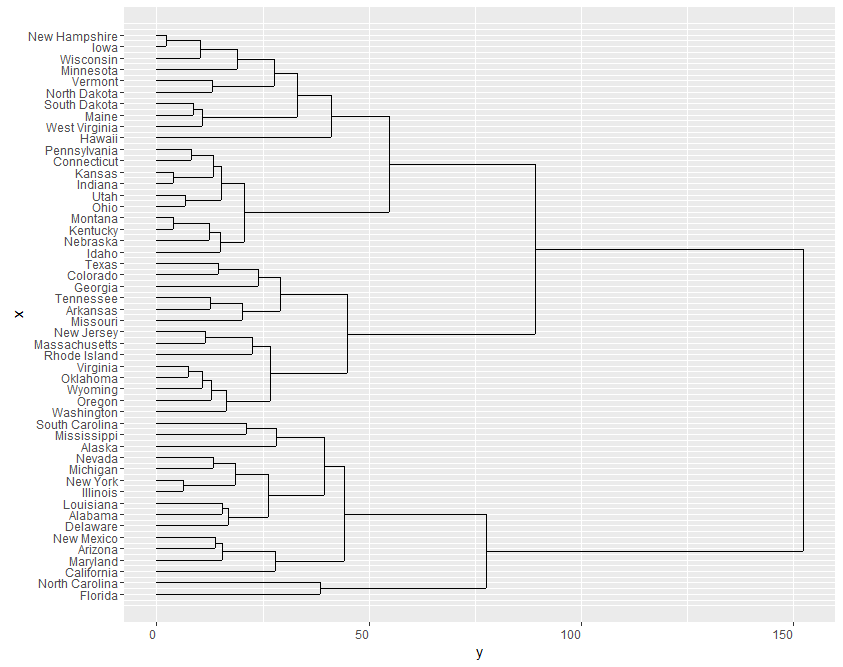
    ggdendrogram(hc)
    ggdendrogram(hc, rotate = TRUE,size = 1,theme_dendro = FALSE,color = "tomato")
    ddata <- dendro_data(as.dendrogram(hc), type = "triangle")
    ##################################

图1.13： 包ggdendro聚类结果图

---

2)Python实战

---

---

3)R语言函数总结

---

---

4)Python函数总结

---

---

转载于:https://www.cnblogs.com/cloudtj/articles/6793158.html