使用jupyter做数据分析与挖掘

使用jupyter做数据分析与挖掘

数据关系

统计量分析

1. describe
   describe会返回一系列参数，count，mean，std，min，25%，50%，75%，max。

describe()返回值的解释如下：

count：返回数组的个数，如上述为4个元素，所以返回为4；
mean：返回数组的平均值，1 3 5 9的平均值为4.5；
std：返回数组的标准差；
min：返回数组的最小值；
25%，50%，75%：返回数组的三个不同百分位置的数值，也就是统计学中的四分位数，其中50%对应的是中位数。
max：返回列表的最大值。

#统计量分析
#既最简单的标准差，数量，平均值，范围，变异系数（标准差/平均值）等数值的计算
from __future__ import print_function #用于代码兼容
import pandas as pd #pandas导入pandas库
rates = 'C:/Users/Kst/Downloads/皮马人糖尿病数据集(UCI) .xls' #输入数据所在位置
data = pd.read_excel(rates) #读取数据
statistics = data.describe() #保存基本统计量
statistics.loc['range'] = statistics.loc['max']-statistics.loc['min']#极差
statistics.loc['var'] = statistics.loc['std']/statistics.loc['mean']#变异系数
statistics.loc['dis'] = statistics.loc['75%']-statistics.loc['25%']#四分位数间距
print(statistics) 

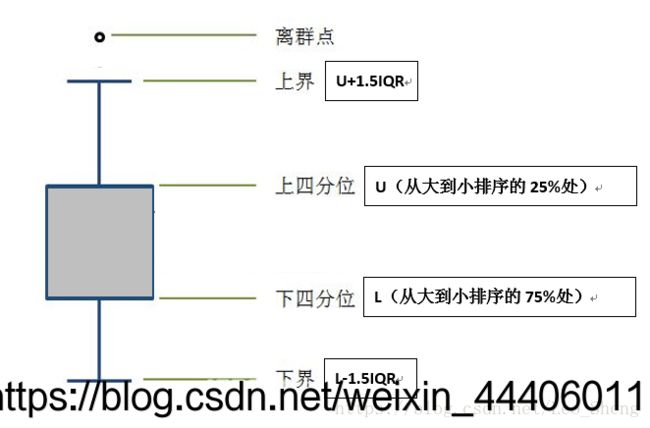
异常值分析

1. 箱型图原理
   箱型图通过程序设置一个识别异常值的标准，即大于或小于箱型图设定的上下界的数值则识别为异常值

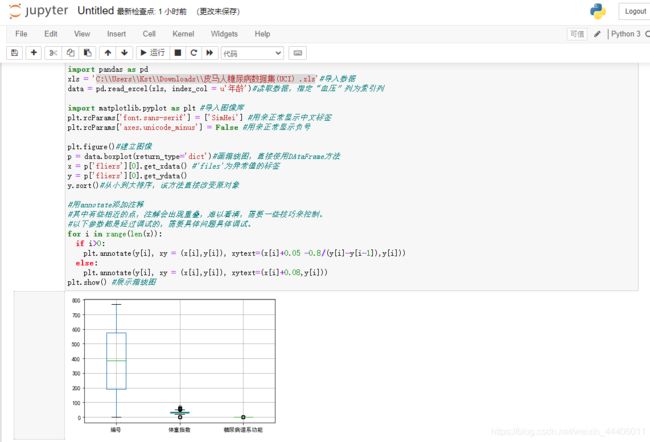
#异常值分析，即数据中存在不合理数据时需要进行剔除，也就是箱模型上下界的数据
import pandas as pd
xls = 'C:\\Users\\Kst\\Downloads\\皮马人糖尿病数据集(UCI) .xls'#导入数据
data = pd.read_excel(xls, index_col = u'年龄')#读取数据，指定“血压”列为索引列

import matplotlib.pyplot as plt #导入图像库
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号

plt.figure()#建立图像
p = data.boxplot(return_type='dict')#画箱线图，直接使用DAtaFrame方法
x = p['fliers'][0].get_xdata() #'files'为异常值的标签
y = p['fliers'][0].get_ydata()
y.sort()#从小到大排序，该方法直接改变原对象

#用annotate添加注释
#其中有些相近的点，注解会出现重叠，难以看清，需要一些技巧来控制。
#以下参数都是经过调试的，需要具体问题具体调试。
for i in range(len(x)):
  if i>0:
    plt.annotate(y[i], xy = (x[i],y[i]), xytext=(x[i]+0.05 -0.8/(y[i]-y[i-1]),y[i]))
  else:
    plt.annotate(y[i], xy = (x[i],y[i]), xytext=(x[i]+0.08,y[i]))
plt.show() #展示箱线图

贡献度分析

#贡献度分析
#贡献度分析又称为帕累托分析，2/8定律。
#例如：对一个公司来讲，80%的利率来自于20%的最畅销产品，其他80%只产生20%的利润，如某个餐厅不同菜品的盈利贡献
#-*- coding: utf-8 -*-
#盈利数据 帕累托图
from __future__ import print_function
import pandas as pd

#初始化参数
dish_profit ='C:\\Users\\Kst\\Downloads\\皮马人糖尿病数据集(UCI) .xls' #数据
data = pd.read_excel(dish_profit, index_col = u'年龄')
data = data[u'体重指数'].copy()
#data.sort_index(ascending = False)

import matplotlib.pyplot as plt #导入图像库
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号

plt.figure()
data.plot(kind='bar')
plt.ylabel(u'体重指数')
p = 1.0*data.cumsum()/data.sum()
p.plot(color = 'r', secondary_y = True, style = '-o',linewidth = 2)
plt.annotate(format(p[6], '.4%'), xy = (6, p[6]), xytext=(6*0.9, p[6]*0.9), arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2")) #添加注释，即85%处的标记。这里包括了指定箭头样式。
plt.ylabel(u'体重指数')
plt.show()

相关性分析

pearson:

相关性最主要的指标就是r

r<=0.3 不存在线性相关

0.3

r>0.8为高度线性相关

spearman秩相关：

两个变量具有严格单调的函数关系，就完全spearman相关，用r2表示，0<=r2<=1.

三个相关性系数==（pearson, spearman, kendall）==反应的都是两个变量之间变化趋势的方向以及程度，其值范围为-1到+1，0表示两个变量不相关，正值表示正相关，负值表示负相关，值越大表示相关性越强。

#餐饮销量数据相关性分析
from __future__ import print_function
import pandas as pd

catering_sale = '../data/catering_sale_all.xls' #餐饮数据，含有其他属性
data = pd.read_excel(catering_sale, index_col = u'日期') #读取数据，指定“日期”列为索引列

data.corr() #相关系数矩阵，即给出了任意两款菜式之间的相关系数
data.corr()[u'百合酱蒸凤爪'] #只显示“百合酱蒸凤爪”与其他菜式的相关系数
data[u'百合酱蒸凤爪'].corr(data[u'翡翠蒸香茜饺']) #计算“百合酱蒸凤爪”与“翡翠蒸香茜饺”的相关系数

import numpy as np
import pandas as pd
from scipy.stats import spearmanr



xls = 'C:\\Users\\Kst\\Downloads\\皮马人糖尿病数据集(wm) .xls'
data = pd.read_excel(xls,sheet_name='Sheet1')
data1 = pd.DataFrame(data)#DataFrame函数将excel中的数据转换为数据框结构



data2 = data1[[u'血压',u'年龄']]
data2.corr(method='spearman')

将数据缺失值进行插补

拉格朗日插值法

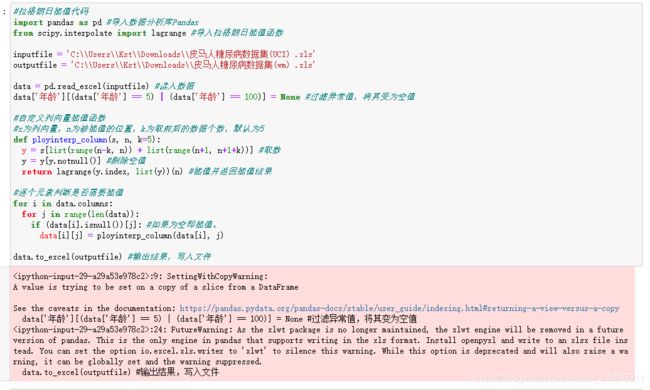
#拉格朗日插值代码
import pandas as pd #导入数据分析库Pandas
from scipy.interpolate import lagrange #导入拉格朗日插值函数

inputfile = 'C:\\Users\\Kst\\Downloads\\皮马人糖尿病数据集(UCI) .xls'
outputfile = 'C:\\Users\\Kst\\Downloads\\皮马人糖尿病数据集(wm) .xls'

data = pd.read_excel(inputfile) #读入数据
data['年龄'][(data['年龄'] == 5) | (data['年龄'] == 100)] = None #过滤异常值，将其变为空值

#自定义列向量插值函数
#s为列向量，n为被插值的位置，k为取前后的数据个数，默认为5
def ployinterp_column(s, n, k=5):
  y = s[list(range(n-k, n)) + list(range(n+1, n+1+k))] #取数
  y = y[y.notnull()] #剔除空值
  return lagrange(y.index, list(y))(n) #插值并返回插值结果

#逐个元素判断是否需要插值
for i in data.columns:
  for j in range(len(data)):
    if (data[i].isnull())[j]: #如果为空即插值。
      data[i][j] = ployinterp_column(data[i], j)

data.to_excel(outputfile) #输出结果，写入文件

数据规范化

将数据按照比例进行缩放，是之落到一个特定的区域，如工资映射到[-1,1]或者[0,1]

（1）最小-最大规范化：离查差标准化

公式如下：x*= x-min/max-min

（2）零-均值规范化:标准差标准化

x*=x-x(平均值）/σ

是使用最多的数据标准化的方法

（3）小数定标志规范化
x=x/10**k

取决于属性绝对值的最大值

#数据规范化
import pandas as pd
import numpy as np

datafile = 'C:\\Users\\Kst\\Downloads\\皮马人糖尿病数据集(UCI) .xls' #参数初始化
data = pd.read_excel(datafile, header = None) #读取数据

print((data - data.min())/(data.max() - data.min())) #最小-最大规范化
print((data - data.mean())/data.std()) #零-均值规范化
print(data/10**np.ceil(np.log10(data.abs().max()))) #小数定标规范化

连续属性离散化

#-*- coding: utf-8 -*-
#数据规范化
import pandas as pd

datafile = 'C:\\Users\\Kst\\Downloads\\皮马人糖尿病数据集(UCI) .xls' #参数初始化
data = pd.read_excel(datafile) #读取数据
data = data[u'糖尿病谱系功能'].copy()
k = 4

d1 = pd.cut(data, k, labels = range(k)) #等宽离散化，各个类比依次命名为0,1,2,3

#等频率离散化
w = [1.0*i/k for i in range(k+1)]
w = data.describe(percentiles = w)[4:4+k+1] #使用describe函数自动计算分位数
w[0] = w[0]*(1-1e-10)
d2 = pd.cut(data, w, labels = range(k))

#一维聚类
from sklearn.cluster import KMeans #引入KMeans
kmodel = KMeans(n_clusters = k, n_jobs = 4) #建立模型，n_jobs是并行数，一般等于CPU数较好
kmodel.fit(data.values.reshape((len(data), 1))) #训练模型
c = pd.DataFrame(kmodel.cluster_centers_).sort_values(0) #输出聚类中心，并且排序（默认是随机序的）
w = c.rolling(2).mean().iloc[1:]#相比两项求中点，作为边界线
w = [0] + list(w[0]) + [data.max()] #把首末边界点加上
d3 = pd.cut(data, w, labels = range(k))

def cluster_plot(d, k): #自定义作图函数来显示聚类结果
  import matplotlib.pyplot as plt
  plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
  plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
  
  plt.figure(figsize = (8, 3))
  for j in range(0, k):
    plt.plot(data[d==j], [j for i in d[d==j]], 'o')
  
  plt.ylim(-0.5, k-0.5)
  return plt

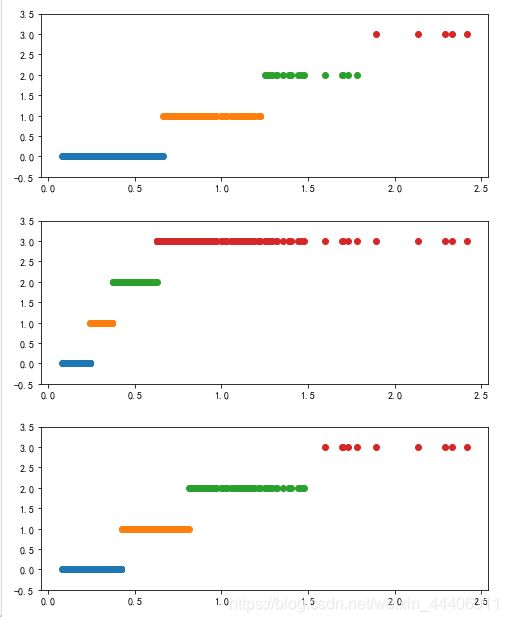
cluster_plot(d1, k).show()

cluster_plot(d2, k).show()
cluster_plot(d3, k).show()

1. 等宽法 ：将属性的值域分为具有相同宽度的区间
2. 等频法：将相同数量的记录放进每个区间
3. 基于k-means一维聚类
   

属性构造

即利用已有的属性构造新的属性

#折损率构造
import pandas as pd

#参数初始化
#文件输入路径
inputfile = "C:\\Users\\Kst\\Downloads\\皮马人糖尿病数据集(UCI) .xls" 
#文件输出路径
outputfile = "C:\\Users\\Kst\\Downloads\\皮马人糖尿病数据集(wmm) .xls"
# 读取数据
data = pd.read_excel(inputfile)
data[u'折损'] = data[u'胰岛素']

data.to_excel(outputfile,index = False)

https://zhuanlan.zhihu.com/p/57987720