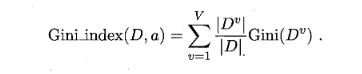决策树分类算法
1.算法概要
决策树是一种树形结构的分类算法,利用递归的思想不断进行划分。从训练数据中学习一个类似于流程图的树形结构。其中每个内部结点表示一种属性的判断,每个分支(将样本根据属性值划分成多个相应分支的样本子集)表示判别结果的输出,每个叶节点表示一种分类结果。下面上一个图:
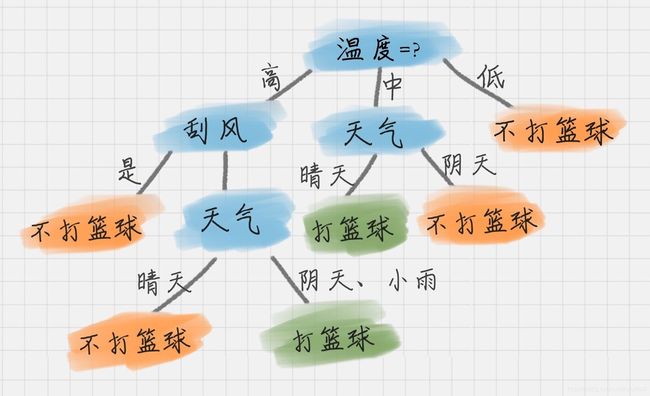
图中表达地非常清楚,通过一步步的判断、划分,最终得到类别。
这时有两个比较重要的问题出现了:
- 如何确定先选哪个属性进行判断、划分
- 什么时候就停止属性的判断、划分呢。注意!如果都进行判断、划分将会导致模型过拟合,所以要剪枝挑选
2.重点分析
1.属性划分选择
我们先了解如下几个概念
- 信息量,符号表示为h,h(x)代表随机事件发生这件事包含多少信息量,h(x) = -log p(x) (其中p(x)表示事件x发生的概率)
- 熵,物理和化学中的概念,代表一个系统的混乱程度,熵越大,混乱程度越大
- 信息熵,符号表示为H, H(x)代表各种x所有可能取值的信息量的期望(可以粗糙地理解为信息量的平均值,实际为加权平均),假定当前样本集合D中第k类样本所占的比例为pk(k = 1,2,. . . , |Y|),则D的信息熵是
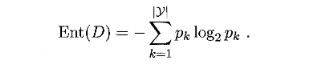
信息熵用来衡量事件的确定程度,信息熵越大代表事件的可能性越多,越不确定,比如明天下雨和晴天的概率均为0.5,也就是不确定性最大的情况,这时信息熵为log2;当明天下雨的概率为1时,确定性最大,信息熵为0。在决策树划分的时候,我们希望分支节点样本尽可能属于同一类,即节点的“纯度越高越好”,而Ent(D)越小,说明不确定性越低,纯度越高。
下面开始介绍三种属性划分的方法
-
ID3算法,以信息增益为准则。信息增益:随机变量y的信息熵减去考虑随机变量x的y的条件熵,衡量在考虑随机变量x的情况下y的不确定性减少的程度。可以知道信息增益越大,考虑随机变量x的情况下y的不确定性减少的程度越大,这个x就是我们要的,即 信息增益最大的属性做为最优划分属性
假定离散属性a有V个可能的取值{a1,a2,…,aV}考虑a属性来对样本集D进行划分,则会产生V个分支结点,中第v个分支结点包含了D中所有在属性a上取值为av的样本记为Dv.先上个信息增益公式
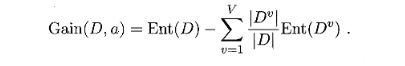
计算出DV的信息熵累加,再考虑到不同的分支结点所包含的样本数不同,给分支结点赋予权重|DV| / |D|,实际就是在求期望。按照这样求出每个属性的信息增益,最大的属性选为最优划分属性 -
C4.5算法,这个方法是为了解决ID3算法对取值数目较多的属性有所偏好的问题,这里的度量是增益率,先上公式,增益率:
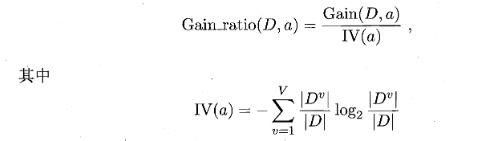
实际上就是在ID3的公式里除了一个与属性数目成正比的值,进而削弱偏好影响。同样将增益率最大的属性作为最优划分属性。天下没有免费的午餐,C4.5算法对取值数目较少的属性有所偏好,所以,一般先用ID3计算出信息增益取最大的前几个属性,再用C4.5得到最大增益率的属性。 -
CART算法基尼系数(Gini),Gini(D)反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率.因此,Gini(D)越小,则数据集D的纯度越高,将Gini(D)最小的属性作为划分属性
2.停止条件
递归停止设为叶节点条件:
- 当节点样本label一样,
- 当节点样本属性值一样或已经没有特征,(每次对一个属性A进行划分后,产生的每个分支中属性A整列都会被删除)label按照父节点样本最多的label
- 当节点分支子集没有样本,label按照节点样本最多的label
3.剪枝处理防止过拟合
将数据集分为训练集和测试集
-
预剪枝,树生成的过程中进行处理
开始根节点有所有的样本,先不划分根节点此时设为了叶节点,类别占比样本数最高的判为最终类别,利用这个结果进行测试集预测得到准确率;再进行划分,得到此时的准确率。若前者小于后者,则节点进行划分;反之,将停止划分,将这个节点设为叶节点,定这个节点的类别,即所谓的剪枝。从上而下,每个节点都递归的进行剪枝。预剪枝可以一定程度上减少时间的开销,但有欠拟合的风险,有些划分当前泛化能力不好,但之后可能有很大的提升。
-
后剪枝,树生成后进行
从下而上,对于每个含有叶节点的节点,计算当前这棵树的预测准确率a1;和把当前要考虑的节点的叶节点分支收回计算预测准确率a2。a1
关于剪枝,周志华的西瓜书有具体的例子,有兴趣的可以去看看。
3.优缺点
优点:计算量简单,可解释性强,多分类,能够处理不相关的特征
缺点:容易过拟合,导致泛化能力弱
4.代码实现
下面是C4.5算法
导入包
import numpy as np
计算信息熵,为了方便这里的dataset还包含了标签,
def calcShannonEnt(dataSet):
total = len(dataSet)
labelCounts = {}#利用字典记录每个类别样本个数
for featVec in dataSet:
Labels = featVec[-1]#取每个样本的label
if Labels not in labelCounts.keys():
labelCounts[Labels]=0
labelCounts[Labels] +=1
shannonEnt = 0.0
for key in labelCounts:
#Prob代表该标签类出现的概率,为该标签出现次数/总次数
prob = float(labelCounts[key])/total
shannonEnt -= prob*np.log2(prob)
return shannonEnt
数据集分割,得到特征feature取值为value的子集,返回之前还要将子集中feature特征项
删除
def splitDataSet(dataSet,feature,value):
retDataSet = []
for featVec in dataSet:
#判断特征值是否与给定值匹配
if featVec[feature] == value:
#将对应的特征项挖去
reducedFeatVec = featVec[:feature]
reducedFeatVec.extend(featVec[feature+1:])#将剩下的数据一个一个加到list中
retDataSet.append(reducedFeatVec)#将去掉对应特征项的数据加入
return retDataSet
计算信息增益得到最佳划分方式
def featureToSplit_ID3(dataSet):
total = len(dataSet[0])-1 #特征数
entropy = calcShannonEnt(dataSet)#得到初始乡农熵
bestInfoGain = 0.0#初始信息熵
bestFeature = -1#初始特征
for i in range(total):
featList = [x[i] for x in dataSet]#得到每一个特征的特征值列表
uniqueVals = set(featList)#得到特征值列表的集合
newEntropy = 0.0
#遍历特征值集合
for value in uniqueVals:
subDataSet = splitDataSet(dataSet,i,value)#得到符合该特征值的数据集
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob*calcShannonEnt(subDataSet)
infoGain = entropy - newEntropy
#得到所有特征中香农熵最小的特征对应的索引
if(infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature#返回索引
计算增益率得到最佳划分方式,相比上面的ID3,只是多了一步求IV
#k指的是先取信息增益前k个大的特征, 再进行k个特征的增益率比较
def featureToSplit_C4_5(dataSet,k=3):
total = len(dataSet[0])-1
entropy = calcShannonEnt(dataSet)
InfoGain = []
IV = []
for i in range(total):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0.0
Iv = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet,i,value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob*calcShannonEnt(subDataSet)
Iv += -prob*np.log2(prob)
Gain = entropy - newEntropy
InfoGain.append(Gain)
IV.append(Iv)
n = []
Gain = InfoGain.copy()#进行深拷贝 防止数据丢失
for j in range(k):
indexs = Gain.index(max(Gain))
Gain.remove(max(Gain))
n.append(indexs)
Feature = [InfoGain[i]/IV[i] for i in n]
bestFeature = n[Feature.index(min(Feature))
return bestFeature#返回索引
再叶节点时进行投票选出类别
def majorityCnt(classList):
classCount = {}
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] +=1
sortedClassCount = max(classCount,key=classCount.get)
return sortedClassCount
创建树,最终以字典的形式储存树
def createTree(dataSet,labels):
#类别
classList = [x[-1] for x in dataSet]
#**第一个终止条件:所有的类别标签相同
if classList.count(classList[0]) == len(classList):
return classList[0]
#**第二个终止条件:消耗了所有特征后,所有类别标签不尽相同,需要投票表决
if len(dataSet[0]) == 1 :
return majorityCnt(classList)
#得到当前数据集的最优划分的特征索引值
bestFeat = featureToSplit_ID3(dataSet)
bestFeatLabel = labels[bestFeat]
#构建树的分支字典,索引代表分支的判断条件
myTree = {bestFeatLabel:{}}
#从特征列表中去除已经消耗的特征项
del(labels[bestFeat])
#得到数据集中当前最优特征的所有特征值的集合
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
#**第三个终止条件:该特征的值都相等
if len(uniqueVals)==1:
return majorityCnt(classList)
#遍历特征值,不同特征值代表当前节点的不同分支
for value in uniqueVals:
subLabels = labels.copy() #深拷贝 防止改变原列表
cdataSet = splitDataSet(dataSet,bestFeat,value)
#**第四个终止条件:子集为空时
if cdataSet :
myTree[bestFeatLabel][value] = createTree(cdataSet,subLabels)
else:
majorityCnt(classList)
#返回的值插入到上一层的树字典中
return myTree
预测,输入一个样本
def predict(inTree,featLabels,testVec):
firstStr = list(inTree.keys())[0]
secondDict = inTree[firstStr]
featIndex = featLabels.index(firstStr)
key = testVec[featIndex]
valueOfFeat = secondDict[key]
if isinstance(valueOfFeat,dict):
classLabel = classify(valueOfFeat,featLabels,testVec)
else:
classLabel = valueOfFeat
return classLabel
#构建几个简单的数据进行测试
dataSet = [[0,0,0,0,'N'],
[0,0,0,1,'N'],
[1,0,0,0,'Y'],
[2,1,0,0,'Y'],
[2,2,1,0,'Y'],
[2,2,1,1,'N'],
[1,2,1,1,'Y']]
labels = ['otlook', 'temperature', 'humidicy', 'windy']
testSet = [[0,1,0,0],
[0,2,1,0],
[2,1,1,0],
[0,1,1,1],
[1,1,0,1],
[1,0,1,0],
[2,1,0,1]]
a = labels.copy()#深拷贝 labels要进行递归调用 防止改变原列表
tree = createTree(dataSet,labels)
print(tree)
pre = predict(tree,a,(1,0,0,0))
print(pre)
pre = predict(tree,a,[1,2,1,1])
print(pre)
pre = predict(tree,a,[0,0,0,0 ])
print(pre)
{'otlook': {0: 'N', 1: 'Y', 2: {'windy': {0: 'Y', 1: 'N'}}}}
Y
Y
N
5.小结
这里没有进行剪枝处理,还有没有提到特征值是连续值的问题以及如何处理