【1】深度神经网络的前向/反向传播算法

1.感知机

1.1 基本介绍

        神经网络的发展，最早可以追溯到感知机模型，我们不妨理解为当前的神经网络模型，都是从感知机进化而来的，因此，在正式学习神经网络之前，认识一下它的“祖先”还是很有必要的。
                       
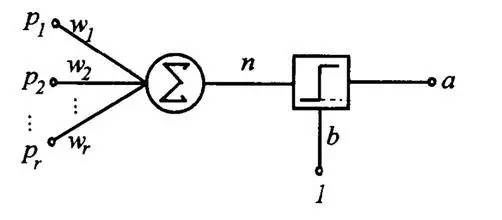
        上图就是对感知机的完整诠释，这个名字有点误导，因为它根本上就是做决策用的。

       举个例子:
       你正在考虑今天要不要出去看电影，你主要考虑的有三个因素p₁ 、p₂和p₃。其中p₁是你女朋友想不想去，p₂是电影好不好看，p₃是今天工作多不多，每一个因素对应于一个权重w_i，有的人看重女朋友，有的人看重电影的质量…
       你把每一项p_i和对应的w_i相乘，然后累加求和得到一个结果，如果这个值大于设定的阈值，那么你就决定去看电影，如果小于等于设定的阈值，那么就不去看，这就是感知机做决策的例子。

1.2 感知机模型

        根据上面的叙述，我们大概知道，感知机的决策过程主要分两步，一是计算输入乘以权重的累加和，二是判断累加和与阈值之间的大小关系。我们可以把两个步骤合并在一起，把阈值b与累加和相加，再用$sign(x)$函数得到输入结果。
        我们先计算累加和与bias项的和：$$z=\sum _{i=1}^m{w}_i{x}_i+b$$        得到中间结果$z$之后，我们可以再用激活函数$sign(x)$，得到最终的决策值：
$$\mathrm{sign}(z)=\{\begin{array}{ll}-1& z<0\\ 1& z\ge 0\end{array}$$

1.3 逻辑回归

        不知道大家有没有和我一样的感受，看了感知机的原理之后，就想到了逻辑回归模型，因为二者的相似处实在太多，想想逻辑回归也是计算特征值的加权和，然后喂给了$Sigmoid$激活函数，得到最终的输出结果。

        从函数的判别模型角度来看，感知机和逻辑回归还是挺相似的，那么逻辑回归模型，是否也可以像感知机一样，理解为只含有一个神经元的神经网络模型呢？同理，由LogisicRegression拓展到多分类任务的SoftmaxRegression，是否也是一种特殊的神经网络呢？

        这个只是我目前的学习思考，之后学习的更深之后，再来解答此问题，不容否认的是，逻辑回归和神经网络之间一定是有着某种特别的联系的。

1.4 感知机到神经网络的演化

        上述的感知机模型，只能用于线性的二分类任务，无法用于复杂的非线性多分类任务，于是在此基础上进行一些扩展，得到了现在我们熟知的神经网络，主要有三点扩展：

1. 增加了隐藏层，提升了模型的表达能力，隐藏层的层数以及每层神经元的个数需要自己设计，代价是增加了模型的复杂程度，计算量增加；
2. 增加了输出层的神经元个数，有1个变为多个，带来的好处是可用于多分类任务、或其他机器学习领域如降维和聚类；
3. 增加了激活函数的种类，感知机的激活函数是$sign(z)$，虽然简单但是能力有限，常用的激活函数有$Sigmoid、ReLU、tanh和softmax$等，这里有详细介绍不同激活函数的区别和优缺点。

2.深度神经网络DNN

2.1 基本概念

        深度神经网络，也被叫做多层神经网络，偶尔也会被叫做多层感知机模型（Multi-Layer perceptron , MLP），我们只需要知道它们指的都是同一个东西即可，这里我们统称为DNN.

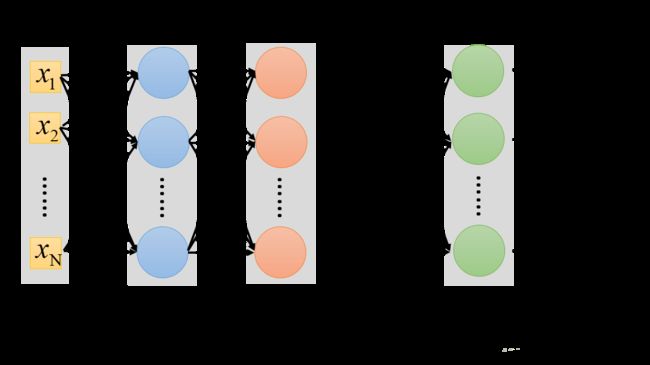
        深度神经网络的架构图如下：
                
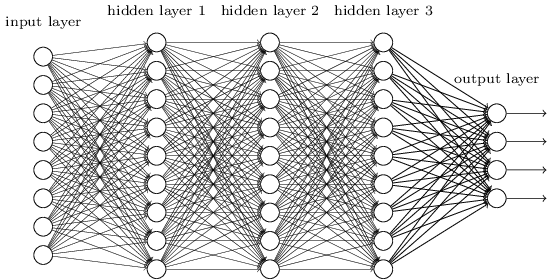
        层与层之间是全连接的，即第(l-1)层的任意一个神经元一定与第l层的任意一个神经元相连接。DNN的结构看起来是很复杂，但是我们单独抽出某一个神经元以及它上一层中的所有神经元，就会发现它其实就是和感知机（还是说逻辑回归？）一样，首先是计算加权和，再加上偏置项b，最终将这个未激活值送到激活函数σ进行激活。

2.2 符号定义

        $w_{42}^3:$ 表示第(3-1)层的第2个神经元到第3层的第4个神经元之间的连接的权重；

        $z_4^3:$   表示第3层的第4个神经元的未经激活函数激活之前的值，其中$$z_4^3=w_{41}^3\cdot a_1^2+w_{42}^3\cdot a_2^2+w_{43}^3\cdot a_3^2+b_4^3$$        $a_3^4:$   表示第3层的第4个神经元的激活值（输出值），其中
$$a_4^3=\sigma \left(z_4^3\right)$$        $b_4^3:$   表示第3层的第4个神经元所对应的偏置项，注意哦，每一层的每一个神经元都对应着一个b，我们把每一个神经元看成是一个感知机模型，所以每个模型对应的bias项是不一样的；

【引申一个问题】为什么要在未激活值的计算中加上bias项呢？这里引用知乎上的回答。

回答一：我们可以把问题先简化，为什么线性模型要加 bias？答案很简单，不加 bias 你的分类线(面)就必须过原点，这显然是不灵活的。有了bias我们就可以上下左右移动我们的线了，神经网络是一样的道理。

回答二：Bias的好处在于：可以使得神经网络Fit的范围得到左右的调整。
                
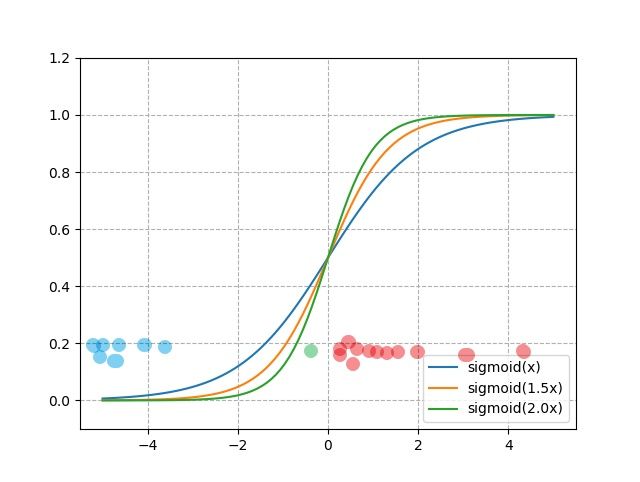
       没有bias项时，我们用不同的w来拟合数据，w越大，sigmoid函数越陡峭，分类效果越好！！可观察上图。但是如果要判断图中绿色点的类别呢？按照sigmoid函数的输出，绿色点的激活值小于0.5,应该判为蓝色类，这个时候，让sigmoid函数变得更陡也没办法解决了。
       这个时候，如果加入一个bias项呢？我们观察函数图像：
         
       w系数不需要学的很大，就可以提高学习的准确率，网络就能够非常灵活的拟合样本点的分布，并准确判断绿点所属的集合。
       简单来说，加上bias项能够更加灵活的fit数据样本点的分布！

2.3 DNN的前向传播算法

        假设一个神经网络共有三层，第一层（输入层）共有三个神经元x₁,x₂,x₃，第二层也是有三个神经元，第三层为输出层，只有1个神经元。如下图所示：
                        
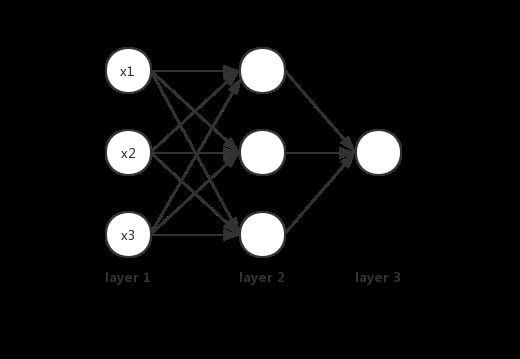
        那么第二层的三个神经元的输出分别为：$$\begin{array}{rl}{a}_1^2& =\sigma \left(z_1^2\right)=\sigma \left(w_{11}^2{x}_1+w_{12}^2{x}_2+w_{13}^2{x}_3+b_1^2\right)\\ & \\ a_2^2& =\sigma \left(z_2^2\right)=\sigma \left(w_{21}^2{x}_1+w_{22}^2{x}_2+w_{23}^2{x}_3+b_2^2\right)\\ & \\ a_3^2& =\sigma \left(z_3^2\right)=\sigma \left(w_{31}^2{x}_1+w_{32}^2{x}_2+w_{33}^2{x}_3+b_3^2\right)\end{array}$$        第三层的神经元输出为：$$a_1^3=\sigma \left(z_1^3\right)=\sigma \left(w_{11}^3{a}_1^2+w_{12}^3{a}_2^2+w_{13}^3{a}_3^2+b_1^3\right)$$        将上述例子一般化，假设第$(l-1)$层共有m个神经元，那么对于第l层的第j个神经元的输出值$a_j^l$为:$$a_j^l=\sigma (z_j^l)=\sigma (\sum _{k=1}^m{w}_{jk}^l{a}_k^{l-1}+b_j^l)$$

【矩阵法表示】上面这个式子，给出了单个神经元的输出值用代数法如何计算，我们下面来推导更加简洁的矩阵法表示.（最终结果如下：）
$$a^l=\sigma \left(z^l\right)=\sigma \left(W^l{a}^{l-1}+b^l\right)$$        假设第$(l-1)$层共有m个神经元，而第$l$层共有n个神经元，则第l层的权重系数w组成了一个n×m的矩阵$W^l$:$$\left(\begin{array}{llll}{w}_{11}^l& w_{12}^l& \dots & w_{1m}^l\\ & & & \\ w_{21}^l& w_{22}^l& \dots & w_{2m}^l\\ & & & \\ ...& ...& \dots & ...\\ & & & \\ w_{n1}^l& w_{n2}^l& \dots & w_{nm}^l\end{array}\right)$$        第$(l-1)$层的输出$a$组成了一个m×1的向量$a^{l-1}$：$$\left(\begin{array}{l}{a}_1^{l-1}\\ \\ a_2^{l-1}\\ \\ ...\\ \\ a_m^{l-1}\end{array}\right)$$        第$l$层的偏置向量$b$组成了一个n×1的向量$b^l$：$$\left(\begin{array}{l}{b}_1^l\\ \\ b_2^l\\ \\ ...\\ \\ b_n^l\end{array}\right)$$        整个过程可以用矩阵和向量进行表示：
$$\left(\begin{array}{l}{a}_1^l\\ \\ a_2^l\\ \\ ...\\ \\ a_n^l\end{array}\right)=\sigma \left(\left(\begin{array}{llll}{w}_{11}^l& w_{12}^l& \dots & w_{1m}^l\\ w_{21}^l& w_{22}^l& \dots & w_{2m}^l\\ ...& ...& \dots & ...\\ w_{n1}^l& w_{n2}^l& \dots & w_{nm}^l\end{array}\right)\left(\begin{array}{l}{a}_1^{l-1}\\ \\ a_2^{l-1}\\ \\ ...\\ \\ a_m^{l-1}\end{array}\right)+\left(\begin{array}{l}{b}_1^l\\ \\ b_2^l\\ \\ ...\\ \\ b_n^l\end{array}\right)\right)$$        用矩阵的形式表达，即为：
$$a^l=\sigma \left(z^l\right)=\sigma \left(W^l{a}^{l-1}+b^l\right)$$

2.4 前向传播算法小结

        DNN的前向传播算法也就是利用我们的若干个权重系数矩阵$W$，偏置向量$b$来和输入值向量$x$进行一系列线性运算和激活运算，从输入层开始，一层层的向后计算，一直到运算到输出层，得到输出结果为止。

2.5 DNN反向传播算法的基本思路

        首先我们要明白反向传播算法的定义：

对DNN的损失函数用梯度下降法进行迭代优化求极小值的过程即为我们的反向传播算法。

(此处之后的内容为 2019/6/25 更新 )

2.6 符号定义（重要！！！）

  为了使数学推导过程更加清晰简洁，我们定义符号表达如下：

• $L$  ——— 神经网络的总层数
• $n^l$ ——— 第$l$层神经元的总个数
• $w_{jk}^l$ ——— 第$l-1$层的第$k$个神经元到第$l$层的第$j$个神经元的连接权重
• $b_j^l$ ——— 第$l$层的第$j$个神经元的截距项 $bias$
• $W^l$ ——— 第$l$层神经元的权重系数矩阵（由$w_{jk}^l$构成的矩阵）
• $b^l$ ——— 第$l$层神经元的截距向量（由$b_j^l$构成的向量）
• $z_j^l$ ——— 第$l$层第$j$个神经元的加权输入
• $z^l$ ——— 第$l$层神经元的加权输入向量（由$z_j^l$构成的向量）
• $a_j^l$ ——— 第$l$层第$j$个神经元的激活函数输出值
• $a^l$ ——— 第$l$层神经元的激活函数输出向量（由$a_j^l$构成的向量）
• $C$ ——— 损失函数，$C=\frac{1}{n}{\sum }_x{C}_x$，其中$C_x$是每个独立训练样本的损失函数，反向传播针对单个训练数据计算偏导数用$\frac{\partial C_x}{\partial w}$ 和$\frac{\partial C_x}{\partial b}$，针对n个样本数据，计算偏导数，则用$\frac{\partial C}{\partial w}$ 和$\frac{\partial C}{\partial b}$
• $s\odot t$ ——— Hadamard积，表示两个维度相同的向量的对应元素(element-wise)相乘，例如：
  $$s\odot t=\left[\begin{array}{l}1\\ 2\end{array}\right]\odot \left[\begin{array}{l}3\\ 4\end{array}\right]=\left[\begin{array}{l}1\times 3\\ 2\times 4\end{array}\right]=\left[\begin{array}{l}3\\ 8\end{array}\right]$$

  根据神经网络的前向传播，有：

  对于$l=1$，即输入层，有：
$$z^1=a^1=x$$

  对于$l=2,3,4,...,L$，有：
$$z_j^l=\sum _{k=1}^{k=n^{l-1}}{w}_{jk}^l{a}_k^{l-1}+b_j^l$$

$$a_j^l=\sigma \left(z_j^l\right)$$
  向量化表达为：
$$\begin{array}{rl}{z}^l& =w^l{a}^{l-1}+b^l\\ & \\ a^l& =\sigma \left(z^l\right)\end{array}$$

  详细的矩阵表达为：
$$\left(\begin{array}{l}{a}_1^l\\ \\ a_2^l\\ \\ ...\\ \\ a_n^l\end{array}\right)=\sigma \left(\left(\begin{array}{llll}{w}_{11}^l& w_{12}^l& \dots & w_{1m}^l\\ w_{21}^l& w_{22}^l& \dots & w_{2m}^l\\ ...& ...& \dots & ...\\ w_{n1}^l& w_{n2}^l& \dots & w_{nm}^l\end{array}\right)\left(\begin{array}{l}{a}_1^{l-1}\\ \\ a_2^{l-1}\\ \\ ...\\ \\ a_m^{l-1}\end{array}\right)+\left(\begin{array}{l}{b}_1^l\\ \\ b_2^l\\ \\ ...\\ \\ b_n^l\end{array}\right)\right)$$

2.7 反向传播的四个基本等式

• $(1){\delta }^L=\frac{\partial C}{\partial z^L}={\nabla }_{a}C\odot {\sigma }^{\prime }\left(z^L\right)$

证明：
   取输出层的某一个神经元$a_j^L$为例，根据链式法则：
$${\delta }_j^L=\frac{\partial C}{\partial z_j^L}=\frac{\partial C}{\partial a_j^L}\cdot \frac{\partial a_j^L}{\partial z_j^L}$$

   取 ${\sigma }^{\prime }\left(z_j^L\right)=\frac{\partial a_j^L}{\partial z_j^L}$，可以得到：
$${\delta }_j^L=\frac{\partial C}{\partial a_j^L}{\sigma }^{\prime }\left(z_j^L\right)$$
   如果把输出层的所有神经元写成向量的形式，将${\left[\frac{\partial C}{\partial a_1^L},\frac{\partial C}{\partial a_2^L},\dots ,\frac{\partial C}{\partial a_m^L}\right]}^T$记为${\nabla }_{a}C$，将$[{\sigma }^{\prime }(z_1^L),{\sigma }^{\prime }(z_1^L),\dots ,{\sigma }^{\prime }(z_m^L){]}^T$记为${\sigma }^{\prime }\left(z_j^L\right)$，即可得到：

$${\delta }^L=\frac{\partial C}{\partial z^L}={\nabla }_{a}C\odot {\sigma }^{\prime }\left(z^L\right)$$

• $(2){\delta }^l=\left({\left(w^{l+1}\right)}^T{\delta }^{l+1}\right)\odot {\sigma }^{\prime }\left(z^l\right)$

证明：
   反向传播是从后往前计算的，因此我们在求解${\delta }^l$的时候，${\delta }^{l+1}$是作为已知量看待。于是根据链式法则可得：
$$\begin{array}{rl}{\delta }_j^l& =\frac{\partial C}{\partial z_j^l}\\ & =\sum _{k=1}^{n^{l+1}}\frac{\partial C}{\partial z_k^{l+1}}\frac{\partial z_k^{l+1}}{\partial z_j^l}\\ & =\sum _{k=1}^{n^{l+1}}\frac{\partial z_k^{l+1}}{\partial z_j^l}{\delta }_k^{l+1}\end{array}$$

   如下图所示，其中$n^{l+1}$指的是$l+1$层神经元的个数。

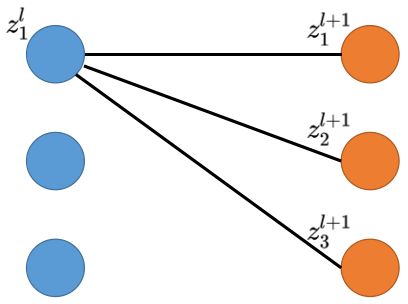
   另外，我们将$z_k^{l+1}$展开可得：
$$z_k^{l+1}=\sum _j^{n^l}{w}_{kj}^{l+1}{a}_j^l+b_k^{l+1}=\sum _j^{n^l}{w}_{kj}^{l+1}\sigma \left(z_j^l\right)+b_k^{l+1}$$

   于是，计算$\frac{\partial z_k^{l+1}}{\partial z_j^l}$的值为：
$$\frac{\partial z_k^{l+1}}{\partial z_j^l}=w_{kj}^{l+1}\cdot {\sigma }^{\prime }(z_j^l)$$

   如下图所示

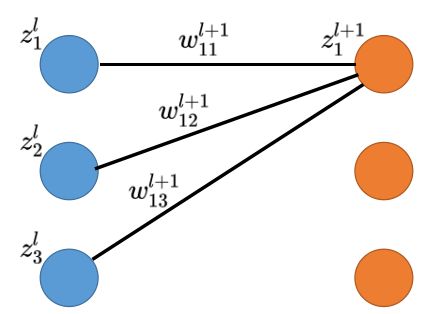
   代入到上面的${\delta }_j^l={\sum }_k^{n^{l+1}}\frac{\partial z_k^{l+1}}{\partial z_j^l}{\delta }_k^{l+1}$，可以得到：
$${\delta }_j^l=\sum _k^{n^{l+1}}{w}_{kj}^{l+1}{\delta }_k^{l+1}{\sigma }^{\prime }\left(z_j^l\right)$$

   如下图所示

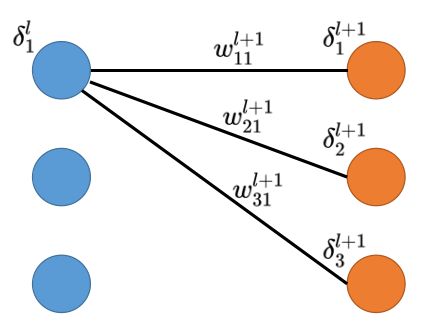
   上式向量化表达为：
$${\delta }_j^l=[w_{1j}^{l+1},w_{2j}^{l+1},\dots ,w_{n^{l+1}j}^{l+1}]\left[\begin{array}{c}{\delta }_1^{l+1}\\ {\delta }_2^{l+1}\\ \cdots \\ {\delta }_{n^{l+1}}^{l+1}\end{array}\right]{\sigma }^{\prime }\left(z_j^l\right)$$

   用矩阵形式详细表达为：
$$\left(\begin{array}{l}{\delta }_1^l\\ \\ {\delta }_2^l\\ \\ ...\\ \\ {\delta }_{n^l}^l\end{array}\right)={\left(\begin{array}{llll}{w}_{11}^l& w_{12}^l& \dots & w_{1n^l}^l\\ w_{21}^l& w_{22}^l& \dots & w_{2n^l}^l\\ ...& ...& \dots & ...\\ w_{n^{l+1}1}^l& w_{n^{l+1}2}^l& \dots & w_{n^{l+1}{n}^l}^l\end{array}\right)}^T\cdot \left(\begin{array}{l}{\delta }_1^{l+1}\\ \\ {\delta }_2^{l+1}\\ \\ ...\\ \\ {\delta }_{n^{l+1}}^{l+1}\end{array}\right)\odot {\sigma }^{\prime }\left(\begin{array}{l}{z}_1^l\\ \\ z_2^l\\ \\ ...\\ \\ z_n^l\end{array}\right)$$

   即可得到：

$${\delta }^l=\left({\left(w^{l+1}\right)}^T{\delta }^{l+1}\right)\odot {\sigma }^{\prime }\left(z^l\right)$$

• $(3)\frac{\partial C}{\partial b^l}={\delta }^l$

证明：
   取第$l$层的某一个神经元的偏置项$b_j^l$为例，根据链式法则：
$$\begin{array}{rl}\frac{\partial C}{\partial b_j^l}& =\frac{\partial C}{\partial z_j^l}\frac{\partial z_j^l}{\partial b_j^l}\\ & ={\delta }_j^l\cdot \frac{\partial \left({\sum }_{k=1}^{n^{l-1}}{w}_{jk}^l{a}_k^{l-1}+b_j^l\right)}{\partial b_j^l}\\ & ={\delta }_j^l\end{array}$$

   于是，推广之后可得：
$$\frac{\partial C}{\partial b^l}=[\frac{\partial C}{b_1^l},\frac{\partial C}{b_2^l},\dots ,\frac{\partial C}{b_{n^l}^l}{]}^T=[{\delta }_1^l,{\delta }_1^l,\dots ,{\delta }_{n^l}^l{]}^T={\delta }^l$$

• $(4)\frac{\partial C}{\partial W^l}={\delta }^l\cdot {\left(a^{l-1}\right)}^T$

证明：
   取第$l-1$层到第$l$层的某一条神经元权重$w_{jk}^l$为例，根据链式法则：
$$\begin{array}{rl}\frac{\partial C}{\partial w_{jk}^l}& =\frac{\partial C}{\partial z_j^l}\frac{\partial z_j^l}{\partial w_{jk}^l}\\ & ={\delta }_j^l\cdot \frac{\partial \left({\sum }_{k=1}^{n^{l-1}}{w}_{jk}^l{a}_k^{l-1}+b_j^l\right)}{\partial w_{jk}^l}\\ & ={\delta }_j^l\cdot a_k^{l-1}\end{array}$$

   已知矩阵$W^l$具体为：
$$W^l=\left(\begin{array}{llll}{w}_{11}^l& w_{12}^l& \dots & w_{1,n^{l-1}}^l\\ & & & \\ w_{21}^l& w_{22}^l& \dots & w_{2,n^{l-1}}^l\\ & & & \\ ...& ...& \dots & ...\\ & & & \\ w_{n^l,1}^l& w_{n^l,2}^l& \dots & w_{n^l,n^{l-1}}^l\end{array}\right)$$

   因此：
$$\frac{\partial C}{\partial W^l}=\left(\begin{array}{llll}{\delta }_1^l{a}_1^{l-1}& {\delta }_1^l{a}_2^{l-1}& \dots & {\delta }_1^l{a}_{n^{l-1}}^{l-1}\\ & & & \\ {\delta }_2^l{a}_1^{l-1}& {\delta }_2^l{a}_2^{l-1}& \dots & {\delta }_2^l{a}_{n^{l-1}}^{l-1}\\ & & & \\ ...& ...& \dots & ...\\ & & & \\ {\delta }_{n^l}^l{a}_1^{l-1}& {\delta }_{n^l}^l{a}_2^{l-1}& \dots & {\delta }_{n^l}^l{a}_{n^{l-1}}^{l-1}\end{array}\right)$$

$$=\left(\begin{array}{l}{\delta }_1^l\\ \\ {\delta }_2^l\\ \\ ...\\ \\ {\delta }_{n^l}^l\end{array}\right)\cdot \left(a_1^{l-1},a_2^{l-1},\dots ,a_{n^{l-1}}^{l-1}\right)$$

$$={\delta }^l\cdot {\left(a^{l-1}\right)}^T$$

2.8 反向传播算法整体描述

  一图看懂神经网络训练流程：

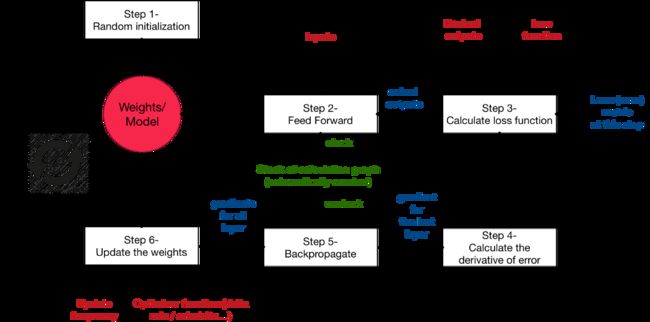
  具体分为以下6个步骤：

• 1.随机初始化
   将神经网络中的所有连接权重和偏置项随机初始化为(0,1)区间内的一个值。
• 2.正向传播
   当$l=1$时，$a^1=x$；
   当$l=2,3,\dots ,L$时：
  $$z^l=W^l{a}^{l-1}+b^l$$$$a^l=\sigma (z^l)$$
• 3.通过损失函数，计算输出层的${\delta }^L$
  $${\delta }^L=\frac{\partial C}{\partial z^L}={\nabla }_{a}C\odot {\sigma }^{\prime }\left(z^L\right)$$
• 4.误差反向传播
   当$l=L-1,L-2,\dots ,3，2$时：
  $${\delta }^l=\left({\left(w^{l+1}\right)}^T{\delta }^{l+1}\right)\odot {\sigma }^{\prime }\left(z^l\right)$$
• 5.更新权重
   当$l=2,3,\dots ,L$时，更新$W^l$和$b^l$如下：
  $$W^l=W^l-\eta \frac{\partial C}{\partial W^l}=W^l-\eta \cdot {\delta }^l(a^{l-1}{)}^T$$$$b^l=b^l-\eta \frac{\partial C}{\partial b^l}=b^l-\eta \cdot {\delta }^l$$
• 6.继续迭代，直至收敛
   迭代停止条件为：
     $\cdot$ 所有的$W，b$的变化值都小于阈值$ϵ$；
     $\cdot$ 迭代次数到达指定的最大迭代次数；

---

参考资料

1. 刘建平Pinard 《深度神经网络（DNN）模型与前向传播算法》

2. 刘建平Pinard 《深度神经网络（DNN）反向传播算法(BP)》

3. 2019/6/25更新的内容，主要参考梯度下降与反向传播（含过程推导及证明）