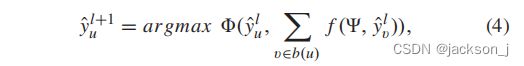Global Context Assisted Structure-Aware Vehicle Retrieval
Global Context Assisted Structure-Aware Vehicle Retrieval
车辆检索中的问题：
- 对车辆进行局部化处理，去除不相关的背景信息
- 负样本比正样本更普遍，负样本的信息在三重损失中没有得到充分利用
本文贡献：
- 我们在landmark对齐中引入局部-全局上下文网络，利用全局知识和局部结构对网络进行更新；
- 我们提出了一种结构感知四重Loss的方法，以便在车辆检索中使用多个不同的负样本；
- 构建了一个大型的车辆数据数据库；
方法：
Vehicle Detection
针对检测不精确的问题，对初始检测的边界框按20%的比例进行扩展，然后采用landmark对齐的方法对检测结果进行细化。在遮挡情况下，只有车辆被严重遮挡时，会出现假阴性（本来是车，未识别出来）结果，若只有一小部分被遮挡的情况下，检测到的置信度分数很低。
因此，使用包含相同车辆的多个帧来检测目标车辆，并将检测到的置信度最高的边界框用作对齐proposal。本文使用现成得CNN模型进行检测。
Local-Global Context in Alignment
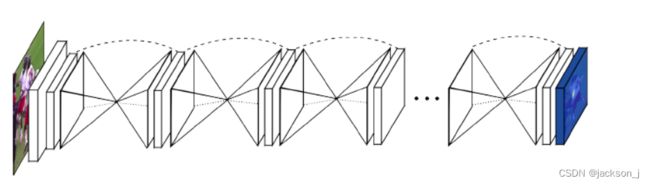
漏斗网络：这个网络架构形态就像它的名字的一样，是由一个个的漏斗状的神经网络级联起来，每一个漏斗神经网络就像编码器和解码器合成，负责提取特征和生成热图结果。整个网络使用了大量的卷积/反卷积层，池化/反池化层，ResNet以及全连接层。网络的输入是一张或者batchsize的标准大小尺寸图片（256×256），输出是该张图片缩小到一定尺寸的各个节点的热图（64×64）。
输入图像首先经过一个 7 ∗ 7 7*7 7∗7的卷积层开始，步幅为2，通道数为64；然后通过一个残差块之后，过一个最大池化层，依次通过3个残差块（通道数为128、128、128、256）。然后，利用 n n n个沙漏网络来预测landmark的位置。
Local Inference Network（LIN）和Global-Local Context Network (GLCN)生成每个landmark的激活图，激活图的最大价值就是提供特定landmark的位置。
landmark的数量和位置是根据经验选择的。
设一个图 G = { V , E } G = \{V,E\} G={V,E}表示车辆各landmark之间的结构关系，节点 v u v_u vu对应第 u u u个landmark，边 e u v e_{uv} euv用来描述第 u u u个和第 v v v个节点之间的关系。可以使用成对约束来强制landmark与groundtruth之间的距离。
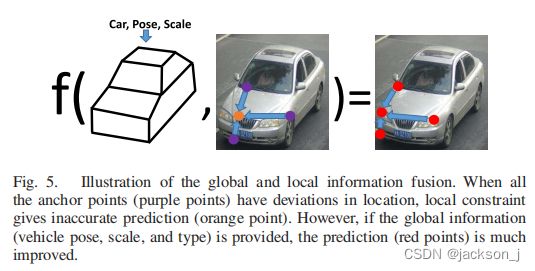
但是当相邻的点（下图中紫色点）都偏离了正确的位置并产生偏移时，就没有办法利用两两关系来得到改进的结果（下图中橙色点）。
因此，我们需要一个可以同时更好地评估多个landmark的约束，即关于场景和物体的全局信息，包括观测视图(或车辆姿态)、车辆规模和车辆类型。
这是因为:
-
车辆外观会随着观察视野的变化而变化;
-
如果车辆距离摄像机较远，车辆在图像中的尺度较小，地标之间的距离会减小;
-
不同类型的车辆，如轿车和公交车，其框架不同，通用模型的通用性较差；
多点错误与这些因素有关。如果所有这些因素都被规范化，多点错误可以得到改善。
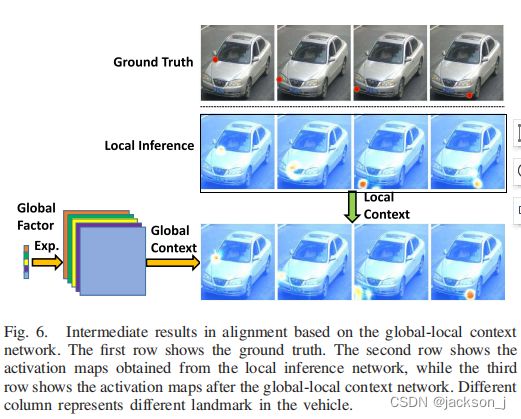
因此，除了沙漏结构的LIN外，我们还提出了一个全局推理网络(GIN)和一个全局-局部上下文网络来显式提取语义和姿态知识，并利用这些全局信息来辅助基于局部结构的地标定位。
GIN的输出对应全局因子 ψ \psi ψ，其中 ψ = { a , s , t } \psi=\{a,s,t\} ψ={a,s,t}为影响图像中地标位置的全局因子;a表示相机视图，我们用俯仰、平贴和相机的旋转角度来描述;s为车辆规模;t是车辆的类型，如小汽车、面包车或公共汽车等。我们会将推断出的全局因子扩展到与局域推断网络得到的热图具有相同的空间大小。然后，将扩展的全局因子和局部热图串联起来，通过另一个沙漏子网络对局部化结果进行微调。
Global-Local Context Network的损失函数为：
L g l o b a l − l o c a l ( ψ ) = ∑ u ϕ ( y u ^ , ∑ v ϵ b ( u ) f ( ψ , y v ^ ) ) L_{global-local}(\psi) = \sum_{u}{}\phi(\hat{y_u},\sum_{v\epsilon b(u)}{}f(\psi, \hat{y_v})) Lglobal−local(ψ)=u∑ϕ(yu^,vϵb(u)∑f(ψ,yv^))
其中 b ( u ) b(u) b(u)表示第 u u u个节点的相邻节点， f ( ψ , y v ^ ) f(\psi, \hat{y_v}) f(ψ,yv^)输入第v个预测的邻居landmark y v ^ \hat{y_v} yv^和全局因子 ψ \psi ψ返回微调之后的定位结果。 ϕ \phi ϕ是衡量LIN得到的预测landmark和全局局部线索得到的landmark之间的相容性的函数。
在推理阶段，可以通过迭代的方式使用全局-局部结构损失函数来提高精确度：
其中， y ^ u l \hat{y}_u^l y^ul是在第 l l l次迭代中第 u u u个landmark，可以根据全局约束和局部约束对其进行更新。
Structure-Aware Quadruple Loss in Retrieval
成对损失可以根据是否属于同一车辆产生不同种类的损失函数，例如：
L c o n t r a = Y ( i , j ) δ x i , x j + ( 1 − Y ( i , j ) ) m a x { τ − δ x i , x j , 0 } L_{contra} = Y(i,j)\delta_{x^i,x^j}+(1-Y(i,j))max\{\tau-\delta_{x^i,x^j},0\} Lcontra=Y(i,j)δxi,xj+(1−Y(i,j))max{τ−δxi,xj,0}
其中， δ x i , x j = d ( f ( x i ) , f ( x j ) ) \delta_{x^i,x^j}=d(f(x^i), f(x^j)) δxi,xj=d(f(xi),f(xj))为特征图 f f f中图像 x i x^i xi和 x j x^j xj的距离。 Y ( i , j ) ϵ { 0 , 1 } Y(i,j)\epsilon\{0,1\} Y(i,j)ϵ{0,1}表示ID为i和ID为j是否属于统一对象（1）或不属于统一对象（0）。如果 x i x^i xi和 x j x^j xj匹配，则它们的特征映射之间的差异最小;否则，差值将最大化。
Triple Loss惩罚了负样本到锚点的距离小于正样本的情况，公式如下：
L t r i p l e = m a x { α + δ p o s − δ n e g , 0 } L_{triple} = max\{\alpha+\delta_{pos}-\delta_{neg}, 0\} Ltriple=max{α+δpos−δneg,0}
其中， δ p o s = d ( f ( x a ) , f ( x p ) ) \delta_{pos}=d(f(x^a),f(x^p)) δpos=d(f(xa),f(xp))是由锚样本 x a x^a xa及其正样本 x p x^p xp获得的特征图之间的距离, δ n e g = d ( f ( x a ) , f ( x n ) ) \delta_{neg}=d(f(x^a),f(x^n)) δneg=d(f(xa),f(xn))是由锚样本 x a x^a xa及其负样本 x n x^n xn获得的特征图之间的距离, α \alpha α是一个常数参数，用于获取边界。
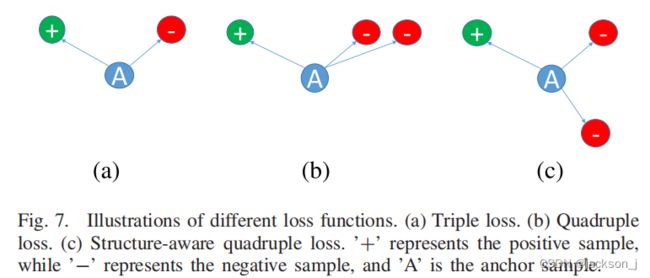
为了充分利用负样本中的信息，我们将三倍损失扩展为四倍损失，并使用两个负样本来优化网络中的权值，如图上(b)所示。
L q u a d r u = m a x { α + δ p o s − δ n e g 1 , 0 } + m a x { β + δ p o s − δ n e g 2 , 0 } L_{quadru} = max\{\alpha+\delta_{pos}-\delta_{neg1}, 0\}+max\{\beta+\delta_{pos}-\delta_{neg2}, 0\} Lquadru=max{α+δpos−δneg1,0}+max{β+δpos−δneg2,0}
采用硬样本挖掘方法可以得到 x n 1 x^{n1} xn1和 X n 2 X^{n2} Xn2，即选取特征空间中与锚样距离最小的负样本。
在某些情况下，最硬样本 x n 1 x^{n1} xn1和 x n 2 x^{n2} xn2具有相似的外观，在特征空间中彼此接近。为了增强负样本的多样性，我们修改了硬样本挖掘的方法，如图7©所示。仍然选择 x n 1 x^{n1} xn1作为与锚点样本距离最小的负样本，但在约束条件下选择 x n 2 x^{n2} xn2，使与锚点样本的距离和与 x n 1 x^{n1} xn1的相似度都很小。
x n 2 = a r g m i n { δ n e g 2 + ϕ ( x n 1 , x n 2 ) } x^{n2} = argmin\{\delta_{neg2}+\phi(x^{n1},x^{n2})\} xn2=argmin{δneg2+ϕ(xn1,xn2)}
件下选择 x n 2 x^{n2} xn2，使与锚点样本的距离和与 x n 1 x^{n1} xn1的相似度都很小。
x n 2 = a r g m i n { δ n e g 2 + ϕ ( x n 1 , x n 2 ) } x^{n2} = argmin\{\delta_{neg2}+\phi(x^{n1},x^{n2})\} xn2=argmin{δneg2+ϕ(xn1,xn2)}
其中， ϕ ( x n 1 , x n 2 ) \phi(x^{n1},x^{n2}) ϕ(xn1,xn2)为负样本 x n 1 x^{n1} xn1和 x n 2 x^{n2} xn2的相似度。