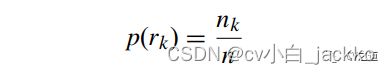【matlab图像处理】直方图均衡化
中国史之【犬戎之祸】：
公元前771年，西夷犬戎攻入西周都城镐京（今陕西西安），杀周幽王，镐京残破，于是继位的周平王东迁至雒邑（今河南洛阳）。犬戎之祸为西周与东周历史的分界事件。
——来源：全历史APP
【路漫漫其修远兮，吾将上下而求索】
今天介绍图像的直方图均衡化。本内容参考自《实用MATLAB图像和视频处理》第9章。
- 对于matlab2021的安装，可以参考公众号【CV之道】的文章：【matlab安装】手把手图文并茂安装matlab2021（win10版）
1、直方图均衡化
直方图均衡化是指：通过改变一幅图像的灰度分布，以得到一个均匀的直方图，其中每种灰度值的像素所占的百分比相同。
为进行直方图均衡化，需要使用一个辅助函数，称为变换函数T(r)。其需要满足两个准则：
（1）T(r) 在像素范围内（0 <= r <= L-1）应该是单调递增的函数。
（2）对于0 <= r <= L-1，有0 <= T(r) <= L-1。
最常用的变换函数是原始概率密度函数的累积分布函数（cdf），公式如下：
2、直方图均衡化具体计算例子
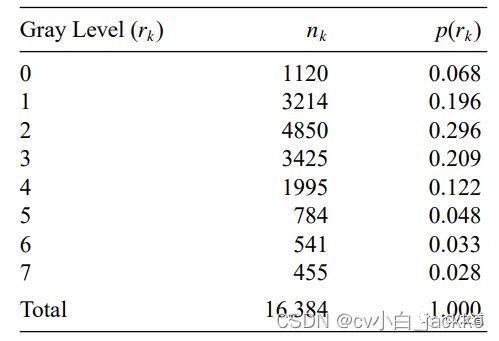
例如，下表是一个8灰度级的128x128=16384像素的图像直方表。
其中，第2列表示该灰度级的数目，第3列为该灰度级占总像素的百分比，其计算公式很简单，比如第0灰度值的百分比是：1120/16384=0.068。
我们已经得到了p，那么，计算s就是前面项的累加。比如，
s0=p0=0.068，
s1=p0+p1=0.068+0.196=0.264，
s2=p0+p1+p2=0.264+0.296=0.560，
以此类推。最终有s3=0.769，s4=0.891，s5=0.939，s6=0.972，当然，s7=1。
又因为图像被量化为0~7共8个灰度级，所以每个s必须要四舍五入到最近的灰度级，只需要将对应的数乘7。如：
s0=0.068x7=0.476=0
s1=0.264x7=1.848=2
s2=0.560x7=3.92=4
s3=0.769x7=5.383=5
s4=0.891x7=6.237=6
s5=0.939x7=6.573=7
s6=0.972x7=6.804=7
s7=1x7=7
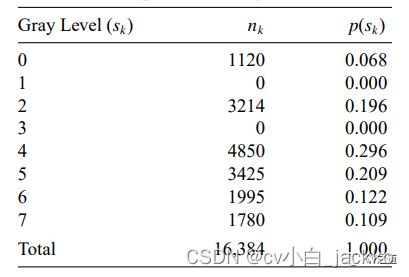
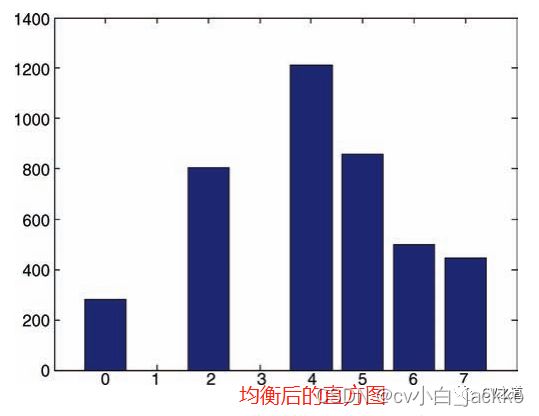
综上，均衡化后的灰度值只有0、2、4、5、6、7这6个数。最终均衡化的表格如下：
3、图像直方图均衡化例子
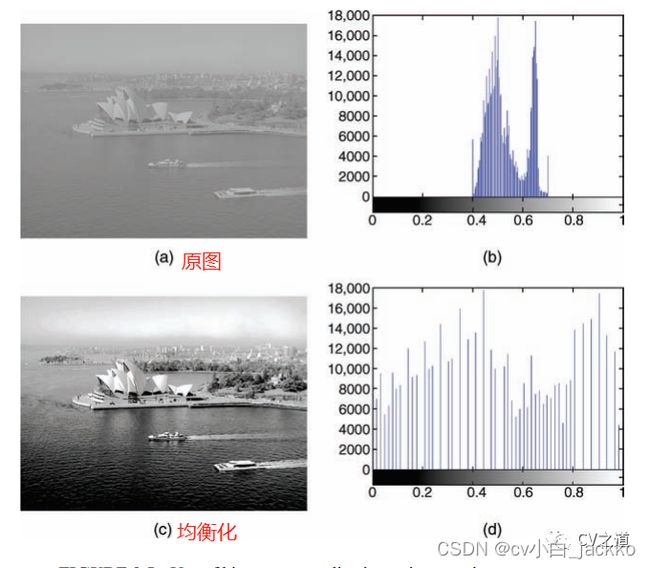
下图为使用图像直方图均衡化来增强一幅256个灰度级的600x800图像的例子。其中，(a）为原图，对应的直方图是（b）。而均衡化后的图为（c），对应直方图为（d）。
从图上我们可以明显看到效果，原图是一片暗淡，均衡化后目标都变得清晰了。但是，我们可以看到天空部分，有一些虚假的轮廓，这可以看做直方图均衡化的一些“副作用”。
另外，histeq操作的是全局直方图均衡化。其实，adapthisteq进行局部直方图均衡化效果更好。因为全局是对整个图片计算映射，但有时候，我们只需要对局部区域进行操作，这就需要局部均衡化。
这个局部均衡化，其实就是滑动窗口功能，利用一个矩阵滑动窗，对整个图像扫一遍，对于窗口内的像素进行均衡化。这其实和卷积操作也很类似。
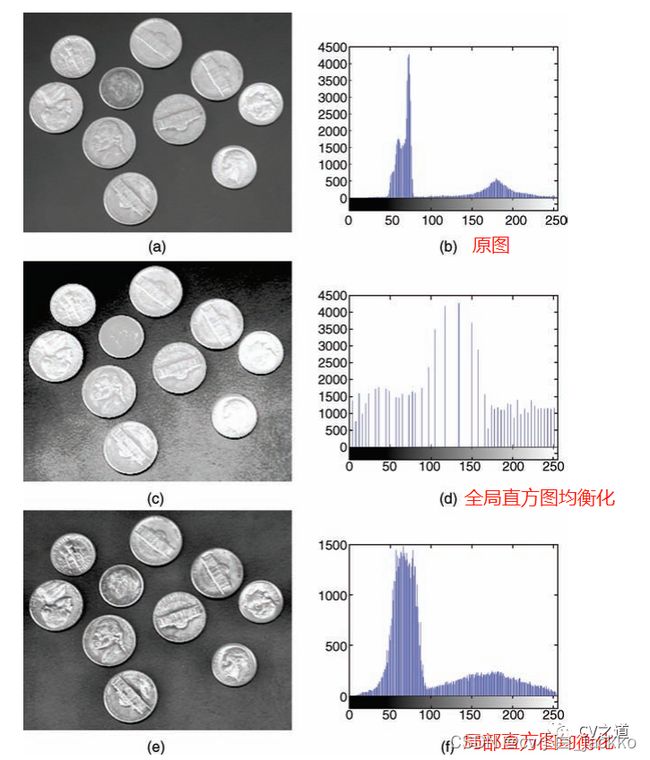
下图是一个效果对比。
另外，直方图操作还有直接直方图规定化、直方图滑动、伸展、收缩等等，由于不是重点，只需要实践一下函数即可。
以上是本期内容，建议自己动手来实践一下。如果需要图片和代码，可以关注公众号，回复关键字【matlab代码】即可获得。我会上传到云盘。
【声明】：学习笔记基于互联网上各种学习资源的个人整理。
以上是本期内容，下期介绍图像处理的直方图均衡化实践。
我叫小保，一名计算机视觉爱好者、学习者、追随者，欢迎关注我【CV之道】一起学习。