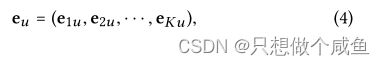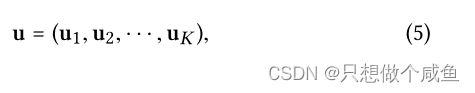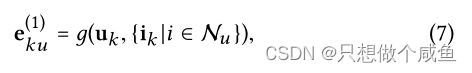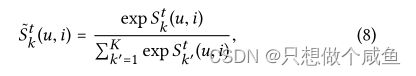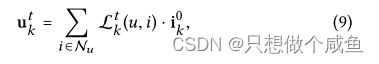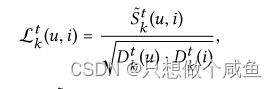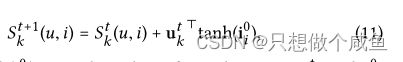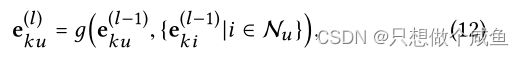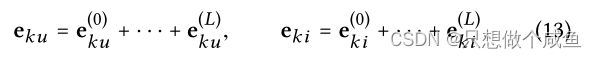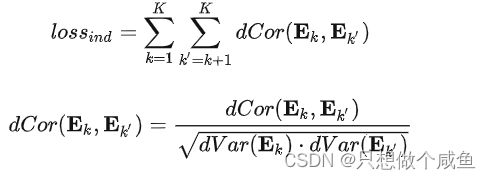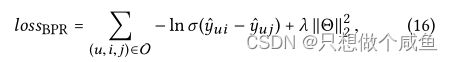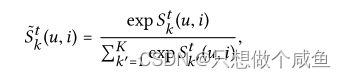只想做个咸鱼

DGCF:Disentangled Graph Collaborative Filtering论文及代码

一、前言

关注用户意图粒度更细的用户-项目关系。因此，设计了一个新的模型——解纠缠图协同过滤（DGCF），以解纠缠这些因素并产生解纠缠的表示。通过为每个用户项交互的意图建模分布，我们迭代地细化意图感知交互图和表示。同时，我们鼓励不同意图的独立性。这导致了分离的表示，有效地提取出与每个意图相关的信息。

协作过滤（CF）侧重于历史用户项目交互（例如，购买、点击），它假定行为相似的用户可能对项目有类似的偏好。对基于CF的推荐器进行了广泛的研究，用户-物品交互关系的建模发展过程可以概括为

① 单个ID（用户、物品）的embedding

② 融入个人历史信息的embedding（一阶连通性）

③ 利用整体交互图的embedding（高阶连通性）

这项工作做出了以下主要贡献：

我们强调了不同用户物品关系在协同过滤中的重要性，对这种关系的建模可以带来更好的表示和可解释性。

我们提出了一种新的模型DGCF，它以更精细的用户意图粒度来考虑用户-项目关系，并生成不纠缠的表示。

任务由两个子任务组成：

1、在用户意图的粒度级别上探索用户与项目的关系，

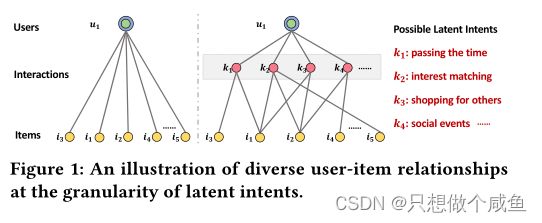
一个用户的行为会受到多种意图的影响，例如消磨时间、匹配特定兴趣爱好以及为家人等其他人购物。

学习每个行为的用户意图的分布A（u，i），

2、生成未纠缠的CF表示

提取与各个意图相关的信息作为表示的独立部分。更正式地说，我们的目标是设计一个嵌入函数f（·），以便为用户u输出一个解纠缠的表示eu，它由K个独立分量组成：

二、DGCF模型介绍

（PS：模型概述：模型设置 K 个意图，每个意图都对应一个子图。在 K 个子图上分别学习用户和物品的嵌入，最后组合起来形成最终的嵌入。）

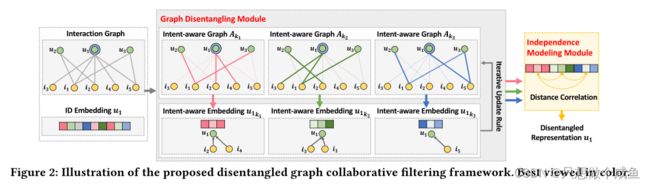
提出了一种被称为DGCF的解缠结图协作过滤，如图2所示。它由两个关键组件组成，以实现解缠结：

1）图解缠结模块，它首先将每个用户/项目嵌入到块中，将每个块与意图耦合，然后将新的邻居路由机制并入图神经网络，以便解开交互图并细化意图感知表示；

2）独立性建模模块，该模块使用距离相关性作为正则化器来鼓励意图的独立性。DGCF最终生成具有意图感知解释图的解纠缠表示。

1、关于GNN的图分离模块

（1）意向感知嵌入初始化

主流CF仅将用户/项目ID参数化为整体表示，我们还将ID嵌入分离为K个块，将每个块与潜在意图相关联。用户嵌入被初始化为：

其中 $u\ni R^{d}$ 是用于捕获u的固有特性的ID嵌入； $u_{k}\ni R^{\frac{d}{K}}$ 是u对第K个意图的分块表示。

（2）意向感知图初始化

以前的工作不足以描述行为背后的丰富用户意图，因为它们只利用一个用户-项目交互图或同质评级图来展示用户-项目关系。

定义了一组得分矩阵{Sk|∀k∈ ｛1，··，K｝｝。注意图感知矩阵Sk，每个条目Sk（u，i）表示用户u和项目i之间的交互。

此外，对于每个交互，我们可以构造一个得分向量S（u，i）=（S1（u，i），··，SK（u），i））,我们统一初始化每个得分向量，如下所示：

其假定在建模开始时意图的贡献相等。因此，这种得分矩阵Sk可以被视为意图感知图的邻接矩阵。

(3)图形分离层

目标是从用户和项目之间的高阶连接中提取有用信息，而不仅仅是ID嵌入。为此，我们设计了一个新的图分离层，该层配备了邻居路由和嵌入传播机制，其目标是在传播信息时区分每个用户项连接的自适应角色。

$e_{ku}^{1}$ 表示用户 u 在子图 k 上的 1 阶聚合信息，中间使用了邻居路由机制来迭代更新

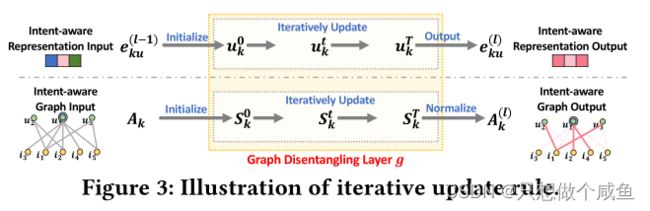
迭代更新规则

路由机制：首先，我们使用嵌入传播机制来更新意图感知嵌入，基于意图感知图；然后，我们依次利用更新的嵌入来细化图并输出意图上的分布。特别是，我们设置T次迭代来实现这种迭代更新。

在GCN的某一层中，其迭代更新的过程为：子图邻域聚合 → 得到用户(物品)嵌入 → 调整子图连边权重 → 子图邻域聚合 → ....

交叉意图嵌入传播

对于目标交互（u，i），我们有得分向量，比如{Sk（u，i）|∀k∈ {1，··，K}}。为了获得其在所有意图上的分布，我们随后通过softmax函数对这些系数进行归一化：

其能够说明哪些意图应该得到更多关注以解释每个用户行为（u，i）。

我们在单个图上执行嵌入传播，从而将对用户意图k有影响的信息编码到表示中。更正式地说，加权和聚合器定义为：

于是我们根据概率进行信息的传播聚合，上面包括了拉普拉斯矩阵归一化操作。

需要注意的是：

由于之前在LightGCN一文中已经证明特征转换和非线性变换对于协同过滤来说没有作用，甚至会降低效果，自连接也是没有用的。所以这篇文章中的GCN也只包括了邻域聚合操作。
在迭代过程中，使用的始终是物品的初始嵌入 ik0 ，只有到GCN的下一层时，才会更新。

意向感知图更新。

基于新计算出的嵌入 $u_{k}^{t}$ ，更新

至此一次迭代计算就完成了，接下来基于新的邻接矩阵重复上述步骤。当 T 次迭代都结束时，得到用户在当前GCN层的嵌入

（4）层结合

高阶连接性中捕捉用户意图

在经过 L 层的传播聚合之后，将不同层得到的嵌入相加得到最终表示：

（5）独立建模

考虑到上面每种意图得到的用户物品嵌入可能还存在冗余，为了使每种意图之间保持独立，作者引入了一个距离相关的函数：

2、模型优化

话不多说，BPR损失函数

三、实验部分内容

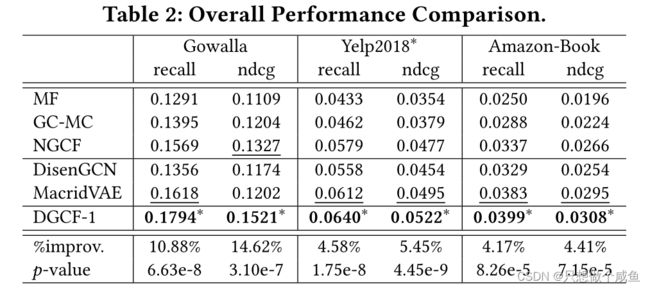
RQ1：与现有模型相比，DGCF的表现如何？

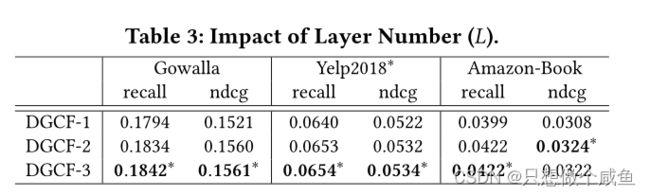
RQ2：不同组件（例如，层编号、意图编号、独立建模）如何影响DGCF的结果？

RQ3：DGCF是否可以提供对解缠结表示的深入分析，同时对潜在用户意图和表示的可解释性进行解缠结？

1、Performance Comparison (RQ1)

2、 Study of DGCF (RQ2)消融实验

图形分解层的数量、潜在用户意图的数量以及独立建模如何影响模型。

四、DGCF代码

1数据集及参数基本信息

n_users=4874, n_items=2406
n_interactions=52957
n_train=37027, n_test=15930, sparsity=0.00452
************************* Run with following settings  ***************************
Namespace(Ks='[20, 40, 60, 80, 100]', batch_size=1024, corDecay=0.01, cor_flag=1, data_path='../Data/', dataset='office', early=10, embed_name='', embed_size=128, epoch=2000, gpu='2', layer_size='[128]', lr=0.001, n_factors=4, n_iterations=2, n_layers=1, pick=0, pick_scale=10000000000.0, pretrain=0, proj_path='', regs='[1e-3,1e-4,1e-4]', save_flag=0, save_name='best_model', show_step=3, test_flag='part', verbose=1)
************************************************************************************
already load adj matrix (7280, 7280) 0.0299530029296875

2、意向感知图初始化

对于每个交互，我们可以在K个潜在意图构造得分向量。我们统一初始化每个得分向量，如下所示：

$S\left ( u,i \right )=\left ( 1,...,1 \right )$

其假定在建模开始时意图的贡献相等。因此，这种得分矩阵Sk可以被视为意图感知图的邻接矩阵。

    plain_adj, norm_adj, mean_adj, pre_adj = data_generator.get_adj_mat()

    all_h_list, all_t_list, all_v_list = load_adjacency_list_data(plain_adj)#得到邻接矩阵中的 row col value

    A_values_init = create_initial_A_values(args.n_factors, all_v_list)#对每一个u-i交互默认初始意图为1   4*74054

    config['norm_adj'] = plain_adj
    config['all_h_list'] = all_h_list
    config['all_t_list'] = all_t_list

3、图形分离层

单个意图通道中，我们的目标是从用户和项目之间的高阶连接中提取有用信息，而不仅仅是ID嵌入。为此，我们设计了一个新的图分离层，该层配备了邻居路由和嵌入传播机制，其目标是在传播信息时区分每个用户项连接的自适应角色。

（1）迭代更新规则

子图邻域聚合 → 得到用户(物品)嵌入 → 调整子图连边权重 → 子图邻域聚合 → ....

    def _create_star_routing_embed_with_P(self, pick_ = False):
        '''
        pick_ : True, the model would narrow the weight of the least important factor down to 1/args.pick_scale.
        pick_ : False, do nothing.
        '''
        p_test = False
        p_train = False

        A_values = tf.ones(shape=[self.n_factors, len(self.all_h_list)])#4*74054
        # get a (n_factors)-length list of [n_users+n_items, n_users+n_items]

        # load the initial all-one adjacency values
        # .... A_values is a all-ones dense tensor with the size of [n_factors, all_h_list].
        

        # get the ID embeddings of users and items
        # .... ego_embeddings is a dense tensor with the size of [n_users+n_items, embed_size];
        # .... all_embeddings stores a (n_layers)-len list of outputs derived from different layers.
        ego_embeddings = tf.concat([self.weights['user_embedding'], self.weights['item_embedding']], axis=0)#得到初始embedd u+i * embedd—size
        all_embeddings = [ego_embeddings]#7208*128
        all_embeddings_t = [ego_embeddings]

        output_factors_distribution = []
        
        factor_num = [self.n_factors, self.n_factors, self.n_factors]#4
        iter_num = [self.n_iterations, self.n_iterations, self.n_iterations]
        for k in range(0, self.n_layers):
            # prepare the output embedding list
            # .... layer_embeddings stores a (n_factors)-len list of outputs derived from the last routing iterations.
            n_factors_l = factor_num[k]#4
            n_iterations_l = iter_num[k]#2
            layer_embeddings = []
            layer_embeddings_t = []
            
            # split the input embedding table
            # .... ego_layer_embeddings is a (n_factors)-leng list of embeddings [n_users+n_items, embed_size/n_factors]
            ego_layer_embeddings = tf.split(ego_embeddings, n_factors_l, 1)#拆分初始embedd   list4  7280*32
            ego_layer_embeddings_t = tf.split(ego_embeddings, n_factors_l, 1) 

            # perform routing mechanism
            for t in range(0, n_iterations_l):
                iter_embeddings = []
                iter_embeddings_t = []
                A_iter_values = []

                # split the adjacency values & get three lists of [n_users+n_items, n_users+n_items] sparse tensors
                # .... A_factors is a (n_factors)-len list, each of which is an adjacency matrix
                # .... D_col_factors is a (n_factors)-len list, each of which is a degree matrix w.r.t. columns
                # .... D_row_factors is a (n_factors)-len list, each of which is a degree matrix w.r.t. rows
                if t == n_iterations_l - 1:
                    p_test = pick_
                    p_train = False

                A_factors, D_col_factors, D_row_factors = self._convert_A_values_to_A_factors_with_P(n_factors_l, A_values, pick= p_train)
                A_factors_t, D_col_factors_t, D_row_factors_t = self._convert_A_values_to_A_factors_with_P(n_factors_l, A_values, pick= p_test)
                for i in range(0, n_factors_l):
                    # update the embeddings via simplified graph convolution layer
                    # .... D_col_factors[i] * A_factors[i] * D_col_factors[i] is Laplacian matrix w.r.t. the i-th factor
                    # .... factor_embeddings is a dense tensor with the size of [n_users+n_items, embed_size/n_factors]
                    factor_embeddings = tf.sparse_tensor_dense_matmul(D_col_factors[i], ego_layer_embeddings[i])#  embeddin 7280*32
                    factor_embeddings_t = tf.sparse_tensor_dense_matmul(D_col_factors_t[i], ego_layer_embeddings_t[i])

                    factor_embeddings_t = tf.sparse_tensor_dense_matmul(A_factors_t[i], factor_embeddings_t)
                    factor_embeddings = tf.sparse_tensor_dense_matmul(A_factors[i], factor_embeddings)

                    factor_embeddings = tf.sparse_tensor_dense_matmul(D_col_factors[i], factor_embeddings)
                    factor_embeddings_t = tf.sparse_tensor_dense_matmul(D_col_factors_t[i], factor_embeddings_t)

                    iter_embeddings.append(factor_embeddings)#7280*32
                    iter_embeddings_t.append(factor_embeddings_t)
                    
                    if t == n_iterations_l - 1:
                        layer_embeddings = iter_embeddings
                        layer_embeddings_t = iter_embeddings_t

                    # get the factor-wise embeddings
                    # .... head_factor_embeddings is a dense tensor with the size of [all_h_list, embed_size/n_factors]
                    # .... analogous to tail_factor_embeddings
                    head_factor_embedings = tf.nn.embedding_lookup(factor_embeddings, self.all_h_list)#74054*32  这是一阶聚合embed
                    tail_factor_embedings = tf.nn.embedding_lookup(ego_layer_embeddings[i], self.all_t_list)#74054*32  这是初始embed

                    # .... constrain the vector length
                    # .... make the following attentive weights within the range of (0,1)
                    head_factor_embedings = tf.nn.l2_normalize(head_factor_embedings, axis=1)  #标准化
                    tail_factor_embedings = tf.nn.l2_normalize(tail_factor_embedings, axis=1)

                    # get the attentive weights
                    # .... A_factor_values is a dense tensor with the size of [all_h_list,1]
                    A_factor_values = tf.reduce_sum(tf.multiply(head_factor_embedings, tf.tanh(tail_factor_embedings)), axis=1)#74054    公 式11

                    # update the attentive weights
                    A_iter_values.append(A_factor_values)#存储注意力权重

                # pack (n_factors) adjacency values into one [n_factors, all_h_list] tensor
                A_iter_values = tf.stack(A_iter_values, 0)#4*74054
                # add all layer-wise attentive weights up.
                A_values += A_iter_values
                
                if t == n_iterations_l - 1:
                    #layer_embeddings = iter_embeddings
                    output_factors_distribution.append(A_factors)

            # sum messages of neighbors, [n_users+n_items, embed_size]
            side_embeddings = tf.concat(layer_embeddings, 1)#7280*128    7280*32 这是一阶聚合后的
            side_embeddings_t = tf.concat(layer_embeddings_t, 1)
            
            ego_embeddings = side_embeddings
            ego_embeddings_t = side_embeddings_t
            # concatenate outputs of all layers
            all_embeddings_t += [ego_embeddings_t]
            all_embeddings += [ego_embeddings]

        all_embeddings = tf.stack(all_embeddings, 1)
        all_embeddings = tf.reduce_mean(all_embeddings, axis=1, keepdims=False)

        all_embeddings_t = tf.stack(all_embeddings_t, 1)
        all_embeddings_t = tf.reduce_mean(all_embeddings_t, axis=1, keep_dims=False)

        u_g_embeddings, i_g_embeddings = tf.split(all_embeddings, [self.n_users, self.n_items], 0)
        u_g_embeddings_t, i_g_embeddings_t = tf.split(all_embeddings_t, [self.n_users, self.n_items], 0)

        return u_g_embeddings, i_g_embeddings, output_factors_distribution, u_g_embeddings_t, i_g_embeddings_t

（2）交叉意图嵌入传播（附属于上面）

在迭代t，对于目标交互 $\left (u,i \right )$ ，我们有得分向量，比如{Sk（u，i）|∀k∈ {1，··，K}}。为了获得其在所有意图上的分布，我们随后通过softmax函数对这些系数进行归一化：