- 遥感影像的切片处理
sand&wich
计算机视觉python图像处理
在遥感影像分析中,经常需要将大尺寸的影像切分成小片段,以便于进行详细的分析和处理。这种方法特别适用于机器学习和图像处理任务,如对象检测、图像分类等。以下是如何使用Python和OpenCV库来实现这一过程,同时确保每个影像片段保留正确的地理信息。准备环境首先,确保安装了必要的Python库,包括numpy、opencv-python和xml.etree.ElementTree。这些库将用于图像处理
- Python实现下载当前年份的谷歌影像
sand&wich
python开发语言
在GIS项目和地图应用中,获取最新的地理影像数据是非常重要的。本文将介绍如何使用Python代码从Google地图自动下载当前年份的影像数据,并将其保存为高分辨率的TIFF格式文件。这个过程涉及地理坐标转换、多线程下载和图像处理。关键功能该脚本的核心功能包括:坐标转换:支持WGS-84与WebMercator投影之间转换,以及处理中国GCJ-02偏移。自动化下载:多线程下载地图瓦片,提高效率。图像
- Python实现TIFF 文件转换为 PNG 和 JPG 格式
sand&wich
python开发语言
在日常的图像处理工作中,可能会遇到需要将TIFF格式的图像转换为其他格式的情况,例如PNG和JPG。下面,本文将介绍如何使用Python和GDAL库实现这一功能。准备工作在开始之前,请确保已经安装了必要的库:GDAL(GeospatialDataAbstractionLibrary)可以使用以下命令安装GDAL:pipinstallgdal代码实现以下是一个将TIFF文件转换为PNG文件的示例代码
- OpenCV图像处理技术(Python)——入门
森屿_
opencv
©FuXianjun.AllRightsReserved.OpenCV入门图像作为人类感知世界的视觉基础,是人类获取信息、表达信息的重要手段,OpenCV作为一个开源的计算机视觉库,它包括几百个易用的图像成像和视觉函数,既可以用于学术研究,也可用于工业邻域,它于1999年由因特尔的GaryBradski启动,OpenCV库主要由C和C++语言编写,它可以在多个操作系统上运行。1.1图像处理基本操作
- opencv学习:图像旋转的两种方法,旋转后的图片进行模板匹配代码实现
夜清寒风
学习opencv机器学习人工智能计算机视觉
图像旋转在图像处理中,rotate和rot90是两种常见的图像旋转方法,它们在功能和使用上有一些区别。下面我将分别介绍这两种方法,并解释它们的主要区别rot90方法rot90方法是NumPy提供的一种数组旋转函数,它主要用于对二维数组(如图像)进行90度的旋转。这个方法比较简单,只支持90度的倍数旋转,不支持任意角度旋转。使用NumPy进行旋转使用NumPy的rot90函数对模板图像进行旋转操作。
- Python OpenCV图像处理:从基础到高级的全方位指南
极客代码
玩转Python开发语言pythonopencv图像处理计算机视觉
目录第一部分:PythonOpenCV图像处理基础1.1OpenCV简介1.2PythonOpenCV安装1.3实战案例:图像显示与保存1.4注意事项第二部分:PythonOpenCV图像处理高级技巧2.1图像变换2.2图像增强2.3图像复原第三部分:PythonOpenCV图像处理实战项目3.1图像滤波3.2图像分割3.3图像特征提取第四部分:PythonOpenCV图像处理注意事项与优化策略4
- 服务器状态监控php源码,服务器状态监控_监控Linux服务器网站状态的SHELL脚本
温糯米
服务器状态监控php源码
摘要腾兴网为您分享:监控Linux服务器网站状态的SHELL脚本,蜗牛集市,同花顺,探客宝,手柄助手等软件知识,以及日期倒计时插件,云南省教育资源公共,rui手机桌面,小屁孩桌面便签,合金装备崛起复仇,朝夕日历,photoshop图像处理软件,一年级学生每日计划表,悟空找房,饿了吗外卖商家版,逃生,中国民宿网,realpolitiks,交通安全知识竞赛,雅思流利说等软件it资讯,欢迎关注腾兴网。1
- 多模态Transformer之文本与图像联合建模 - Transformer教程
shandianfk_com
ChatGPTTransformertransformer深度学习人工智能
大家好,今天我们来聊聊一个既前沿又有趣的话题——多模态Transformer,特别是文本与图像的联合建模。对于很多小伙伴来说,Transformer这个词已经不陌生了,但它不仅仅应用于自然语言处理,还能在图像处理、甚至是多模态数据的处理上大显身手。接下来,我会带大家深入了解什么是多模态Transformer,以及它是如何实现文本与图像的联合建模的。Transformer简介首先,我们简单回顾一下T
- Matlab2024a安装教程
是阿宇呢
信息可视化开发语言
MATLAB是一款商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分,可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等,主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。1.解压安装包:①鼠标右击【MATLABR2024a(64bit)
- 图像处理的作用(6幅图诗)
静月园
静月园著2020年1月️4日1自然力出现的图形画面,即无序,又有形。奇妙令人联想无限。好象理石花纹,又类似草木树植。2为何要如此色彩?好奇怪哦!自然的物态鬼斧神工。3孩童们信手涂鸦,但是脑控制了手的动作,所绘画的物体形状代表了孩子们对环境人物的所看,所听,所理解的形状。脑的心理活动影像,被转换成手的动作输出到笔尖的移动动作上,于是我们看到了简单的结构形状图。而对于我们的写作者来说,我们的作家脑内有
- OpenCV高阶操作
富士达幸运星
opencv人工智能计算机视觉
在图像处理与计算机视觉领域,OpenCV(OpenSourceComputerVisionLibrary)无疑是最为强大且广泛使用的工具之一。从基础的图像读取、1.图片的上下,采样下采样(Downsampling)下采样通常用于减小图像的尺寸,从而减少图像中的像素数。这个过程可以通过多种方法实现,但最常见的是通过图像金字塔中的pyrDown函数(在OpenCV中)或其他类似的滤波器(如平均池化、最
- opencv 之 实战项目 识别银行卡上的数字
SEVEN-YEARS
opencv计算机视觉人工智能
OpenCV之实战项目:识别银行卡上的数字引言在日常生活中,银行卡的识别是一个常见的需求,特别是在金融领域。本实战项目旨在使用OpenCV库来识别银行卡上的数字。我们将通过模板匹配的方法,结合图像处理技术,来准确识别银行卡上的数字序列。项目准备本项目需要安装Python和OpenCV库。确保已经安装了必要的库,并准备好银行卡图像和数字模板图像。实验素材定义函数importcv2defsort_co
- 【图像压缩】奇异值分解SVD灰色图像压缩(可设置压缩比)【含Matlab源码 4358期】
Matlab武动乾坤
Matlab图像处理(进阶版)matlab
✅博主简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,Matlab项目合作可私信。个人主页:海神之光代码获取方式:海神之光Matlab王者学习之路—代码获取方式⛳️座右铭:行百里者,半于九十。更多Matlab仿真内容点击Matlab图像处理(进阶版)路径规划(Matlab)神经网络预测与分类(Matlab)优化求解(Matlab)语音处理(Matlab)信号处理(Matlab)车间调度
- Python OpenCV精讲系列 - 高级图像处理技术(五)
极客代码
PythonOpenCV精讲pythonopencv图像处理开发语言人工智能计算机视觉
⚡️⚡️专栏:PythonOpenCV精讲⚡️⚡️本专栏聚焦于Python结合OpenCV库进行计算机视觉开发的专业教程。通过系统化的课程设计,从基础概念入手,逐步深入到图像处理、特征检测、物体识别等多个领域。适合希望在计算机视觉方向上建立坚实基础的技术人员及研究者。每一课不仅包含理论讲解,更有实战代码示例,助力读者快速将所学应用于实际项目中,提升解决复杂视觉问题的能力。无论是入门者还是寻求技能进
- K-means 算法的介绍与应用
小魏冬琅
matlab算法kmeans机器学习
目录引言K-means算法的基本原理表格总结:K-means算法的主要步骤K-means算法的MATLAB实现优化方法与改进K-means算法的应用领域表格总结:K-means算法的主要应用领域结论引言K-means算法是一种经典的基于距离的聚类算法,在数据挖掘、模式识别、图像处理等多个领域中得到了广泛应用。其核心思想是将相似的数据对象聚类到同一个簇中,而使得簇内对象的相似度最大、簇间的相似度最小
- 基于VGG的猫狗识别
卑微小鹿
tensorflowtensorflow
由于猫和狗的数据在这里,所以就做了一下分类的神经网络1、首先进行图像处理:importcsvimportglobimportosimportrandomos.environ['TF_CPP_MIN_LOG_LEVEL']='2'importtensorflowastffromtensorflowimportkerasfromtensorflow.kerasimportlayersimportnum
- MATLAB车牌定位和识别系统
清风明月来几时
图像算法处理matlab开发语言
有很多方法可以实现MATLAB车牌的定位和识别系统。以下是一种可能的实现步骤:车牌定位:使用图像处理技术(如边缘检测、区域生长或颜色分割)来检测图像中的车牌区域。使用形态学操作来排除不符合车牌形状的区域。对车牌区域进行裁剪或调整大小,以便后续的识别。车牌识别:将车牌图像转换为灰度图像。使用图像处理技术(如二值化、滤波或增强)来减少噪音并突出字符。使用字符分割算法将车牌中的字符分开。使用特征提取方法
- MATLAB车牌识别系统
清风明月来几时
图像算法处理matlab开发语言
MATLAB车牌识别系统是一个基于MATLAB开发的用于识别和提取车牌信息的系统。该系统使用图像处理和机器学习算法来实现车牌的定位和字符识别。以下是一个基本的MATLAB车牌识别系统的工作流程:图像预处理:首先,将输入的图像进行预处理,包括灰度化、高斯平滑、边缘检测等操作,以提高后续的车牌定位和字符识别的准确性。车牌定位:在预处理后的图像中,使用形态学运算和边缘检测算法来寻找车牌的位置。这可以通过
- 直方图匹配(Histogram Matching)
姜太公钓鲸233
计算机视觉人工智能机器学习
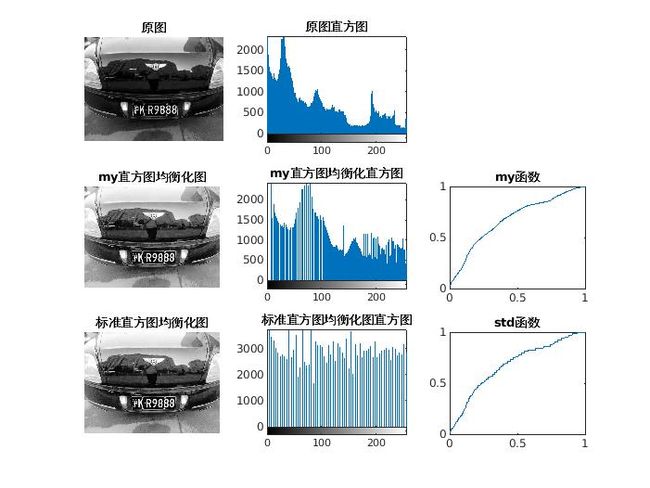
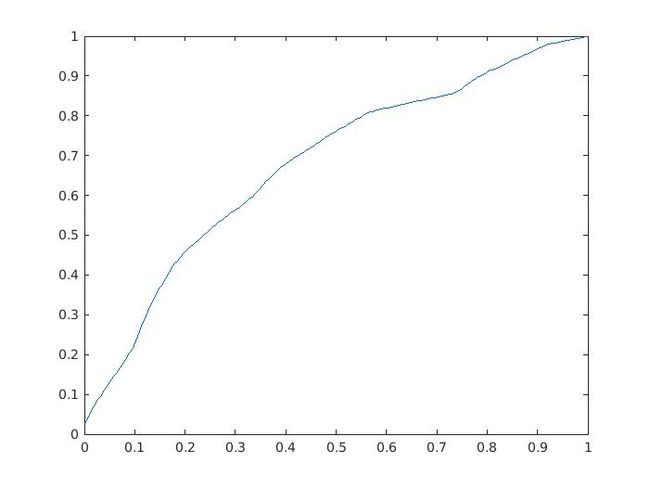
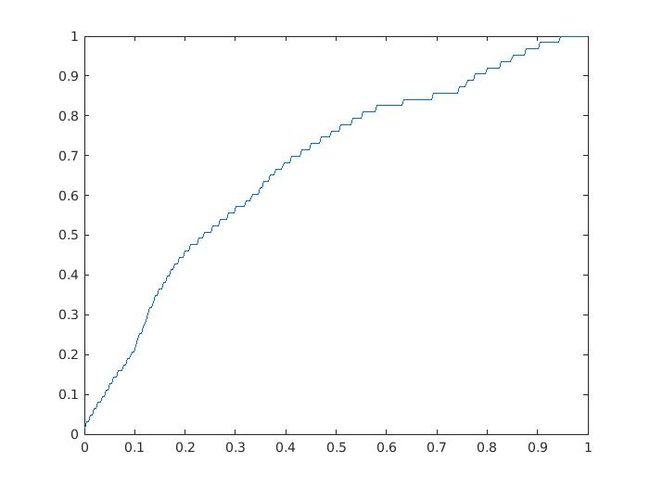
直方图匹配(HistogramMatching),也被称为直方图规定化(HistogramSpecification)或直方图修正(HistogramEqualization),是一种图像处理技术,用于调整图像的直方图,以使其与某个目标直方图相匹配。目标直方图通常是用户定义的或者是希望获得的期望分布。直方图匹配的目标是改变图像的像素值分布,从而使其在视觉上更接近目标直方图。这对于图像增强、风格迁移
- uint8
姜太公钓鲸233
pythonnumpy
无符号8位整数(uint8)是一种数据类型,通常用于表示整数,但它不包括负数,只能表示非负的整数值。它的范围是从0到255,共有256个不同的可能取值。在计算机中,整数数据类型可以分为有符号和无符号。有符号整数可以表示正数、负数和零,而无符号整数只能表示非负的整数。在图像处理中,无符号8位整数通常用于表示灰度图像的像素值。一个像素的灰度值代表了图像中对应点的亮度强度,通常从0(黑色)到255(白色
- 【Python第三方库】OpenCV库实用指南
墨辰JC
Pythonopencvpython人工智能学习
文章目录前言安装OpenCV读取图像图像基本操作获取图像信息裁剪图像图像缩放图像转换为灰度图图像模糊处理边缘检测图像翻转图像保存视频相关操作方法讲解读取视频从摄像头读取视频前言OpenCV(OpenSourceComputerVisionLibrary)作为一个强大的计算机视觉库,提供了丰富的图像处理和计算机视觉功能,尤其在图像识别、对象检测、视频分析等领域有着广泛的应用。本文将带领读者使用Pyt
- 计算机视觉之旅-进阶-图像滤波处理
撸码猿
计算机视觉图像处理人工智能
1.基本概念1.1.数字图像图像处理的对象是数字图像,它是由像素点阵列表示的图像。需要了解像素、图像分辨率、灰度级、RBG等图像表示方法。用numpy数组表示,每个元素为像素值。例如RGB图像 importnumpyasnp img=np.array([[[255,0,0],[0,255,0]],[[0,0,255],[255,255,255]]]) 1.2.采样和量化数字图像是通过采样和量化得到
- 动手学深度学习(pytorch土堆)-03常见的Transforms
#include<菜鸡>
深度学习深度学习pytorch人工智能
Composetransforms.Compose是PyTorch中的一个函数,用于将多个图像变换操作组合在一起,形成一个变换流水线。这样可以将一系列的图像处理操作整合为一个步骤,便于对图像进行批量预处理或增强。基本用法transforms.Compose接受一个列表,列表中的每个元素是一个变换操作。这些操作会按照给定的顺序依次作用在输入的图像上。Example:>>>transforms.Com
- 论文学习笔记 VMamba: Visual State Space Model
Wils0nEdwards
学习笔记
概览这篇论文的动机源于在计算机视觉领域设计计算高效的网络架构的持续需求。当前的视觉模型如卷积神经网络(CNNs)和视觉Transformer(ViTs)在处理大规模视觉任务时展现出良好的表现,但都存在各自的局限性。特别是,ViTs尽管在处理大规模数据上具有优势,但其自注意力机制的二次复杂度对高分辨率图像处理时的计算成本极高。因此,研究者希望通过引入新的架构来降低这种复杂度,并提高视觉任务的效率。现
- 数字图像处理(一系列对图像进行处理、分析和改进的技术)
编程日记✧
智能医疗计算机视觉图像处理人工智能
数字图像处理是指对图像进行一系列的数学和算法处理,以增强、分析或理解图像的内容。这些处理包括从基础的像素操作到复杂的高维变换和机器学习模型。1.图像降噪在图像获取和传输过程中,往往会引入噪声。降噪技术用于减少这些噪声,同时尽量保持图像的细节。常见方法有:均值滤波:将像素邻域内的像素值取平均值,从而平滑图像。这种方法简单但可能会模糊边缘。高斯滤波:使用高斯函数为权重对像素进行加权平均,可以更好地平滑
- python图像处理的图像几何变换
yava_free
图像处理python计算机视觉
一.图像几何变换图像几何变换不改变图像的像素值,在图像平面上进行像素变换。适当的几何变换可以最大程度地消除由于成像角度、透视关系乃至镜头自身原因所造成的几何失真所产生的负面影响。几何变换常常作为图像处理应用的预处理步骤,是图像归一化的核心工作之一[1]。一个几何变换需要两部分运算:空间变换:包括平移、缩放、旋转和正平行投影等,需要用它来表示输出图像与输入图像之间的像素映射关系。灰度插值算法:按照这
- OpenCV3最常用的基本操作
HeoLis
OpenCV介绍OpenCV的全称是OpenSourceComputerVisionLibrary,是一个跨平台的计算机视觉库。OpenCV是由英特尔公司发起并参与开发,以BSD许可证授权发行,可以在商业和研究领域中免费使用。OpenCV可用于开发实时的图像处理、计算机视觉以及模式识别程序。该程序库也可以使用英特尔公司的IPP进行加速处理。以上是维基百科关于OpenCV的介绍,简单来说它就是处理图
- yolov5 +gui界面+单目测距 实现对图片视频摄像头的测距
毕设宇航
QQ767172261yolov5单目测距
可实现对图片,视频,摄像头的检测项目概述本项目旨在实现一个集成了YOLOv5目标检测算法、图形用户界面(GUI)以及单目测距功能的系统。该系统能够对图片、视频或实时摄像头输入进行目标检测,并估算目标的距离。通过结合YOLOv5的强大检测能力和单目测距技术,系统能够在多种应用场景中提供高效、准确的目标检测和测距功能。技术栈YOLOv5:用于目标检测的深度学习模型。OpenCV:用于图像处理和单目测距
- Python中cv2 (OpenCV, opencv-python)库的安装、使用方法demo最新详细教程
猫头虎
AI人工智能技术专栏pythonopencv开发语言计算机视觉语音识别目标检测神经网络
Python中cv2(OpenCV,opencv-python)库的安装、使用方法demo最新详细教程文章目录Python中cv2(OpenCV,opencv-python)库的安装、使用方法demo最新详细教程摘要引言正文OpenCV库概述安装OpenCV环境要求安装命令验证安装基础使用方法读取和显示图像图像处理示例❓常见问题解答小结参考资料表格总结总结和未来展望温馨提示摘要本文全面介绍了Pyt
- c#视觉应用开发中如何使用Emgu CV在C#中进行图像处理?
openwin_top
C#视觉应用开发问题系列c#图像处理开发语言
microPythonPython最小内核源码解析NI-motion运动控制c语言示例代码解析python编程示例系列python编程示例系列二python的Web神器Streamlit如何应聘高薪职位EmguCV是OpenCV的.NET包装器,可以让开发者在.NET语言(如C#)中使用OpenCV的功能进行图像处理。在进行图像处理时,EmguCV提供了丰富的API可以使用。以下是使用EmguCV
- JVM StackMapTable 属性的作用及理解
lijingyao8206
jvm字节码Class文件StackMapTable
在Java 6版本之后JVM引入了栈图(Stack Map Table)概念。为了提高验证过程的效率,在字节码规范中添加了Stack Map Table属性,以下简称栈图,其方法的code属性中存储了局部变量和操作数的类型验证以及字节码的偏移量。也就是一个method需要且仅对应一个Stack Map Table。在Java 7版
- 回调函数调用方法
百合不是茶
java
最近在看大神写的代码时,.发现其中使用了很多的回调 ,以前只是在学习的时候经常用到 ,现在写个笔记 记录一下
代码很简单:
MainDemo :调用方法 得到方法的返回结果
- [时间机器]制造时间机器需要一些材料
comsci
制造
根据我的计算和推测,要完全实现制造一台时间机器,需要某些我们这个世界不存在的物质
和材料...
甚至可以这样说,这种材料和物质,我们在反应堆中也无法获得......
- 开口埋怨不如闭口做事
邓集海
邓集海 做人 做事 工作
“开口埋怨,不如闭口做事。”不是名人名言,而是一个普通父亲对儿子的训导。但是,因为这句训导,这位普通父亲却造就了一个名人儿子。这位普通父亲造就的名人儿子,叫张明正。 张明正出身贫寒,读书时成绩差,常挨老师批评。高中毕业,张明正连普通大学的分数线都没上。高考成绩出来后,平时开口怨这怨那的张明正,不从自身找原因,而是不停地埋怨自己家庭条件不好、埋怨父母没有给他创造良好的学习环境。
- jQuery插件开发全解析,类级别与对象级别开发
IT独行者
jquery开发插件 函数
jQuery插件的开发包括两种: 一种是类级别的插件开发,即给
jQuery添加新的全局函数,相当于给
jQuery类本身添加方法。
jQuery的全局函数就是属于
jQuery命名空间的函数,另一种是对象级别的插件开发,即给
jQuery对象添加方法。下面就两种函数的开发做详细的说明。
1
、类级别的插件开发 类级别的插件开发最直接的理解就是给jQuer
- Rome解析Rss
413277409
Rome解析Rss
import java.net.URL;
import java.util.List;
import org.junit.Test;
import com.sun.syndication.feed.synd.SyndCategory;
import com.sun.syndication.feed.synd.S
- RSA加密解密
无量
加密解密rsa
RSA加密解密代码
代码有待整理
package com.tongbanjie.commons.util;
import java.security.Key;
import java.security.KeyFactory;
import java.security.KeyPair;
import java.security.KeyPairGenerat
- linux 软件安装遇到的问题
aichenglong
linux遇到的问题ftp
1 ftp配置中遇到的问题
500 OOPS: cannot change directory
出现该问题的原因:是SELinux安装机制的问题.只要disable SELinux就可以了
修改方法:1 修改/etc/selinux/config 中SELINUX=disabled
2 source /etc
- 面试心得
alafqq
面试
最近面试了好几家公司。记录下;
支付宝,面试我的人胖胖的,看着人挺好的;博彦外包的职位,面试失败;
阿里金融,面试官人也挺和善,只不过我让他吐血了。。。
由于印象比较深,记录下;
1,自我介绍
2,说下八种基本类型;(算上string。楼主才答了3种,哈哈,string其实不是基本类型,是引用类型)
3,什么是包装类,包装类的优点;
4,平时看过什么书?NND,什么书都没看过。。照样
- java的多态性探讨
百合不是茶
java
java的多态性是指main方法在调用属性的时候类可以对这一属性做出反应的情况
//package 1;
class A{
public void test(){
System.out.println("A");
}
}
class D extends A{
public void test(){
S
- 网络编程基础篇之JavaScript-学习笔记
bijian1013
JavaScript
1.documentWrite
<html>
<head>
<script language="JavaScript">
document.write("这是电脑网络学校");
document.close();
</script>
</h
- 探索JUnit4扩展:深入Rule
bijian1013
JUnitRule单元测试
本文将进一步探究Rule的应用,展示如何使用Rule来替代@BeforeClass,@AfterClass,@Before和@After的功能。
在上一篇中提到,可以使用Rule替代现有的大部分Runner扩展,而且也不提倡对Runner中的withBefores(),withAfte
- [CSS]CSS浮动十五条规则
bit1129
css
这些浮动规则,主要是参考CSS权威指南关于浮动规则的总结,然后添加一些简单的例子以验证和理解这些规则。
1. 所有的页面元素都可以浮动 2. 一个元素浮动后,会成为块级元素,比如<span>,a, strong等都会变成块级元素 3.一个元素左浮动,会向最近的块级父元素的左上角移动,直到浮动元素的左外边界碰到块级父元素的左内边界;如果这个块级父元素已经有浮动元素停靠了
- 【Kafka六】Kafka Producer和Consumer多Broker、多Partition场景
bit1129
partition
0.Kafka服务器配置
3个broker
1个topic,6个partition,副本因子是2
2个consumer,每个consumer三个线程并发读取
1. Producer
package kafka.examples.multibrokers.producers;
import java.util.Properties;
import java.util.
- zabbix_agentd.conf配置文件详解
ronin47
zabbix 配置文件
Aliaskey的别名,例如 Alias=ttlsa.userid:vfs.file.regexp[/etc/passwd,^ttlsa:.:([0-9]+),,,,\1], 或者ttlsa的用户ID。你可以使用key:vfs.file.regexp[/etc/passwd,^ttlsa:.: ([0-9]+),,,,\1],也可以使用ttlsa.userid。备注: 别名不能重复,但是可以有多个
- java--19.用矩阵求Fibonacci数列的第N项
bylijinnan
fibonacci
参考了网上的思路,写了个Java版的:
public class Fibonacci {
final static int[] A={1,1,1,0};
public static void main(String[] args) {
int n=7;
for(int i=0;i<=n;i++){
int f=fibonac
- Netty源码学习-LengthFieldBasedFrameDecoder
bylijinnan
javanetty
先看看LengthFieldBasedFrameDecoder的官方API
http://docs.jboss.org/netty/3.1/api/org/jboss/netty/handler/codec/frame/LengthFieldBasedFrameDecoder.html
API举例说明了LengthFieldBasedFrameDecoder的解析机制,如下:
实
- AES加密解密
chicony
加密解密
AES加解密算法,使用Base64做转码以及辅助加密:
package com.wintv.common;
import javax.crypto.Cipher;
import javax.crypto.spec.IvParameterSpec;
import javax.crypto.spec.SecretKeySpec;
import sun.misc.BASE64Decod
- 文件编码格式转换
ctrain
编码格式
package com.test;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileOutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStream;
- mysql 在linux客户端插入数据中文乱码
daizj
mysql中文乱码
1、查看系统客户端,数据库,连接层的编码
查看方法: http://daizj.iteye.com/blog/2174993
进入mysql,通过如下命令查看数据库编码方式: mysql> show variables like 'character_set_%'; +--------------------------+------
- 好代码是廉价的代码
dcj3sjt126com
程序员读书
长久以来我一直主张:好代码是廉价的代码。
当我跟做开发的同事说出这话时,他们的第一反应是一种惊愕,然后是将近一个星期的嘲笑,把它当作一个笑话来讲。 当他们走近看我的表情、知道我是认真的时,才收敛一点。
当最初的惊愕消退后,他们会用一些这样的话来反驳: “好代码不廉价,好代码是采用经过数十年计算机科学研究和积累得出的最佳实践设计模式和方法论建立起来的精心制作的程序代码。”
我只
- Android网络请求库——android-async-http
dcj3sjt126com
android
在iOS开发中有大名鼎鼎的ASIHttpRequest库,用来处理网络请求操作,今天要介绍的是一个在Android上同样强大的网络请求库android-async-http,目前非常火的应用Instagram和Pinterest的Android版就是用的这个网络请求库。这个网络请求库是基于Apache HttpClient库之上的一个异步网络请求处理库,网络处理均基于Android的非UI线程,通
- ORACLE 复习笔记之SQL语句的优化
eksliang
SQL优化Oracle sql语句优化SQL语句的优化
转载请出自出处:http://eksliang.iteye.com/blog/2097999
SQL语句的优化总结如下
sql语句的优化可以按照如下六个步骤进行:
合理使用索引
避免或者简化排序
消除对大表的扫描
避免复杂的通配符匹配
调整子查询的性能
EXISTS和IN运算符
下面我就按照上面这六个步骤分别进行总结:
- 浅析:Android 嵌套滑动机制(NestedScrolling)
gg163
android移动开发滑动机制嵌套
谷歌在发布安卓 Lollipop版本之后,为了更好的用户体验,Google为Android的滑动机制提供了NestedScrolling特性
NestedScrolling的特性可以体现在哪里呢?<!--[if !supportLineBreakNewLine]--><!--[endif]-->
比如你使用了Toolbar,下面一个ScrollView,向上滚
- 使用hovertree菜单作为后台导航
hvt
JavaScriptjquery.nethovertreeasp.net
hovertree是一个jquery菜单插件,官方网址:http://keleyi.com/jq/hovertree/ ,可以登录该网址体验效果。
0.1.3版本:http://keleyi.com/jq/hovertree/demo/demo.0.1.3.htm
hovertree插件包含文件:
http://keleyi.com/jq/hovertree/css
- SVG 教程 (二)矩形
天梯梦
svg
SVG <rect> SVG Shapes
SVG有一些预定义的形状元素,可被开发者使用和操作:
矩形 <rect>
圆形 <circle>
椭圆 <ellipse>
线 <line>
折线 <polyline>
多边形 <polygon>
路径 <path>
- 一个简单的队列
luyulong
java数据结构队列
public class MyQueue {
private long[] arr;
private int front;
private int end;
// 有效数据的大小
private int elements;
public MyQueue() {
arr = new long[10];
elements = 0;
front
- 基础数据结构和算法九:Binary Search Tree
sunwinner
Algorithm
A binary search tree (BST) is a binary tree where each node has a Comparable key (and an associated value) and satisfies the restriction that the key in any node is larger than the keys in all
- 项目出现的一些问题和体会
Steven-Walker
DAOWebservlet
第一篇博客不知道要写点什么,就先来点近阶段的感悟吧。
这几天学了servlet和数据库等知识,就参照老方的视频写了一个简单的增删改查的,完成了最简单的一些功能,使用了三层架构。
dao层完成的是对数据库具体的功能实现,service层调用了dao层的实现方法,具体对servlet提供支持。
&
- 高手问答:Java老A带你全面提升Java单兵作战能力!
ITeye管理员
java
本期特邀《Java特种兵》作者:谢宇,CSDN论坛ID: xieyuooo 针对JAVA问题给予大家解答,欢迎网友积极提问,与专家一起讨论!
作者简介:
淘宝网资深Java工程师,CSDN超人气博主,人称“胖哥”。
CSDN博客地址:
http://blog.csdn.net/xieyuooo
作者在进入大学前是一个不折不扣的计算机白痴,曾经被人笑话过不懂鼠标是什么,