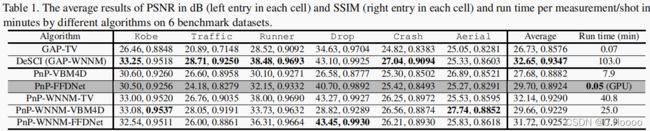
论文阅读——Plug-and-Play Algorithms for Large-scale Snapshot Compressive Imaging
大规模快照压缩成像的即插即用算法
- Abstract
- 1. Introduction
- 2. Mathematical Model of SCI
- 3. Plug-and-Play ADMM for SCI
-
- 3.1. Review the Plug-and-Play ADMM in [9]
- 3.2. PnP-ADMM for SCI
- 4. Plug-and-Play GAP for SCI
-
- 4.1. Algorithm
- 4.2. Fixed-point Convergence
- 4.3. Global Convergence of Plug-and-Play GAP
- 4.4. PnP-ADMM vs. PnP-GAP
- 5.将各种去噪器整合到PnP中进行SCI重建
Abstract
快照压缩成像(SCI)的目的是在单个快照中使用2D传感器(检测器)捕获高维(通常是3D)图像。虽然享受低带宽、低功耗和低成本的优势,但在日常生活中将SCI应用于大规模问题(高清或UHD视频)仍然具有挑战性。瓶颈在于重构算法;它们要么太慢(迭代优化算法),要么对编码过程(基于深度学习的端到端网络)不灵活。在本文中,我们开发了基于即插即用(PnP)框架的快速、灵活的SCI算法。除了广泛使用的PnP-ADMM方法外,我们还进一步提出了计算工作量较低的PnP-GAP(广义交替投影)算法,并证明了PnP-GAP在SCI硬件约束下的全局收敛性。通过采用深度去噪先验,我们首次证明了PnP可以从快照2D测量中恢复UHD彩色视频(3840×1644×48,PNSR超过30dB)。在仿真和真实数据集上的大量结果验证了我们提出的算法的优越性。
1. Introduction
计算成像的一个重要分支是快照压缩成像(SCI)[23,45],它利用一个二维(2D)相机来捕获3D视频或光谱数据。与传统相机不同的是,这种成像系统根据传感矩阵对一组连续的图像(如CACTI[23,60])或光谱通道(如CASSI[46])进行采样,并将这些采样信号沿时间或频谱进行集成,以获得最终的压缩测量值。通过这种技术,SCI系统[12,15,36,42,45,46,60]可以捕获高速运动[40,41,61,62,68,70]和高分辨率光谱信息[28,69,37],但具有低内存、低带宽、低功耗和潜在的低成本。在这项工作中,我们专注于视频SCI重建。
为了解决SCI重建的速度、准确性和灵活性三个问题,本文做出了以下贡献:
-
受ADMM框架的即插即用(PnP)交替方向方法的启发,我们将PnP-ADMM扩展到SCI,并通过考虑硬件约束和SCI中的感知矩阵[18]的特殊结构,证明了PnP-ADMM收敛到一个不动点。
-
我们提出了一种有效的PnP-GAP算法,通过在GAP中使用各种有界去噪器(图2),该算法的计算工作量比PnP-ADMM要低。除了不动点收敛外,我们还进一步证明了在适当的假设下,PnP-GAP的解将收敛于真信号。据我们所知,这是SCI的第一个全局收敛结果,这也适用于加性高斯白噪声下。

-
通过集成深度图像去噪,例如,快速和灵活的FFDNet到PnP-GAP,我们表明FHD视频(1920×1080×24)可以恢复从快照测量(图5)在2分钟内PSNR接近30dB使用一个GPU加上一个普通计算机。与端到端网络相比,节省了大量的资源(不需要再训练)。这进一步使得使用SCI进行UHD压缩成为可行的(图1中使用PSNR在30dB以上重建一个3840×1644×48视频)。据我们所知,这是SCI首次用于这些大规模问题。
-
我们将我们开发的PnP算法应用于广泛的模拟和真实的数据集(由真实的SCI相机捕获),以验证我们所提出的算法的效率和鲁棒性。我们表明,该算法可以获得与DeSCI相同的结果,但显著减少了计算时间。
2. Mathematical Model of SCI
如图1所示,在视频SCI系统中,考虑到B帧视频 X ∈ R n x × n y × B X∈R^{n_x×n_y\times B} X∈Rnx×ny×B被B个感知矩阵(掩模) C ∈ R n x × n y × B C∈R^{n_x×n_y\times B} C∈Rnx×ny×B调制和压缩,测量帧 Y ∈ R n x × n y Y∈R^{n_x×n_y} Y∈Rnx×ny可以表示为[23,60]:
Y = ∑ b = 1 B C b ⊙ X b + Z (1) \mathbf{Y}=\sum_{b=1}^{B}\mathbf{C_b}\odot\mathbf{X_b}+\mathbf{Z} \tag{1} Y=b=1∑BCb⊙Xb+Z(1)其中 Z ∈ R n x × n y Z∈R^{n_x×n_y} Z∈Rnx×ny表示噪声; C b = C ( : , : , b ) C_b=C(:,:,b) Cb=C(:,:,b)和 X b = X ( : , : , b ) ∈ R n x × n y X_b=X(:,:,b)∈R^{n_x×n_y} Xb=X(:,:,b)∈Rnx×ny代表第b个感知矩阵(掩码)和相应的视频帧。
在数学上,(1)中的测量值可以表示为
y = H x + z (2) \mathbf{y}=\mathbf{H}\mathbf{x}+\mathbf{z } \tag{2} y=Hx+z(2)其中 y = V e c ( y ) ∈ R n x n y , z = V e c ( Z ) ∈ R n x n y y=Vec(y)\in \mathbb{R^{n_xn_y}}\ ,z=Vec(Z)\in \mathbb{R^{n_xn_y}} y=Vec(y)∈Rnxny ,z=Vec(Z)∈Rnxny ,高光谱图像向量 x ∈ R n x n y B x∈\mathbb{R^{n_xn_yB}} x∈RnxnyB表示为
x = V e c ( X ) = [ V e c ( X 1 ) T , . . . , V e c ( X B ) T ] T (3) x=Vec(X)=[Vec(X_1)^T,...,Vec(X_B)^T]^T \tag{3} x=Vec(X)=[Vec(X1)T,...,Vec(XB)T]T(3)
与传统的压缩感知[5]不同,高光谱图像SCI中的感知矩阵 H ∈ R n x n y × n x n y B H∈R^{n_xn_y×n_xn_yB} H∈Rnxny×nxnyB并不是一个密集的矩阵。H的特殊结构可以表示为
H = [ D 1 , . . . , D B ] . (4) \mathbf{H}=[\mathbf{D_1},...,\mathbf{D_B}]. \tag{4} H=[D1,...,DB].(4)其中 D b = d i a g ( V e c ( C b ) ) ∈ R n × n , n = n x n y , b = 1 , . . . , B \mathbf{D}_b=diag(Vec(\mathbf{C}_b))\in \mathbb{R}^{n\times n},n=n_xn_y,b=1,...,B Db=diag(Vec(Cb))∈Rn×n,n=nxny,b=1,...,B. 由于 x ∈ R n x n y B \mathbf{x}\in \mathbb{R}^{n_xn_yB} x∈RnxnyB且 H ∈ R n x n y × n x n y B \mathbf{H}\in \mathbb{R}^{n_xn_y\times n_xn_yB} H∈Rnxny×nxnyB,SCI的采样率为1/B。[9,10]从理论上证明了当B>1时,x从y中恢复是可能的。
在彩色视频案例中,如图1、5和7,一般使用的拜耳(Bayer)模式传感器捕获的原始数据具有“RGGB”通道。由于掩模是施加在每个像素上的,生成的测量可以被视为如图6所示的灰度图像,当它以颜色显示时,由于掩模调制,脱色过程不能产生正确的颜色(图5)。因此,在重建过程中,我们首先独立恢复这四个通道,然后在重建的视频中进行除色。最终的RGB视频是所需的信号[60]。
3. Plug-and-Play ADMM for SCI
SCI的反演问题可以被建模为
x ^ = a r g m i n x f ( x ) + λ g ( x ) (5) \hat x=\mathop{argmin}\limits_{x}f(x)+\lambda g(x) \tag{5} x^=xargminf(x)+λg(x)(5)其中f(x)可以看作是正向成像模型的损失,即 ∣ ∣ y − H x ∣ ∣ 2 2 ||y−Hx||^2_2 ∣∣y−Hx∣∣22,g(x)是正则项。
3.1. Review the Plug-and-Play ADMM in [9]
通过使用ADMM框架[3],通过引入一个辅助参数v,即等式中的无约束优化(5)可以被转换为

这个最小化可以通过以下一系列的子问题来解决

而在SCI和其他反演问题中, f ( x ) f(x) f(x)通常是一种二次形式,对等式(7)有多种解,在PnP-ADMM中,等式(8)的解被一种现成的去噪算法所取代,即
v k + 1 = D σ ( x k + 1 ρ u k ) (10) v^{k+1}=D_\sigma (x^k+\frac{1}{\rho}u^k) \tag{10} vk+1=Dσ(xk+ρ1uk)(10)其中, D σ D_σ Dσ表示所使用的去噪器,σ为假设的加性高斯白噪声的标准差。在[9]中,作者提出使用 ρ k + 1 = γ k ρ k ρ_{k+1}=γ_kρ_k ρk+1=γkρk和 γ k ≥ 1 γ_k≥1 γk≥1在每次迭代中更新ρ并为去噪器设置 σ k = λ / ρ k σ_k=\sqrt {λ/ρ_k} σk=λ/ρk。由此定义了有界去噪器,并证明了PnP-ADMM的不动点收敛性。
Definition 1. 一个带有参数为σ的有界去噪器是一个函数 D σ : R n → R n D_σ:R^n→R^n Dσ:Rn→Rn,对于任何输入 x ∈ R n x∈R^n x∈Rn满足
1 n ∣ ∣ D σ ( x ) − x ∣ ∣ 2 ≤ σ 2 C , (11) \frac{1}{n}||D_\sigma(x)-x||^2\leq \sigma^2C, \tag{11} n1∣∣Dσ(x)−x∣∣2≤σ2C,(11)对于一个独立于n和σ的通用常数C。
有了这个定义(去噪约束)和 f : [ 0 , 1 ] n → R f:[0,1]^n→R f:[0,1]n→R的有界梯度,即对于任何 x ∈ [ 0 , 1 ] n x∈[0,1]^n x∈[0,1]n,存在 L < ∞ L<∞ L<∞,使得 ∣ ∣ ∇ f ( x ) ∣ ∣ 2 / n ≤ L ||∇f(x)||_2/\sqrt n≤L ∣∣∇f(x)∣∣2/n≤L.
[9]的作者已经证明了:PnP-ADMM的迭代证明了一个不动点收敛。即存在 ( x ∗ , v ∗ , u ∗ ) (x^∗,v^∗,u^∗) (x∗,v∗,u∗),使得当 k → ∞ k\to∞ k→∞时, ∣ ∣ x ( k ) − x ∗ ∣ ∣ 2 → 0 , ∣ ∣ v ( k ) − v ∗ ∣ ∣ 2 → 0 , ∣ ∣ u ( k ) − u ∗ ∣ ∣ 2 → 0 ||x^{(k)}-x^*||_2\to0,||v^{(k)}-v^*||_2\to0,||u^{(k)}-u^*||_2\to0 ∣∣x(k)−x∗∣∣2→0,∣∣v(k)−v∗∣∣2→0,∣∣u(k)−u∗∣∣2→0.
3.2. PnP-ADMM for SCI
在SCI中,使用在等式(2)中的模型, x ∈ R n B x∈R^{nB} x∈RnB,我们认为损失函数f(x)为 f ( x ) = 1 2 ∣ ∣ y − H x ∣ ∣ 2 2 (12) f(x)=\frac{1}{2}||y−Hx||^2_2 \tag{12} f(x)=21∣∣y−Hx∣∣22(12)考虑到所有的像素值都被归一化为[0,1]。

p r o o f : proof: proof:完整证明见补充材料(SM)。在这里,我们将给出关键步骤。 f ( x ) f(x) f(x)的梯度为 ∇ f ( x ) = H T H x − H T y , (13) \nabla f(x)=H^THx-H^Ty,\tag{13} ∇f(x)=HTHx−HTy,(13)其中H是等式(4)中定义的大小为 n × n B n×nB n×nB的块对角矩阵, H T y H^Ty HTy是非负的,因为测量y和掩模在本质上都是非负的,而 H T H x H^THx HTHx是x的加权和并且 ∣ ∣ H T H x ∣ ∣ 2 ≤ B C m a x ∣ ∣ x ∣ ∣ 2 ||H^THx||_2≤BC_{max}||x||_2 ∣∣HTHx∣∣2≤BCmax∣∣x∣∣2的加权和,其中 C m a x C_{max} Cmax是感知矩阵中的最大值。通常,感知矩阵被归一化为[0,1],这导致 C m a x = 1 C_{max}=1 Cmax=1,因此 ∣ ∣ H T H x ∣ ∣ 2 ≤ B ∣ ∣ x ∣ ∣ 2 ||H^THx||_2≤B||x||_2 ∣∣HTHx∣∣2≤B∣∣x∣∣2
此外,如果掩模元素 D i , j D_{i,j} Di,j是来自一个具有{0,1}的二进制分布, p 1 ∈ ( 0 , 1 ) p_1∈(0,1) p1∈(0,1)的概率为1,那么 ∣ ∣ H T H x ∣ ∣ 2 ≤ p 1 B ∣ ∣ x ∣ ∣ 2 ||H^THx||_2≤p_1B||x||_2 ∣∣HTHx∣∣2≤p1B∣∣x∣∣2的概率很高;通常, p 1 = 0.5 p_1=0.5 p1=0.5,因此有 ∣ ∣ H T H x ∣ ∣ 2 ≤ 0.5 B ∣ ∣ x ∣ ∣ 2 ||H^THx||_2≤0.5B||x||_2 ∣∣HTHx∣∣2≤0.5B∣∣x∣∣2。
∣ ∣ H T H x ∣ ∣ 2 ≤ B ∣ ∣ x ∣ ∣ 2 = σ = 1 B ∣ ∣ x ∣ ∣ 2 ||H^THx||_2≤B||x||_2\overset{σ=1}=B||x||_2 ∣∣HTHx∣∣2≤B∣∣x∣∣2=σ=1B∣∣x∣∣2在下面,我们只考虑非负掩模在实际系统中被归一化为[0,1]。
回想一下,在(4)中, { D i } i = 1 B \{D_i\}^B_{i=1} {Di}i=1B是一个对角矩阵,我们表示它的对角元素为
D i = d i a g ( D i , 1 , . . . , D i , n ) (14) D_i=diag(D_{i,1},...,D_{i,n})\tag{14} Di=diag(Di,1,...,Di,n)(14)因此,在SCI中, H H T HH^T HHT是对角线矩阵,即 R = H H T = d i a g ( R 1 , . . . , R n ) (15) \mathbf{R}=HH^T=diag(R_1,...,R_n)\tag{15} R=HHT=diag(R1,...,Rn)(15) Assumption 1. 假设 { R j } j = 1 n > 0 \{R_j\}^n_{j=1}>0 {Rj}j=1n>0。这意味着对于每个空间位置j,该位置上的b帧调制掩码至少有一个非零项,进一步假设 R m a x > R m i n R_{max}>R_{min} Rmax>Rmin。
Assumption 1. 假设 { R j } j = 1 n > 0 \{R_j\}^n_{j=1}>0 {Rj}j=1n>0。这意味着对于每个空间位置j,该位置上的b帧调制掩码至少有一个非零项,进一步假设 R m a x > R m i n R_{max}>R_{min} Rmax>Rmin。
这一假设在硬件中具有意义,因为我们预计在感知过程中,每个像素至少有一个B帧被捕获。引理1和定义1中的有界去噪器给出了下面的推论。
推论1. 考虑(2)中的SCI的感知模型,并进一步假设感知矩阵中的元素满足假设1。给定 { H , y } , x \{H,y\},x {H,y},x是通过具有有界去噪的PnP-ADMM迭代求解,则 x ( k ) x^{(k)} x(k)和 θ ( k ) θ^{(k)} θ(k)将收敛到一个不动点。
4. Plug-and-Play GAP for SCI
在本节中,根据GAP算法和上述关于PnP-ADMM的条件,我们提出了针对SCI的PnP-GAP,如前所述,它比PnP-ADMM具有更低的计算工作负载(因此更快)。
4.1. Algorithm
- Solving x x x:给定 v , x ( k + 1 ) v,x^{(k+1)} v,x(k+1)通过 v ( k ) v^{(k)} v(k)在线性流形 M : y = H x M:y=Hx M:y=Hx上的欧几里得投影进行更新
x ( k + 1 ) = v ( k ) + H T ( H H T ) − 1 ( y − H v ( k ) ) x^{(k+1)}=v^{(k)}+H^T(HH^T)^{-1}(y-Hv^{(k)}) x(k+1)=v(k)+HT(HHT)−1(y−Hv(k))如(15)中定义的, ( H H T ) − 1 (HH^T)^{−1} (HHT)−1是一个对角线矩阵,这已经被用于许多SCI反演问题。 - Solving v v v:给定 x x x,更新 v v v可以看作是一个去噪问题
v ( k + 1 ) = D σ ( x k + 1 ) (20) v^{(k+1)}=D_{\sigma}(x^{k+1}) \tag{20} v(k+1)=Dσ(xk+1)(20)这里,可以使用各种去噪器且 σ = λ σ=\sqrt λ σ=λ。
在每次迭代中,唯一需要调整的参数是 λ λ λ,因此我们将 ξ k ≤ 1 ξ_k≤1 ξk≤1设置为 λ k + 1 = ξ k λ k λ_{k+1}=ξ_kλ_k λk+1=ξkλk。受PnP-ADMM的启发,我们根据以下两条规则更新 λ λ λ: - a) 通过设置 λ k + 1 = ξ λ k λ_{k+1}=ξλ_k λk+1=ξλk与 ξ < 1 ξ<1 ξ<1单调更新;
- b) 通过考虑相对残差而进行的自适应更新:
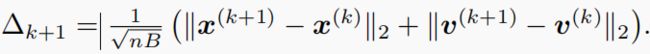
对于任何 η ∈ [ 0 , 1 ) η∈[0,1) η∈[0,1),并让ξ<1为一个常量, λ k λ_k λk将根据以下设置有条件地更新:
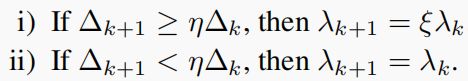
4.2. Fixed-point Convergence
下面,我们首先证明了PnP-GAP的不动点收敛性,然后在下一小节中证明了其全局收敛性。从等式开始(19),有
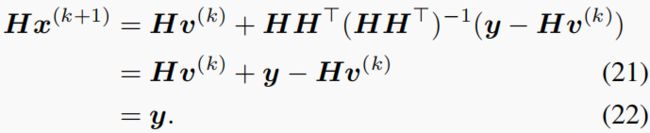
同样, y = H x ( k ) y=Hx^{(k)} y=Hx(k),这是GAP的关键属性,也是GAP和ADMM的主要区别。根据(19)有
![]()
由此可得

其中,最后两个方程遵循SM中引理1和2的结果。这就导致了下面的收敛结果。
Theorem 1. 考虑(2)中的SCI的感知模型,并进一步假设感知矩阵中的元素满足假设1。给定{H,y},x通过具有有界去噪器的PnP-GAP迭代求解,则 x ( k ) x^{(k)} x(k)和 v ( k ) v^{(k)} v(k)将收敛到一个不动点。
p r o o f : proof: proof:完整的证明是在SM中,它遵循了等式(26)和一个关键的结果是
∣ ∣ θ ( k + 1 ) − θ ( k ) ∣ ∣ 2 2 ≤ 7 n B C λ 0 ξ k − 1 (27) ||\theta^{(k+1)}-\theta^{(k)}||^2_2\leq7nBC\lambda_0\xi^{k-1}\tag{27} ∣∣θ(k+1)−θ(k)∣∣22≤7nBCλ0ξk−1(27)其中, θ ( k ) = ( x ( k ) , v ( k ) ) θ^{(k)}=(x^{(k)},v^{(k)}) θ(k)=(x(k),v(k)),其他步骤遵循推论1的证明。
Remark 1. 上述PnP-GAP的收敛结果也符合噪声测量结果。事实上,这个证明是与噪音无关的。这是因为 x ( k ) x^{(k)} x(k)的更新方程总是满足 y = H x ( k ) y=Hx^{(k)} y=Hx(k)。考虑噪声测量,即 y = H x ∗ + z y=Hx^∗+z y=Hx∗+z,其中 z ∈ R n z∈\mathbb{R}^n z∈Rn表示测量噪声。虽然这里的测量y与无噪声的情况不同,但我们仍然在每次迭代中强制执行 y = H x ( k ) y=Hx^{(k)} y=Hx(k)。
值得注意的是,我们已经证明了不动点的收敛性,但 x ( k ) x^{(k)} x(k)可能不收敛于真信号 x ∗ x^∗ x∗。我们证明了这种全局收敛可以在PnP-GAP中得到证明,而PnP-ADMM则具有挑战性。
4.3. Global Convergence of Plug-and-Play GAP
Assumption 2. 在SCI中,只有一个真实的信号 x ∗ x^∗ x∗满足测量模型 y = H x ∗ y=Hx^∗ y=Hx∗。
在实际情况下,可能有不止一个信号满足 y = H x y=Hx y=Hx,这个正向模型可能是物理成像系统的一个(线性)近似。利用这个假设,我们得到了以下PnP-GAP的全局收敛结果。
Theorem 2. [Global convergence of PnP-GAP] 考虑(2)中的SCI感知模型,并进一步假设感知矩阵中的元素满足假设1。考虑真正的信号 y = H x ∗ y=Hx^∗ y=Hx∗。在给定{H,y}的情况下,通过具有有界去噪器的PnP-GAP迭代求解 x ^ \hat x x^。对于一个恒定的 C g > 0 C_g>0 Cg>0和 0 < ϕ < 1 0<ϕ<1 0<ϕ<1.
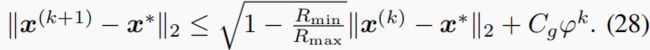
p r o o f : proof: proof: 从(19)开始,我们有

根据在(25)中的推导

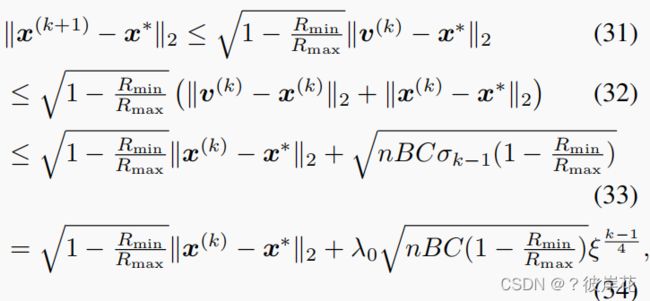
注意,由于 1 − R m i n R m a x < 1 \sqrt{1−\frac{R_{min}}{R_{max}}}<1 1−RmaxRmin<1和 ξ < 1 ξ<1 ξ<1,因此,当 k → ∞ k→∞ k→∞

在(28)中,定义
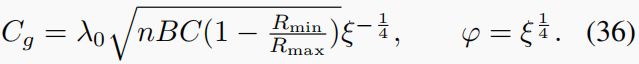
证毕。
注意,我们在假设1中假设了 R m i n < R m a x R_{min}
Theorem 3. [Stable convergence of PnP-GAP]考虑定理2中相同的条件,但现在的噪声测量 y = H x ∗ + z y=Hx^∗+z y=Hx∗+z和 ∣ ∣ z ∣ ∣ 2 ≤ ϵ ||z||_2≤\epsilon ∣∣z∣∣2≤ϵ。在给定{H,y}的情况下,通过具有有界去噪器的PnP-GAP迭代求解 x ^ \hat x x^。对于一个恒定的 C g > 0 C_g>0 Cg>0和 0 < ϕ < 1 0<ϕ<1 0<ϕ<1,

p r o o f : proof: proof: 与使用 y = H x ∗ y=Hx^∗ y=Hx∗的(29)不同,现在我们有(完整的细节在SM中)
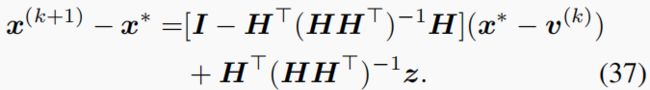
取两侧的 ℓ 2 ℓ_2 ℓ2范数,并利用(30)的一些推导结果,
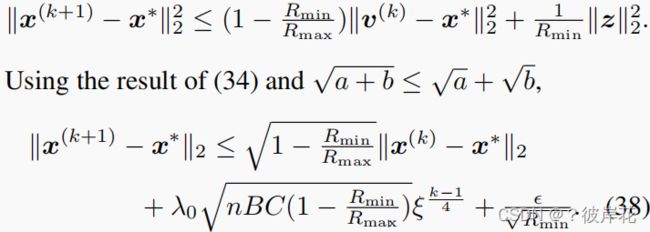
4.4. PnP-ADMM vs. PnP-GAP
通过比较(19)-(20)中的PnP-GAP和(7)-(9)中的PnP-ADMM,我们可以发现PnP-GAP只有两个子问题(而PnP-ADMM中的有三个子问题),因此计算速度更快。[22]指出,在无噪声情况下,ADMM和GAP的性能相同,并得到了数学证明。然而,在有噪声的情况下,ADMM通常表现得更好,因为它考虑了模型中的噪声,下面我们给出了一个几何解释。

如图所示,我们使用一个二维稀疏信号作为一个例子,我们可以看到,由于GAP强加 y = H x ^ y=H\hat x y=Hx^,GAP的解 x ^ \hat x x^总是在绿线(由于噪声,这条线可能会偏离实绿线真正的单一所在)。然而,ADMM的解没有这个约束,而是最小化 ∣ ∣ y − H x ∣ ∣ 2 2 ||y−Hx||^2_2 ∣∣y−Hx∣∣22,它可以根据初始化在红圆或黄色圆中。在无噪声的情况下,GAP和ADMM都将有很大的机会收敛到真信号 x ∗ x^∗ x∗。然而,在有噪声的情况下,GAP解与真信号之间的欧氏距离( ∣ ∣ x ^ − x ∗ ∣ ∣ 2 ||\hat x−x^∗||^2 ∣∣x^−x∗∣∣2)之间的欧氏距离可能大于ADMM。同样,ADMM的最终解决方案取决于初始化,它不能保证比GAP更准确。
5.将各种去噪器整合到PnP中进行SCI重建
从等式上就可以看到它定理2中的(28)重构误差项依赖于 C g ϕ k C_gϕ_k Cgϕk,从(35)中观察到 { n , B , R m i n , R m a x } \{n,B,R_{min},R_{max}\} {n,B,Rmin,Rmax}是固定的, { λ 0 , ξ } \{λ_0,ξ\} {λ0,ξ}是预设或调整的,只有C依赖于有界去噪算法。换句话说,一个更好的去噪器和一个较小的C可以提供一个更接近真实信号的重建结果。基于速度和质量的不同任务存在不同的去噪算法。通常,一个更快的去噪器,如TV,是非常有效的,但不能提供高质量的结果。中级的算法,例如BM3D[10],可以以较长的运行时间提供良好的结果。更先进的去噪算法,例如,WNNM[14,13]可以提供更好的结果,[22],但甚至更慢。另一种新兴的去噪方法是基于深度学习[48,73],它可以在训练后的短时间内提供良好的结果,但它们通常对噪声水平不鲁棒,在高噪声情况下,结果并不好。与传统的去噪问题不同,在SCI重建中,每次迭代的噪声水平通常从大到小,动态范围可以从150到1,考虑到像素值在{0,1,…,255}。幸运的是,FFDNet[74]为我们提供了一个在不同噪声水平下快速、灵活的解决方案。
通过将这些去噪算法集成到PnPGAP/ADMM中,我们可以得到不同的算法(表1和图2),并得到不同的结果。值得注意的是,DeSCI可以看作是PnP-WNNM,利用不同视频帧间的相关性可以取得最佳效果。另一方面,大多数现有的深度去噪先验仍然是基于图像的。因此,预计PnP-GAP/ADMM-FFDNet的结果不如DeSCI好。我们预计,随着深度去噪先验的进步,更好的视频去噪方法将提高我们基于pnp的SCI重建结果。此外,这些不同的去噪器可以并行使用,即在一个GAP/ADMM迭代中相互使用或依次使用,即使用FFDNet的第一次K1迭代和使用WNNM的第二次K2迭代,以获得更好的结果。