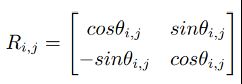论文浅尝 | 基于正交普鲁克分析的高效知识图嵌入学习
笔记整理:朱渝珊,浙江大学在读博士,研究方向为快速知识图谱的表示学习,多模态知识图谱。
1.Motivation
知识图谱是许多NLP任务和下游应用的核心,如问答、对话代理、搜索引擎和推荐系统。知识图中存储的事实总是以元组的形式存在,元组由一个头实体、一个尾实体(都是知识图中的节点)和它们之间的关系(知识图中的边)组成。KGEs学习知识图中关系和实体的表示,然后用于下游任务,如预测缺失的关系。深度学习的应用使KGE取得了重大进展。尽管如此,这些方法在计算上是昂贵的,并伴随着相当大的环境成本。
为了降低计算成本,作者引入了PROCRUSTES,一种轻量级、快速、环保的KGE训练技术。PROCRUSTES建立在三种新技术之上。首先,为了减少批量学习的计算开销,作者提出通过对元组之间的关系进行分组来实现批量并行化,最终实现高效的全批量学习。其次,作者转向正交普鲁克问题的一个封闭解来促进嵌入训练,这在KGEs环境中从未被探索过。第三,为了突破带宽瓶颈,该算法允许在没有负样本的情况下进行训练。本文的主要贡献有:
1.引入了三种新的方法来大幅减少嵌入大型复杂知识图的计算开销:基于关系矩阵的全批学习,KGEs的封闭形式正交普鲁克分析,以及非负抽样训练;2.在两个标准数据集上对13个强基线进行了系统的基准测试,结果表明该算法在几分钟的训练时间和很少碳排放情况下保持了极具竞争力的性能;3.首次将实体信息和关系信息同时编码到单个向量空间中,丰富了实体嵌入的表达性,并对可解释性产生了新的见解。
2.Method
2.1基础(分段embedding)
PROCRUSTES模型是建立在分段嵌入的基础上的,这种技术已经被一些很有前途的KGE学习方法(如RotatE, SEEK,OTE)利用。与传统的KGEs方法中每个实体只对应一个向量不同,采用分段嵌入的算法显式地将实体表示空间划分为多个独立的子空间。在训练期间,每个实体被编码为一串解耦的子向量(即不同的段,因此得名)。例如,如Figure 1所示,对一个包含7个实体的图进行编码,第t个实体的嵌入是其d/ds个子向量的逐行拼接,其中d和ds分别表示实体向量和子向量的维数。采用分段嵌入允许并行处理结构上分离的子空间,从而显著提高整体训练速度。此外,分割嵌入还可以增强模型的整体表现力,同时大大减少矩阵计算的维数。
2.2通过关系矩阵进行全批学习
分段嵌入通过并行化元组计算来提高训练速度。本节提出了一种基于关系矩阵的全批学习技术,它可以优化批计算,从而进一步减少训练时间。这个想法的动机是观察到现有的神经KGE框架都是基于由不同类型关系组成的元组构造的随机批次进行训练。这种训练模式是基于随机批处理的,虽然实现起来很简单,但很难并行化。这是由于计算机进程调度的本质:在进程读取和更新关系嵌入之间的间隔期间,它们很可能被其他进程修改,导致同步错误,从而导致意外的数据损坏,降低优化,甚至收敛问题。
为了解决这个问题,作者提出通过将包含相同关系的元组分组来构造训练批次。组这种新策略的优势是双重的。首先,它自然地将原始的元级计算简化为简单的矩阵级算术。更重要的是,这样可以轻松地确保每个关系的嵌入只能被单个进程访问,完全避免了数据损坏问题。此外,它使全批学习技术(通过关系矩阵)的使用成为可能,为KGEs训练过程的并行化提供了一个鲁棒的解决方案,从而大大提高了训练速度。这是KGE社区首次探索这种方法。
如Figure 1,首先将嵌入空间分割成段,并根据关系来排列批次。然后,对于每个训练步,PROCRUSTES的工作流本质上被分解为m × (d/ds)个并行过程,m为关系数。设i表示关系id,j是子空间索引,所以关系i的所有三元组的头实体的第j个子空间向量的列联合可表示为H_(i,j),所有三元组的尾实体的第j个子空间向量的列联合可表示为T_(i,j)。关系i的第j个子空间向量表示为R_(i,j)。最后的目标函数为:
2.3正交普鲁克分析
作者仿照RotatE和OTE等工作,希望限制关系矩阵R_(i,j)是正交的。很多KGE工作用不同的方式限制正交性,例如RotatE利用欧拉定理并定义关系嵌入为公式
其中θ_(i,j) 是可学习的参数。尽管上述公式保持了正交性和简单性,它本质上是一个ds=2的分段嵌入,但是R_(i,j)始终只有两维,这限制了模型能力。为了克服这个问题,OTE在每个反向传播步骤中使用Gram-Schmidt算法显式地正交化R_(i,j) (详见附录)。然而,虽然这种方案适用于各种ds的范围(即子空间向量的维度),但这在计算上非常昂贵。
作者利用所提出的全批学习的可并行性来解决计算问题。与现有处理异构关系的方法相比,PROCRUSTES在全批学习中,在每个过程中只需要优化一个R_(i,j),这是一个简单的约束矩阵回归任务。更重要的是,通过奇异值分解(SVD),可以得到一个封闭的解:
其中R_(i,j)^*是最适条件,在每次迭代中,PROCRUSTES可以在给定当前实体嵌入的情况下,应用上述公式找到每个关系的最优嵌入。然后,基于目标函数,PROCRUSTES再通过反向传播更新实体的嵌入(关系嵌入不需要梯度)。以上过程不断重复直到收敛。
由于关系嵌入的优化几乎可以在每次迭代中立即完成, PROCRUSTES比RotatE和OTE快很多数量级。此外,相比其他KGE模型用实体嵌入更新独立的关系嵌入,PROCRUSTES训练的实体嵌入可以直接用于恢复关系嵌入(通过上述封闭解),这表明PROCRUSTES可以在实体空间中编码更丰富的信息。
2.4进一步的优化策略:非负采样机制
现有的KGE方法采用负采样作为减少训练时间的标准技术,但是根据生成的负样本计算损失,仅对参数的子集进行了更新。通过作者提出的封闭式解决方案,计算梯度来更新嵌入不再是PROCRUSTES的效率瓶颈。相反,速度瓶颈是由于增加的负样本所占用的额外带宽。因此,对于PROCRUSTES,作者提出不采用负采样,而是在每一轮反向传播中只使用正样本更新所有嵌入,以进一步优化训练速度(附录显示了与采用负采样的基线的带宽比较)。
但是,如果不采用任何额外限制,在训练中PROCRUSTES会陷入一个平凡最优,即L=0,此时所有的H_(i,j),T_(i,j)和R_(i,j)都是0。换句话说,这个模型完全没有编码。这在某种程度上并不奇怪,因为这种平凡最优往往会产生较大的梯度,从而导致这种结果。为了缓解这一退化问题,受到正交R_(i,j)的几何意义的启发(即,围绕坐标原点向T_(i,j)方向旋转H_(i,j),而不改变矢量长度),作者提出通过在每个epoch执行两个步骤来约束所有实体到一个高维超球体:1)centering,分别转换H_(i,j)和T_(i,j),使每个矩阵的列和为0向量(每行表示一个实体的子空间向量);2)length normalization,确保H_(i,j)和T_(i,j)的行欧几里德范数是1。
3.Experiment
3.1数据集、基线与指标
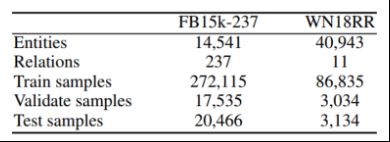
3.1.1数据集
3.1.2Baseline
经典的TransE, DistMult, ComplEx, 以及在WN18RR和FB15k237数据集上达到最佳性能的R-GCN, ConvE, A2N, RotatE, SCAN, TuckER, QuatE, InteractE, OTE, RotH。
3.1.3评估指标
评估指标包含MRR和Hit@1、3、10。在效率方面,对比每个模型消耗的时间和二氧化碳排放量(从开始训练到收敛)。
3.1.4实验细节
模型的关键超参数是d和ds,两个数据集的超参数分别设置为2K和20。每个模型进行最多2K个epoch的训练,并每100个epoch之后验证MRR是否停止增加。对于WN18RR和FB15k-237,作者报告的最佳超参数分别为固定学习率0.001和0.05 (Adam optimizer)。
3.2实验结果
从实验结果中可以看出本文提出的方法相较于多数现有的KGE方法在链接预测上有明显提升,并且具有很快的训练速度和低碳排放量。
3.3不同维度的影响
实验还表明,超参数d和ds的选择对PROCRUSTES的有效性和效率有重要影响。对于整个嵌入空间的维数,固定ds=20,设置d={100;200;400;800;1k;1:5K;2K},结果如下图所示。随着d的增加,性能(MRR)增加,但训练时间也随之增加。训练时间的曲率在d>1K时几乎饱和,作者以d=2K作为WN18RR和FB15k-237的最佳设置。
对于子空间嵌入的维数,固定d=2K,设置ds={2;5;10;20;25;50;100}。在ds达到20或25之前,模型性能快速提升,但之后随着网络学习能力的降低,模型缓慢退化。巧合的是,当ds=20时,训练速度也达到了顶峰,作者以ds=20作为WN18RR和FB15k-237的最佳设置。
3.4解释实体嵌入
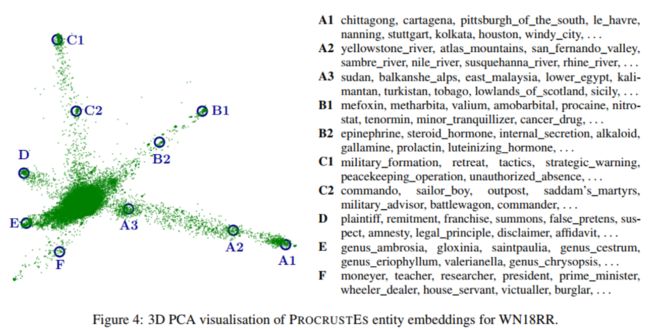
作者对训练的实体嵌入进行可视化,即使用主成分分析PCA对嵌入进行降维,将实体嵌入的维数从2K降为3,下图显示了可视化结果,从中我们可以看到一个有6个“手臂”的图表。首先,同一臂上的实体在语义上是相似的,或者说这些实体属于同一个类别。具体来说,A臂上的实体是位置,B臂上的实体是生化术语,C臂上的实体是军事相关的实体。D、E、F臂上的实体分别是指法律概念、植物学概念和职业概念。第二,手臂上的每个簇/位置之间存在显著差异:对于A臂,A1是城市的实体,如斯图加特、休斯顿、南宁;A2是关于河流、山脉等实体的;A3为国家或地区实体。同样,B1主要由医药名称组成,B2中的实体明显与化学术语有关。
4.Summery
本文提出了一种新的KGE训练框架,PROCRUSTES,它是环保的、高效的,可以产生非常有竞争力甚至接近最先进的性能。大量实验表明,该方法是有价值的,特别是它能够显著地减少训练时间和碳排放。
欢迎有兴趣的同学阅读原文。
OpenKG
OpenKG(中文开放知识图谱)旨在推动以中文为核心的知识图谱数据的开放、互联及众包,并促进知识图谱算法、工具及平台的开源开放。
点击阅读原文,进入 OpenKG 网站。