python数据结构和算法

前面系统地学习了python相关的基础知识，接下来，我们将继续学习python的数据结构和算法。 

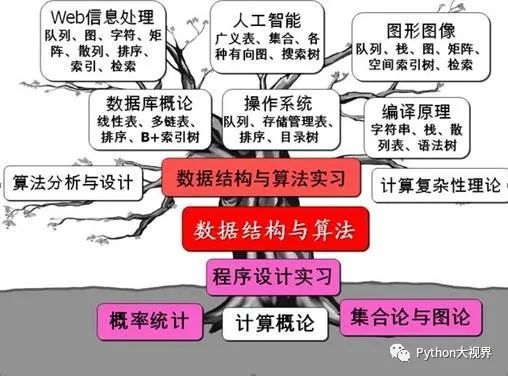
我们知道，程序=数据结构+算法，那么，什么是数据结构，有什么是算法呢？如何系统的学习数据结构和算法呢？数据结构和算法在计算机世界中的作用如下图所示：

Part.1  为什么要学习数据结构和算法？

遇到一个实际问题，需要解决两个事情：

（1）问题涉及到哪些数据信息；

（2） 用什么方法策略解决问题。

前者是数据结构，后者是算法。数据是一切能输入到计算机的信息总和，结构是指数据之间的关系，数据结构就是将数据及其之间的关系有效地存储在计算机中。如何将数据中的问题存储到计算机中，使其变得可用，成为有组织有效的可用信息，即为数据结构的任务。数据结构由逻辑结构，存储结构和运算三部分组成。

当面对问题时，如何解决，即解决方法和步骤，即为算法。算法是指对特定问题求解步骤的一种描述，说白了就是解决问题的方法策略。算法是整个程序的灵魂，我们在处理问题时，算法就是解空间和问题空间的桥梁。

遇到一个实际问题，充分利用所学的数据结构，将数据及其之间的关系有效地存储在计算机中，然后选择合适的算法策略，并用程序高效实现。这就是N.Wirth教授所说的：数据结构+算法＝程序。

以编程为例：
 编程好比是一辆汽车，而数据结构和算法是汽车内部的变速箱。一个开车的人不懂变速箱的原理也是能开车的，同理一个不懂数据结构和算法的人也能编程。但是如果一个开车的人懂变速箱的原理，比如降低速度来获得更大的牵引力，或者通过降低牵引力来获得更快的行驶速度。那么爬坡时使用1档，便可以获得更大的牵引力；下坡时便使用低档限制车的行驶速度。

回到编程而言，比如将一个班级的学生名字要临时存储在内存中，你会选择什么数据结构来存储，数组还是ArrayList，或者HashSet，或者别的数据结构。如果不懂数据结构的，可能随便选择一个容器来存储，也能完成所有的功能，但是后期如果随着学生数据量的增多，随便选择的数据结构肯定会存在性能问题，而一个懂数据结构和算法的人，在实际编程中会选择适当的数据结构来解决相应的问题，会极大的提高程序的性能 。  

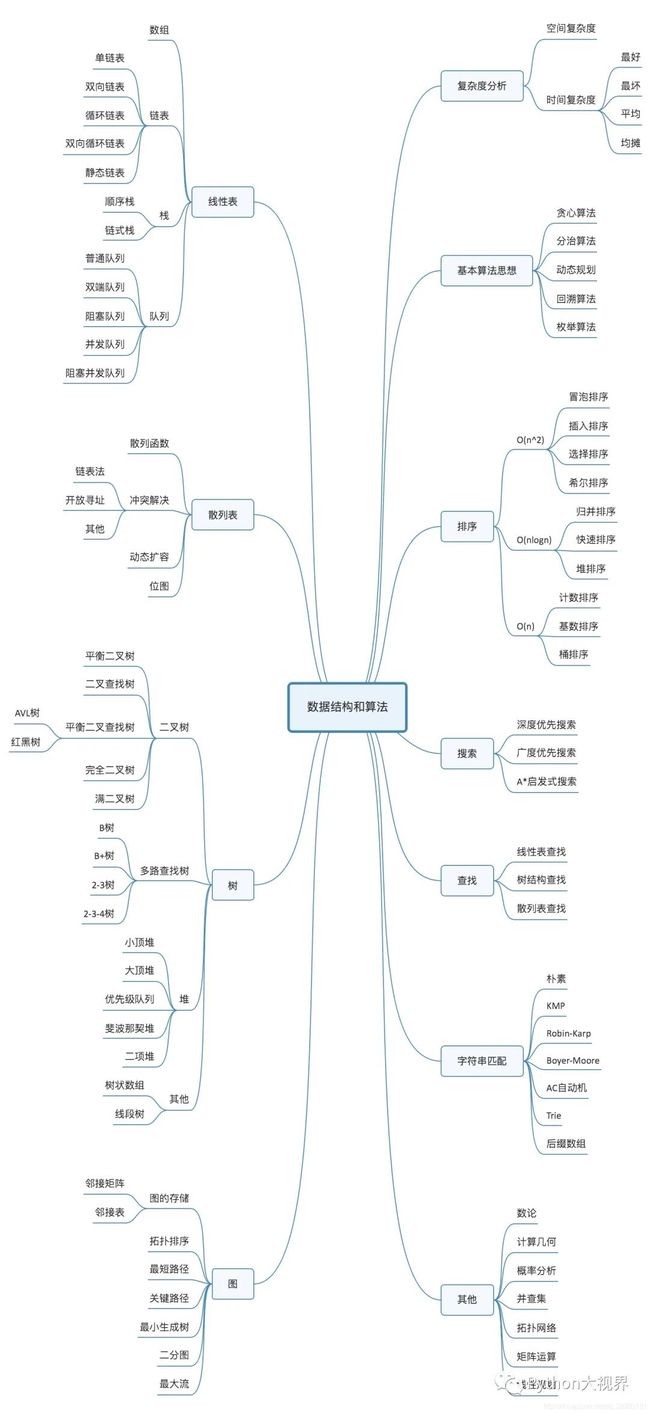
数据结构和算法知识体系如下：

Part.2  数据结构简介

  通常而言， 数据结构由以下三部分组成，数据结构=逻辑结构+存储结构+增删改查，

数据结构分为线性结构和非线性结构，常见的线性结构有：数组、队列、链表、栈。非线性结构有：二维数组、多维数组、广义表、树结构、图结构。

 但凡涉及到数据，均会考虑数据的操作，即增删改查，

　　①、如何插入一条新的数据项

　　②、如何寻找某一特定的数据项

　　③、如何删除某一特定的数据项

　　④、如何迭代的访问各个数据项，以便进行显示或其他操作

而操作的时间复杂度和空间复杂度是我们考虑使用何种的数据结构的考虑标准之一。

常见数据结构优缺点比较：

Part.3 算法简介

算法，顾名思义，即为解决问题的步骤，算法的特征包括有穷性，确定性，可行性，有输入，有输出。

算法的五个特征

　　1，有穷性：对于任意一组合法输入值，在执行又穷步骤之后一定能结束，即：算法中的每个步骤都能在有限时间内完成。

　　2，确定性：在每种情况下所应执行的操作，在算法中都有确切的规定，使算法的执行者或阅读者都能明确其含义及如何执行。并且在任何条件下，算法都只有一条执行路径。

　　3，可行性：算法中的所有操作都必须足够基本，都可以通过已经实现的基本操作运算有限次实现之。

　　4，有输入：作为算法加工对象的量值，通常体现在算法当中的一组变量。有些输入量需要在算法执行的过程中输入，而有的算法表面上可以没有输入，实际上已被嵌入算法之中。

　　5，有输出：它是一组与“输入”有确定关系的量值，是算法进行信息加工后得到的结果，这种确定关系即为算法功能。

那么，面对不同问题的解决方法和同一问题的不同方法之间，应该怎么去衡量算法的好坏呢？比如说我们计算从1+2+3+、、、、+100，这个用python如何实现呢？

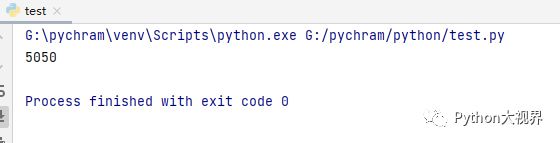
sum=0for i in range(1,101):    sum+=iprint ( sum )

上述代码中，我们直接计算从1加到100，计算结果如下：

那么，如果用高斯计算方法呢？即（1+100）*50，具体代码如下​​​​​​​

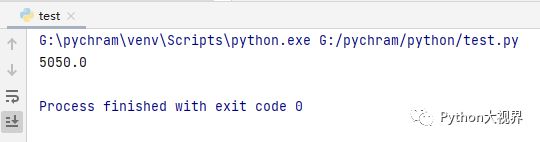
def SUM(n):    return n*(n+1)/2getRel=SUM(100)print(getRel)

结果如下：

那么，如何去评价这两个算法的好坏呢？

衡量算法优越性的三个尺度：空间复杂度，时间复杂度，及稳定性。

空间复杂度：一句来理解就是，此算法在规模为n的情况下额外消耗的储存空间。

时间复杂度：一句来理解就是，此算法在规模为n的情况下，一个算法中的语句执行次数称为语句频度或时间频度。

稳定性：主要是来描述算法，每次执行完，得到的结果都是一样的，但是可以不同的顺序输入，可能消耗的时间复杂度和空间复杂度不一样。

通常，我们用执行时间的长短来比较算法的好坏，即利用时间复杂度来衡量算法。在算法中，我们对时间复杂度的定义如下：

时间复杂度：假设存在函数g，使得算法A处理规模为n的问题示例所用时间为T(n)=O(g(n))，则称O(g(n))为算法A的渐近时间复杂度，简称时间复杂度，记为T(n)

在实际中，我们用大O来表示算法的时间效率：

“大O记法”：对于单调的整数函数f，如果存在一个整数函数g和实常数c>0，使得对于充分大的n总有f(n)<=c*g(n)，就说函数g是f的一个渐近函数（忽略常数），记为f(n)=O(g(n))。也就是说，在趋向无穷的极限意义下，函数f的增长速度受到函数g的约束，亦即函数f与函数g的特征相似。

如何理解大O记法呢？对于算法的时间性质和空间性质，最重要的是其趋势和数量级，比如说，两个时间复杂度为3n^3 和100n^3的算法，当n值非常大时，前面的系数可近似忽略，则他们的时间复杂度近似为O（n^3），

判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度。

时间复杂度几个常见的规则：

基本操作，即只有常数项，认为其时间复杂度为O(1)

顺序结构，时间复杂度按加法进行计算

循环结构，时间复杂度按乘法进行计算

分支结构，时间复杂度取最大值

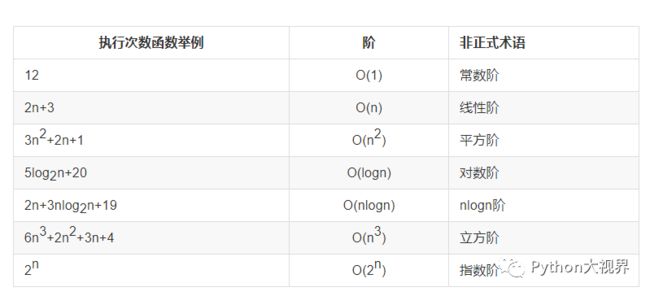
常见的时间复杂度如下；

相互关系比较如下：

从上图可以看出，时间复杂度从小到大依次是
O(1) < O(logn) 

我们用一个例子来理解时间复杂度：

如果 a+b+c=1000，且 a^2+b^2=c^2（a,b,c 为自然数），如何求出所有a、b、c可能的组合?
第一种解法：我们从1到1000遍历a,b,c，如果他们的满足a+b+c=1000,且a^2+b^2=c^2,则打印a,b,c,代码如下：​​​​​​​

import timestart_time=time.time()for a in range(0,1001):    for b in range(0,1001):        for c in range(0,1001):            if a+b+c==1000 and a**2+b**2==c**2:                print ( "a, b, c: %d, %d, %d" % (a , b , c) )end_time = time.time()print("elapsed: %f" % (end_time - start_time))print("complete!")

上述代码的时间复杂度为：O(n^3)运行结果如下：

如果换一种方法去实现，则​​​​​​​

import timestart_time=time.time()for a in range(0,1001):    for b in range(0,1000-a):        c=1000-a-b        if a**2+b**2==c**2:            print ( "a, b, c: %d, %d, %d" % (a , b , c) )end_time = time.time()print("elapsed: %f" % (end_time - start_time))print("complete!")

上述代码的复杂度为O(n^2),运行结果如下：

针对于同一个问题，两种不同的算法，第一种时间为188.26s 第二种时间为 0.664s，可见算法的设计不同，时间复杂度也大不相同。