【sklearn学习】逻辑回归LogisticRegression
逻辑回归的优点:
- 使用于分类问题中的回归算法
- 逻辑回归对线性关系的拟合效果好
- 逻辑回归计算快
- 逻辑回归返回的分类结果不固定,而是以小数的形式呈现的类概率数字
- 逻辑回归有抗噪能力强的特点,在小数据集上表现较好
sklearn.linear_model.LogisticRegression
class sklearn.linear_model.LogisticRegression(penalty='l2', *, dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver='lbfgs', max_iter=100, multi_class='auto', verbose=0, warm_start=False, n_jobs=None, l1_ratio=None)
penalty:字符串,指定正则化策略,'l1'或'l2'
dual:bool,默认为True,求解对偶形式
C:float,指定惩罚项系数的倒数,如果值越小,则正则化项越大
fit_intercept:bool,是否需要计算b值
intercept_scaling:float,只有当solver='liblinear'才有意义
使用损失函数衡量参数为θ的模型拟合训练集时产生的信息损失的大小,并以此衡量参数θ的优劣
在模型拟合过程中,让损失函数最小化的参数组合
正则化用来防止模型过拟合,常用的有L1正则化和L2正则化
L1范式表示每个参数的绝对值之和
L2范式表示为参数向量中的每个参数的平方和的开方值
L1正则化会将参数压缩到0,L2正则化只会让参数尽量小,不会取到0
导入常用的包:
import matplotlib as plt
import pandas as pd
from sklearn.datasets import load_breast_cancer, load_wine
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split二分类问题代码实现:
cancer = load_breast_cancer()
df_data = pd.DataFrame(cancer.data)
df_data.columns = cancer.feature_names
df_target = pd.DataFrame(cancer.target)
df_target.columns = ['LABEL']
df = pd.concat([df_data, df_target], axis=1)X_train, X_test, y_train, y_test = train_test_split(df_data, df_target['LABEL'], test_size=0.2, random_state=0)
lr = LogisticRegression(max_iter=600, solver='liblinear', random_state=0)
lr.fit(X_train, y_train)
train_score = lr.score(X_train, y_train)
print("train score:", train_score)
test_score = lr.score(X_test, y_test)
print("test score:", test_score)k折交叉验证:
from sklearn.model_selection import KFold
from sklearn.metrics import accuracy_score
data_train, data_test, target_train, target_test = train_test_split(df_data, df_target['LABEL'], test_size=0.2, random_state=0)
folds = KFold(n_splits=10)
train_scores = 0
val_scores = 0
for fold, (train_index, val_index) in enumerate(folds.split(data_train, target_train)):
print("fold {}".format(fold+1))
X_train, X_val, y_train, y_val = data_train.values[train_index],data_train.values[val_index],target_train.values[train_index],target_train.values[val_index]
clf = LogisticRegression(max_iter=10000, solver='lbfgs')
clf.fit(X_train,y_train)
pred_train = clf.predict(X_train)
pred_val = clf.predict(X_val)
train_score = accuracy_score(pred_train, y_train)
val_score = accuracy_score(pred_val, y_val)
train_scores += train_score
val_scores += val_score
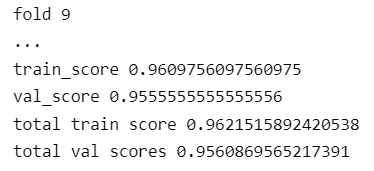
print('train_score',train_score)
print('val_score',val_score)
print("total train score",train_scores/10)
print("total val scores",val_scores/10)
多分类问题代码实现:
wine = load_wine()
df_data = pd.DataFrame(wine.data)
df_data.columns = wine.feature_names
df_target = pd.DataFrame(wine.target)
df_target.columns = ['LABEL']
df = pd.concat([df_data, df_target], axis=1)X_train, X_test, y_train, y_test = train_test_split(df_data, df_target['LABEL'], test_size=0.2, random_state=0)
lr = LogisticRegression(max_iter=3000, multi_class='multinomial',solver='lbfgs')
lr.fit(X_train, y_train)
train_score = lr.score(X_train, y_train)
print("train score:", train_score)
test_score = lr.score(X_test, y_test)
print("test score:", test_score)from sklearn.model_selection import KFold
from sklearn.metrics import accuracy_score
data_train, data_test, target_train, target_test = train_test_split(df_data, df_target['LABEL'], test_size=0.2, random_state=0)
folds = KFold(n_splits=10)
train_scores = 0
val_scores = 0
for fold, (train_index, val_index) in enumerate(folds.split(data_train, target_train)):
print("fold {}".format(fold+1))
X_train, X_val, y_train, y_val = data_train.values[train_index],data_train.values[val_index],target_train.values[train_index],target_train.values[val_index]
clf = LogisticRegression(max_iter=10000, solver='lbfgs')
clf.fit(X_train,y_train)
pred_train = clf.predict(X_train)
pred_val = clf.predict(X_val)
train_score = accuracy_score(pred_train, y_train)
val_score = accuracy_score(pred_val, y_val)
train_scores += train_score
val_scores += val_score
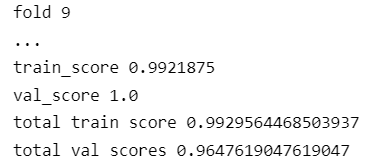
print('train_score',train_score)
print('val_score',val_score)
print("total train score",train_scores/10)
print("total val scores",val_scores/10)
- multi_class
'ovr'表示分类问题是二分类
'multinomial'表示处理多分类
’auto'根据数据的分类情况自动确定分类类型
- solver
'liblinear':坐标下降法
‘lbfgs':拟牛顿法
’newton-cg':牛顿法的一种,海森矩阵优化迭代损失函数
'sag':随机平均梯度下降
- class_weight
处理样本不平衡与参数