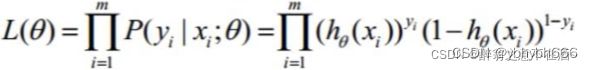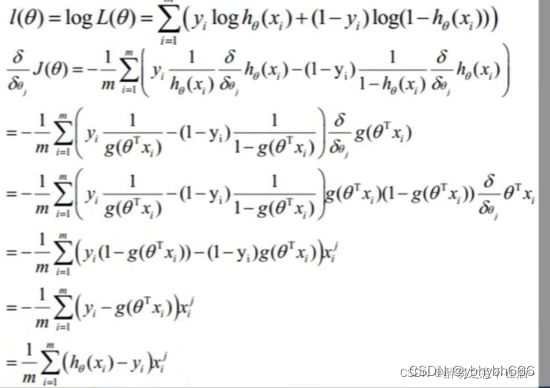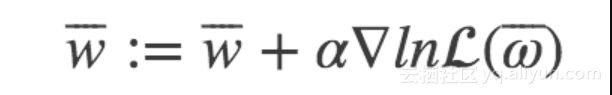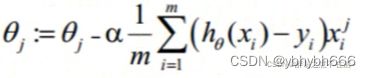python学习——逻辑回归

python学习——逻辑回归

一、逻辑回归简介

逻辑回归是分类当中极为常用的手段，它属于概率型非线性回归，分为二分类和多分类的回归模型。对于二分类的logistic回归，因变量y只有“是”和“否”两个取值，记为1和0。假设在自变量x1,x2,……,xp，作用下，y取“是”的概率是p，则取“否”的概率是1-p

1、回归步骤

1. 面对一个回归或者分类问题，建立代价函数
2. 通过优化方法迭代求解出最优的模型参数
3. 测试验证我们这个求解的模型的好坏

2、逻辑回归与多重线性回归

Logistic回归与多重线性回归实际上有很多相同之处，最大的区别就在于它们的因变量不同，其他的基本都差不多。正是因为如此，这两种回归可以归于同一个家族，即广义线性模型（generalizedlinear model）。这一家族中的模型形式基本上都差不多，不同的就是因变量不同。这一家族中的模型形式基本上都差不多，不同的就是因变量不同。

• 如果是连续的，就是多重线性回归
• 如果是二项分布，就是Logistic回归
• 如果是Poisson分布，就是Poisson回归
• 如果是负二项分布，就是负二项回归

二、sigmoid函数

在logistic回归的二分类问题中，要用到的函数就是sigmoid函数。sigmoid函数非常简单，它的表达式是：

因变量x取值范围是(-∞，+∞)，但是sigmoid函数的值域是(0, 1)。因此不管x取什么值其对应的sigmoid函数值一定会落到(0,1)范围内。它的基本图形如下：

（当z为0的时候，函数值为0.5；随着z的增大，函数值逼近于1；随着z的减小，函数值逼近于0）

解释：将任意的输入映射到[0,1]区间我们在线性回归中得到一个预测值，再将该值映射到sigmoid函数中就完成了一个值到概率的转化，也就是分类任务

其中z=

实际上g(z)并不是预测结果，而是预测结果为正例的概率，一般来说阈值为0.5，也就是当g(z)>0.5,我们就说他是正例，g(z)<0.5就是负例，但在实际应用中也可能不同。比如我们预测一个人是否患有新型冠状病毒，我们这时如果只设置阈值为0.5，那么一个人患有新冠的概率为0.45，我们的模型也会认为他没有新冠，所以这时我们不妨把阈值设置的小一些如0.1，如果概率大于0.1你就要去做检查隔离，这样可以减少误差防止漏放病人。
上述可知：
P(y=0|w,x) = 1 – g(z) #预测为负例
P(y=1|w,x) = g(z) #预测为正例

所以单条预测正确的概率为
P(正确) =*
这里解释一下，yi为某一个样本的预测值，为0或者1

那么为什么P（正确）等于这个呢，你想想，假设我们预测他为1的概率是0.8，预测他为0的概率是0.2。那么这时候如果我们说他是1，那么我们正确的概率就是0.8，如果我们说他是0，那我们正确的概率就是0.2

生成sigmoid函数图的代码：

import numpy
import math
import matplotlib.pyplot as plt
 
def sigmoid(x):
    a = []
    for item in x:
        a.append(1.0/(1.0 + math.exp(-item)))
    return a
 
x = numpy.arange(-10, 10, 0.1)
y = sigmoid(x)
plt.plot(x,y)
plt.yticks([0.0, 0.5, 1.0])
plt.axhline(y=0.5, ls='dotted', color='k')
plt.show()

sigmoid函数很适合做我们刚才提到的二分类的分类函数。假设输入数据的特征是(x0, x1, x2, …, xn)，我们在每个特征上乘以一个回归系数 (w0, w1, w2, … , wn)，然后累加得到sigmoid函数的输入z：

那么，输出就是一个在0~1之间的值，我们把输出大于0.5的数据分到1类，把输出小于0.5的数据分到0类。这就是Logistic回归的分类过程

三、极大似然估计

我们要去寻找一个w的值使得g(z)正确的概率最大，而我们在上面的推理过程中已经得到每个单条样本预测正确概率的公式，若想让预测出的结果全部正确的概率最大，根据最大似然估计，也就是所有样本预测正确的概率相乘得到的P(总体正确)最大，似然函数如下：

对其取对数可以得到：

得到的这个函数越大,证明我们得到的W就越好.此时为梯度上升求最大值，引入j(θ)=(-1/m)L(θ)转化为梯度下降任务，得到公式如下:

这就是其代价函数，也称交叉熵函数

四、求解W

当权向量 w使l(w)最大的时候,w最合理，对代价函数求导可得：

1、梯度上升法求解

梯度上升法的基本思想是：要找到某函数的最大值，最好的方法就是沿着该函数的梯度方向搜寻。如果函数为f，梯度记为D，a为步长，那么梯度上升法的迭代公式为：w：w+a*Dwf(w)。该公式停止的条件是迭代次数达到某个指定值或者算法达到某个允许的误差范围。首先对对数的函数的梯度进行计算:

通过矩阵乘法直接表示成梯度:

设步长为α, 则迭代得到的新的权重参数为:

2、梯度下降法

五、代码举例

1、自己定义函数调整参数

例子1：

数据集：学生的gre，gpa和rank信息作为变量，预测是否admit，若admit=1代表录取，admit=0代表不录取

import pandas as pd
import statsmodels.api as sm
import pylab as pl
import numpy as np
 
df = pd.read_csv("binary.csv")
 
# 浏览数据集
print (df.head())
#   admit  gre   gpa  rank
#0      0  380  3.61     3
#1      1  660  3.67     3
#2      1  800  4.00     1
#3      1  640  3.19     4
#4      0  520  2.93     4
 
# 重命名'rank'列，因为dataframe中有个方法名也为'rank'
df.columns = ["admit", "gre", "gpa", "prestige"]
 
#数据统计情况
print (df.describe())
#            admit         gre         gpa   prestige
#count  400.000000  400.000000  400.000000  400.00000
#mean     0.317500  587.700000    3.389900    2.48500
#std      0.466087  115.516536    0.380567    0.94446
#min      0.000000  220.000000    2.260000    1.00000
#25%      0.000000  520.000000    3.130000    2.00000
#50%      0.000000  580.000000    3.395000    2.00000
#75%      1.000000  660.000000    3.670000    3.00000
#max      1.000000  800.000000    4.000000    4.00000
 
# 频率表，表示prestige与admin的值相应的数量关系
print (pd.crosstab(df['admit'], df['prestige'], rownames=['admit']))
#prestige   1   2   3   4
#admit                   
#0         28  97  93  55
#1         33  54  28  12

拟变量（哑变量）

虚拟变量，也叫哑变量，可用来表示分类变量、非数量因素可能产生的影响。在计量经济学模型，需要经常考虑属性因素的影响。例如，职业、文化程度、季节等属性因素往往很难直接度量它们的大小。只能给出它们的“Yes—D=1”或”No—D=0”，或者它们的程度或等级。为了反映属性因素和提高模型的精度，必须将属性因素“量化”。通过构造0-1型的人工变量来量化属性因素。pandas提供了一系列分类变量的控制。我们可以用get_dummies来将”prestige”一列虚拟化

# 将prestige设为虚拟变量
dummy_ranks = pd.get_dummies(df['prestige'], prefix='prestige')
print (dummy_ranks.head())
#   prestige_1  prestige_2  prestige_3  prestige_4
#0           0           0           1           0
#1           0           0           1           0
#2           1           0           0           0
#3           0           0           0           1
#4           0           0           0           1

构建需要进行逻辑回归的数据框：

# 除admit、gre、gpa外，加入了上面常见的虚拟变量（注意，引入的虚拟变量列数应为虚拟变量总列数减1，减去的1列作为基准）
cols_to_keep = ['admit', 'gre', 'gpa']
data = df[cols_to_keep].join(dummy_ranks.ix[:, 'prestige_2':])
print (data.head())
#  admit  gre   gpa  prestige_2  prestige_3  prestige_4
#0      0  380  3.61           0           1           0
#1      1  660  3.67           0           1           0
#2      1  800  4.00           0           0           0
#3      1  640  3.19           0           0           1
#4      0  520  2.93           0           0           1
 
# 需要自行添加逻辑回归所需的intercept变量
data['intercept'] = 1.0

根据上述的数据框执行逻辑回归：

# 指定作为训练变量的列，不含目标列`admit`
train_cols = data[data.columns[1:]]
# sigmoid函数
def sigmoid(inX):  #sigmoid函数
    return 1.0/(1+np.exp(-inX))
#梯度上升求最优参数
def gradAscent(dataMat, labelMat): 
    dataMatrix=np.mat(dataMat) #将读取的数据转换为矩阵
    classLabels=np.mat(labelMat).transpose() #将读取的数据转换为矩阵
    m,n = np.shape(dataMatrix)
    alpha = 0.00001  #设置梯度的阀值，该值越大梯度上升幅度越大
    maxCycles = 300 #设置迭代的次数，一般看实际数据进行设定，有些可能200次就够了
    weights = np.ones((n,1)) #设置初始的参数，并都赋默认值为1。注意这里权重以矩阵形式表示三个参数。
    for k in range(maxCycles):
       h = sigmoid(dataMatrix*weights)
       error = (classLabels - h)     #求导后差值
       weights = weights + alpha * dataMatrix.transpose()* error #迭代更新权重
    return weights
 
#得到权重
weights=gradAscent(train_cols, data['admit']).getA()
#print (weights)

根据拟合出来的模型，可以进行预测：

# 在这边为方便，我们将训练集拷贝一份作为预测集（不包括 admin 列）
import copy
test_data = copy.deepcopy(data)
 
# 预测集也要添加intercept变量
test_data['intercept'] = 1.0
 
# 数据中的列要跟预测时用到的列一致
predict_cols = test_data[test_data.columns[1:]] 
 
# 进行预测，并将预测评分存入 predict 列中
predict=[]
test=np.mat(predict_cols)
for i in test:
    sum=sigmoid(i*np.mat(weights))
    print (sum)
    if sum <= 0.5:
        predict.append('0')
    else:
        predict.append('1')
test_data['predict']=predict
 
#计算预测准确率
predict_right=0
for i in range(0,400):
    if int(test_data.loc[i,'admit'])==int(test_data.loc[i,'predict']):
        predict_right=1+predict_right
    else:
        predict_right=predict_right
print ("预测准确率:")
print ("%.5f" %(predict_right/400)) 
#预测准确率:
#0.68250

由上，可知模型预测的准确率为68.25%，但往往我们会改进梯度上升方法以提高预测准确率，比如，改为随机梯度上升法。随机梯度上升法的思想是，每次只使用一个数据样本点来更新回归系数。这样就大大减小计算开销

def stocGradAscent(dataMatrix,classLabels):
    m,n=shape(dataMatrix)
    alpha=0.01
    weights=ones(n)
    for i in range(m):
        h=sigmoid(sum(dataMatrix[i] * weights))#数值计算
        error = classLabels[i]-h
        weights=weights + alpha * error * dataMatrix[i] #array 和list矩阵乘法不一样
    return weights

改进梯度上升法

def stocGradAscent1(dataMatrix,classLabels,numIter=150):
    m,n=shape(dataMatrix)
    weights=ones(n)
    for j in range(numIter):
        dataIndex=list(range(m))
        for i in range(m):
            alpha=4/(1+i+j)+0.01#保证多次迭代后新数据仍然具有一定影响力
            randIndex=int(random.uniform(0,len(dataIndex)))#减少周期波动
            h=sigmoid(sum(dataMatrix[randIndex] * weights))
            error=classLabels[randIndex]-h
            weights=weights + alpha*dataMatrix[randIndex]*error
            del(dataIndex[randIndex])
    return weights

例子2：

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']  # 显示中文
mpl.rcParams['axes.unicode_minus'] = False  # 能正确显示正负号

# 数据处理
# 加载数据
data = np.loadtxt('ex2data5.txt', delimiter=',')
# 切分
# 参数一，被切分的矩阵
# 参数二代表如何切分，[-1]代表-1之前的归为第一个返回值，其后归为第二个返回值
# 参数三，axis=0是横向切分，切分样本；axis=1是纵向切分，切分的是特征
x, y = np.split(data, [-1], axis=1)

# 特征缩放
mean = np.mean(x, 0)  # 平均数
sigma = np.std(x, 0, ddof=1)  # 标准差
x = (x-mean)/sigma  # 标准化特征缩放

# 拼接
m = len(x)
x = np.c_[np.ones((m, 1)), x]
y = np.c_[y]

# 切分训练集和测试集
num = int(m*0.7)
trainx, testx=np.split(x, [num])
trainy, testy=np.split(y, [num])

# sigmoid函数
def sigmoid(z):
    return 1.0/(1+np.exp(-z))

# 模型
def model(x, theta):
    z = x.dot(theta)
    h = sigmoid(z)   # 用sigmoid函数将连续值映射为0-1之间的概率值
    return h

# 交叉熵代价
def cost_function(h, y):
    m = len(h)
    J = -1.0/m*np.sum(y*np.log(h)+(1-y)*np.log(1-h)) 
    return J

# 梯度下降函数
def gradsDesc(x, y, alpha=0.001, count_iter=15000, lamda=0.5):
    m, n = x.shape
    theta = np.zeros((n, 1))
    jarr = np.zeros(count_iter)

    for i in range(count_iter):
        h = model(x, theta)
        e = h - y
        jarr[i] = cost_function(h, y)
        deltatheta = 1.0/m*x.T.dot(e)
        theta -= alpha*deltatheta

    return jarr, theta

# 模型精度，准确率
def accuracy(y, h):
    m = len(y)
    count = 0  #  统计预测值与真实值一致的样本个数
    for i in range(m):
        h[i] = np.where(h[i]>=0.5,1,0)  # 将预测值从概率值转换为0或1
        if h[i] == y[i]:
            count += 1

    return count/m

# 画图
def draw(x, y, theta):
    zeros = y[:,0]==0   # 选取y=0的行，其值为true
    ones = y[:,0]==1  # 选取y=1的行，其值为true

    # 画散点图
    plt.scatter(x[zeros,1],x[zeros,2],c='b',label='负向类')   # 画负向类的散点图
    plt.scatter(x[ones,1],x[ones,2], c='r', label='正向类')   # 画正向类的散点图

    # 画分界线
    # 取x1的最小值和最大值
    minx1 = x[:,1].min()
    maxx1 = x[:,1].max()

    # 计算x1的最大值和最小值在z=0上的对应的x2值
    minx1_x2 = -((theta[0]+theta[1]*minx1)/theta[2])
    maxx1_x2 = -((theta[0]+theta[1]*maxx1)/theta[2])

    # 以两个点坐标，画出z=0的决策边界
    plt.plot([minx1,maxx1], [minx1_x2, maxx1_x2])
    plt.title('测试精度:%0.2f' % (accuracy(testy, testh)))
    plt.legend()
    plt.show()

# 训练模型
jarr, theta = gradsDesc(trainx, trainy)

# 计算测试值预测值
testh = model(testx, theta)

# 计算测试集预测精度
print('测试集预测精度：', accuracy(testy, testh))
# print('测试集预测值：', testh)

#画图
draw(x, y,theta)

# 画sigmoid函数
# a = np.arange(-10, 10)
# print(a)
# b = sigmoid(a)
# plt.plot(a,b)
# plt.show()

2、sklearn库中的LogisticRegression

例子1：

import numpy as np
from sklearn.linear_model import LogisticRegression
# data数据   4,3    x1, x2, y
data = np.array([
    [1, 1, 0],
    [1, 2, 0],
    [0, 0, 1],
    [-1, 0, 1]
])

#数据集切分，  前两列特征，最后一列作为标签
x = data[:, :-1]
y = data[:, -1:]
print(x)
print(y)
[[ 1  1]
 [ 1  2]
 [ 0  0]
 [-1  0]]
[[0]
 [0]
 [1]
 [1]]

# 调用模型LogisticRegression()训练预测
model = LogisticRegression()
model.fit(x, y.ravel())  #ravel 返回连续的展平数组
y_ = model.predict(x)  #这一步的x你可以换成你想要的测试集
print(y_)
[0 0 1 1]

#打印输出的可能性， 第一列为0样本，第二列为1样本
print(model.predict_proba(x))
 [[0.67147648 0.32852352]
 [0.80685489 0.19314511]
 [0.3285313  0.6714687 ]
 [0.19314393 0.80685607]]

例子2：

# -*- coding: utf-8 -*-
"""
sklearn逻辑回归多分类例子(带模型公式提取)
"""
from sklearn.linear_model import LogisticRegression
import numpy as np
from sklearn.datasets import load_iris
#----数据加载------
 
iris = load_iris()    
X    = iris.data
y    = iris.target
#----数据归一化------
xmin   = X.min(axis=0)
xmax   = X.max(axis=0)
X_norm = (X-xmin)/(xmax-xmin)
 
#-----训练模型--------------------
clf = LogisticRegression(random_state=0,multi_class='multinomial')            
clf.fit(X_norm,y)
 
#------模型预测-------------------------------
pred_y      = clf.predict(X_norm)
pred_prob_y    = clf.predict_proba(X_norm) 
 
#------------提取系数w与阈值b-----------------------
w_norm = clf.coef_                             # 模型系数(对应归一化数据)
b_norm = clf.intercept_                           # 模型阈值(对应归一化数据)
w    = w_norm/(xmax-xmin)                       # 模型系数(对应原始数据)
b    = b_norm -  (w_norm/(xmax - xmin)).dot(xmin)      # 模型阈值(对应原始数据)
# ------------用公式预测------------------------------
wxb = X.dot(w.T)+ b
wxb = wxb - wxb.sum(axis=1).reshape((-1, 1)) # 由于担心数值过大会溢出，对wxb作调整
self_prob_y = np.exp(wxb)/np.exp(wxb).sum(axis=1).reshape((-1, 1))
self_pred_y = self_prob_y.argmax(axis=1)
 
 
#------------打印信息--------------------------
print("\n------模型参数-------")     
print( "模型系数:",w)
print( "模型阈值:",b)
print("\n-----验证准确性-------")  
print("提取公式计算的概率与sklearn自带预测概率的最大误差", abs(pred_prob_y-self_prob_y).max())

---

学习资料来源：

博主：胡萝卜酱的文章，原文链接https://blog.csdn.net/wuyy0224/article/details/122758785

博主：苟冬新的文章，原文链接：https://blog.csdn.net/weixin_40187450/article/details/89428644

博主：老饼讲解机器学习的文章，原文链接：https://blog.csdn.net/ywj_1991/article/details/123688120